一元线性回归模型实例

高一数学一元线性回归案例试题1. （2014•重庆一模）某小卖部销售一品牌饮料的零售价x （元/瓶）与销量y （瓶）的关系统计如下：已知x ，y 的关系符合线性回归方程，其中，．当单价为4.2元时，估计该小卖部销售这种品牌饮料的销量为（ ） A.20 B.22 C.24 D.26 【答案】D【解析】利用平均数公式计算平均数，，利用b=﹣20求出a ，即可得到回归直线方程，把x=4.2代入回归方程求出y 值． 解：===3.5；==40，∴a=40﹣（﹣20）×3.5=110，∴回归直线方程为：=b +a=﹣20+110， 当=4.2时，=﹣20×4.2+110=26， 故选：D ．点评：本题考查回归方程的求法，考查学生的计算能力，运算要细心．2. （2014•新余二模）已知某产品连续4个月的广告费用x i （i=1，2，3，4）千元与销售额y i （i=1，2，3，4）万元，经过对这些数据的处理，得到如下数据信息： ①x 1+x 2+x 3+x 4=18，y 1+y 2+y 3+y 4=14；②广告费用x 和销售额y 之间具有较强的线性相关关系； ③回归直线方程=bx+a 中的b=0.8（用最小二乘法求得）； 那么，当广告费用为6千元时，可预测销售额约为（ ） A ．3.5万元 B ．4.7万元 C ．4.9万元D ．6.5万元【答案】B【解析】求出数据的中心点的坐标，代入回归直线方程求得系数a ，根据广告费用为6千元，求得预报变量y 的值． 解：∵=，=， ∴数据的中心为（，）， 则=0.8×+a ，∴a=﹣，当广告费用为6千元时，可预测销售额y=0.8×6﹣0.1=4.7（万元）． 故选：B ．点评：本题考查了线性回归分析思想，考查了学生的数据处理能力，在回归分析中数据的中心在回归直线上．3. （2014•辽宁模拟）从某高中随机选取5名高三男生，其身高和体重的数据如下表所示：身高x （cm ）160165170175180）A.70.09kg B.70.12kg C.70.55kg D.71.05kg【答案】B【解析】根据所给的表格做出本组数据的样本中心点，根据样本中心点在线性回归直线上，利用待定系数法做出的值，现在方程是一个确定的方程，根据所给的x的值，代入线性回归方程，预报身高为172cm的高三男生的体重解：由表中数据可得==170，==69∵（，）一定在回归直线方程=0.56x+上故69=0.56×170+解得=﹣26.2故=0.56x﹣26.2当x=172时，=0.56×172﹣26.2="70.12"故选B．点评：本题主要考查线性回归方程的求解与运用，解题的关键是线性回归方程经过样本点的中心同时注意理解线性回归方程中相关系数的意义．4.（2014•郑州模拟）某车间加工零件的数量x与加工时间y的统计数据如表：现已求得上表数据的回归方程中的值为0.9，则据此回归模型可以预测，加工100个零件所需要的加工时间约为（）A.84分钟B.94分钟C.102分钟D.112分钟【答案】C【解析】根据表中所给的数据，做出横标和纵标的平均数，得到样本中心点，代入样本中心点求出a的值，写出线性回归方程．将x=100代入回归直线方程，得y，可以预测加工100个零件需要102分钟，这是一个预报值，不是生产100个零件的准确的时间数．解：由表中数据得：=20，=30，又值为0.9，故a=30﹣0.9×20=12，∴y=0.9x+12．将x=100代入回归直线方程，得y=0.9×100+12=102（分钟）．∴预测加工100个零件需要102分钟．故选C．点评：本题考查线性回归方程的求法和应用，解题的关键是正确应用最小二乘法求出线性回归方程的系数的运算，再一点就是代入样本中心点可以求出字母a的值，是一个中档题目．5.（2012•吉安县模拟）已知x，y的取值如表：x1234从散点图分析，y与x线性相关，且回归方程为，则a=（）A.﹣0.15B.﹣0.26C.﹣0.35D.﹣0.61【答案】A【解析】首先求出这组数据的横标和纵标的平均数，写出这组数据的样本中心点，把样本中心点代入线性回归方程求出a的值，解：∵，∴这组数据的样本中心点是（2.5，4.5），∵y与x线性相关，且，，∴4.5=1.86×2.5+a，，∴a=﹣0.15，故选A．点评：本题考查线性回归方程的求解和应用，是一个基础题6.（2012•湘潭模拟）一位母亲记录了儿子3～7岁时的身高，并根据记录数据求得身高（单位：cm）与年龄的回归模型为．若用这个模型预测这个孩子10岁时的身高，则下列叙述正确的是（）A．身高一定是145cm B．身高在145cm以上C．身高在145cm左右D．身高在145cm以下【答案】C【解析】根据回归模型为，将x=10代入即可得到预测值．解：根据回归模型为，可得x=10时，=145cm故可预测10岁时的身高在145cm左右故选C．点评：本题考查回归模型的运用，解题的关键是理解回归模型的含义，从而合理预测．7.（2011•丰台区二模）已知x，y的取值如下表：从散点图可以看出y与x线性相关，且回归方程为，则a=（）【答案】B【解析】本题考查的知识点是线性回归直线的性质，由线性回归直线方程中系数的求法，我们可知在回归直线上，满足回归直线的方程，我们根据已知表中数据计算出，再将点的坐标代入回归直线方程，即可求出对应的a值．解：∵点在回归直线上，计算得，∴回归方程过点（2，4.5）代入得4.5=0.95×2+a∴a=2.6；故选B．点评：本题就是考查回归方程过定点，考查线性回归方程，考查待定系数法求字母系数，是一个基础题8.（2010•沈阳三模）已知两个统计案例如下：①为了探究患慢性支气管炎与吸烟关系，调查了339名50岁以上的人，调查结果如表：②为了解某地母亲与女儿身高的关系，随机测得10对母女的身高如下表：则对这些数据的处理所应用的统计方法是（）A．①回归分析②取平均值B．①独立性检验②回归分析C．①回归分析②独立性检验D．①独立性检验②取平均值【答案】B【解析】本题考查的知识点是回归分析和独立性检验的概念及用法，回归分析主要判断两个定量变量之间的相关关系，而独立性检验主要用来分析两个定性变量（或称分类变量）的关系，由题目可知①中两个变量是定性变量（或称分类变量），②中两个变量是两个定量变量，分析即可得到答案．解：∵①中两个变量是定性变量（或称分类变量），②中两个变量是两个定量变量，∴对这些数据的处理所应用的统计方法是：①独立性检验②回归分析故选B点评：要判断处理数据时应采用的统计方法，关键是要分析数据中两个变量是定性变量还是定量变量，回归分析主要判断两个定量变量之间的相关关系，而独立性检验主要用来分析两个定性变量（或称分类变量）的关系．9.（2005•上海模拟）某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下：A.计算机，营销，物流B.机械，计算机，化工C.营销，贸易，建筑D.机械，营销，建筑，化工【答案】B【解析】由于用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况，根据表格的数据可以分别求出所有行业的应聘人数与招聘人数比值，然后根据这些比值即可求解．解：依题意得化工行业的应聘人数小于招聘人数，物流的应聘人数小于招聘人数，且比值化工行业大于物流机械的应聘人数大于招聘人数，故选B．点评：本题的考点是回归分析，主要考查了统计表的识别能力，解题的关键是会根据表格找出以后条件解决问题．10.实验测得四组（x，y）的值分别为（1，2），（2，3），（3，4），（4，4），则y与x间的线性回归方程是（）A．y=﹣1+x B．y=1+x C．y=1.5+0.7x D．y=1+2x【答案】C【解析】根据所给的四对数据，算出y与x的平均数，把所求的平均数代入求b的公式，算出b 的值，再把它代入求a的式子，求出a的值，写出线性回归方程即可．解：根据题意得：==2.5，==3.25，b==0.7，a=﹣b=3.25﹣0.7×2.5=1.5，∴y与x间的线性回归方程是y=1.5+0.7x．故选：C．点评：本题考查线性回归方程的求法，在一组具有相关关系的变量的数据间，利用最小二乘法做出线性回归方程的系数，再代入样本中心点求出a的值，本题是一个基础题．。

第二章 一元线性回归模型典型例题分析例1、令kids 表示一名妇女生育孩子的数目，educ 表示该妇女接受过教育的年数。

生育率对教育年数的简单回归模型为μββ++=educ kids 10（1）随机扰动项μ包含什么样的因素？它们可能与教育水平相关吗？（2）上述简单回归分析能够揭示教育对生育率在其他条件不变下的影响吗？请解释。

例2．已知回归模型μβα++=N E ，式中E 为某类公司一名新员工的起始薪金（元），N 为所受教育水平（年）。

随机扰动项μ的分布未知，其他所有假设都满足。

如果被解释变量新员工起始薪金的计量单位由元改为100元，估计的截距项与斜率项有无变化？如果解释变量所受教育水平的度量单位由年改为月，估计的截距项与斜率项有无变化？例3．对于人均存款与人均收入之间的关系式t t t Y S μβα++=使用美国36年的年度数据得如下估计模型，括号内为标准差：)011.0()105.151(067.0105.384ˆtt Y S +=＝0.538 023.199ˆ=σ （1）β的经济解释是什么？（2）α和β的符号是什么？为什么？实际的符号与你的直觉一致吗？如果有冲突的话，你可以给出可能的原因吗？（3）对于拟合优度你有什么看法吗？ （4）检验统计值？例4．下列方程哪些是正确的？哪些是错误的？为什么？⑴ y xt n t t=+=αβ12,,, ⑵ yx t n t tt=++=αβμ12,,, ⑶ y x t n t t t=++= ,,,αβμ12⑷ ,,,y x t n t t t =++=αβμ12 ⑸ y x t n t t =+= ,,,αβ12 ⑹ ,,,y x t n t t=+=αβ12 ⑺ y x t n t t t =++= ,,,αβμ12 ⑻ ,,,y x t n t t t=++=αβμ12 其中带“＾”者表示“估计值”。

例5．对于过原点回归模型i i i u X Y +=1β ，试证明∑=∧221)(iu X Var σβ例6、对没有截距项的一元回归模型i i i X Y μβ+=1称之为过原点回归（regression through the origin ）。

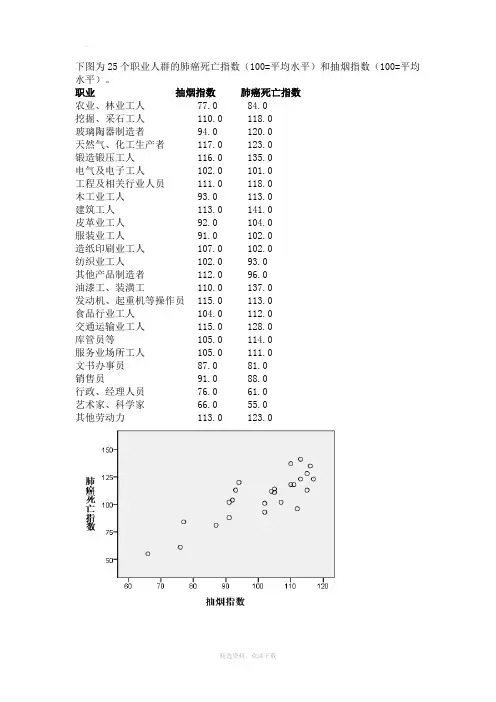
下图为25个职业人群的肺癌死亡指数（100=平均水平）和抽烟指数（100=平均水平）。

职业抽烟指数肺癌死亡指数农业、林业工人77.0 84.0挖掘、采石工人110.0 118.0玻璃陶器制造者94.0 120.0天然气、化工生产者117.0 123.0锻造锻压工人116.0 135.0电气及电子工人102.0 101.0工程及相关行业人员111.0 118.0木工业工人93.0 113.0建筑工人113.0 141.0皮革业工人92.0 104.0服装业工人91.0 102.0造纸印刷业工人107.0 102.0纺织业工人102.0 93.0其他产品制造者112.0 96.0油漆工、装潢工110.0 137.0发动机、起重机等操作员115.0 113.0食品行业工人104.0 112.0交通运输业工人115.0 128.0库管员等105.0 114.0服务业场所工人105.0 111.0文书办事员87.0 81.0销售员91.0 88.0行政、经理人员76.0 61.0艺术家、科学家66.0 55.0其他劳动力113.0 123.0散点图呈线性关系令Y=肺癌死亡指数，X=抽烟指数，做线性回归分析如下：表2中R=0.839 表示两变量高度相关R方=0.703 表示拟合较好，散点相对集中于回归线表3中sig.<0.05 则自变量与因变量具有显著的线性关系，即可以用回归模型表示表4中自变量sig.<0.05 则自变量对因变量的线性影响是显著的由此得到抽烟指数及肺癌死亡指数的一元回归方程：Y=-24.421+1.301X即抽烟指数每变动一个单位则肺癌死亡指数平均变动1.301个单位Welcome !!! 欢迎您的下载，资料仅供参考！。

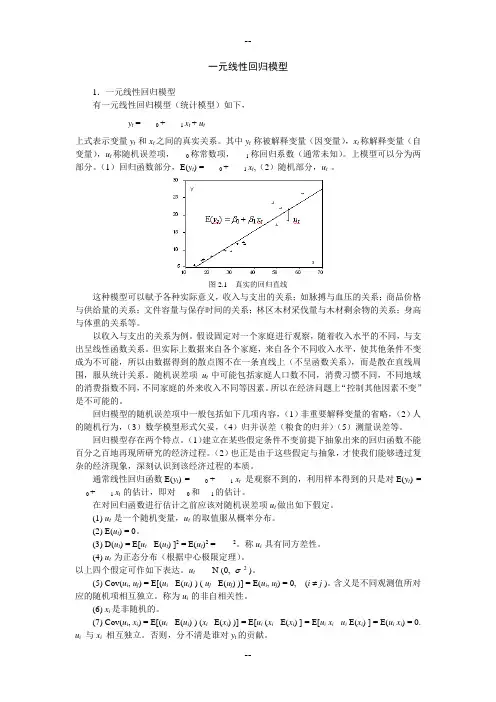
一元线性回归模型1．一元线性回归模型有一元线性回归模型（统计模型）如下，y t = 0 + 1 x t + u t上式表示变量y t 和x t之间的真实关系。

其中y t 称被解释变量（因变量），x t称解释变量（自变量），u t称随机误差项，0称常数项，1称回归系数（通常未知）。

上模型可以分为两部分。

（1）回归函数部分，E(y t) = 0 + 1 x t,（2）随机部分，u t。

图2.1 真实的回归直线这种模型可以赋予各种实际意义，收入与支出的关系；如脉搏与血压的关系；商品价格与供给量的关系；文件容量与保存时间的关系；林区木材采伐量与木材剩余物的关系；身高与体重的关系等。

以收入与支出的关系为例。

假设固定对一个家庭进行观察，随着收入水平的不同，与支出呈线性函数关系。

但实际上数据来自各个家庭，来自各个不同收入水平，使其他条件不变成为不可能，所以由数据得到的散点图不在一条直线上（不呈函数关系），而是散在直线周围，服从统计关系。

随机误差项u t中可能包括家庭人口数不同，消费习惯不同，不同地域的消费指数不同，不同家庭的外来收入不同等因素。

所以在经济问题上“控制其他因素不变”是不可能的。

回归模型的随机误差项中一般包括如下几项内容，（1）非重要解释变量的省略，（2）人的随机行为，（3）数学模型形式欠妥，（4）归并误差（粮食的归并）（5）测量误差等。

回归模型存在两个特点。

（1）建立在某些假定条件不变前提下抽象出来的回归函数不能百分之百地再现所研究的经济过程。

（2）也正是由于这些假定与抽象，才使我们能够透过复杂的经济现象，深刻认识到该经济过程的本质。

通常线性回归函数E(y t) = 0 + 1 x t是观察不到的，利用样本得到的只是对E(y t) = + 1 x t 的估计，即对0和1的估计。

在对回归函数进行估计之前应该对随机误差项u t做出如下假定。

(1) u t 是一个随机变量，u t 的取值服从概率分布。

8.5一元线性回归案例一、教学内容与教学对象分析学生将在必修课程学习统计的基础上，通过对典型案例的讨论，了解和使用一些常用的统计方法，进一步体会运用统计方法解决实际问题的基本思想，认识统计方法在决策中的作用。

二、学习目标1、知识与技能通过本节的学习，了解回归分析的基本思想，会对两个变量进行回归分析，明确建立回归模型的基本步骤，并对具体问题进行回归分析，解决实际应用问题。

2、过程与方法 本节的学习，应该让学生通过实际问题去理解回归分析的必要性，明确回归分析的基本思想，从散点图中点的分布上我们发现直接求回归直线方程存在明显的不足，从中引导学生去发现解决问题的新思路—进行回归分析，进而介绍残差分析的方法和利用R 的平方来表示解释变量对于预报变量变化的贡献率，从中选择较为合理的回归方程，最后是建立回归模型基本步骤。

3、情感、态度与价值观 通过本节课的学习，首先让显示了解回归分析的必要性和回归分析的基本思想，明确回归分析的基本方法和基本步骤，培养我们利用整体的观点和互相联系的观点，来分析问题，进一步加强数学的应用意识，培养学生学好数学、用好数学的信心。

加强与现实生活的联系，以科学的态度评价两个变量的相关系。

教学中适当地增加学生合作与交流的机会，多从实际生活中找出例子，使学生在学习的同时。

体会与他人合作的重要性，理解处理问题的方法与结论的联系，形成实事求是的严谨的治学态度和锲而不舍的求学精神。

培养学生运用所学知识，解决实际问题的能力。

三、教学重点、难点教学重点：熟练掌握回归分析的步骤；各相关指数、建立回归模型的步骤；通过探究使学生体会有些非线性模型通过变换可以转化为线性回归模型，了解在解决实际问题的过程中寻找更好的模型的方法。

教学难点：求回归系数 a , b ；相关指数的计算、残差分析；了解常用函数的图象特点，选择不同的模型建模，并通过比较相关指数对不同的模型进行比较。

四、教学策略： 教学方法：诱思探究教学法学习方法：自主探究、观察发现、合作交流、归纳总结。

一元线性回归模型案例一元线性回归模型是统计学中最基本、应用最广泛的一种回归分析方法，可以用来探究自变量与因变量之间的线性关系。

一元线性回归模型的数学公式为：y = β0 + β1x，其中y表示因变量，x表示自变量，β0和β1分别为截距和斜率。

下面以一个实际案例来说明一元线性回归模型的应用。

假设我们有一组数据，其中x表示一个房屋的面积，y表示该房屋的售价，我们想利用一元线性回归模型来预测房屋的售价。

首先，我们需要收集一组已知数据，包括房屋的面积和售价。

假设我们收集了10个不同房屋的面积和售价数据，如下所示：房屋面积（x）（平方米）售价（y）（万元）80 12090 130100 140110 150120 160130 170140 180150 190160 200170 210我们可以根据这组数据绘制散点图，横坐标表示房屋面积x，纵坐标表示售价y，如下所示：（插入散点图）接下来，我们可以利用最小二乘法来拟合一条直线，使其能够最好地拟合这些散点。

最小二乘法是一种最小化误差平方和的方法，可以得到最优的拟合直线。

根据一元线性回归模型的公式，可以通过计算拟合直线的斜率β1和截距β0来实现最小二乘法。

其中，斜率β1可以通过下式计算得到：β1 = n∑(xiyi) - (∑xi)(∑yi)n∑(xi^2) - (∑xi)^2截距β0可以通过下式计算得到：β0 = (1/n)∑yi - β1(1/n)∑xi通过带入已知数据，我们可以计算得到斜率β1和截距β0的具体值。

在本例中，计算结果如下：β1 ≈ 1.0667β0 ≈ 108.6667最后，利用得到的斜率β1和截距β0，我们可以得到一元线性回归模型的具体公式为：y ≈ 108.6667 + 1.0667x我们可以利用这个回归模型进行预测。

例如，如果有一个房屋的面积为130平方米，那么根据回归模型，可以预测该房屋的售价为170 + 108.6667 ≈ 278.6667万元。

⼀元线性回归模型案例第⼆章⼀元线性回归模型案例⼀、中国居民⼈均消费模型从总体上考察中国居民收⼊与消费⽀出的关系。

表2.1给出了1990年不变价格测算的中国⼈均国内⽣产总值（GDPP）与以居民消费价格指数（1990年为100）所见的⼈均居民消费⽀出（CONSP）两组数据。

1) 建⽴模型，并分析结果。

输出结果为：对应的模型表达式为：201.1070.3862CONSP GDPP =+(13.51) (53.47) 20.9927,2859.23,0.55R F DW ===从回归估计的结果可以看出，拟合度较好，截距项和斜率项系数均通过了t 检验。

中国⼈均消费增加10000元，GDP 增加3862元。

⼆、线性回归模型估计表2.2给出⿊龙江省伊春林区1999年16个林业局的年⽊材采伐量和相应伐⽊剩余物数据。

利⽤该数据（1）画散点图；（2）进⾏OLS 回归；（3）预测。

表2.2 年剩余物y 和年⽊材采伐量x 数据（1）画散点图先输⼊横轴变量名，再输⼊纵轴变量名得散点图（2）OLS估计弹出⽅程设定对话框得到输出结果如图：由输出结果可以看出，对应的回归表达式为：0.76290.4043t t yx =-+ (-0.625) (12.11)20.9129,146.7166, 1.48R F DW === （3）x=20条件下模型的样本外预测⽅法⾸先修改⼯作⽂件范围将⼯作⽂件范围从1—16改为1—17确定后将⼯作⽂件的范围改为包括17个观测值，然后修改样本范围将样本范围从1—16改为1—17打开x的数据⽂件，利⽤Edit+/-给x的第17个观测值赋值为20将Forecast sample选择区把预测范围从1—17改为17—17，即只预测x=20时的y的值。

由上图可以知道，当x=20时，y的预测值是7.32，yf的分布标准差是2.145。

三、表2.3列出了中国1978—2000年的参政收⼊Y和国内⽣产总值GDP的统计资料。

运用一元线性回归模型所做的预测0911554 经济系 XXX一．提出问题：对某市城镇居民年人均可支配收入X ，研究它与年人均消费性支出Y 之间的关系。

二．建立模型：消费性支出除受可支配收入的影响之外，还受到其它变量及随机因素的影响，将其它变量及随机因素的影响均归并到随机变量u 中； 根据X 与Y 的样本数据，可做二者的散点图：4005006007008009001,0001,1001,2001,300XY可知，二者变化趋势是线性的，由此建立两者之间的一元线性回归模型Y i =0β+1βX i +u i模型的假设条件：（1） 随机误差项u i 是随机变量，服从正态分布，且E(u i )=0，Var(u i )=2u σ；（2） (,)0i j Cov u u =，i≠j,即随机误差项u 无序列相关； （3） 解释变量X 与随机项u 不相关，即Cov(u i ,X i )=0。

三．估计结果：由样本观测数据（见附录1），样本回归模型为Y t =0ˆβ+1ˆβX t +e t 通过Eviews 软件估计一元线性回归模型，可得样本回归方程为ˆt Y=135.31+0.69X t （5.47）（28.04）， r 2=0.98括号内数字为回归系数对应的t 统计量的值。

（见附录2） 四．评价模型： （1）结构分析1ˆβ=0.69是样本回归方程的斜率，它表示该市城镇居民的消费倾向，说明年人均可支配收入每增加1元，将0.69元用于消费性支出；0ˆβ=135.31是样本回归方程的截距，表示不受可支配收入影响的自发消费行为。

1ˆβ和0ˆβ的符号和大小，均符合经济理论及目前该市的实际情况。

（2）拟合优度：r 2=0.98，说明总离差平方和的98%被样本回归直线解释，仅2%未被解释。

因此样本回归直线对样本点拟合优度很高。

五．预测：分别给出1999年、2000年该市人均可支配收入为X 1999=1763元，X 2000=1863元。

一元线性回归模型：案例分析下面用一个实例对本章内容作一简单回顾。

我们将收集中国财政收入和国内生产总值在1978~2006年间的历史数据，然后建立两者的一元线性回归模型，并用最小二乘法对其中的参数进行估计，最后对模型进行一些必要的检验。

一、中国财政收入和国内生产总值的历史数据由经济学等相关学科的理论我们知道，国内生产总值是财政收入的来源，因此财政收入在很大程度上由国内生产总值来决定。

为了考察中国财政收入和国内生产总值之间的关系，我们收集了中国财政收入和国内生产总值在1978~2005年间的历史数据，如表 2.4.1所示。

表2.4.1中国财政收入和国内生产总值数据表单位：亿元年份财政收入(Y) 国内生产总值(X) 年份财政收入(Y) 国内生产总值(X)1978 1132 3624 1992 3483 266521979 1146 4038 1993 4349 345611980 1160 4518 1994 5218 466701981 1176 4860 1995 6242 607941982 1212 5302 1996 7408 711771983 1367 5957 1997 8651 789731984 1643 7207 1998 9876 844021985 2005 8989 1999 11444 896771986 2122 10201 2000 13395 992151987 2199 11955 2001 16386 1096551988 2357 14922 2002 18904 1203331989 2665 16918 2003 21715 1358231990 2937 18598 2004 26396 1598781991 3149 21663 2005 31628 183868我们以X为横轴，Y为纵轴将这些数据的描绘在二维坐标图上，得到如下的散点图(图2.4.1 )。

第十三讲简单线性相关（一元线性回归分析）对于两个或更多变量之间的关系，相关分析考虑的只是变量之间是否相关、相关的程度，而回归分析关心的问题是：变量之间的因果关系如何。

回归分析是处理一个或多个自变量与因变量间线性因果关系的统计方法。

如婚姻状况与子女生育数量，相关分析可以求出两者的相关强度以及是否具有统计学意义，但不对谁决定谁作出预设，即可以相互解释，回归分析则必须预先假定谁是因谁是果，谁明确谁为因与谁为果的前提下展开进一步的分析。

一、一元线性回归模型及其对变量的要求（一）一元线性回归模型1、一元线性回归模型示例两个变量之间的真实关系一般可以用以下方程来表示：Y=A+BX+方程中的 A 、B 是待定的常数，称为模型系数，是残差，是以X预测Y 产生的误差。

两个变量之间拟合的直线是：y a bxy 是y的拟合值或预测值，它是在X 条件下 Y 条件均值的估计a 、b 是回归直线的系数，是总体真实直线距，当自变量的值为0 时，因变量的值。

A、B 的估计值， a 即 constant 是截b 称为回归系数，指在其他所有的因素不变时，每一单位自变量的变化引起的因变量的变化。

可以对回归方程进行标准化，得到标准回归方程：y x为标准回归系数，表示其他变量不变时，自变量变化一个标准差单位（ Z XjXj），因变量 Y 的标准差的平均变化。

S j由于标准化消除了原来自变量不同的测量单位，标准回归系数之间是可以比较的，绝对值的大小代表了对因变量作用的大小，反映自变量对Y 的重要性。

（二）对变量的要求：回归分析的假定条件回归分析对变量的要求是：自变量可以是随机变量，也可以是非随机变量。

自变量 X 值的测量可以认为是没有误差的，或者说误差可以忽略不计。

回归分析对于因变量有较多的要求，这些要求与其它的因素一起，构成了回归分析的基本条件：独立、线性、正态、等方差。

（三）数据要求模型中要求一个因变量，一个或多个自变量（一元时为 1 个自变量）。

一元线性回归模型案例一元线性回归是统计学中常用的一种回归分析方法，用于研究一个自变量和一个因变量之间的线性关系。

在本文中，我们将通过一个实际案例来介绍一元线性回归模型的应用和分析过程。

案例背景：假设我们是某家电商平台的数据分析师，我们希望通过用户的年龄来预测其在平台上的消费金额。

我们收集了100位用户的年龄和其在平台上的消费金额的数据，现在我们希望利用一元线性回归模型来分析这些数据，以便更好地了解用户消费行为。

数据分析：首先，我们需要对收集到的数据进行初步的分析。

我们可以使用散点图来观察年龄和消费金额之间的关系。

通过观察散点图，我们可以初步判断年龄和消费金额之间是否存在线性关系，以及线性关系的方向和强度。

模型建立：在确认了年龄和消费金额之间存在线性关系后，我们可以建立一元线性回归模型。

模型的基本形式为，Y = β0 + β1X + ε，其中Y表示因变量（消费金额），X表示自变量（年龄），β0和β1分别表示截距和斜率，ε表示误差项。

我们需要通过最小二乘法来估计β0和β1的值，从而建立回归方程。

模型评价：建立回归模型后，我们需要对模型进行评价。

我们可以通过计算回归方程的拟合优度R^2来评价模型的拟合程度，R^2的取值范围为0到1，值越接近1表示模型拟合得越好。

此外，我们还可以利用残差分析来检验模型的假设是否成立，以及检验模型的稳健性和可靠性。

预测分析：最后，我们可以利用建立的回归模型进行预测分析。

通过输入不同年龄的值，我们可以利用回归方程来预测用户在平台上的消费金额。

预测分析可以帮助电商平台更好地了解不同年龄段用户的消费特点，从而制定针对性的营销策略和服务方案。

结论：通过以上一元线性回归模型的应用分析，我们可以得出结论，用户的年龄和在平台上的消费金额之间存在一定的线性关系，通过建立回归模型，我们可以对用户的消费金额进行预测和分析。

这对于电商平台来说具有重要的参考价值，可以帮助平台更好地了解用户消费行为，从而提升用户体验和增加销售额。

一元线性回归模型案例分析一、研究的目的要求居民消费在社会经济的持续发展中有着重要的作用。

居民合理的消费模式和居民适度的消费规模有利于经济持续健康的增长，而且这也是人民生活水平的具体体现。

改革开放以来随着中国经济的快速发展，人民生活水平不断提高，居民的消费水平也不断增长。

但是在看到这个整体趋势的同时，还应看到全国各地区经济发展速度不同，居民消费水平也有明显差异。

例如，2002年全国城市居民家庭平均每人每年消费支出为6029.88元, 最低的黑龙江省仅为人均4462.08元，最高的上海市达人均10464元，上海是黑龙江的2.35倍。

为了研究全国居民消费水平及其变动的原因，需要作具体的分析。

影响各地区居民消费支出有明显差异的因素可能很多，例如，居民的收入水平、就业状况、零售物价指数、利率、居民财产、购物环境等等都可能对居民消费有影响。

为了分析什么是影响各地区居民消费支出有明显差异的最主要因素，并分析影响因素与消费水平的数量关系，可以建立相应的计量经济模型去研究。

二、模型设定我们研究的对象是各地区居民消费的差异。

居民消费可分为城市居民消费和农村居民消费，由于各地区的城市与农村人口比例及经济结构有较大差异，最具有直接对比可比性的是城市居民消费。

而且，由于各地区人口和经济总量不同，只能用“城市居民每人每年的平均消费支出”来比较，而这正是可从统计年鉴中获得数据的变量。

所以模型的被解释变量Y 选定为“城市居民每人每年的平均消费支出”。

因为研究的目的是各地区城市居民消费的差异，并不是城市居民消费在不同时间的变动，所以应选择同一时期各地区城市居民的消费支出来建立模型。

因此建立的是2002年截面数据模型。

影响各地区城市居民人均消费支出有明显差异的因素有多种，但从理论和经验分析，最主要的影响因素应是居民收入，其他因素虽然对居民消费也有影响，但有的不易取得数据，如“居民财产”和“购物环境”；有的与居民收入可能高度相关，如“就业状况”、“居民财产”；还有的因素在运用截面数据时在地区间的差异并不大，如“零售物价指数”、“利率”。