2-5 力学相对性原理 惯性系与非惯性系
- 格式:ppt
- 大小:567.00 KB
- 文档页数:6




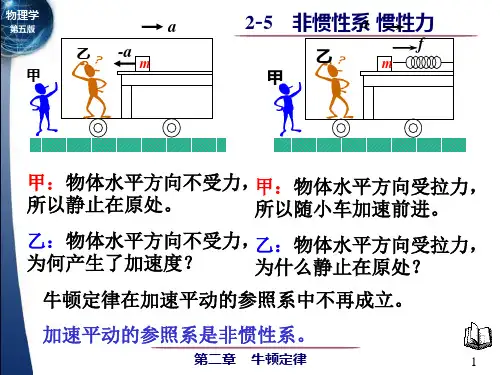
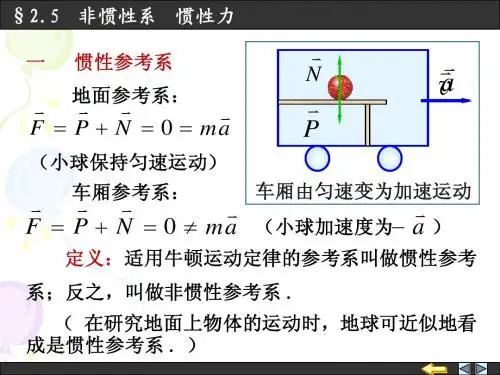

初三物理惯性系与非惯性系区分初三物理:惯性系与非惯性系区分物理学中,惯性系和非惯性系是两个重要的概念。
它们用来描述物体在运动过程中的参考系特性。
本文将详细介绍初三物理中关于惯性系和非惯性系的区分。
1. 惯性系的定义和特点惯性系是指一个参考系,在其中物体的运动状态不受任何外力作用时,将保持静止或匀速直线运动。
也就是说,如果在惯性系中观察物体,不会感受到加速度或受力的存在。
这是牛顿第一定律的基本原理。
在惯性系中,物体的运动状态可以用矢量来表示。
例如,在一维直线运动中,我们可以使用位置、速度和加速度这三个矢量来描述物体在惯性系中的运动。
2. 非惯性系的定义和特点非惯性系是指一个参考系,在其中物体的运动状态受到了外力的影响,因而具有加速度。
在非惯性系中观察物体,会感受到惯性力的存在。
惯性力是一种虚拟力,它的作用是使物体在非惯性系中仿佛在惯性系中运动,从而保持牛顿第一定律的成立。
非惯性系的一个典型例子是旋转参考系。
在旋转参考系中观察物体,会产生离心力或向心力等惯性力的效果。
比如,我们坐在旋转的摩天轮上,会感受到向外的离心力,这是因为摩天轮以一定的角速度旋转,而我们的身体有惯性继续向前运动。
3. 区分惯性系和非惯性系的方法惯性系和非惯性系可以通过以下方法进行区分:首先,可以观察物体在参考系下的运动状态。
如果物体在参考系中保持静止或匀速直线运动而不受力的作用,那么这个参考系就是惯性系。
反之,如果物体在参考系下运动状态出现加速度,那么这个参考系就是非惯性系。
其次,可以通过观察其他物体在该参考系下的运动情况来判断。
如果其他物体也表现出类似的运动状态,那么这个参考系是惯性系。
如果其他物体的运动表现出与物体自身不一致的加速度或受力情况,那么这个参考系就是非惯性系。
最后,可以通过实验来验证。
在一个参考系中进行实验观测,如果实验结果符合牛顿运动定律,那么这个参考系就是惯性系;如果实验结果出现不符合预期的情况,那么这个参考系就是非惯性系。

惯性力与非惯性系摘要惯性力是非惯性系中的非真实力,本文证明了在非惯性系中将惯性力视为真实力计入后,惯性系下的所有力学规律在非惯性系下都能成立。
当惯性力做功与路径无关时,可以引入惯性力势能,引入惯性力势能并计入系统总机械能后,机械能守恒体系中的条件与结论也仍然成立。
关键字:非惯性系; 惯性力; 惯性力势能ABSTRACTInertia force is unreal power in non-inertia system. It proves in this article that when inertia force is added as real power in non-inertia system, all the mechanical laws which apply in inertia system also do in non-inertial system. When inertia force’s doing work has nothing to do with path, potential energy can be brought in. The conditions and conclusions still apply in the system of conservation of mechanical energy when it adds potential energy to the total mechanical energy.Keywords:Non-inertial; Inertia; Inertial force potential energy1非惯性系与惯性力我们在描绘物体的运动状态时,称选作参照场的物体或物体群,为参照系。
又因为牛顿第一定律又称为惯性定律。
所以凡适用用牛顿定律的参照系都可以称作惯性参照系。
从伽俐若相对性原理中还得到:相对于惯性参照系作匀速直线运动的参照系来说,其力学过程是完全等价的。
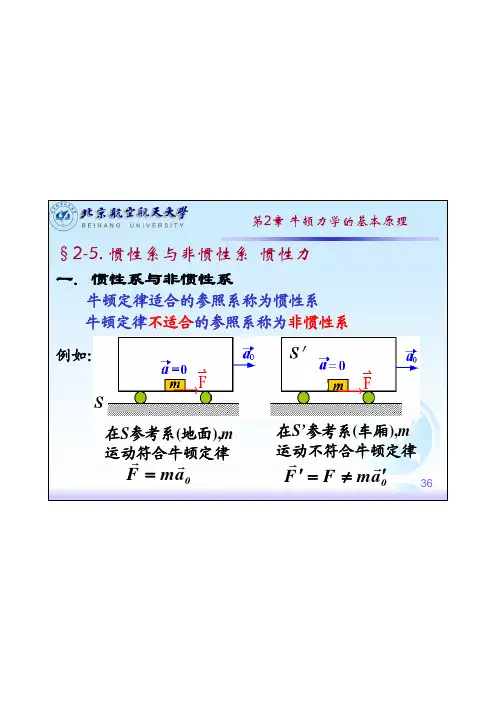
理学院 物理系 陈强第2章 牛顿力学的基本原理§2-5. 惯性系与非惯性系 惯性力 一. 惯性系与非惯性系牛顿定律适合的参照系称为惯性系 牛顿定律不适合的参照系称为非惯性系 例如:在S参考系(地面),m 运动符合牛顿定律 rr F = m a0在S’参考系(车厢),m 运动不符合牛顿定律r r ′ F ′ = F ≠ m a036理学院 物理系 陈强第2章 牛顿力学的基本原理二. 惯性力1. 平动非惯性系中的惯性力 设:非惯性系S’相对惯性系 r S 平动,加速度为: a0r r S: F = m a r r r r r r S′: F ′ = F m′ = m a′ = a − a0 ≠ a r r 故 F ′ ≠ m a ′ 牛顿第二定律在S’系中不成立 r r r r r r 由 F = ma = m( a′ + a ) = ma′ + ma 0 0 r r r 得 F − m a0 = m a ′37理学院 物理系 陈强第2章 牛顿力学的基本原理定义: 则有r r F0 = − m a 0 为惯性力(inertial force) r r r F + F0 = m a ′上式表明,在非惯性系S′ 中,只要将通常的合外力 F再加上惯性力F0,则牛顿第二定律形式上成立. 惯性力是参考系加速运动引起的附加力,本质上是 物体惯性的体现。
它不是物体间的相互作用,没有施力 物体,因而也就没有反作用力。
在非惯性系中用它分析 问题通常比较方便。
38理学院 物理系 陈强第2章 牛顿力学的基本原理2. 匀速转动非惯性系中的惯性力 设S’系相对惯性系S 匀速转动 (1) 物体m在S’中静止r r r 2 f = m a = m ω ( − r ) S: s n r S′: a ′ = 0 r r r ′=0 f + F = m a 令 s 0 r r 则 F0 = m ω 2 rr 2r F0 = m ω r ——惯性离心力(inertial centrifugal force)39理学院 物理系 陈强第2章 牛顿力学的基本原理例如:重力加速度ω2 2 g 2 = a引 + a离 − 2 a引a离 sin θθr a引r gr a离a引 >> a离 g ≈ a引 − a离 sin θg赤道=9.778 m/s2 g北极=9.832 m/s2• 在地表面用 g ,已考虑惯性离心力在内。


第二章1§2.3 力学相对性原理非惯性系中的力学定律一、力学相对性原理在经典力学中,质量、时间、空间和第二章(1)在惯性系中进行力学实验,无法确(2)力学定理在所有惯性系中具有相同(3)力学定律对惯性系变换具有不变性。
2第二章3a 非惯性系Fmaa F m ='a )'(0a a +=m第二章4Fm'a 'a F m ≠第二章5a Fm'a 惯F 惯性力惯性力是非惯性系中假想的力,是为使非惯性系中的方程和惯性系中的一致,反映了非惯性系的加速效应。
惯性力没有施力者,也没有反作用力。
成立牛顿定律惯'a F Fm =+0a F m -=惯'a m a m =-)0第二章6惯性离心力设水平光滑转台绕固定于地面的坚直轴以匀速的线连在转轴上相对静止。
转动非惯性系参照系相对惯性系只有转动时,称为转动非惯性参照系。
惯性离心力F ir m T F i练习第二章7地球为非惯性系,物体所受力有引P 的静止物体。
考虑地球自转的影响,求物体的重力和惯性力F iN Pm第二章8之ϕ重力加速度F iN F i第二章9水平方向垂直方向惯性力返回a第二章10§2.4 动量定理动量守恒定律冲量I :力的时间累积效应牛顿定律是力和效果之间的瞬时关系,m =-000d d v v m p p p t F p p t t -==⎰⎰⎰=d t t t0F I 单位牛·秒(N·s )一、质点动量定理第二章11=⎰xx tt x x m m t F I 00d v v -==⎰y y t t y y m m t F I 00d v v -==⎰z z tt z z m m t F I 00d v v -=x x x p t F I d d d ==y y y p t F I d d d ==zz z p t F I d d d == p t F I d d d ==第二章12tt t tt t t ∆=-=⎰IF F00d )(t t+冲量t ∆=F I第二章13第二章1421、是作用力与反作用力,得质点系动量的增量等于合外力的冲量微分式积分式P∆第二章15分量式方向上守恒)方向上守恒)方向上守恒))动量守恒可以只在一个方向上守恒,一个分量式成立,其它方向上以及系统总的)动量守恒的条件是整个运动过程中,任一时刻合外力都为零。
电 磁 诠 释78 惯性系与非惯性系一、经典理论中惯性系与非惯性系的概念 经典理论认为凡是牛顿运动定律适用的参照系为惯性系,牛顿运动定律不成立的参照系为非惯性系。
所有相对于惯性系做匀速直线运动的参照系都是惯性系,相对于惯性系做非匀速直线运动的参照系就不是惯性系。
在一般精度范围内,地球或静止在地面上的任一物体都可以近似看作惯性系。
同样,在地面上做匀速直线运动的物体也可以近似地看作惯性系,但在地面上做变速运动的物体就不能看作惯性系。
可以看出,经典理论是把匀速直线运动的参照系作为惯性系,非匀速直线运动的参照系作为非惯性系。
二、匀速直线运动和非匀速直线运动的统一 通过以前的论述,我们知道不管是匀速直线运动,还是非匀速直线运动,都存在实际加速度0αA 或αA 。
并且实际加速度的量值不随参照系的改变而改变。
这样,我们就可以用实际加速度把匀速直线运动和非匀速直线运动统一起来。
下面我们用实际加速度曲线说明之。
惯性系与非惯性系79图1 实际加速度曲线(惯性系曲线)物体m 在极地作匀速直线运动,其实际加速度0tan 00ααα⋅=g A0200tan )(α⋅-=rv g 00220tan )sin (αα⋅-=rc g 取极地g 0=9.8322 m/s 2,极地半径r =6.3568×106m ,光速c =3×108m/s 时,根据上式可画出极地实际加速度0αA 与速度斜角0α的关系曲线,如上图所示。
1. 当0α=0或v 0=0时,表现为相对静止。
2. 当0α=1.5215×105-或v 0=4.5644×103 m/s 时,极 地、匀速直线运动的实际加速度有最大值m ax 0αA =9.9731×电 磁 诠 释80 105- m/s 2。
3. 当0α=2.6353×105-或v 0=7.9058×103m/s 时,形成稳态运动,这时毗邻阻力f B =m 0αA ⋅=0。