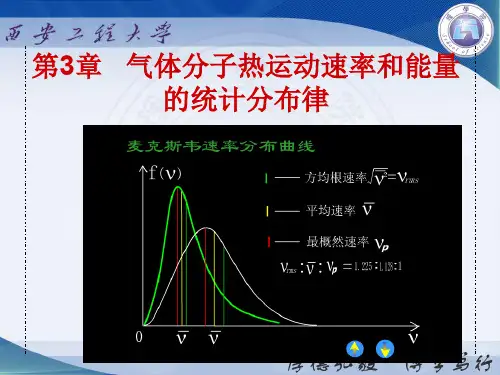
第 三 章 气体分子热运动速率和能量的统计分布律
- 格式:doc
- 大小:369.00 KB
- 文档页数:17



![热学[李椿 章立源 钱尚武]习题解答_第三章气体分子热运动速率与能量的统计分布律](https://uimg.taocdn.com/581192a543323968001c927e.webp)
第 三 章 气体分子热运动速率和能量的统计分布律3-1 设有一群粒子按速率分布如下:试求(1)平均速率V ;(2)方均根速率2V (3)最可几速率Vp解:(1)平均速率:18.32864200.5200.4800.3600.2400.12≅++++⨯+⨯+⨯+⨯+⨯=V (m/s)(2) 方均根速率37.322≅∑∑=ii i N V N V(m/s)3-2 计算300K 时,氧分子的最可几速率、平均速率和方均根速率。
解:s m RTV P /395103230031.8223=⨯⨯⨯==-μs m RTV /446103214.330031.8883=⨯⨯⨯⨯==-πμs m RTV/483103230031.83332=⨯⨯⨯==-μ3-3 计算氧分子的最可几速率,设氧气的温度为100K 、1000K 和10000K 。
解:μRTV P 2=代入数据则分别为:T=100K 时 s m V P /1028.22⨯= T=1000K 时 s m V P /1021.72⨯= T=10000K 时 s m V P /1028.23⨯=3-4 某种气体分子在温度T 1时的方均根速率等于温度T 2时的平均速率,求T 2/T 1。
解:因μRTV32=πμ28RT V =由题意得:μRT3πμ28RT =∴T 2/T 1=83π3-5 求0℃时1.0cm 3氮气中速率在500m/s 到501m/s 之间的分子数(在计算中可将dv 近似地取为△v=1m/s )解:设1.0cm 3氮气中分子数为N ,速率在500~501m/s 之间内的分子数为△N ,由麦氏速率分布律:△ N=V V e KTm N V KTm∆⋅⋅⋅-22232)2(4ππ ∵ V p2= 2KTm ,代入上式 △N=VV V ppe V V VN∆--⋅⋅222214ρπ因500到501相差很小,故在该速率区间取分子速率V =500m/s , 又s m V P /402102827331.823≅⨯⨯⨯=- △V=1m/s (vv p=)代入计算得:△N=×10-3N 个3-6 设氮气的温度为300℃,求速率在3000m/s 到3010m/s 之间的分子数△N 1与速率在1500m/s 到1510m/s 之间的分子数△N 2之比。






第 三 章 气体分子热运动速率和能量的统计分布律3-1 设有一群粒子按速率分布如下:试求(1)平均速率V ;(2)方均根速率2V (3)最可几速率Vp解:(1)平均速率:18.32864200.5200.4800.3600.2400.12≅++++⨯+⨯+⨯+⨯+⨯=V (m/s)(2) 方均根速率37.322≅∑∑=ii i N V N V(m/s)3-2 计算300K 时,氧分子的最可几速率、平均速率和方均根速率。
解:s m RTV P /395103230031.8223=⨯⨯⨯==-μs m RTV /446103214.330031.8883=⨯⨯⨯⨯==-πμs m RTV/483103230031.83332=⨯⨯⨯==-μ3-3 计算氧分子的最可几速率,设氧气的温度为100K 、1000K 和10000K 。
解:μRTV P 2=代入数据则分别为:T=100K 时 s m V P /1028.22⨯= T=1000K 时 s m V P /1021.72⨯= T=10000K 时 s m V P /1028.23⨯=3-4 某种气体分子在温度T 1时的方均根速率等于温度T 2时的平均速率,求T 2/T 1。
解:因μRTV32=πμ28RT V =由题意得:μRT3πμ28RT =∴T 2/T 1=83π3-5 求0℃时1.0cm 3氮气中速率在500m/s 到501m/s 之间的分子数(在计算中可将dv 近似地取为△v=1m/s )解:设1.0cm 3氮气中分子数为N ,速率在500~501m/s 之间内的分子数为△N ,由麦氏速率分布律:△ N=V V e KTm N V KTm∆⋅⋅⋅-22232)2(4ππ∵ V p2= 2KTm ,代入上式△N=VV V ppe V V VN∆--⋅⋅222214ρπ因500到501相差很小,故在该速率区间取分子速率V =500m/s , 又s m V P /402102827331.823≅⨯⨯⨯=- △V=1m/s (vv p =1.24)代入计算得:△N=1.86×10-3N 个3-6 设氮气的温度为300℃,求速率在3000m/s 到3010m/s 之间的分子数△N 1与速率在1500m/s 到1510m/s 之间的分子数△N 2之比。
第 三 章 气体分子热运动速率和能量的统计分布律3-1 设有一群粒子按速率分布如下:试求(1)平均速率V ;(2)方均根速率2V (3)最可几速率Vp解:(1)平均速率:18.32864200.5200.4800.3600.2400.12≅++++⨯+⨯+⨯+⨯+⨯=V (m/s)(2) 方均根速率37.322≅∑∑=ii i N V N V(m/s)3-2 计算300K 时,氧分子的最可几速率、平均速率和方均根速率。
解:s m RTV P /395103230031.8223=⨯⨯⨯==-μs m RTV /446103214.330031.8883=⨯⨯⨯⨯==-πμs m RTV/483103230031.83332=⨯⨯⨯==-μ3-3 计算氧分子的最可几速率,设氧气的温度为100K 、1000K 和10000K 。
解:μRTV P 2=代入数据则分别为:T=100K 时 s m V P /1028.22⨯= T=1000K 时 s m V P /1021.72⨯= T=10000K 时 s m V P /1028.23⨯=3-4 某种气体分子在温度T 1时的方均根速率等于温度T 2时的平均速率,求T 2/T 1。
解:因μRTV32=πμ28RT V =由题意得:μRT3πμ28RT =∴T 2/T 1=83π3-5 求0℃时1.0cm 3氮气中速率在500m/s 到501m/s 之间的分子数(在计算中可将dv 近似地取为△v=1m/s )解:设1.0cm 3氮气中分子数为N ,速率在500~501m/s 之间内的分子数为△N ,由麦氏速率分布律:△ N=V V e KTm N V KTm∆⋅⋅⋅-22232)2(4ππ ∵ V p2= 2KTm ,代入上式△N=VV V ppe V V VN∆--⋅⋅222214ρπ因500到501相差很小,故在该速率区间取分子速率V =500m/s , 又s m V P /402102827331.823≅⨯⨯⨯=- △V=1m/s (vv p =1.24)代入计算得:△N=1.86×10-3N 个3-6 设氮气的温度为300℃,求速率在3000m/s 到3010m/s 之间的分子数△N 1与速率在1500m/s 到1510m/s 之间的分子数△N 2之比。
解: 取分子速率为V 1=3000m/s V 2=1500m/s, △V 1=△V 2=10m/s由5题计算过程可得: △V 1=12212214V V V p ppe V V VN∆--⋅⋅π△N 2=22222214V V V pppe V V VN∆--⋅⋅π∴ △N/△N 2=2121)(21)(21)()(ppp V V V V p e V V e V V --⋅其中V P =331018.210257331.82⨯=⨯⨯⨯-m/s v 1v p =1.375,v 2v p=0.687∴ 969.0687.0375.122687.02375.1221≅⨯⨯=∆∆--ee N N 解法2:若考虑△V 1=△V 2=10m/s 比较大,可不用近似法,用积分法求△N 1,△N 2dN=dVV V V p PeV N22234--⋅π△N 1=⎰⎰⎰-=1221V V V V dN dN dN△N 2=⎰⎰⎰-=3443V V V V dN dN dN令X i =v iv pi=1、2、3、4利用16题结果:22)([0i ix i i V e x x erf N dN --=⎰π∴ △N 1=]2)([]2)([2122112x x i e x x erf N e x x erf N -----ππ(1)△N 2=]2)([]2)([23243344x x e x x erf N e x x erf N -----ππ(2)其中V P =s m RT/10182.223⨯=μ375.111==P V V x 379.122==P V Vx 687.033==P V V x 6722.044==PV Vx 查误差函数表得:erf(x 1)=0.9482 erf(x 2)=0.9489 erf(x 3)=0.6687 erf(x 4)=0.6722将数字代入(1)、(2)计算,再求得:703.021=∆∆N N3-7 试就下列几种情况,求气体分子数占总分子数的比率: (1) 速率在区间v p ~1.0v p 1内 (2) 速度分量v x 在区间v p ~1.0v p 1内(3) 速度分量v p 、v p 、v p 同时在区间v p ~1.0v p 1内解:设气体分子总数为N ,在三种情况下的分子数分别为△N 1、△N 2、△N 3 (1) 由麦氏速率分布律: △ N=⎰⎰⎰-=1221V V V V dN dN dN令v 2=1.01v p ,v i =v p ,p i i v v x =,则111==pv v x ,01.122==p v vx ,利用16题结果可得;2122112212)(2)(x x e x x erf e x x erf N N --+--=∆ππ 查误差函数表:erf (x 1)=0.8427 erf (x 2)=0.8468 ∴008.01=∆NN (2) 由麦氏速率分布律:x v v px dv ev NdN px221--=π∴x v v v p x v v v p dv ev Ndv ev NN px px 2122)(1)(012----⎰⎰-=∆ππ)(])(exp[1)(])(exp[12020212px p x v v p x p x v v v v d v v v v d v v N N p p ⎰⎰---=∆ππ令p x v v x =, 111==pv v x ,01.122==p v vx ∴dx edx eN N x x x x ⋅-=∆--⎰⎰2122211ππ利用误差函数:dx x xp e x erf x)(2)(20-=⎰π%21.0]8427.08468.0[21)()([21122=-=-=∆x erf x erf N N (3)令pxv v x =,由麦氏速度分布律得: z y x v v v v p dv dv dv e v N dN pzy x ⋅=++--2222331ππ833230033108.0)002.0()(][)1(211222---⨯==∆=-=∆⎰⎰NN dx e dx e N N x x x x π3-8根据麦克斯韦速率分布函数,计算足够多的点,以dN/dv 为纵坐标,v 为横坐标,作1摩尔氧气在100K 和400K 时的分子速率分布曲线。
解:由麦氏速率分布律得:22232)2(4v e KTm N dv dN v KTm-=ππ将π=3.14,N=N A =6.02×1023T=100K m=32×10-3代入上式得到常数:A=e KT m N A 23)2(4ππ KTmB 2=∴22V Ae dvdNBV ⋅=- (1) 为了避免麻烦和突出分析问题方法,我们只做如下讨论:由麦氏速率分布律我们知道,单位速率区间分布的分子数随速率的变化,必然在最可几速率处取极大值,极大值为: 令22V Ae dvdNy BV ⋅==-则 0)]2(2[222=-⋅+⋅=--BV e V V e A dvdyBV BV 得BV V P 1== 又在V=0时,y=0,V →∞时,y →0 又mKT B V P 11121==mKT B V P 22221== ∵T 1=100K <T 2=400K ∴1P V <2P V 由此作出草图3-9根据麦克斯韦速率分布律,求速率倒数的平均值v1。
解:VKT m e mKTKT m V KTm d V e m KT KT m VdVe KTm dv V f Vv KTmV KT mKTmv ππππππππ42)()2(4)2()()2(4)2(4)(1102232202230223022==⋅-⋅=-⋅⋅-===∞-∞-∞-∞⎰⎰⎰3-10一容器的器壁上开有一直径为0.20mm 的小圆孔,容器贮有100℃的水银,容器外被抽成真空,已知水银在此温度下的蒸汽压为0.28mmHg 。
(1) 求容器内水银蒸汽分子的平均速率。
(2) 每小时有多少克水银从小孔逸出?解:(1))/(1098.11020114.337331.88823s m RTV ⨯=⨯⨯⨯⨯==-πμ(2)逸出分子数就是与小孔处应相碰的分子数,所以每小时从小孔逸出的分子数为:t s V n N ⋅⋅=41其中KT V P V n ⋅=4141是每秒和器壁单位面积碰撞的分子数,2)2(ds π=是小孔面积,t=3600s ,故t s V KTPN ⋅⋅⋅=41,代入数据得: N=4.05×1019(个) ∴)(1035.11005.41002.610201219233g N N mN M A--⨯=⨯⨯⨯⨯===μ3-11如图3-11,一容器被一隔板分成两部分,其中气体的压强,分子数密度分别为p 1、n 1、p 2、n 2。
两部分气体的温度相同,都等于T 。
摩尔质量也相同,均为μ。
试证明:如隔板上有一面积为A 的小孔,则每秒通过小孔的气体质量为:)(221P P A RTM -=πμ证明:设p 1>p 2,通过小孔的分子数相当于和面积为A 的器壁碰撞的分子数。
从1跑到2的分子数:t A V n N ⋅⋅=11141从2跑到1的分子数:t A V n N ⋅⋅=22241实际通过小孔的分子数:(从1转移到2))221121(41V n V n At N N N -=-=∆因t=1秒,KTPn =,πμRTV 8=T 1=T 2=T∴)(2)(841)(841212121P P A RTP P RTRTA KT P KT PRT Am n m M -=-=-==∆=πμπμμπμ若P 2>P 1,则M <0,表示分子实际是从2向1转移。
3-12 有N 个粒子,其速率分布函数为)0()(0〉〉==v v C NdvdNv f)(0)(0v v v f 〈=(1)作速率分布曲线。
(2)由N 和v 0求常数C 。
(3)求粒子的平均速率。
解:(1) )0()(0〉〉=v v C v f )(0)(0v v v f 〈= 得速率分布曲线如图示(2)∵1)(0=⎰∞dv v f∴10)(00==⎰⎰∞v cdv dv v f 即10=cv 01v c =(3)02002121)(v cv dv v vf v ===⎰∞3-13 N 个假想的气体分子,其速率分布如图3-13所示(当v >v 0时,粒子数为零)。