热学气体分子热运动速率和能量分布

热力学中的气体分子速率分布函数热力学是研究热现象和能量转换的学科，它和物理学和化学有着紧密的关系。

其中一个重要的概念就是气体分子速率分布函数，它可以用来描述气体内分子的速率分布规律。

什么是气体分子速率分布函数？在热力学中，我们通常将气体看作是一群由许多微观分子组成的粒子集合。

这些分子运动着，它们的速率不同，而气体分子速率分布函数就可以用来描述这些速率的分布规律。

在理想气体模型中，我们可以假设每个分子是一个质点，它们遵循牛顿力学定律，相互之间的碰撞完全弹性。

这样的假设很大程度上简化了问题，使得我们可以利用数学模型来描述气体的性质。

气体分子速率分布函数的表达式现在我们来看看气体分子速率分布函数的具体表达式。

在理想气体模型中，气体分子的速率可以表达为分子速率分布函数 f(v)：f(v) = 4π(v^2/n)^(3/2) * e ^ (-mv^2/2kT)其中，v 表示分子的速率，n 表示分子数，m 表示分子的质量，k 是玻尔兹曼常数，T 是气体的温度。

这个公式告诉我们有多少分子从速率为 v 的状态转化为另一个速率状态。

从这个公式里，我们可以看到，分子速率分布函数和分子的质量、温度有关。

对于一个特定的气体，当温度增加时，分子的速率分布函数也会随之变化。

如果温度越高，气体分子速率分布函数就会越宽，分子的速率也就越高。

与分子速率分布函数相关的物理量在热力学中，与气体分子速率分布函数相关的物理量还有很多。

例如，我们可以通过分子速率分布函数来计算气体的热容、内能、休耳费函数等。

这些物理量的计算需要使用复杂的数学方法和理论模型，但了解速率分布函数的基本概念是理解这些物理量的关键。

总结热力学中的气体分子速率分布函数是非常重要的一个概念，它可以用来描述气体内分子的速率分布规律。

通过对分子速率分布函数的研究，人们可以更好地理解气体的性质和物理行为。

同时，这个概念也为计算和预测气体的热力学量和热力学过程提供了基础。

分子运动与热能热能是物体分子运动所具有的能量。

分子运动是指物质微观粒子——分子的热运动。

分子运动的特性和规律对理解热现象和热能转化至关重要。

本文将以分子运动的角度来探讨和解释热能的产生和传递。

一、分子运动的基本特性1. 分子运动的速度：根据气体动理论，分子速度与温度成正比。

在给定温度下，分子的速度服从马克思韦尔分布，即速度分布为高斯分布。

2. 分子运动的路径：分子在运动中呈现随机运动、无规则碰撞的特性。

分子路径的无序性导致能量在物质中的传递和分布。

3. 分子碰撞：分子通过相互碰撞来传递能量。

在碰撞过程中，能量可以从速度更高的分子传递给速度较低的分子，实现能量的平衡。

4. 分子自由度：分子在空间中具有多种运动方式，如平动、转动和振动。

不同自由度的运动会影响分子的能量和热量的传递。

二、分子运动与热能传递1. 热平衡与热传导：当两个物体处于热平衡时，它们之间的热能不再传递。

而热传导是指物体间由于温度差异造成的热能传递。

2. 分子碰撞与热能传递：热能通过分子间的碰撞进行传递。

当两个物体温度不同，分子速度不同，碰撞会使能量从高温物体传递到低温物体。

这种能量传递方式称为热传导。

3. 物质热传导性质：物质的热传导性质与分子运动密切相关。

导热性能好的物质，其分子间的碰撞频率高，能量传递迅速，导热系数较大。

4. 热容与分子运动：物体的热容与其分子的平动能量和振动能量有关。

热容越大，物体吸收或释放的热能越大，热传递能力越强。

三、热力学定律解释1. 热力学第一定律：热力学第一定律给出了能量守恒的原则。

根据这一定律，物体的内能变化等于吸收的热量减去对外界做功的量，即ΔU = Q - W。

2. 热力学第二定律：热力学第二定律阐述了热量自然传递的方向。

根据这一定律，热量不会自动从低温物体传递到高温物体，而是从高温物体传递到低温物体，熵增加。

3. 熵与分子运动：熵是物体无序程度的度量，与分子的运动状态有关。

当物体的熵增加时，分子的运动方式更随机，热能更分散。

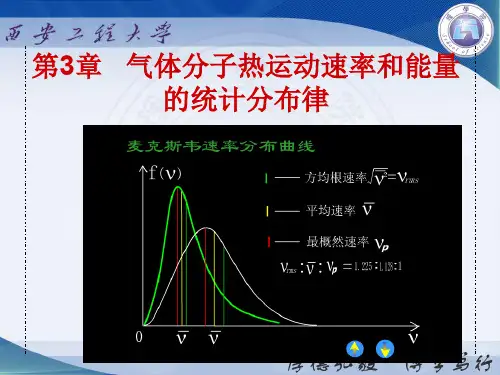
第 三 章 气体分子热运动速率和能量的统计分布律3-1 设有一群粒子按速率分布如下：试求(1)平均速率V ；（2）方均根速率2V （3）最可几速率Vp解：（1）平均速率：18.32864200.5200.4800.3600.2400.12≅++++⨯+⨯+⨯+⨯+⨯=V (m/s)(2) 方均根速率37.322≅∑∑=ii i N V N V(m/s)3-2 计算300K 时，氧分子的最可几速率、平均速率和方均根速率。

解：s m RTV P /395103230031.8223=⨯⨯⨯==-μs m RTV /446103214.330031.8883=⨯⨯⨯⨯==-πμs m RTV/483103230031.83332=⨯⨯⨯==-μ3-3 计算氧分子的最可几速率，设氧气的温度为100K 、1000K 和10000K 。

解：μRTV P 2=代入数据则分别为：T=100K 时 s m V P /1028.22⨯= T=1000K 时 s m V P /1021.72⨯= T=10000K 时 s m V P /1028.23⨯=3-4 某种气体分子在温度T 1时的方均根速率等于温度T 2时的平均速率，求T 2/T 1。

解：因μRTV32=πμ28RT V =由题意得：μRT3πμ28RT =∴T 2/T 1=83π3-5 求0℃时1.0cm 3氮气中速率在500m/s 到501m/s 之间的分子数（在计算中可将dv 近似地取为△v=1m/s ）解：设1.0cm 3氮气中分子数为N ，速率在500~501m/s 之间内的分子数为△N ，由麦氏速率分布律：△ N=V V e KTm N V KTm∆⋅⋅⋅-22232)2(4ππ ∵ V p2= 2KTm ，代入上式 △N=VV V ppe V V VN∆--⋅⋅222214ρπ因500到501相差很小，故在该速率区间取分子速率V =500m/s ， 又s m V P /402102827331.823≅⨯⨯⨯=- △V=1m/s （vv p=）代入计算得：△N=×10－3N 个3-6 设氮气的温度为300℃，求速率在3000m/s 到3010m/s 之间的分子数△N 1与速率在1500m/s 到1510m/s 之间的分子数△N 2之比。

气体分子的热运动与速度分布在我们的生活中，气体无处不在，无论是我们呼吸的空气，还是我们家中使用的燃气，都是由气体组成的。

那么，气体分子是如何运动的呢？它们的速度分布又是怎样的呢？让我们一起来探索气体分子的热运动和速度分布。

首先，让我们来了解一下气体分子的热运动。

气体分子无线自由运动着，距离彼此远去，而且它们之间的相互作用力较小。

这使得气体分子可以在容器中快速移动，并不断与容器壁碰撞。

这种热运动使得气体分子呈现出多种不同的运动方式，如直线运动、旋转运动和振动运动等。

可以说，气体分子的热运动是密不可分的。

接下来，我们来讨论气体分子的速度分布。

根据统计力学的理论推导，气体分子的速度分布服从麦克斯韦速度分布定律。

麦克斯韦速度分布定律告诉我们，在给定温度下，气体分子的速度可以呈现出一个特定的分布情况。

根据麦克斯韦速度分布定律，气体分子的速度分布呈现出高斯分布曲线。

也就是说，在给定温度下，大部分气体分子的速度集中在一个平均速度附近，而少部分气体分子的速度偏离平均速度。

这个平均速度可以由麦克斯韦-波尔兹曼速度分布定律计算得到。

麦克斯韦-波尔兹曼速度分布定律告诉我们，气体分子的平均速度与温度成正比。

具体地说，平均速度与平方根温度成正比，即$v_{avg} \propto \sqrt{T}$。

这意味着，温度越高，气体分子的平均速度也越高。

除了平均速度，气体分子的速度分布还涉及到速度的分散程度。

可以使用速度的标准差来度量速度的分散程度。

根据麦克斯韦速度分布定律，气体分子的速度标准差与平均速度成正比，即$\sigma \propto v_{avg}$。

这意味着，平均速度越高，气体分子的速度分散程度也越大。

此外，气体分子速度的分布还与气体分子的质量有关。

根据麦克斯韦-波尔兹曼速度分布定律，质量较大的分子相对运动较慢，质量较小的分子相对运动较快。

因此，在相同温度下，质量较大的气体分子的平均速度要比质量较小的分子的平均速度小。

气体的分子速率与动能分布计算气体的分子速率与动能分布计算是研究气体分子在给定温度下的运动特性的重要方法。

通过计算分子速率和动能分布，可以揭示气体分子的速度分布情况、动能转移和分子碰撞等基本动力学过程。

本文将介绍气体的分子速率与动能分布计算的基本原理和方法，并给出相关公式和计算实例。

【概述】气体分子速率与动能分布计算是通过统计力学和热力学理论推导而来的，主要基于以下假设和原理：1. 气体分子是质点：气体分子在宏观尺度上可以看作质点，忽略其内部结构和形状。

2. 分子间相互作用：气体分子之间的相互作用主要通过碰撞传递能量和动量，对于稀薄气体来说，分子间的相互作用可以被视为弹性碰撞。

3. 热力学平衡：气体分子达到热力学平衡状态，分子速率和动能分布保持一定的统计规律。

【分子速率的计算】在给定温度下，气体分子的速率服从麦克斯韦-波尔兹曼分布。

麦克斯韦-波尔兹曼速率分布函数表示了不同速率下分子的数量分布。

分子速率的计算公式为：f(v) = 4π(μ/2πkT)^(3/2)v^2e^(-μv^2/(2kT))其中，f(v)表示速率为v的分子数量，μ为分子的摩尔质量，T为温度，k为玻尔兹曼常数。

通过计算分子速率分布函数，可以得到不同速率区间内分子数量的分布情况。

这对于研究气体分子的能量转移、速率相关物性和反应动力学等问题具有重要意义。

【动能分布的计算】气体分子的动能分布可以通过速率分布函数进一步计算得到。

动能分布表示了不同分子速率下的动能分布情况。

动能分布的计算公式为：g(E) = (2πμ/(kT))^(3/2)(2/3)√(E/πμ)^(1/2)e^(-E/(kT))其中，g(E)表示动能为E的分子数量，μ为分子的摩尔质量，T为温度，k为玻尔兹曼常数。

通过计算动能分布函数，可以得到不同动能区间内分子数量的分布情况。

这对于研究气体的能量转移和反应动力学过程具有重要意义。

【计算实例】以氢气(H2)分子在300K温度下为例，计算其分子速率和动能分布。

第 三 章 气体分子热运动速率和能量的统计分布律3-1 设有一群粒子按速率分布如下：试求(1)平均速率V ；（2）方均根速率2V （3）最可几速率Vp解：（1）平均速率：18.32864200.5200.4800.3600.2400.12≅++++⨯+⨯+⨯+⨯+⨯=V (m/s)(2) 方均根速率37.322≅∑∑=ii i N V N V(m/s)3-2 计算300K 时，氧分子的最可几速率、平均速率和方均根速率。

解：s m RTV P /395103230031.8223=⨯⨯⨯==-μs m RTV /446103214.330031.8883=⨯⨯⨯⨯==-πμs m RTV/483103230031.83332=⨯⨯⨯==-μ3-3 计算氧分子的最可几速率，设氧气的温度为100K 、1000K 和10000K 。

解：μRTV P 2=代入数据则分别为：T=100K 时 s m V P /1028.22⨯= T=1000K 时 s m V P /1021.72⨯= T=10000K 时 s m V P /1028.23⨯=3-4 某种气体分子在温度T 1时的方均根速率等于温度T 2时的平均速率，求T 2/T 1。

解：因μRTV32=πμ28RT V =由题意得：μRT3πμ28RT =∴T 2/T 1=83π3-5 求0℃时1.0cm 3氮气中速率在500m/s 到501m/s 之间的分子数（在计算中可将dv 近似地取为△v=1m/s ）解：设1.0cm 3氮气中分子数为N ，速率在500~501m/s 之间内的分子数为△N ，由麦氏速率分布律：△ N=V V e KTm N V KTm∆⋅⋅⋅-22232)2(4ππ∵ V p2= 2KTm ，代入上式△N=VV V ppe V V VN∆--⋅⋅222214ρπ因500到501相差很小，故在该速率区间取分子速率V =500m/s ， 又s m V P /402102827331.823≅⨯⨯⨯=- △V=1m/s （vv p =1.24）代入计算得：△N=1.86×10－3N 个3-6 设氮气的温度为300℃，求速率在3000m/s 到3010m/s 之间的分子数△N 1与速率在1500m/s 到1510m/s 之间的分子数△N 2之比。