下载文档原格式
第 三 章 气体分子热运动速率和能量的统计分布律3-1 设有一群粒子按速率分布如下：试求(1)平均速率V ；（2）方均根速率2V （3）最可几速率Vp解：（1）平均速率：18.32864200.5200.4800.3600.2400.12≅++++⨯+⨯+⨯+⨯+⨯=V (m/s)(2) 方均根速率37.322≅∑∑=ii i N V N V(m/s)3-2 计算300K 时，氧分子的最可几速率、平均速率和方均根速率。
解：s m RTV P /395103230031.8223=⨯⨯⨯==-μs m RTV /446103214.330031.8883=⨯⨯⨯⨯==-πμs m RTV/483103230031.83332=⨯⨯⨯==-μ3-3 计算氧分子的最可几速率，设氧气的温度为100K 、1000K 和10000K 。
解：μRTV P 2=代入数据则分别为：T=100K 时 s m V P /1028.22⨯= T=1000K 时 s m V P /1021.72⨯= T=10000K 时 s m V P /1028.23⨯=3-4 某种气体分子在温度T 1时的方均根速率等于温度T 2时的平均速率，求T 2/T 1。
解：因μRTV32=πμ28RT V =由题意得：μRT3πμ28RT =∴T 2/T 1=83π3-5 求0℃时1.0cm 3氮气中速率在500m/s 到501m/s 之间的分子数（在计算中可将dv 近似地取为△v=1m/s ）解：设1.0cm 3氮气中分子数为N ，速率在500~501m/s 之间内的分子数为△N ，由麦氏速率分布律：△ N=V V e KTm N V KTm∆⋅⋅⋅-22232)2(4ππ ∵ V p2= 2KTm ，代入上式 △N=VV V ppe V V VN∆--⋅⋅222214ρπ因500到501相差很小，故在该速率区间取分子速率V =500m/s ， 又s m V P /402102827331.823≅⨯⨯⨯=- △V=1m/s （vv p=）代入计算得：△N=×10－3N 个3-6 设氮气的温度为300℃，求速率在3000m/s 到3010m/s 之间的分子数△N 1与速率在1500m/s 到1510m/s 之间的分子数△N 2之比。
第三章气体分子热运动速率和能量的统计分布⏹3.1气体分子的速率分布律⏹3.2用分子射线实验验证麦克斯韦速度分布律⏹3.3玻尔兹曼分布律重力场中微粒按高度的分布⏹3.4能量按自由度均分定理3.1气体分子的速率分布律统计规律性：分子运动论从物质微观结构出发，研究大量分子组成的系统的热性质。
其中个别分子的运动（在动力学支配下）是无规则的，存在着极大的偶然性。
但是，总体上却存在着确定的规律性。
（例：理想气体压强）人们把这种支配大量粒子综合性质和集体行为的规律性称为统计规律性。
气体中个别分子的速度具有怎样的数值和方向完全是偶然的，但就大量分子的整体来看，在一定的条件下，气体分子的速度分布也遵从一定的统计规律。
为研究气体分子速度分布的定量规律，有必要介绍分布函数的概念。
例1：统计某城市中每个商店里职工的分布情况，可用下列方法。
分布函数和平均值偶然事件：大量出现不可预测的事件。
多次重复观察同样的事件，可获得该偶然事件的分布，从而得到其统计规律。
表示该城市中的商店总数表示该城市中有个职工的商店数，称分布数。
i N i ∑=i N N 名职工的商店的百分数表示有i N N f i i 归一化的分布数,,=条件归一化,1)(==∑∑N N f i i例:我们以人的身高为例，来引入分布函数的概念。
设N 为总人数，d N （h ）为身高在h--h+d h 间的人数。
显然⎰=Nh N )(d 令f （h ）=d N （h ）/N d h ，则⎰=1d )(h h f 我们把f （h ）称为归一化分布函数。
f （h ）表征在单位高度内，身高为h 的人数占总人数的比率。
f(h)dh ：高度在h 与h+dh 之间的概率N 个人的平均身高为hf（h）h h+dhof(h)为归一化分布函数分布曲线高度在h与h+dh之间的人数：dhhNfhdN)()(=⎰=⎰=⎰=hhhfhNhhhNfNhNhd)(d)()(d推广至任一变量（物理量）x ,由分布函数f(x)求平均值，有：⎰⎰⎰===xxxfNxxNxfNNxx d)(d)(d对具有统计性的系统来讲，总存在着确定的分布函数f（x），因此，写出分布函数f（x）是研究一个系统的关键之处，具有普遍的意义。
速率分布函数一定量的气体分子总数为NdN v表示速率分布在某区间v~v+dv内的分子数，dN v/N表示分布在此区间内的分子数占总分子数的比率（或百分比）。
dN v/N是v的函数，在不同速率附近取相等的区间，此比率一般不相等。
当速率区间足够小时（宏观小，微观大），dN v/N还应与区间大小成正比。
因此有()dv v f N dN v =物理意义：速率在v 附近，单位速率区间的分子数占总分子数的比率。
f(v):速率分布函数()100==⎰⎰∞dv v f NdN Nv 归一化条件(Normalizing condition )()dvN dN v f ⋅=或麦克斯韦速率分布律(Maxwell speed distribution law )（一定条件下，速率分布函数的具体形式）在平衡态下，当气体分子间的相互作用可以忽略时，分布在任一速率区间v~v+dv 的分子数占总分子数的比率为dv v e kT m N dN kT m v v 2223224-⎪⎭⎫ ⎝⎛ππ=()2223224v e kT m v f kT m v -⎪⎭⎫ ⎝⎛ππ=麦克斯韦速率分布函数麦克斯韦速率分布曲线p v )(v f v O)(v f v麦克斯韦速率分布曲线1v 2v )(v f vO)(v f 面积NNv v f d d )(=面积NN v v f v v ∆=⎰21d )(v dv速率在区间内的分子数占总分子数的比例；或分子速率位于区间内的几率。
),(v v ),(21v v 速率在区间内的分子数占总分子数的比例；或分子速率位于区间内的几率。
),(v v v d +),(v v v d +vvnf d)()1(VNnvNNvf==,dd)(vvnf d)(∴VNd=表示单位体积内分布在速率区间内的分子数。
vvv d+→说明下式的物理意义：为分子数密度，为速率分布函数，nvf)(vvNf d)()2(vNNvfdd)(=Nd=vvNf d)(∴表示分布在速率区间内的分子数。
vvv d+→说明下式的物理意义：为分子数密度，为速率分布函数，nvf)(⎰21d)()3(vvvvfnVNnvNNvf==,dd)(vvfn vvd)(21⎰∴VNNNVN∆=∆=表示分布在单位体积内，速率区间内的分子数。
21vv→说明下式的物理意义：为分子数密度，为速率分布函数，nvf)(说明下式的物理意义：为分子数密度，为速率分布函数，nvf)(⎰⎰2121d)(d)()4(vvvvvvfvvvfvN d=NNNNvNN∆=⎰21d表示速率在区间内的分子的平均速率。
)(21vv，Nvfd)(NvdNNN∆=⎰212232224)(ve kT m vf kT mv -⎪⎭⎫⎝⎛=ππ气体的三种统计速率速率分布函数中的极大值对应的分子速率。
p v )(v f 0d )(d =vv f 极值条件(1)最可几速率:μμRTRT41.12≈=mkTp v 2=温度超高，v p 越大；分子的质量越大，v p 越小)(v f vv O最可几速率（most probable speed ）∆对大量分子而言，在相同的速率间隔中，气体分子的速率在vp附近的分子数最多。
∆对单个分子而言，速率在v p附近的几率最大。
最可几速率“vp”的意义是：气体分子速率的算术平均值。
NNvvN⎰=0dvNNv fdd)(=mkTvπ8=mkTvπ8=(2)平均速率：⎰∞=d)(vvvf2232224)(vekTmvf kTmv-⎪⎭⎫⎝⎛=ππμπμRTRT60.18≈=)(v f vvO平均速率(average speed)(3)方均根速率（root-mean-square speed）：气体分子速率平方的平均值的平方根。
μμRTRTmkTv73.1332≈==NNvvN⎰=022d⎰∞=2d v)v(fvmkT3=vNN)v(fdd=2232224)(vekTmvf kT mv-⎪⎭⎫⎝⎛=ππ2v)(v f vO方均根速率三种速率均与,成反比，但三者有一个确定的比例关系;三种速率使用于不同的场合。
讨论速率分布时用最可几速率；计算分子运动的平均距离时用平均速率；计算分子平均平动能时用方均根速率。
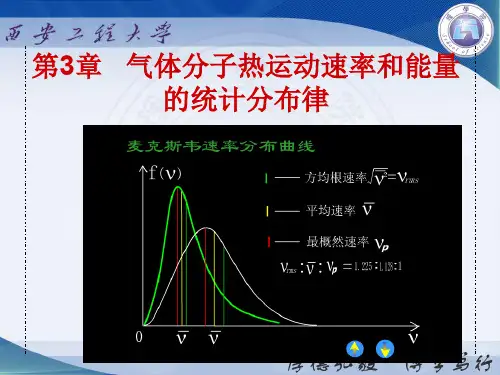
mT 2)(v f vv vO三种速率比较2vv v p <<)(v f vOv v v )(1p v f )(2p v f )(3p v f 3T 2T 1T 321T T T <<温度越高，速率大的分子数越多同一气体不同温度下速率分布比较321m m m >>)(v f vO3m 2m 1m 同一温度下不同种气体速率分布比较分子质量越小，速率大的分子数越多。
例题1试计算气体分子热运动速率的大小介于vp-v p/100和v p+v p/100之间的分子数占总分子数的百分数。
pppvvvv10099100＝-=50100100pppppvvvvvv=⎪⎭⎫⎝⎛--⎪⎭⎫⎝⎛+=∆在此利用vp，引入W=v/vp，把麦克斯韦速率分布律改写成如下简单形式：WeWWWfNN W∆π∆∆224)(-=＝解:按题意%66.15011009942100992=⎪⎭⎫⎝⎛⎪⎭⎫⎝⎛-eNNπ∆＝把这些量值代入，即得10099＝pvvW=501＝pvvW∆=∆现在例2. 有N个粒子，其速率分布函数为求：（1）速率分布曲线（2）由v 0 求常数C （3）粒子的平均速率)(CNdvdNvf==)(=vf)(0>>vv)(0vv>解（1）速率分布曲线（见下图）)(vfC（2）常数C 由归一化条件求得1)(=⎰v dvvf1=⎰v Cdv1=vC1vC=（3）平均速率：⎰=∞)(dvvvfv212vv⋅=dvvvv⎰=0121v=例3. 由麦氏分布律导出理想气体分子按平动动能的分布律,并找出最可几动能是什么？一个分子的平均平动动能是什么？解：一个分子的平动动能：221mv =εmvdvd =ε由麦氏分布律：dvv ekTmdv v f N dN kT mv⋅⋅⋅ππ==-22232)2(4)(vε⋅ε⋅ππ=ε-d e kTkT2123)1(2vdvmd e mkTmkTε⋅⋅εππ=ε-2)2(423εεd f )(2最可几动能：0)( =εεd df 令kTp 21 =ε解得221(p mv 注意：不是))2(21kT m kT m ==分子的平均平动动能为：=ε⎰∞0)(εεεd f 理论与实验符合得很好。
kT 23=ε⋅ε⋅⎰ππ=ε-∞d ekTkT 23023)1(2kTt 23=ε从理论上已经得到过：在平衡态下，当气体分子之间的相互作用可忽略时，速度分量v x 在区间v x ~v x +dv x ，v y 在区间v y ~v y +dv y ，v z 在区间v z ~v z +dv z 内的分子数占总分子数的比率为麦克斯韦速度分布律（Maxwell velocity distribution law ）上面讨论的是气体分子按速率分布的规律，对分子速度的方向未作任何确定。
下面进一步介绍气体分子按速度分布的规律。
、、()z y x kT v v v m v v v dv dv dv e kT m NdN z y x zy x 2232222++-⎪⎭⎫ ⎝⎛π=()()kTv v v m z y x z y x ekT m v ,v ,v f 2232222++-⎪⎭⎫ ⎝⎛π=麦克斯韦速度分布函数（Maxwell velocity distribution law ）＊速度空间(velocity space)的概念表示分子的速度以其分量vx、vy、vz为轴可构成一直角坐标系，由此坐标系所确定的空间为速度空间。
＊麦克斯韦速度分布律指明了分子代表点在速度空间体积元d =dvxdv y dv z中的分布情况。
＊可由麦氏速度分布律推出麦氏速率分布律。
v由图（b ）可得：dv v d 24πω=2222zy x vv v v ++=()dv v em dv dv dv e kT m N dN kT mv z y x kTv v v m z y x 2223223222242-++-⎪⎫ ⎛=⎪⎭⎫ ⎝⎛=∴πππ由麦克斯韦速度分布函数可推出速度的三个分量的分布函数。
将分布函数先后对vy和vz积分，即可求出速度分量vx在区间vx~ vx＋d vx内的分子数占总分子数N的比率：⎰⎰∞+∞-∞+∞----⎪⎭⎫⎝⎛=zkTmvykTmvxkTmvv dvedvedvekTmNdNzyxx222232222π2122222⎪⎭⎫⎝⎛==⎰⎰∞+∞-∞+∞---mkTdvedvezkTmvykTmvzyπkTmvxvxxx ekTmNdvdNvf22122)(-⎪⎭⎫⎝⎛==∴π同理可得：kTmvzkTmvyvyzyy ekTmvfekTmNdvdNvf221221222)(2)(--⎪⎭⎫⎝⎛=⎪⎭⎫⎝⎛==ππ例题：用麦克斯韦速度分布律求每秒碰到单位面积器壁上的气体分子数。
