当前位置：文档之家 › 力矩的功,刚体绕定轴转动的动量定理

力矩的功,刚体绕定轴转动的动量定理

  • 格式：ppt
  • 大小：456.50 KB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

刚体定轴转动的角动量定理和角动量守恒定律

刚体定轴转动的角动量定理和角动量守恒定律

刚体定轴转动的角动量定理和角动量守恒定律
1、刚体定轴转动的角动量
刚体绕定轴转动的角动量等于刚体对该轴的转动惯量与角速度的乘积；方向与角速度的方向相同。

2、刚体定轴转动的角动量定理
（1）微分形式：刚体绕某定轴转动时，作用于刚体的合外力矩，等于刚体绕该定轴的角动量随时间的变化率。

（2）积分形式：当物体绕某定轴转动时，作用在物体上的冲量矩等于角动量的增量。

3、刚体定轴转动的角动量守恒定律
如果物体所受的合外力矩等于零，或者不受外力矩作用，物体的角动量保持不变。

练习：1角动量守恒的条件是 。

0=M 11222
1ωωJ J Mdt t t -=⎰刚体 ） 21J J ==ωJ 恒量
ωJ L =()ωJ dt d dt dL M ==。

(完整版)刚体转动守恒定律

(完整版)刚体转动守恒定律

速度0＝0，下摆到竖直位置时的角速度为 ，按 力矩的功和转动动能增量的关系式得
定轴转动的动能定理
mg l 1 J 2
22
由此得 mgl
J
因 J 1 ml 2 代入上式得 3g
3
J
所以细棒在竖直位置时，端点A和中心点C的速度
分别为
vA l 3gl
vC
l
2
1 2
3gl
刚体的平面平行运动
c.若系统内既有平动也有转动现象 发生，若对某一定轴的合外力矩为 零,则系统对该轴的角动量守恒。
定轴转动刚体的角动量守恒定律
直线运动与定轴转动规律对照
质点的直线运动
v dx dt
dv d2 x a dt dt2
P mv F
EK
1 mv2 2
m
dA Fdx Fdt
刚体的定轴转动
d
dt
d
dt
Mz
dLz dt
t2 Mdt t1
L2 L1
dL
L2
L1
角动量定理的微分形式：
t2 t1
M
d
t
J
J0
t2 M d t为t t2 t1时间内力矩M 对给定轴的冲量矩
t1
。
2. 定轴转动刚体的角动量守恒定律
角动量守恒定律：若一个系统一段时间内
所受合外力矩M 恒为零，则此系统的总角 动量L 为一恒量。
解 先对细棒OA所受的力
作一分析；重力G 作用在 O
棒的中心点C，方向竖直向
下；轴和棒之间没有摩擦
力，轴对棒作用的支承力N
垂直于棒和轴的接触面且
通过O点，在棒的下摆过
G
程中，此力的方向和大小

1-4 力矩做功 动能定理 动量守恒定理解析

1-4 力矩做功 动能定理 动量守恒定理解析

刚体定轴转动的动能定理：总外力矩对刚体所做的功等于刚
体转动动能的增量。
例1:如图，冲床上配置一质 量为5000kg的飞轮， r1=0.3m, r2=0.2m.今用转速 为900r/min的电动机借皮带 传动来驱动飞轮，已知电动 机的传动轴直径为d=10cm。 （1）求飞轮的转动动能。
2 r1 2 r
1 1 2 2 ml mvl ml 3 3
2
d
第一章 力学基本定律
1-4 力矩做功 动能定理 动量守恒定理
解:（1）为了求飞轮的转动动能，需先求出它的转动惯量和转速。因飞轮质量 大部分分别布在轮缘上，由图示尺寸并近似用圆筒的转动惯量公式，得
m 2 1 2 J r1 r2 5000 0.3 2 0.2 2 kg m 2 2 2 325kg m 2
第一章 力学基本定律
1-4 力矩做功 动能定理 动量守恒定理
O
解： 这个问题可分为三个阶段进行 分析。第一阶段是棒自由摆落的过 程。这时除重力外，其余内力与外 力都不作功，所以机械能守恒。我 们把棒在竖直位置时质心所在处取 为势能 零点，用表示棒这时的角速度,则
C
l 1 2 11 2 2 mg J ＝ ml 2 2 2 3
（1）
第二阶段是碰撞过程。因碰撞时间极短，自由的冲力极大， 物体虽然受到地面的摩擦力，但可以忽略。
第一章 力学基本定律
1-4 力矩做功 动能定理 动量守恒定理
这样，棒与物体相撞时，它们组成的系统所受的对转轴O的外 力矩为零，所以，这个系统的对 O轴的角动量守恒。我们用 v 表示物体碰撞后的速度，则
则物体在 d t 时间内转过角位移 d
外力矩所做元功为：
dt

刚体定轴转动的转动定律

刚体定轴转动的转动定律

R
M
h
Hale Waihona Puke 解法一 用牛顿第二运动 定律及转动定律求解.分 析受力如图所示. 对物体m用牛顿第二 运动定律得 mg T ma 对匀质圆盘形滑轮用 转动定律有 TR J 物体下降的加速度的 大小就是转动时滑轮边缘 上切向加速度，所以
o R M

T
h
a
G
a R 物体m 落下h 高度时的速率为
2
3.试求质量为m 、半径为R 的匀质圆环 对垂直于平面且过中心轴的转动惯量. 解 作示意图如右,由于质 量连续分布，所以由转动 惯量的定义得
J R 2dm
m
dm
o
R

2R 0
m R dl 2R
2
mR 2
4.试求质量为m 、半径为R 的匀质圆盘 对垂直于平面且过中心轴的转动惯量. dr 解 如图所示, 由于质 量连续分布，设圆盘的 R l o r 厚度为l，则圆盘的质量 密度为 m 2 R l
r近日 r远日
v近日
解 彗星受太阳引力的作用，而引力通过了 太阳，所以对太阳的力矩为零，故彗星在运 行的过程中角动量守恒. 于是有 r近日 v近日 r远日 v远日 因为 r近日 v近日 ，r远日 v远日
r近日v近日 所以 r远日 v远日
代入数据可, 得
J r 2dm
m

R 0
1 1 4 r 2r ldr R l mR 2 2 2
2
5. 如图所示，一质 量为M 、半径为R 的匀 质圆盘形滑轮，可绕一 无摩擦的水平轴转动. 圆盘上绕有质量可不计 绳子，绳子一端固定在 滑轮上，另一端悬挂一 质量为m 的物体，问物 体由静止落下h 高度时, 物体的速率为多少？

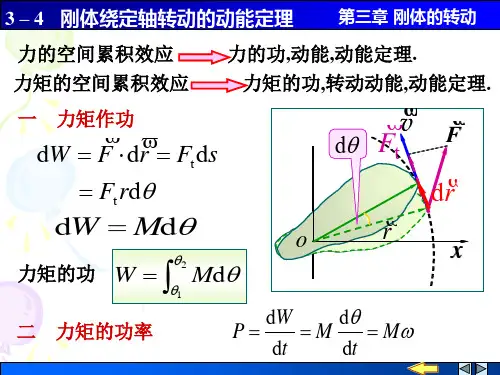
大学物理3_4 刚体绕定轴转动的动能定理

大学物理3_4 刚体绕定轴转动的动能定理
t 3 3 3 5 3 2
3–4
刚体绕定轴转动的动能定理
第三章 刚体的转动
例3 留声机的转盘绕通过盘心垂直盘面的轴以角速度 作匀速转动.放上唱片后,唱片将在摩擦力作用下随转盘一 起转动.设唱片的半径为 R 、质量为 m ,它与转盘间的摩 擦系数为 .求(1)唱片与转盘间的摩擦力矩;(2)唱片达到 角速度 需要多长时间;(3)在这段时间内,转盘的驱动力 矩作了多少功? 解 (1)如图所示,在唱片上取长为 dl 宽为 dr 的面积元 dS dldr ,该面 积元所受的摩擦力为:
1 2 1 2 1 1 1 2 2 2 2 W J J0 mR 0 mR 2 2 2 2 4
3–4
第三章 刚体的转动 刚体绕定轴转动的动能定理 例3-11 一长为 l , 质量为 m0 的均质细竿可绕支点O自 由转动 . 一质量为 m、速率为 v0 的子弹射入竿内一端， 使竿的偏转角为30º 问子弹的初速率为多少 ? .
加速度
力 质量
dr v dt dv a dt
F
d 角速度 dt d 角加速度 dt
力矩

M
m
转动惯量 J
动量
P mv
角动量
L J
r
dm
2
3–4
刚体绕定轴转动的动能定理
第三章 刚体的转动
质点运动规律与刚体定轴转动的规律对照 质点的平动 刚体的定轴转动
EPB EkB EPA EkA
3–4
第三章 刚体的转动 刚体绕定轴转动的动能定理 1 2 4 2 2 J J1 J 2 ml ml ml 3 3
取A点的重力势能为零,即 则有 而
EPA 0

刚体绕定轴转动定律和角动量定理的表达式

刚体绕定轴转动定律和角动量定理的表达式

刚体绕定轴转动定律和角动量定理的表达
式
刚体绕定轴转动定律和角动量定理是物理学中的一对重要定律，它们描述了刚体绕定轴转动的动力学过程。

首先，刚体绕定轴转动定律表明，当刚体绕定轴转动时，角加速度与作用于该刚体的合力成正比，且方向与合力方向一致，可用公式表示为：α=F/I，其中α为角加速度，F为合力，I为惯性矩。

其次，角动量定理表明，刚体绕定轴转动时，角动量的变化量等于作用于刚体的合力矩的积分，可以用公式表示为：ΔL=∫F·ds，其中ΔL为角动量的变化量，F为合力，ds为沿着转动轴的增量。

这两个定律对刚体绕定轴转动的过程有着重要的解释作用。

它们揭示了角加速度与合力之间的关系，以及角动量的变化量与合力矩之间的关系。

同时，它们也为刚体绕定轴转动的动力学研究提供了重要的参考依据，从而为我们更好地理解刚体绕定轴转动的动力学过程提供指导。

总之，刚体绕定轴转动定律和角动量定理是物理学中的重要定律，它们描述了刚体绕定轴转动的动力学过程，并为我们更好地理解刚体绕定轴转动的动力学过程提供指导。

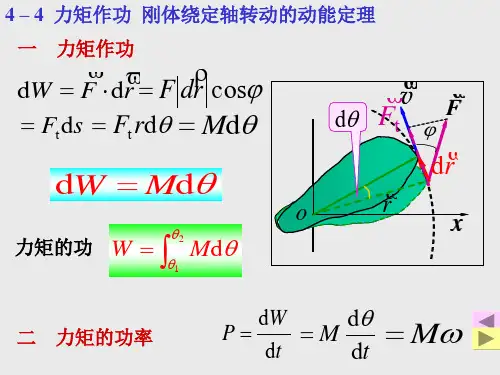
刚体力学_功 动能定理


m
.
N
R
m1
m2 解: 把m1、m2和m看作一系统 系统所受 m g 看作一系统,系统所受 看作一系统 1 m2 g 合外力有重力m 、 合外力有重力 1g、m2g,这两个力对轴 这两个力对轴 支撑力N通过转轴 的力矩分别为m 的力矩分别为 1gR、m2gR;支撑力 通过转轴 对轴的力 、 支撑力 通过转轴,对轴的力 矩为零.加上阻力矩 加上阻力矩M 系统所受合外力矩为 顺时针为正) 系统所受合外力矩为(顺时针为正 矩为零 加上阻力矩 f ,系统所受合外力矩为 顺时针为正 M=m2gR-m1gR-Mf 系统的总角动量为(顺时针为正 顺时针为正) 系统的角 m: Jω 系统的总角动量为 顺时针为正 动量包括 m1: Rm1v L=Jω+Rm1v+Rm2v m2: Rm2v
1 1 1 2 2 2 mv 0 = mv + Jω 2 2 2
的圆盘， 例 一质量为 m' 、半径为 R 的圆盘，可绕一垂 圆盘上绕有轻绳， 直通过盘心的无摩擦的水平轴转动 . 圆盘上绕有轻绳， 问物体由静止下落高度 一端挂质量为m 一端挂质量为 的物体 . 问物体由静止下落高度 h 时， 其速度的大小为多少? 其速度的大小为多少 设绳的质量忽略不计 . v 对圆盘做功， 解1 拉力 FT 对圆盘做功，由刚体绕定轴转动的动 v 能定理可得， 能定理可得，拉力 FT 的力矩所作的功为
o
圆 锥 摆
o
v θ T
'
m
v v
v p
o
v v
R
以子弹和杆为系统 守恒； 动量不守恒； 守恒； 角动量 守恒； 机械能 不守恒 .
圆锥摆系统 守恒； 动量不守恒； 对 O'O 轴角动量 守恒； 守恒； 机械能 守恒 .

44力矩的功刚体绕定轴转动的动能定理


19
7
物理学 教程
4-4 力矩的功 刚体绕定轴转动的动能定理
o
圆 锥 摆
'
圆锥摆系统
动量不守恒；
R
T
m
p
o
v
角动量守恒； 机械能守恒．
8
物理学 教程
4-4 力矩的功 刚体绕定轴转动的动能定理
例：如图，一细绳穿过光滑水平桌面上的小孔O，绳的一端系 有一质量为m的小球并放在桌面上；另一端用力往下拉住。 设开始时小球以角速度0 绕孔O 作半径r 的匀速圆周运动, 现在向下缓慢拉绳，直到小球作圆周运动的半径为r/2时止 求：这一过程中拉力的功。
Mgh
2 Mgh kh h 1 零势面 M m 2 (2)弹簧伸长最大时，M 的速度应为零。上式中令v=0，得弹
1 J mr 2 , v r 2
2
Mv
J kh 2 2
由此解得： v
2
M
簧的最大伸长量为：hmax 2 Mg / k
12
物理学 教程
4-4 力矩的功 刚体绕定轴转动的动能定理
3
细杆绕质心转动的转动惯量： J c 1 Ml 2
(4)
m
联立求解上述方程组

2m v 4m M 0 欲使细杆运动半圈后与小球再次相碰，须使 v1 v2 v2
6mv 0 l ( 4m M )
v1 4m M v0 4m M
(即两者运动一样快)，条件为：M=2m
17
物理学 教程
——刚体绕定轴转动的动能定理
比较
1 1 2 2 W F dr mv2 mv1 2 2
4
物理学 教程
4-4 力矩的功 刚体绕定轴转动的动能定理

刚体的转动


解 以m1 ， m2 ， m 为研究对象
m1g T1 m1a
T2 m2 g m2a
T1r
T2r
J
1 mr2
2
a r
T2
T2
m2
m2 g
(m1 m2 )g
(m1
m2
1 2
m)r
0
t
(m1 m2 )gt
(m1
m2
1 2
m)r
mr
T1
T1
m1
m1 g
17
例4-3:一长为l 质量为m 匀质细杆竖直放置,其下端与一固
0
3
平行轴定理 J z' J z Md2
J z' 刚体绕任意轴的转动惯量
J z 刚体绕通过质心的轴
d 两轴间垂直距离
z
x M,L
O dx
x
L
J
2 L
x2dx
1 12
ML2
2
z' z
M
d C
13
例如圆环绕中心轴旋转的转动惯量
J L R2dm m R2 0
例如圆盘绕中心轴旋转的转动惯量
dl m
R
O
ds 2 rdr
dm ds
dJ r2dm
J
R
dJ
1
mR2
0
2
m
R2
Rm dr
r O
14
例4-1:一轻绳绕在半径r =20 cm的飞轮边缘,在绳端施以F=98 N的拉力, 飞轮的转动惯量 J=0.5 kg·m2,飞轮与转轴间的摩擦不计,求(1)飞轮的 角加速度 (2)如以重量P =98 N的物体挂在绳端,计算飞轮的角加速度
需将力分别向垂直于轴以及平行于轴方向 做正交分解，如图所示

力矩与功

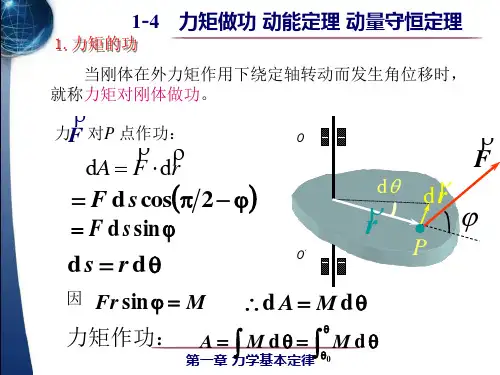
即恒力矩对绕定轴转动的刚体所作的功，等于力矩的大小与转过的角度θ的乘
中，对棒和地球系统，外力（轴对棒）不作功，
由于碰撞时间极短，
轴的角动
经典力学）的确定性。

即如果知道物体初始的运动状态以及运动过程中的受力情况，那么就可以根据牛顿运动定律列出物体的运动方程，从而可以确知物体在任意时刻的运动状态。

事实上，确定性的确取得了大量令人振奋的成就，如哈雷彗星回归时间的预测、海王星的发现、宇宙飞船与空间站的对接和返回地
然而事实上，物体的运动并非都是只按照确定性进行的，在许多情况下，物体的运动还表现出相当明显的偶然性、随机性。

例如，作抛体运动的物体的运动轨迹会因为空气的阻力、温度和湿度、风速等因素的影响而发生随机的变化。

表现物体运动随机性的最典型的例子是布朗运动。

如图是藤黄粒子在水中
x3
图（1）
222ωJ
3l Mg
2。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

3-3 力矩的功 刚体绕定轴转动的动能定理
解3 ： W Md
0


l mg sin d 0 2 l mg （ 1 cos ） 2

m,l θ O mg
W
2
1
1 2 1 2 Md I 2 I 1 2 2
1 2 l 3g I mg （ 1 cos ） ω (1 cos θ )13 2 2 l
2
3 刚体绕定轴转动的功能原理
刚体动能与势能之和为刚体的机械能，
E Ek E p
考虑到刚体内力不做功，由质点系功能原理得
W外 E E0 称刚体的功能原理
5
3-3 力矩的功 刚体绕定轴转动的动能定理
W外 E E0 称刚体的功能原理
若外力矩不作功，则刚体的机械能守恒 讨论
子细 弹绳 击质 入量 沙不 袋计
3-3 力矩的功 刚体绕定轴转动的动能定理
力的时间累积效应： 冲量、动量、动量定理． 力矩的时间累积效应： 角冲量、角动量、角动量定理． 力的空间累积效应： 力的功、动能、动能定理． 力矩的空间累积效应： 力矩的功、转动动能、动能定理．
1
3-3 力矩的功 刚体绕定轴转动的动能定理
3-3 力矩的功 刚体定轴转动的动能定理
W Md
1
2
1
1
2 d I d I d 1 dt
W
2
1
1 2 1 2 Md I 2 I 1 2 2
4
——刚体绕定轴转动的动能定理
3-3 力矩的功 刚体绕定轴转动的动能定理
比较
1 2 1 2 W Md I 2 I 1 1 2 2 1 1 2 2 W F dr mv2 mv1 2 2
一
dW F dr F ds F rd
dW Md
1、力矩的功
力矩的功
v
d
F
F
dr
o
2
r
x
W Md
1
2
3-3 力矩的功 刚体绕定轴转动的动能定理
dW d P M M 2 力矩的功率 dt dt 比较 W F dr P F v
o
以子弹和沙袋为系统 动量守恒；
v
角动量守恒； 机械能不守恒 .
6
3-3 力矩的功 刚体绕定轴转动的动能定理
以子弹和杆为系统
子 弹 击 入 杆
o
动量不守恒；
角动量守恒；
v
机械能不守恒．
7
3-3 力矩的功Βιβλιοθήκη 刚体绕定轴转动的动能定理o
圆 锥 摆
'
圆锥摆系统
动量不守恒；
R
T
m
p
o
v
3-3 力矩的功 刚体绕定轴转动的动能定理
解2 ： M d L
l dL mg sin 2 d l dL mg sin d 2 L I l I d mg sin d 2
dt
m,l O
FN
θ
mg
3g ωdω sin θdθ 2l 3g 代入初始条件积分得 ω (1 cos θ ) 12 l
3 转动动能
1 2 Ek mi vi i 2 1 1 2 2 2 ( mi ri ) I 2 i 2
3
3-3 力矩的功 刚体绕定轴转动的动能定理
二 刚体的功能原理 1、刚体的势能 在重力场中，物体的势能等于质心的势能； 保守力对刚体作功等于刚体势能增加的负值。
2、刚体绕定轴转动的动能及动能定理
1 3mva 2 2 mva ( ml ma ) 2 2 3 m'l 3ma
15
3-3 力矩的功 刚体绕定轴转动的动能定理
射入竿后，以子弹、细 杆和地球为系统，E =常量．
o
30

1 1 2 2 2 ( ml ma ) 2 3
o
a
m v
'
l o mga (1 cos30 ) mg (1 cos 30 ) 2
v g (2 3 )( ml 2ma )( ml 3ma ) 6 ma
2 2
16
3-3 力矩的功 刚体绕定轴转动的动能定理
三、刚体功能原理的应用 P114 例3.3.1；3.3.2
14
3-3 力矩的功 刚体绕定轴转动的动能定理
例1 一长为 l , 质量为m o 的竿可绕支点O自由转动．一 30 质量为m’、速率为v 的子弹射 a ' 入竿内距支点为a 处，使竿的 m o 偏转角为30 . 问子弹的初速 v 率为多少? 解 子弹、竿组成一系统，应用角动量守恒
10
3-3 力矩的功 刚体绕定轴转动的动能定理
解1：M I
l mg sin I 2
1 I ml 3
2
m,l
FN
θ
3g sin 得 2l
dω 3 g ω sin θ dθ 2l
O
mg
3g ωdω sin θdθ 2l 3g 代入初始条件积分得 ω (1 cos θ ) 11 l
角动量守恒； 机械能守恒．
8
3-3 力矩的功 刚体绕定轴转动的动能定理
课堂练习 用刚体绕定轴转动的动能定理重解3-2 例5第二问.
9
3-3 力矩的功 刚体绕定轴转动的动能定理
3-2例5 一长为 l 、质量 为 m 匀质细杆竖直放置， m,l 其下端与一固定铰链O相 θ 接，并可绕其转动．由于 mg O 此竖直放置的细杆处于非 稳定平衡状态，当其受到微小扰动时，细 杆将在重力作用下由静止开始绕铰链O 转 动．试计算细杆转动到与竖直线成 角时 的角速度．