当前位置：文档之家 › 刚体绕定轴转动力矩课件

刚体绕定轴转动力矩课件

  • 格式：ppt
  • 大小：1.23 MB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

§5.2-力矩---刚体绕定轴转动微分方程

§5.2-力矩---刚体绕定轴转动微分方程
F f m a i i
的切向加速度，质元沿
法向运动的科里奥里加
i
i
速度（定轴转动刚体没 有这种运动）
圆周轨迹切线投影
Fi fi miai
同乘以 ri
Fi ri fi ri miai ri miri2β ai=ri
对所有质元求和
Fi ri fi ri ( miri2 )β
根据牛顿第二定律，第 i 个质元
外内
力 Fi
力 fi
miai
圆周轨迹切线投影
同乘以 ri
Fi fi miai Fi ri fi ri miai ri miri2β
ai=ri
对所有质元求和
Fi ri fi ri ( miri2 )β
§6.1 力矩
一. 力矩
力
?
加速度 角加速度
质点运 动状态 的改变
转动刚体 状态的改
变
刚体绕定轴转动微分方程
z
F//
F
hr

M z (F ) F r
F F Fn
Fh
力矩是代数量 使刚体逆时针加速转动，为正数；否则为负。 力矩取决于力的大小、方向和作用点位置
二. 刚体定轴转动微分方程
它在水平位置
求 它由此下摆 角时的 解 dm 质元 dm m dx
l
dm 重力矩 dM gdm x cos
O
ml

x
M
dM

1 2
mgl cos
gdm
重力对整个棒的合力矩等于重力全部 集中于质心所产生的力矩
转动定律 M
J J 1 ml2
3

力矩 刚体绕定轴转动定律-精品文档

力矩 刚体绕定轴转动定律-精品文档
力矩 刚体绕定轴转动定律
一、刚体绕定轴转动的力矩
z
F//
F
F对点O转动的力矩:
MO
O
Mz
y
x
r
P
F
F对定轴z转动的力矩:
M r F O r F r F //
M r F z
二、定轴转动定律
M β z J
M J Fr 2 M Fr 39 . 2 [ rad /s ]
mg T ma
Tr J
J
r
O
T
F
mg
(2)
ar
21 . 8 [ rad /s]
2
例: 均匀细直棒m 、l ，可绕轴 O 在竖直平面内转动 初始时它在水平位置 m l O 求: 它由此下摆 角时的
转动惯量与转轴有关
例: 求圆环绕中心轴旋转的转动惯量
2 解: dm 转动惯量 d JR d m
2 J R d m R d m mR 2 2 0 0 L L
dl R o
m
例: 求圆盘绕中心轴旋转的转动惯量 m 2 mr m d S 解: d 2 2πrdr 2 dr πR R dm 转动惯量 d J r2d m
M r d f df 的力矩 d
R
2 d M mgR 圆盘摩擦力矩 M 0 2 1 2d 3 mgR mR
d M

d 3 转动定律 MJ dt 3R0 t 0 3 R t d t d 0 4g g 04
2
d t
例: 一均质棒，长度为 l，现有一水平打 击力F 作用于距轴 l 处。 求: l =? 时, 轴对棒作用力的水平分量为 0。

物理课件2.91刚体的定轴转动力矩转动定律转动惯量

物理课件2.91刚体的定轴转动力矩转动定律转动惯量
物理ppt课件2.91 刚体的定轴转动力 矩转动定律转动惯 量
目录
• 刚体的定轴转动 • 力矩 • 转动定律 • 转动惯量
01
刚体的定轴转动
刚体的定义
刚体
在任何力的作用下，其形状和大 小都不会发生变化的物体。刚体 是一个理想化的物理模型，用于 简化对物理现象的研究。
刚体的特点
刚体在力的作用下，只发生平动 或定轴转动，不会发生形变。在 刚体的定轴转动中，其上任意两 点之间的距离保持不变。
刚体的定轴转动
定轴转动
刚体绕某一固定轴作转动。
定轴转动的特点
刚体在定轴转动中，其上任意一点都绕同一固定轴作圆周运动，且各点的角速 度相同。
刚体的定轴转动定律
刚体的定轴转动定律
转动惯量
刚体绕固定轴转动的角动量守恒。即 刚体在不受外力矩作用时，其角动量 保持不变。
描述刚体转动惯性的物理量，等于刚 体质量与质心到转轴距离平方的乘积 。
转动惯量
描述刚体绕定轴转动的惯性大小的物理量。
转动惯量的定义公式
I = Σ (m * r^2)，其中I是转动惯量，m是质量， r是质点到转轴。
转动惯量的计算
对于细杆，若其质量分布均匀，则其 转动惯量等于质量与质心到转轴距离 平方的乘积。
对于质量分布不均匀的刚体，需要将 刚体分割成若干微元，然后对每个微 元应用转动惯量的定义公式进行计算 。
对于质量分布均匀的圆盘，其转动惯 量等于圆盘质量与半径平方的乘积。
转动惯量的应用
在动力学问题中，转动惯量是描 述刚体转动状态的重要物理量， 可以用于计算刚体的角速度、角
加速度等物理量。
在振动问题中，转动惯量可以影 响刚体的振动频率和振幅。
在陀螺仪和电机控制等领域，转 动惯量也是重要的参数之一。

刚体定轴转动的转动定律力矩

刚体定轴转动的转动定律力矩

力矩平衡的条件
静平衡
刚体在转动过程中，如果合力矩 为零，则刚体保持静止状态。
动平衡
刚体在转动过程中，如果合力矩为 零，则刚体保持匀速转动状态。
平衡状态
无论是静平衡还是动平衡，刚体的 平衡状态都满足合力矩为零的条件。
力矩平衡的应用
机械平衡
在机械设计中，通过调整刚体的质量 分布或添加平衡装置，使刚体在转动 过程中满足力矩平衡条件，以保证机 械设备的稳定性和可靠性。
刚体的定轴转动
定轴转动：刚体绕某一固定轴线作旋 转运动。
在定轴转动中，刚体的角速度和角加 速度是矢量，其方向沿固定轴线，而 力矩是改变刚体转动状态的唯一物理 量。
刚体定轴转动的特点
角速度矢量、角加速度矢量和力 矩矢量都与固定轴线平行。
刚体定轴转动时，其上各点的速 度方向与该点到轴线的垂直线段 相垂直，各点的加速度方向与该
实例三：旋转木马的旋转
总结词
旋转木马的旋转是刚体定轴转动的又一实例，通过外力矩的作用，使旋转木马绕轴转动。
详细描述
旋转木马在外力矩的作用下开始转动，当旋转木马转动时，由于摩擦阻力和空气阻力的作用，旋转木 马会逐渐减速并最终停止。
实例四：陀螺的稳定旋转
总结词
陀螺的稳定旋转是刚体定轴转动的最后一个实例，陀螺通过自转保持稳定的旋转状态。
在日常生活和工业生产中，转动 定律也广泛应用于各种旋转运动
的分析和设计。
04
刚体定轴转动的力矩平衡
力矩平衡的概念
力矩平衡
刚体在转动过程中，受到 的力矩之和为零，即合力 矩为零。
力矩
力对转动轴的力矩等于力 和力臂的乘积，其中力臂 是从转动轴到力的垂直距 离。
转动轴
刚体转动的中心轴，可以 是固定的点或线。

《刚体绕定轴转动》课件

《刚体绕定轴转动》课件
对于多个物体组成的系统，其转动惯量等于 各个物体转动惯量的矢量和。
转动惯量是惯性大小的量度
转动惯量越大，刚体越不容易改变其转动状 态。
转动惯量的平行轴定理
刚体绕某轴转动时，其转动惯量与通过质心 并与该轴平行的轴的转动惯量相同。
转动惯量的应用
在动力学中的应用
通过计算刚体的转动惯量，可 以求得刚体在力矩作用下的角
转动惯量的定义：描述刚体绕定轴转动惯性大小的物理 量。
转动惯量的单位：kg*m^2。
转动惯量的计算公式：I=∑mr^2，其中m为质量，r为 质点到转轴的距离。
转动惯量的特点：只与刚体的质量和各质点到转轴的距 离有关，与转动角速度和转动的加速度无关。
转动惯量的性质
转动惯量是标量
没有方向，只有大小。
转动惯量具有叠加性
势能的特点
与物体的质量、转动惯量和角速度 有关。
动能与势能的关系
动能与势能可以相互转化，满足能量 守恒定律。
动能与势能的转化关系可以通过动力 学方程式表示，如牛顿第二定律等。
在刚体绕定轴转动过程中，动能和势 能之间可以相互转化，但总能量保持 不变。
CHAPTER
04
刚体绕定轴转动的转动惯量
转动惯量的定义与计算
3
角动量守恒的条件
系统不受外力矩作用或外力矩的矢量和为零。
角动量守恒定律的应用
天体运动
行星绕太阳的公转、卫星绕地球的轨道运动等都 遵循角动量守恒定律。
陀螺仪
利用角动量守恒定律，陀螺仪可以保持自身的旋 转轴指向一个固定的方向。
机械系统
在机械系统中，通过合理设计，可以利用角动量 守恒定律来优化系统的运动性能。
飞机的飞行控制
飞行员通过操作杆施加力矩，改 变机翼的攻角，实现飞机的升降

刚体定轴转动的转动定律力矩PPT

刚体定轴转动的转动定律力矩PPT

求 θ角及着陆滑行时的速度多大？
解 引力场（有心力）
v0
系统的机械能守恒
质点的动量矩守恒
m r0
v R
OM
m 1 2m v v 0 r 00 2s iGπ n r0 M) ( 1 2 m m m vv 2 R GRMm vv0r0R sin4v0sin
sin14123RGv0M 21/2
1/2
LZ Δmiviri Δmiri2 JZ
i
i
LZJZ(所有质元对 Z 轴的动量矩之和)
2. 刚体定轴转动的动量矩定理
对定轴转动刚体，Jz 为常量。
dLZ dt
JZ
d
dt
dLZ dt
Mz
M zd t d L z d J
动量矩定理 微分形式
t1 t2M zd t 1 2d JJ2 J1（动量矩定理积分形式）
0tm1m 1m 2m 21 2 gmtr
3.2.2 刚体定轴转动的动能定理
1. 刚体定轴转动的动能
Δ m 1 ,Δ m 2 ,,Δ m k ,,Δ m N r 1 ,r 2 ,,r k ,,r N v 1 , v 2 , , v k , , v N
Δmk 的动能为
Ek 12Δmkvk212Δmkrk22
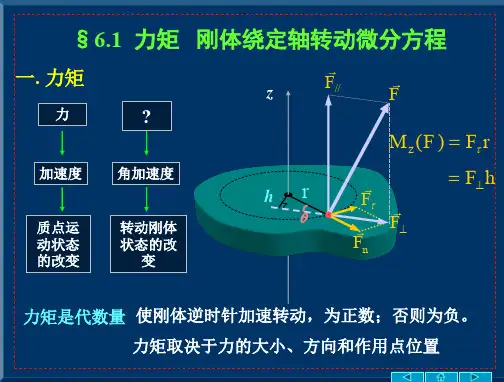
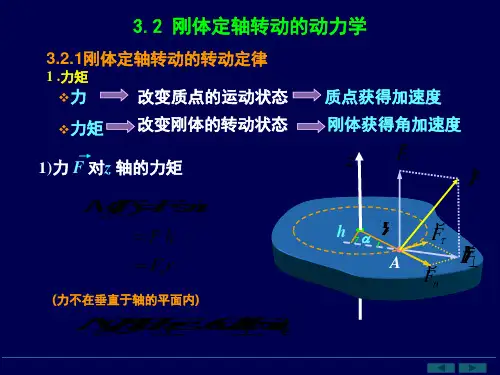
F FF Fn
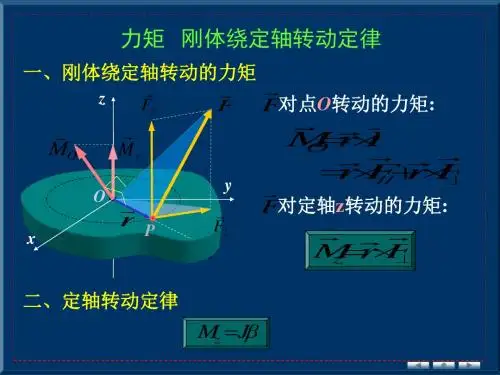
2)力对点的力矩
Mo
M O r F
F
大小 M OrF sin
O . r
指向由右螺旋法则确定 力对定轴力矩的矢量形式
z
F//
F
M Z r F
（力对轴的力矩只有两个指向）
r
A
FF
2. 刚体定轴转动的转动定律
第 k个质元 F k f k m k a k

刚体的定轴转动-力矩

刚体的定轴转动-力矩

力Hale Waihona Puke 的计算公式总结词力矩的计算公式为 M = r × F，其中 r 是 从转动轴到力的矢量，F 是施加在刚体上 的力。
VS
详细描述
力矩的计算公式是 M = r × F，其中 r 是 从转动轴到力的矢量，F 是施加在刚体上 的力。这个公式表明，力矩的大小不仅取 决于力的绝对值和力臂的大小，还取决于 力和力臂之间的夹角。
角动量定理
力矩是改变刚体角动量的原因，力矩与角动量的变化率成正比。
角动量守恒定律
在没有外力矩作用的情况下，刚体的角动量保持不变。
力矩与角速度的关系
力矩与角加速度的关系
力矩等于刚体转动惯量与角加速度的乘积。
角速度定理
力矩作用在刚体上，将引起刚体的角速度变化，力矩与角速度的变化率成正比。
力矩与转动惯量的关系
转动惯量的定义
转动惯量的计算公式
转动惯量是描述刚体转动惯性大小的物理量， 与刚体的质量分布和转动轴的位置有关。
对于一个质量为m、距离转动轴距离为r的 质点，其转动惯量为mr^2。
05
力矩的平衡
刚体定轴转动的平衡条件
平衡条件
对于刚体上的任意一点，力矩矢量和为零。
平衡状态
刚体在定轴转动时，其角速度矢量和为零。
刚体的定轴转动-力矩
• 引言 • 力矩的基本性质 • 力矩的分类 • 力矩与刚体转动的关系 • 力矩的平衡 • 刚体的定轴转动实例
01
引言
定义与概念
01
02
03
定义
力矩是一个描述力的转动 效果的物理量，表示力和 力臂的乘积。
符号
通常用M表示力矩，L表 示力臂。
单位
国际单位制中的单位是牛 顿米（N·m）。

《刚体的定轴转动》课件

《刚体的定轴转动》课件

实例二
陀螺在受到外力矩作用后发生定轴转动。分析过程中应用了转动定 律，解释了陀螺的进动现象。
实例三
电风扇在启动时，叶片的角速度从零逐渐增大到稳定值。分析过程中 应用了转动定律，解释了电风扇叶片角速度的变化规律。
CHAPTER
03
刚体的定轴转动的动能与势能
动能与势能的定义
动能定义
物体由于运动而具有的能量，用 符号E表示，单位是焦耳(J)。
势能定义
物体由于相对位置或压缩状态而 具有的能量，常用符号PE表示， 单位是焦耳(J)。
刚体的定轴转动动能与势能的计算
转动动能计算
刚体的转动动能等于刚体绕定轴转动的动能，等于刚体质量与角速度平方乘积的一半， 即E=1/2Iω^2。
势能计算
刚体的势能等于刚体各质点的势能之和，等于各质点的位置坐标与相应的势能函数的乘 积之和。
01
数学表达式：Iα=M
02
转动惯量的计算：根据刚体的质量和形状，可以计算出其转动
惯量。
角加速度的计算：根据作用在刚体上的外力矩和刚体的转动惯
03
量，可以计算出其角加速度。
转动定律的实例分析
实例一
匀速转动的飞轮在受到阻力矩作用后，角速度逐渐减小，直至停止 转动。分析过程中应用了转动定律，解释了飞轮减速直至停止的原 因。
CHAPTER
02
刚体的定轴转动定律
转动定律的内容
刚体定轴转动定律
对于刚体绕固定轴的转动，其转动惯量与角加速度乘积等于作用 在刚体上的外力矩之和。
转动定律的物理意义
描述了刚体在力矩作用下绕固定轴转动的运动规律。
转动定律的适用范围
适用于刚体在力矩作用下的定轴转动，不适用于质点和弹性体的转 动。

力矩转动定律 PPT

力矩转动定律 PPT

解：
物体由斜面顶端滚下, 可视为质心的平动和 相对质心的滚动两种 运动合成.
y

N
x
Ff
C
mg
aC

22
质心运动方程
mg sin Ff maC
转角动量定、律线量F关f 系R J a aC R
y

N
x
Ff
C
mg
aC

ma

mg
sin


Ja R2
a

mgR2 mR2
结束21
*P98例4 如图一斜面长 l = 1.5m, 与水平面的夹角θ= 5o.
有两个物体分别静止地位于斜面的顶端, 然后由顶端沿
斜面向下滚动, 一个物体是质量 m1 = 0.65kg、半径为R1 的实心圆柱体, 另一物体是质量为 m2 = 0.13 kg 、半径 R2 = R1 = R 的薄壁圆柱筒. 它们分别由斜面顶端滚到斜 面底部各经历多长时间?
圆柱比圆筒先到达底部24.
补充例题 一个飞轮的质量 m＝60kg，半径为R＝0.25m，
正在以ω0＝1000r/min的转速转动，现在要制动飞轮，要
求在 t ＝5.0s内使它均匀减速而最后停下来。求闸瓦对轮
子的压力N为多大？假使闸瓦与飞轮之间的滑动摩擦系数
为μk＝0.8，而飞轮的质量可以看作全部均匀分布在轮的
P96 表4-1列出了一些均匀刚体的转动惯量 .
平行轴定理
质量为m的刚体，如果对 其质心轴的转动惯量为 Jc，则 对任一与该轴平行，相距为d 的转轴的转动惯量
d
C mO
JO JC md 2 （证明略）
例：圆盘对P 轴的转动惯量

刚体的定轴转动力矩课件

刚体的定轴转动力矩课件

大小
力矩的大小与力的大小、力臂长 度以及力和转动轴之间的夹角有
关。
转动效应
力矩能够使刚体绕固定轴转动， 改变刚体的角速度和角动量。
定轴转动力矩的应用
机械传动
在机械传动中，如齿轮、蜗轮等，定轴转动力矩 是实现能量传递和运动转换的关键因素。
航空航天
在航空航天领域，定轴转动力矩用于控制飞机的 飞行姿态和稳定飞行状态。
平衡条件
为了保持刚体的定轴转动，必须满足力矩平衡条件，即重力矩与阻力矩相等。
实例分析
以钟摆为例，钟摆在重力作用下绕轴转动，为了保持钟摆的定轴转动，钟摆的长度和重 力的作用点必须满足一定的条件，否则钟摆会发生摆动。
THANKS
感谢观看
力矩平衡条件
对于旋转机械，力矩平衡是保持机械稳定运转的重要条件，即作用 在刚体上的所有力矩之和为零。
实例分析
以电动机为例，电动机在运转过程中，作用在电动机转子上的电磁力 矩与转子受到的阻力矩平衡，使得电动机能够稳定运转。
刚体在重力作用下的定轴转动
重力对刚体的作用
重力是作用在刚体上的恒力，当刚体在重力作用下绕轴转动时，重力会产生一个力矩。
刚体的动态平衡
总结词
刚体在运动状态下，受到的力矩和力矩的冲量之和为零。
详细描述
刚体的动态平衡是指刚体在运动状态下，受到的力矩和力矩的冲量之和为零。这意味着作用在刚体上 的所有力矩和力矩的冲量在某一时间段内相互抵消，使刚体保持匀速直线运动或匀速转动状态。
刚体的稳定性和失稳条件
总结词
刚体在受到微小扰动后能恢复到原来的平衡状态的性质。
刚体的分类
可分为固定刚体和活动刚 体。
刚体的定轴转动
定轴转动定义
刚体绕某一固定轴线作转动。

力矩 刚体绕定轴转动微分方程

力矩 刚体绕定轴转动微分方程

r r
v F
P
h
θ
• •
力矩是矢量 —— 反映力的大小、方向和作用点 反映力的大小、 在刚体的定轴转动中， 在刚体的定轴转动中，力矩矢量只有两个指向
讨论 (1) 力对点的力矩 —更为一般的物体转动
r Mo
O .
r F
r r r MO = r ×F
(2) 力对定轴的力矩
r r r 力对轴的力矩 力矩为 力对轴的力矩为 MZ = r' ×F ⊥
M −Tr = J1β 1 2 J1 = mr 1 2
µ
α N f T T m2g m1g N M
对物体 使用牛顿定律
T − µm gcosα −m gsinα = m a 2 2 2
a = rβ 2 M −m gr(sinα + µcosα)] [ 2 β= (m +2m )r2 1 2
[2M + m gr(sinα + µcosα)]m 1 2 T= (m + 2m )r 1 2 2 M −m gr(sinα + µcosα)] dω dω dϕ [ 2 = ⋅ = β= 2 dt dϕ dt (m +2m )r 1 2 dω 4 [M −m gr(sinα + µcosα)] φ 2 ⋅ω ω= dϕ (m + 2m )r2
m 解 dm= dx df = µdm⋅ g m L L m 根据力矩 dM′ = −µ ⋅ gxdx O x L L m 1 dx ′ = ∫ −µ ⋅ gxdx = − µm M gL 0 L 2
ω
x
•
在定轴转动中， 在定轴转动中，力矩可用代数值进行计算
T T'
例如 T' T T' T

力矩_刚体定轴转动定律

力矩_刚体定轴转动定律

m2
m1
1 2
m
r
当不计滑轮质量及摩擦阻力矩即令m=0、M=0时，
有
T1
T2
2m1m2 m2 m1
g
a m2 m1 g m2 m1
上题中的装置叫阿特伍德机，是一种可用来测量
重力加速度g的简单装置。因为在已知m1、 m2 、r和 J的情况下，能通过实验测出物体1和2的加速度a，
再通过加速度把g算出来。在实验中可使两物体的m1 和m2相近，从而使它们的加速度a和速度v都较小， 这样就能角精确地测出a来。
注 （1）在定轴动问题中 ，如不加说明，所指的力矩 是指力在转动平面内的分力 对转轴的力矩。
力矩
（2） M Z rF2 sin F2d
d r s是in转轴到力作用线
F1 F
的距离，称为力臂。
（3） F1 对转轴的力矩为零，
在定轴转动中不予考虑。
转动 平面
rF2ຫໍສະໝຸດ （4）在转轴方向确定后，力对 转轴的力矩方向可用+、-号表示。
的质量dm=rddre，所受到的阻力矩是rdmg 。
定轴转动定律
此处e是盘的厚度。圆盘所受阻力矩就是
M rdmg g rreddr
ge02
d
R
0
r
2dr
2 geR3
3
因m=eR2，代入得
M
2 mgR
3
根据定轴转动定律，阻力矩使圆盘减速，即
获得负的角加速度.
定轴转动定律
2 mgR J 1 mR2 d
N
firi sin i 0
i1
定轴转动定律
得到：
N
Firi
sin i
N
(mi
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

若 F 使刚体逆时针转 若 F 使刚体顺时针转
M z 为正 M z为负
例如
T

T'
M i TR T' R
讨论
T
T'
i
M
Tr T ' R
F
1)力平行于转轴或通过转轴时，对该轴力矩为零。 z F// F//不能改变刚体绕z轴的转动状态 F// 对z轴的力矩为零
例 刚体绕 z 轴正向转动， n 60r / min ，某时刻 p点位矢
r 3i 4 j 5k (m)
求 p点的速度 解
2n 2 rad / s 60 k 2k （∵ 沿 z 轴正向转）
v r 2k (3i 4 j 5k ) 8i 6j (m / s)
II
M
当
βc
0 t 1 2 ( ) t t 0 2 2 2 0 2 ( 0 )
z ω,
与质点的匀加速直线运动公式相像
二. 定轴转动刚体上各点的速度和加速度
任意点都绕同一轴作圆周运动, 且 ， 都相同 O
z
ω,
v
P
• 加速度与角加速度的矢量关系式
dv d(ω r ) a dt dt dω dr r ω dt dt
O
刚体
r'
r
×O
定轴
β r ω v
aτ r
an v
d dt

③ 直角坐标系中，设刚体绕 z 轴作定轴转动，则角速度矢量为
k 的方向 0 沿 z正向 0 沿 z负向
d k dt
角加速度矢量为
④ 定义了角速度矢量后，就可以用它表示出刚体上任意点的 速度
d r v ω r dt
§5.3 刚体绕定轴转动
刚体内各点都绕同一直线(转轴)作圆周运动___刚体转动
转轴固定不动 — 定轴转动
刚体的平动和绕定轴转动是刚体的 两种最简单最基本运动
z
一. 描述 刚体绕定轴转动的角量
角坐标 角速度 角加速度
f (t )

d f ' (t ) dt
I

P
d d 2 2 f " (t ) d t dt
吊箱平动
x A xB R cos(t 0 ) y A yB L R sin(t 0 ) L
2 xA ( y A L) 2 R 2
v Ax v Ay
dx A R sin(t 0 ) dt dy A R cos(t 0 ) dt
i=3 y x O
z
y i = 3+2+1= 6
当刚体受到某些限制 ——自由度减少
§5.2 刚体的平动
刚体运动时，若在刚体内所作的任一条直线都始终保持和自 身平行 — 刚体平动 平动的特点 (1) 刚体中各质点的 运动情况相同
rA rB z rA rB BA v A vB O a A aB x
力对定点o的力矩
Mo
O .
F
r
说明：可以证明：力对任意点的力矩，在通过该点的任一
2)若 F 不在垂直于z轴的平面内
F F F//
o r h A
F
M z ( F ) M z ( F ) F h
③ 也可将力 F (位于垂直于z轴的面内)对z轴的力矩视为
矢量，定义矢量力矩 大小：rF sin
MZ r F
2 Ax
vA v
v
2 Ay
25 R 0.26 m / s 300
dv Ax a Ax R 2 cos(t 0 ) dt dv Ay a Ay R 2 sin(t 0 ) dt 2 25 2 2 2 3 2 a A a Ax a Ay R 2.7 10 m / s 2 300
第5章 刚体运动学
§5.1 刚体和自由度的概念
一. 刚体 —— 力的作用下形状和大小不变的物体
特殊的质点系， 形状和体积不变化。在力作用下，组成 物体的所有质点间的距离始终保持不变 —— 理想化模型
二. 自由度
确定物体的位置所需要的独立坐标数 —— 物体的自由度数 z s O x i=1 i=2
(x,y,z) O
刚体
v
P
r'
v r' an r ' 2 dv a r' dt
r
×O

角速度与角加速度的矢量表示
① 对于角速度矢量，规定：角速度矢量的大小就是角速度的 大小，方向沿转轴方向，其指向由右手螺旋法则确定：右 手四指指向刚体转动方向，拇指指向为 方向。 ② 角加速度矢量
第6章 刚体动力学
§6.1 力矩 刚体绕定轴转动微分方程
一. 力矩
• •
力
改变质点的运动状态 改变刚体的转动状态
质点获得加速度 刚体获得角加速度
力 F 对z 轴的力矩
z
o h r A
F
M z ( F ) Fh Fr sin
±”的确定：（右螺旋） •“ 从z轴正端向负作用点的位矢 ： r 和 F 的夹角
当 F 不在垂直于z轴的平面内
M Z r F
MO r F 大小： M o M o rF sin 方向：垂直于 r 和 F 所确定
的平面，且指向由右 螺旋法则给出。
A
A
rA B rB
A
y
B
B
(2) 刚体的平动可归结为质点运动
例 一大型回转类“观览圆盘”如图所示。圆盘的半径R=25 m， 供人乘坐的吊箱高度 L=2 m。若大圆盘绕水平轴均速转动， 转速为0.1 r/min。 求 吊箱底部A点的轨迹及A点的速度和加速度的大小。 解
2π 2π π T 10 60 300