等比数列复习教案

等比数列及其前n 项和1．等比数列的有关概念 (1)定义：如果一个数列从第2项起，每一项与它的前一项的比等于同一常数(不为零)，那么这个数列就叫做等比数列．这个常数叫做等比数列的公比，通常用字母q 表示，定义的表达式为a n ＋1a n ＝q .(2)等比中项：如果a 、G 、b 成等比数列，那么G 叫做a 与b 的等比中项．即：G 是a 与b 的等比中项⇔a ，G ，b 成等比数列⇒G 2＝ab . 2．等比数列的有关公式 (1)通项公式：a n ＝a 1q n －1.(2)前n 项和公式：S n ＝⎩⎪⎨⎪⎧na 1，q ＝1，a 1(1－q n )1－q＝a 1－a n q 1－q ，q ≠1.1．在等比数列中易忽视每项与公比都不为0.2．在运用等比数列的前n 项和公式时，必须对q ＝1与q ≠1分类讨论，防止因忽略q ＝1这一特殊情形导致解题失误． [试一试]1．在1和9之间插入三个正数，使这五个数成等比数列，则插入的三个数的和为________．2．(2014·徐州摸底)已知各项均为正数的等比数列{a n }的前n 项和为S n ，若a 3＝18，S 3＝26，则{a n }的公比q ＝________.1．等比数列的三种判定方法(1)定义：a n ＋1a n＝q (q 是不为零的常数，n ∈N *)⇔{a n }是等比数列．(2)通项公式：a n ＝cq n －1(c 、q 均是不为零的常数，n ∈N *)⇔{a n }是等比数列．(3)等比中项法：a 2n ＋1＝a n ·a n ＋2(a n ·a n ＋1·a n ＋2≠0，n ∈N *)⇔{a n }是等比数列． 2．等比数列的常见性质(1)若m ＋n ＝p ＋q ＝2k (m ，n ，p ，q ，k ∈N *)，则a m ·a n ＝a p ·a q ＝a 2k ；(2)若数列{a n }、{b n }(项数相同)是等比数列，则{λa n }、⎩⎨⎧⎭⎬⎫1a n 、{a 2n }、{a n ·b n}、⎩⎨⎧⎭⎬⎫a n bn (λ≠0)仍然是等比数列；(3)在等比数列{a n }中，等距离取出若干项也构成一个等比数列，即a n ，a n ＋k ，a n ＋2k ，a n ＋3k ，…为等比数列，公比为q k ；(4)公比不为－1的等比数列{a n }的前n 项和为S n ，则S n ，S 2n －S n ，S 3n －S 2n 仍成等比数列，其公比为q n ，当公比为－1时，S n ，S 2n －S n ，S 3n －S 2n 不一定构成等比数列． 3．求解等比数列的基本量常用的思想方法(1)方程的思想：等比数列的通项公式、前n 项和的公式中联系着五个量：a 1，q ，n ，a n ，S n ，已知其中三个量，可以通过解方程(组)求出另外两个量；其中基本量是a 1与q ，在解题中根据已知条件建立关于a 1与q 的方程或者方程组，是解题的关键．(2)分类讨论思想：在应用等比数列前n 项和公式时，必须分类求和，当q ＝1时，S n ＝na 1；当q ≠1时，S n ＝a 1(1－q n )1－q ；在判断等比数列单调性时，也必须对a 1与q 分类讨论．[练一练]1．(2010·江苏高考)函数y ＝x 2(x >0)的图像在点(a k ，a 2k )处的切线与x 轴交点的横坐标为a k ＋1，其中k ∈N *.若a 1＝16，则a 1＋a 3＋a 5的值是________．2．已知数列{a n }是公比q ≠±1的等比数列，则在{a n ＋a n ＋1}，{a n ＋1－a n }，⎩⎨⎧⎭⎬⎫a n a n ＋1，{na n }这四个数列中，是等比数列的有________个． 答案：3考点一等比数列的基本运算1.(2013·盐城三调)在等比数列{a n }中，若a 2＝－2，a 6＝－32，则a 4＝________.2．(2014·扬州模拟)已知等比数列{a n }中，公比q >1，且a 1＋a 4＝9，a 2a 3＝8，则a 2 013＋a 2 014a 2 011＋a 2 012＝________.3．设等比数列{a n}的公比q<1，前n项和为S n，已知a3＝2，S4＝5S2，求{a n}的通项公式．[类题通法]1．对于等比数列的有关计算问题，可类比等差数列问题进行，在解方程组的过程中要注意“相除”消元的方法，同时要注意整体代入(换元)思想方法的应用．2．在涉及等比数列前n项和公式时要注意对公比q是否等于1进行判断和讨论．考点二等比数列的判定与证明[典例]已知数列{a n}的前n项和为S n，且a n＋S n＝n.(1)设c n＝a n－1，求证：{c n}是等比数列；(2)求数列{a n}的通项公式．在本例条件下，若数列{b n}满足b1＝a1，b n＝a n－a n－(n≥2), 证明{b n}是等比数列.1证明一个数列为等比数列常用定义法与等比中项法，其他方法只用于选择、填空题中的判定；若证明某数列不是等比数列，则只要证明存在连续三项不成等比数列即可． [针对训练]已知数列{a n }满足：a 1＝1，a 2＝a (a ≠0)，a n ＋2＝p ·a 2n ＋1a n(其中p 为非零常数，n ∈N *)．(1)判断数列⎩⎨⎧⎭⎬⎫a n ＋1a n 是不是等比数列； (2)求a n .考点三等比数列的性质[典例] (1)(2014·苏州期末)在等比数列{a n }中，若a 3a 5a 7＝－8，则a 2a 8＝________.(2)(2014·盐城二模)若等比数列{a n }满足a m －3＝4且a m a m －4＝a 24(m ∈N *且 m >4)，则a 1a 5的值为________．等比数列常见性质的应用等比数列的性质可以分为三类：①通项公式的变形，②等比中项的变形，③前n 项和公式的变形．根据题目条件，认真分析，发现具体的变化特征即可找出解决问题的突破口． [针对训练]1．(2014·苏北四市调研)已知在等比数列{a n }中，a 1＋a 2＝12，a 3＋a 4＝1，则a 7＋a 8＋a 9＋a 10＝________.2．(2014·南京二模)已知等比数列{a n }的公比q >0，a 2＝1，a m ＋2＋a m ＋1＝6a m ，则{a n }的前4项和是________．[课堂练通考点]1．(2014·南京学情调研)已知等比数列{a n }的公比q ＝－12，S n 为其前n 项和，则S 4a 4＝________.2．(2014·连云港期末)在正项等比数列{a n }中，a 3a 11＝16，则log 2a 2＋log 2a 12＝________.3．已知等比数列{a n }的各项均为正数，且a 1＋2a 2＝3，a 24＝4a 3a 7，则数列{a n }的通项公式为________．4．已知数列{a n }是等比数列，a 1，a 2，a 3依次位于下表中第一行，第二行，第三行中的某一格内，又11。

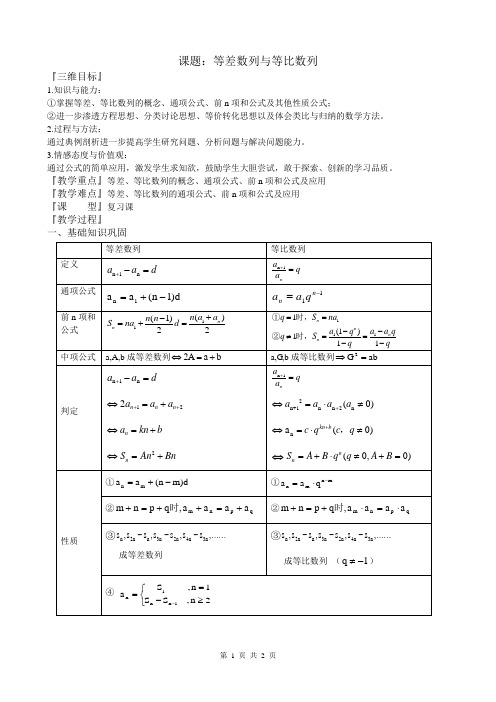
课题：等差数列与等比数列『三维目标』1.知识与能力：①掌握等差、等比数列的概念、通项公式、前n项和公式及其他性质公式；②进一步渗透方程思想、分类讨论思想、等价转化思想以及体会类比与归纳的数学方法。

2.过程与方法：通过典例剖析进一步提高学生研究问题、分析问题与解决问题能力。

3.情感态度与价值观：通过公式的简单应用，激发学生求知欲，鼓励学生大胆尝试，敢于探索、创新的学习品质。

『教学重点』等差、等比数列的概念、通项公式、前n项和公式及应用『教学难点』等差、等比数列的通项公式、前n项和公式及应用『课型』复习课『教学过程』一、基础知识巩固二、例题分析◆例1．(2011辽宁)已知等差数列{a n }满足a 2=0，a 6+a 8= -10 （I ）求数列{a n }的通项公式◇练一练(2011福建)等比数列{a n }的公比q=3，前3项和S 3=133（I ）求数列{a n }的通项公式； ◆例2．（2009北京）若数列{}n a 满足：111,2()n n a a a n N *+==∈，则5a = ；8S =◇练一练（2012合肥三模)已知数列{}n a 满足122n n n a a a ++=-（*n N ∈）2151,75a S =-=,则5a =_______◆例3. (2011浙江)已知公差不为0的等差数列{}n a 的首项1a a = (a R ∈),设数列的前n 项和为n S ，且11a ，21a ，41a 成等比数列 （I ）求数列{}n a 的通项公式及nS1.（2010重庆）在等差数列{}n a 中，1910a a +=，则5a 的值为________2.（2009湖南）设n S 是等差数列{}n a 的前n 项和，已知23a =，611a =，则7S 等于______3.（2010全国Ⅰ）已知各项均为正数的等比数列{}n a ，1235a a a =，78910a a a =，则456a a a =_______4.（2009江西）设等比数列{}n a 的前n 项和为n S ，若63S S =3，则96SS =______ 5.（2010安徽）设数列{}n a 的前n 项和2n S n =，则8a 的值为________ 1．数列{}n a 中，若满足11a =，1112n n a a +-=，则数列1n a ⎧⎫⎨⎬⎩⎭是_______数列， 数列{}n a 的通项公式n a =________2. 数列{}n a 中，若11a =，121n n a a +=+，求数列{}n a 通项公式n a三、归纳小结：等差、等比数列是数列的基础内容，也是高中数学重点内容。

高三数学《等比数列》教学设计[推荐五篇]第一篇：高三数学《等比数列》教学设计作为一名辛苦耕耘的教育工作者，通常会被要求编写教学设计，教学设计是对学业业绩问题的解决措施进行策划的过程。

教学设计应该怎么写才好呢？下面是小编为大家收集的高三数学《等比数列》教学设计，仅供参考，希望能够帮助到大家。

教学重点：理解等比数列的概念，认识等比数列是反映自然规律的重要数列模型之一，探索并掌握等比数列的通项公式。

教学难点：遇到具体问题时，抽象出数列的模型和数列的等比关系，并能用有关知识解决相应问题。

教学过程：一.复习准备1.等差数列的通项公式。

2.等差数列的前n项和公式。

3.等差数列的性质。

二.讲授新课引入：1“一尺之棰，日取其半，万世不竭。

”2细胞分裂模型3计算机病毒的传播由学生通过类比，归纳，猜想，发现等比数列的特点进而让学生通过用递推公式描述等比数列。

让学生回忆用不完全归纳法得到等差数列的通项公式的过程然后类比等比数列的通项公式注意：1公比q是任意一个常数，不仅可以是正数也可以是负数。

2当首项等于0时，数列都是0。

当公比为0时，数列也都是0。

所以首项和公比都不可以是0。

3当公比q=1时，数列是怎么样的，当公比q大于1，公比q小于1时数列是怎么样的？4以及等比数列和指数函数的`关系5是后一项比前一项。

列：1，2，（略）小结：等比数列的通项公式三.巩固练习：1.教材P59练习1，2，3，题2.作业：P60习题1，4。

第二课时5.2.4等比数列（二）教学重点：等比数列的性质教学难点：等比数列的通项公式的应用一.复习准备：提问：等差数列的通项公式等比数列的通项公式等差数列的性质二.讲授新课：1.讨论：如果是等差列的三项满足那么如果是等比数列又会有什么性质呢？由学生给出如果是等比数列满足2练习：如果等比数列=4，=16，=？(学生口答)如果等比数列=4，=16，=？(学生口答)3等比中项：如果等比数列.那么，则叫做等比数列的等比中项（教师给出）4思考：是否成立呢？成立吗？成立吗？又学生找到其间的规律，并对比记忆如果等差列，5思考：如果是两个等比数列，那么是等比数列吗？如果是为什么？是等比数列吗？引导学生证明。

等比数列教学案篇一：等比数列第一课时教案等比数列的定义教案内容：等比数列教学目标:1.理解和掌握等比数列的定义；2.理解和掌握等比数列的通项公式及其推导过程和方法；3.运用等比数列的通项公式解决一些简单的问题。

授课类型：课时安排：1教学重点：等比数列定义、通项公式的探求及运用。

教学难点：等比数列通项公式的探求。

教具准备：多媒体课件教学过程：（一）复习导入1．等差数列的定义2．等差数列的通项公式及其推导方法3.公差的确定方法.4.问题：给出一张书写纸，你能将它对折10次吗？为什么？（二）探索新知1．引入：观察下面几个数列，看其有何共同特点？（１）－2，1，4，7，10，13，16，19，（２）8，16，32，64，128，256，（３）1，1，1，1，1，1，1，（４）1，2，4，8，16，263请学生说出数列上述数列的特性，教师指出实际生活中也有许多类似的例子，如细胞分裂问题.假设每经过一个单位时间每个细胞都分裂为两个细胞，再假设开始有一个细胞，经过一个单位时间它分裂为两个细胞，经过两个单位时间就有了四个细胞，，一直进行下去，记录下每个单位时间的细胞个数得到了一列数这个数列也具有前面的几个数列的共同特性，这就是我们将要研究的另一类数列——等比数列.2．等比数列定义：一般地，如果一个数列从第二项起，每一项与它的前一．．．．项的比等于同一个常数，那么这个数列就叫做等比数列，这个常数叫做等比数列．．的公比；公比通常用字母q表示(q0)，3.递推公式：an1∶anq(q0)对定义再引导学生讨论并强调以下问题（1）等比数列的首项不为0；（2）等比数列的每一项都不为0；（3）公比不为0.（4）非零常数列既是等比数列也是等差数列；问题：一个数列各项均不为0是这个数列为等比数列的什么条件？3．等比数列的通项公式：【傻儿子的故事】古时候,有一个人不识字,他不希望儿子也像他这样,他就请了个教书先生来教他儿子认字，他儿子见老师第一天写“一”就是一划，第二天“二”就是二划，第三天“三”就是三划,他就跑去跟他父亲说:“爸爸,我会写字了,请你叫老师走吧!”这人听了很高兴,就给老师结算了工钱叫他走了。

等比数列教案等比数列教案篇一一、概述教材内容：等比数列的概念和通项公式的推导及简单应用教材难点：灵活应用等比数列及通项公式解决一般问题教材重点：等比数列的概念和通项公式二、教学目标分析1、知识目标掌握等比数列的定义理解等比数列的通项公式及其推导2．能力目标(1）学会通过实例归纳概念(2）通过学习等比数列的通项公式及其推导学会归纳假设(3）提高数学建模的能力3、情感目标：(1）充分感受数列是反映现实生活的模型(2）体会数学是来源于现实生活并应用于现实生活(3）数学是丰富多彩的而不是枯燥无味的三、教学对象及学习需要分析1、教学对象分析：(1）高中生已经有一定的学习能力，对各方面的知识有一定的基础，理解能力较强。

并掌握了函数及个别特殊函数的性质及图像，如指数函数。

之前也刚学习了等差数列，在学习这一章节时可联系以前所学的进行引导教学。

(2）对归纳假设较弱，应加强这方面教学2、学习需要分析：四。

教学策略选择与设计1、课前复习(1）复习等差数列的概念及通向公式(2）复习指数函数及其图像和性质2．情景导入等比数列教案篇二【教学目标】知识目标：正确理解等比数列的定义，了解公比的概念，明确一个数列是等比数列的限定条件，能根据定义判断一个数列是等比数列，了解等比数列在生活中的应用。

能力目标：通过对等比数列概念的归纳，培养学生严密的思维习惯；通过对等比数列的研究，逐步培养学生观察、类比、归纳、猜想等思维能力并进一步培养学生善于思考，解决问题的能力。

情感目标：培养学生勇于探索、善于猜想的学习态度，实事求是的科学态度，调动学生的积极情感，主动参与学习，感受数学文化。

【教学重点】等比数列定义的归纳及运用。

【教学难点】正确理解等比数列的定义，根据定义判断或证明某些数列是否为等比数列【教学手段】多媒体辅助教学【教学方法】启发式和讨论式相结合，类比教学。

【课前准备】制作多媒体课件，准备一张白纸，游标卡尺。

【教学过程】复习回顾：等差数列的定义。

等比数列一轮复习教学设计教学设计：等比数列一轮复习一、教学目标：1. 复习等比数列的概念和性质；2. 复习等比数列的通项公式和求和公式；3. 能够应用等比数列的知识解决实际问题。

二、教学内容与方法：1. 概念和性质的复习（1）复习等比数列的定义：若一个数列中，从第二项起，每一项与其前一项的比都相等，那么这个数列就是等比数列。

（2）复习等比数列的通项公式和求和公式。

（3）通过练习题巩固概念和性质的理解。

2. 应用题的解决方法（1）通过实际问题引入等比数列的应用，如利息问题、人口增长问题等。

（2）分析问题，找到规律，建立等比数列模型。

（3）利用等比数列的性质和公式求解问题，注意理解问题的实际意义。

（4）通过练习题巩固应用题的解题方法。

三、教学流程：1. 复习概念和性质（1）导入：通过提问、展示实际问题引入等比数列的概念。

（2）复习等比数列的定义和性质，包括公比与比例关系、前n项和公式等。

（3）例题演示和讲解，帮助学生理解等比数列的概念和性质。

（4）通过练习题让学生巩固概念和性质的理解。

2. 复习通项公式和求和公式（1）复习等比数列的通项公式和求和公式。

（2）例题演示和讲解，帮助学生掌握通项公式和求和公式的使用。

（3）通过练习题让学生巩固通项公式和求和公式的运用。

3. 应用题的解决方法（1）导入：通过提问、展示实际问题引入等比数列的应用。

（2）分析问题，找到规律，建立等比数列模型。

（3）利用等比数列的性质和公式求解问题，并注意理解问题的实际意义。

（4）通过练习题让学生巩固应用题的解题方法。

4. 综合练习（1）通过综合练习题复习等比数列的知识点和解题方法。

（2）有难度的问题进行讲解和解答。

四、教学资源准备：1. 教材：配套教材的相关内容；2. 课件：概念、性质、公式的讲解与演示；3. 练习题：根据难易程度准备一些练习题。

五、教学评价方式：1. 课堂讨论与提问；2. 学生完成的练习题和应用题答案；3. 学生的思维能力和解题思路的表现。

高三数学复习课学案 课题 等比数列 课型 复习课教学目标1、 理解等比数列的概念2、 掌握等比数列的通项公式及其推导方法，并能用通项公式解决一些简单问题。

3、 掌握等比数列的前n 项和公式及其推导方法，并能用前n 项和公式解决一些简单问题。

4、 掌握等比数列的概念及其应用。

教学方法讲授法、讨论法 教具 投影仪、多媒体 教学过程 一、 考点分析：等比数列的定义、判定、通项公式和前n 项和公式的探求，等比数列性质的应用是历年高考的必考内容，题型既有客观题又有解答题，难度低、中、高，客观题突出“小而巧”，主观题都为“大而全”，常与等差数列，函数、方程、解几等有关知识综合。

二、研究问题：⎪⎪⎩⎪⎪⎨⎧性质项和前通项公式定义n 等比数列三、 教学过程：（一 ) 基础题型检测1、 是ａ、ｘ、ｂ成等比数列的（ ）条件A ．充分不必要 B.必要不充分C ．充要条件 D.既不充分又不必要2、等比数列｛a n ｝中，a 3=3, a 10=384,则｛a n ｝的通项公式是________________ ab X =3、｛a n｝是等比数列，且a n>0,a2a4+2a3a5+a4a6=25，则a3+a5=______________4、设等比数列｛a n｝的前n项和为S n，S3+S6=2S9则｛a n｝的公比是_________5、等比数列｛a n｝的前n项和为S n=3n+a，则a等于__________6、在等比数列｛a n｝中，S n=a1+a2+…+a n,若S10=5, S20=15，则S30=____________（二）典型例题：例1：有四个数，其中前三个数成等差数列，后三个数成等比数列，且第一个数与第四个数的和是16，第二个的数与第三个数的和是12，求此四数例2：数列｛a n｝为正项等比数列，它的前n项和为80,其中数值最大的项是54，前2n项的和为6560，求首项a1和公比q例3：已知数列｛a n｝的前n项和为S n=2a n+1求证：｛a n｝是等比数列，并求其通项公式（三）课堂反馈1、（04年）等比数列｛a n ｝中，a 2=9, a 5=243,则,S 4为________A.81B.120C.168D.1922、在等比数列｛a n ｝中，存在正整数m,有a m =3,a m+5=24,则a m+15=_______A.864B.1176C.1440D.15363、已知数列｛a n ｝为等差数列，｛b n ｝为等比数列，其公比q ≠1，且b n ＞0，若a 1=b 1,a 11=b 11,则——A. a 6=b 6B.a 6＞b 6 C a 6<b 6 D 不确定4、等比数列｛a n ｝中，已知a 3a 4a 5=8，则a 2a 3a 4a 5a 6=______________5、等差数列｛a n ｝中，公差d ≠0,若a 1，a 3，a 9成等差数列，则 =________________6、已知数列｛a n ｝的前n 项和为S n ，S n =2（a n －1）(n ∈N ＊)，若｛a n ｝中的最大项为128，求n7、设数列｛a n ｝的前n 项和为S n =aq n +b(a 、b 为非零实数，q ≠0, q ≠1)⑴a 、b 满足什么关系时，数列｛a n ｝为等比数列⑵若｛a n ｝为等比数列，证明以（a n ,S n ）为坐标的点都落在同一条直线上四、思想方法总结 1042931a a a a a a ++++1．方程思想：在等比数列中，由通项公式、求和公式建立方程，根据a 1，q ，n ，a n ，S n 中的任意三个量求出其余的两个量。

等比数列教案教学目标：（1）掌握等比数列的定义；归纳出等比数列的通项公式。

（2）通过实例，理解等比数列的概念；探索并掌握等比数列的通项公式、性质，能在具体的问题情境中，发现数列的等比关系，提高数学建模能力；会解决关于等比数列的简单问题。

（3）进行史志教育，激发学生学习的学习兴趣；渗透数学中的类比、归纳、猜测等合情推理方法；充分感受数列是反映现实生活的模型，体会数学是来源于现实生活，并应用于现实生活的，数学是丰富多彩的而不是枯燥无味的。

重难点：等比数列的定义及通项公式、性质。

教学重点：灵活应用定义式及通项公式、性质解决相关问题。

教学过程：1、复习导入：（1）等差数列的定义：如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，这个数列就叫做等差数列，这个常数叫做等差数列的公差，通常用d来表示。

（2）等差数列的通项公式：An=A1+(n-1)d（3）An=Am+(n-m)d (n>m)（4）若m+n=p+q,则Am+An=Ap+Aq.2、引入：早在春秋战国时代，我国名家公孙子龙就有个著名论断：“一尺之锤，日取其半，万世不竭。

”（用粉笔在手中演练）若设该锤的单位长度为1，则每天所得的长度构成一个数列：1/2,1/4,1/8，1/16……在此引入数学史料，进行数学史志教育。

在印度有这样一个美妙的传说，印度国王为了嘉奖国际象棋的发明者，将他召到王宫，并让他尽管提条件，这个发明者说：“请国王在国际象棋棋盘的第1个格子里放上1粒麦子，第2个格子里放上2粒麦子，第3个格子里放上4粒麦子，第4个格子里放上8粒麦子，以此类推，直到最后一个格子。

国王听后哈哈大笑，说他条件太少了，便吩咐人去办，可经办人一算，吓了一跳，发现全印度的麦子给了他还远远不够。

那在这里呢，毎格的麦子数构成了这样一个数列：1,2,4,8,……由此激发学生的学习兴趣。

3、定义：在认真考察以上两个数列，寻求他们的共同点，并对照等差数列的定义，绝大部分同学都非常轻松地自己给出等比数列的定义。

第三节等比数列课程标准1.理解等比数列的概念并掌握其通项公式与前n项和公式.2.能在具体的问题情境中,发现数列的等比关系,并解决相应的问题.3.体会等比数列与指数函数的关系.考情分析考点考法:高考命题常以等比数列为载体,考查基本量的运算、求和及性质的应用.等差数列与等比数列的综合应用是高考的热点,在各个题型中均有出现.核心素养:数学建模、数学运算、逻辑推理.【必备知识·逐点夯实】【知识梳理·归纳】1.等比数列的有关概念定义一般地,如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数(不为零),那么这个数列叫做等比数列通项公式设{a n}是首项为a1,公比为q的等比数列,则通项公式a n=a1q n-1.推广:a n=a m q n-m(m,n∈N*)等比中项如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项.此时,G2=ab【微点拨】(1)等比数列中不含有0项;(2)同号的两个数才有等比中项,且等比中项有两个,它们互为相反数.2.等比数列的前n项和公式【微点拨】在运用等比数列的前n项和公式时,必须注意对q=1与q≠1分类讨论,防止因忽略q=1这一特殊情形而导致解题失误.3.等比数列与指数函数的关系等比数列的通项公式可整理为a n=1·q n,而y=1·q x(q≠1)是一个不为0的常数1与指数函数q x的乘积,从图象上看,表示数列1·q n中的各项的点是函数y=1·q x的图象上孤立的点.4.等比数列的性质(1)对任意的正整数m,n,p,q,若m+n=p+q,则a m·a n=a p·a q.特别地,若m+n=2p,则a m·a n=2.(2)若等比数列前n项和为S n,则S m,S2m-S m,S3m-S2m仍成等比数列(公比q≠-1).(3)数列{a n}是等比数列,则数列{pa n}(p≠0,p是常数)也是等比数列.(4)在等比数列{a n}中,等距离取出若干项也构成一个等比数列,即a n,a n+k,a n+2k,a n+3k,…为等比数列,公比为q k.(5)等比数列{a n}的单调性:当q>1,a1>0或0<q<1,a1<0时,数列{a n}是递增数列;当q>1,a1<0或0<q<1,a1>0时,数列{a n}是递减数列;当q=1时,数列{a n}是常数列.【基础小题·自测】类型辨析改编易错高考题号12341.(多维辨析)(多选题)下列结论正确的是()A.满足a n+1=qa n(n∈N*,q为常数)的数列{a n}为等比数列B.三个数a,b,c成等比数列的必要不充分条件是b2=acC.数列{a n}的通项公式是a n=a n,则其前n项和为S n=(1-)1-D.如果数列{a n}为正项等比数列,则数列{ln a n}是等差数列【解析】选BD.A中q不能为0;B中当a=b=c=0时满足b2=ac,但不是等比数列;C 中a=1时不成立;D中,a n>0,设a n=a1q n-1,则ln a n=ln a1+(n-1)ln q,{ln a n}是等差数列.2.(选择性必修第二册P29例1·变形式)若{a n}是各项均为正数的等比数列,且a1=1,a5=16,则a6-a5=()A.32B.-48C.16D.-48或16【解析】选C.由题意,q>0,则q=2,所以a6-a5=a5(q-1)=16.3.(忽视前n项和的条件致误)等比数列{a n}中,a3=6,前三项和S3=18,则公比q的值为()A.1B.-12C.1或-12D.-1或-12【解析】选C.因为S3=18,a3=6,所以a1+a2=32(1+q)=12,故2q2-q-1=0,解得q=1或q=-12.4.(2023·全国乙卷)已知{a n}为等比数列,a2a4a5=a3a6,a9a10=-8,则a7=________.【解析】设{a n}的公比为q(q≠0),则a2a4a5=a3a6=a2q·a5q,显然a n≠0,则a4=q2,即a1q3=q2,则a1q=1.因为a9a10=-8,则a1q8·a1q9=-8,则q15=(5)3=-8=(-2)3,则q5=-2,则a7=a1q·q5=q5=-2.答案:-2【巧记结论·速算】1.若{a n},{b n}(项数相同)是等比数列,则{λa n}(λ≠0),{1},{2},{a n·b n数列.2.当{a n}是等比数列且q≠1时,S n=11--11-·q n=A-A·q n.【即时练】1.设n∈N*,则“数列{a n}为等比数列”是“”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【解析】选A.充分性:若数列为等比数列,公比为q,为公比为12的等比数列,充分性成立;必要性:,公比为q,则-1=±所以数列不是等比数列,必要性不成立.2.已知数列{a n}的前n项和S n=22n+1+a,若此数列为等比数列,则a=________.【解析】因为数列的前n项和S n=22n+1+a=2×4n+a,所以a=-2.答案:-2【核心考点·分类突破】考点一等比数列基本量的计算[例1](1)(一题多法)记S n为等比数列{a n}的前n项和,若a5-a3=12,a6-a4=24,则=()A.2n-1B.2-21-nC.2-2n-1D.21-n-1【解析】选B.方法一:设等比数列{a n}的公比为q,则由5-3=14-12=12,6-4=15-13=24,解得1=1,=2,所以S n=1(1-)1-=2n-1,a n=a1q n-1=2n-1,所以=2-12-1=2-21-n.方法二:设等比数列{a n}的公比为q,因为6-45-3=4(1-2)3(1-2)=43=2412=2,所以q=2,所以=1(1-)1-1-1=2-12-1=2-21-n.(2)已知等比数列{a n}的前n项和为S n,若a3a11=232,且S8+S24=mS16,则m=()A.-4B.4C.-83D.83【解析】选D.因为a3a11=232,且a n≠0,所以a11=2a3即a1q10=2a1q2,解得q8=2或q=0(舍去),因为S 8+S 24=mS 16,所以1(1-8)1-+1(1-24)1-=m ·1(1-16)1-,又因为q 8=2,a 1≠0,所以-8=-3m ,解得m =83.【解题技法】等比数列基本量的计算(1)等比数列中有五个量a 1,n ,q ,a n ,S n ,一般可以“知三求二”,通过列方程(组)求解;(2)注意观察条件转化式的特点,尽量采用整体消元、代入的方法简化运算,如两式相除就是等比数列中常用的运算技巧.【对点训练】1.已知各项均为正数的等比数列{a n }的前4项和为15,且a 5=3a 3+4a 1,则a 3=()A .16B .8C .4D .2【解析】选C .设各项均为正数的等比数列{a n }的公比为q ,则1+1+12+13=15,14=312+41,解得1=1=2,所以a 3=a1q 2=4.2.已知{a n }是首项为1的等比数列,S n 是{a n }的前n 项和,且9S 3=S 6,5项和为()A .158或5B .3116或5C .3116D .158【解析】选C .若q =1,则由9S 3=S 6,得9×3a 1=6a 1,则a 1=0,不满足题意,故q ≠1.由9S 3=S 6,得9×1(1-3)1-=1(1-6)1-,解得q =2.故a n =a 1q n-1=2n -1,1=(12)n -1.1为首项,以12为公比的等比数列,所以5项和为T 5=1×[1-(12)5]1-12=3116.【加练备选】设公比为q(q>0)的等比数列{a n}的前n项和为S n.若S2=3a2+2,S4=3a4+2,则q=()A.32B.12C.23D.2【解析】选A.因为在等比数列中,S2=3a2+2,S4=3a4+2,所以S4-S2=a3+a4=3(a4-a2),所以a2(q+q2)=3a2(q2-1),又a2≠0,所以q+q2=3(q2-1),即2q2-q-3=0,又q>0,所以q=32.考点二等比数列的判定与证明[例2]已知数列{a n}中,a1=1且2a n+1=6a n+2n-1(n∈N*),(1)求证:数列+;(2)求数列{a n}的通项公式.【解析】(1)因为2a n+1=6a n+2n-1(n∈N*),所以a n+1=3a n+n-12,所以r1+r12+2=3+-12+r12+2=3+32+2=3,因为a1+12=1+12=32,所以数列+2是首项为32,公比为3的等比数列.(2)由(1)得,a n+2=32×3n-1=12×3n,所以a n=12×3n-2.【解题技法】等比数列的判定方法定义法若a n+1a n=q(q为非零常数,n∈N*)或-1=q(q为非零常数且n≥2,n∈N*),则{a n}是等比数列等比中项法若数列{a n}中,a n≠0且r12=a n·+2(n∈N*),则{a n}是等比数列【对点训练】数列{a n}中,a1=2,a n+1=r12a n(n∈N*).证明数列{}是等比数列,并求数列{a n}的通项公式.【解析】由题设得r1r1=12·,又11=2,所以数列{}是首项为2,公比为12的等比数列,所以=2×(12)n-1=22-n,a n=n·22-n=42.【加练备选】成等差数列的三个正数的和等于15,并且这三个数分别加上2,5,13后成为等比数列{b n}中的b3,b4,b5.(1)求数列{b n}的通项公式;(2)数列{b n}的前n项和为S n,求证:数列{S n+54}是等比数列.【解析】(1)设成等差数列的三个正数分别为a-d,a,a+d,依题意,得a-d+a+a+d=15,解得a=5.所以数列中的b3,b4,b5依次为7-d,10,18+d.依题意,有(7-d)(18+d)=100,解得d=2或d=-13(舍去),故数列的第3项为5,公比为2.由b 3=b 1·22,即5=b 1·22,解得b 1=54.所以数列是以54为首项,以2为公比的等比数列,其通项公式为b n =54·2n -1=5·2n -3.(2)数列的前n 项和S n =54(1-2)1-2=5·2n -2-54,即S n +54=5·2n -2,所以S 1+54=52,r1+54+54=5·2-15·2-2=2.因此{S n +54}是以52为首项,以2为公比的等比数列.考点三等比数列性质的应用【考情提示】等比数列的性质作为解决等比数列问题的工具,因其考查数列知识较全面而成为高考命题的热点,重点解决基本量运算、条件转化等.角度1等比数列项的性质[例3]已知各项均为正数的等比数列的前n 项和为S n ,a 2a 4=9,9S 4=10S 2,则a 2+a 4的值为()A .30B .10C .9D .6【解析】选B .已知为各项均为正数的等比数列,则a n >0,可得a 1>0,q >0,因为32=a 2a 4=9,所以a 3=3,又因为9S 4=10S 2,则9(a 1+a 2+a 3+a 4)=10(a 1+a 2),可得9(a 3+a 4)=a 1+a 2,所以3+41+2=q 2=19,解得q =13,故a 2+a 4=3+a 3q =10.角度2等比数列前n 项和的性质[例4]已知正项等比数列{a n}的前n项和为S n,且S8-2S4=5,则a9+a10+a11+a12的最小值为()A.10B.15C.20D.25【解析】选C.由题意可得a9+a10+a11+a12=S12-S8,由S8-2S4=5,可得S8-S4=S4+5.又由等比数列的性质知S4,S8-S4,S12-S8成等比数列,则S4(S12-S8)=(S8-S4)2.于是a9+a10+a11+a12=S12-S8=(4+5)24=S4+254+10≥2当且仅当S4=5时等号成立.所以a9+a10+a11+a12的最小值为20.角度3等比数列的单调性[例5]已知{a n}是等比数列,a1>0,前n项和为S n,则“2S8<S7+S9”是“{a n}为递增数列”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解析】选B.因为数列是等比数列,a1>0,2S8<S7+S9,所以a8<a9,所以q7<q8,所以q7(q-1)>0,所以q<0或q>1,所以2S8<S7+S9的充要条件为q<0或q>1.又a1>0,数列为递增数列的充要条件为q>1,所以“2S8<S7+S9”是“为递增数列”的必要不充分条件.【解题技法】1.应用等比数列性质的两个关注点(1)转化意识:在等比数列中,两项之积可转化为另外两项之积或某项的平方,这是最常用的性质.(2)化归意识:把非等比数列问题转化为等比数列问题解决,例如有关S m,S2m,S3m的问题可利用S m,S2m-S m,S3m-S2m(S m≠0)成等比数列求解.2.等比数列的单调性的应用方法研究等比数列的单调性问题,要综合考虑首项的符号以及公比的取值范围,而涉及等比数列有关的单调性的充分必要条件问题,既要考虑数列的单调性也要善于举反例说明.【对点训练】1.设单调递增的等比数列{a n}满足12+14=1336,a1a5=36,则公比q=()A.32B.94C.2D.52【解析】选A.因为数列{a n}为等比数列,所以a1a5=a2a4=36,所以12+14=2+424=2+436=1336,则a2+a4=13,又数列{a n}单调递增,所以q>1,解得a2=4,a4=9,则q2=94,因为q>1,所以q=32.2.设无穷等比数列{a n}的前n项和为S n,若-a1<a2<a1,则()A.{S n}为递减数列B.{S n}为递增数列C.数列{S n}有最大项D.数列{S n}有最小项【解析】选D.由-a1<a2<a1可得a1>0,所以q=21<1,因为-a1<a2得q=21>-1,所以-1<q<1,因为S n=1(1-)1-,当0<q<1时,{S n}递增,当-1<q<0时,{S n}既有递增又有递减,A,B错误;当0<q<1时,S n有最小项S1,没有最大项,当-1<q<0时,a1>0,a2<0,a3>0,a4<0且a3+a4>0,S n有最小项S2,没有最大项,C错误,D 正确.3.设等比数列{a n}的前n项和为S n.若a n>0,S3=5,a7+a8+a9=20,则S15=________.【解析】由等比数列的性质可知S3,S6-S3,S9-S6,S12-S9,S15-S12是等比数列,由条件可知S3=5,S9-S6=20,则此等比数列的公比q2=205=4,又a n>0,所以q=2,S15=S3+(S6-S3)+(S9-S6)+(S12-S9)+(S15-S12),所以S15=5(1-25)1-2=155.答案:155。