2018届高三数学每天一练半小时第29练 正弦定理、余弦定理 Word版含答案

2018届高考数学正弦定理、余弦定理的应用复习题及答案
5 c 高三数学（理）一轮复习教案第五编平面向量、解三角形总第25期
§55 正弦定理、余弦定理的应用
基础自测
1在某次测量中，在A处测得同一半平面方向的B点的仰角是60°,c点的俯角为70°，则∠BAc=
答案130°
2从A处望B处的仰角为，从B处望A处的俯角为，则、的大小关系为
答案 =
3在△ABc中，若(a+b+c)(a+b-c)=3ab,且sinc=2sinAcsB,则△ABc是三角形
答案等边
4已知A、B两地的距离为10 ,B、c两地的距离为 =5，
∴AB= ()∴A、B之间的距离为
例2．沿一条小路前进，从A到B，方位角（从正北方向顺时针转到AB方向所成的角）是50°，距离是3 ，从B到c方位角是110°，距离是3 ，从c到D,方位角是140°，距离是（9+3 ）试画出示意图，并计算出从A到D的方位角和距离（结果保留根号）解示意图如图所示，连接Ac，在△ABc中，
∠ABc=50°+(180°-110°)=1(70°+30°)=14cs
∴=S△Pc+S△PcD= ×1×2sin + （5-4cs ）=2sin( - )+
∴当 - = ，即 = 时，ax=2+
所以四边形PDc面积的最大值为2+
巩固练习
1某观测站c在A城的南偏西60°)=sin cs60°-cs sin60°。

课时达标检测（二十四） 正弦定理和余弦定理[练基础小题——强化运算能力]1．在△ABC 中，若sin A a ＝cos Bb，则B 的值为( ) A ．30° B ．45° C ．60°D ．90°解析：选B 由正弦定理知，sin A sin A ＝cos Bsin B，∴sin B ＝cos B ，∴B ＝45°.2．在△ABC 中，已知AB ＝3，A ＝120°，且△ABC 的面积为1534，则BC ＝( )A ．3B ．5C ．7D ．15解析：选C 由S △ABC ＝1534得12×3×AC sin 120°＝1534，所以AC ＝5，因此BC 2＝AB 2＋AC 2－2AB ·AC ·cos 120°＝9＋25＋2×3×5×12＝49，解得BC ＝7.3．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若a sin A ＋b sin B <c sin C ，则△ABC 的形状是( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不确定解析：选C 根据正弦定理可得a 2＋b 2<c 2.由余弦定理得cos C ＝a 2＋b 2－c 22ab <0，故C 是钝角．即△ABC 是钝角三角形．4．已知在△ABC 中，sin A ∶sin B ∶sin C ＝3∶5∶7，那么这个三角形的最大内角的大小为________．解析：由sin A ∶sin B ∶sin C ＝3∶5∶7知，三角形的三边之比a ∶b ∶c ＝3∶5∶7，最大的角为C .由余弦定理得cos C ＝－12，∴C ＝120°.答案：120°5．在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c .已知△ABC 的面积为315，b －c ＝2，cos A ＝－14，则a 的值为________．解析：在△ABC 中，由cos A ＝－14可得sin A ＝154，所以有⎩⎨⎧12bc ×154＝315，b －c ＝2，a 2＝b 2＋c 2－2bc ×⎝⎛⎭⎫－14，解得⎩⎪⎨⎪⎧a ＝8，b ＝6，c ＝4.答案：8[练常考题点——检验高考能力]一、选择题 1．在△ABC 中，若sin C sin A ＝3，b 2－a 2＝52ac ，则cos B 的值为( ) A.13 B.12 C.15 D.14解析：选D 由题意知，c ＝3a ，b 2－a 2＝52ac ＝c 2－2ac cos B ，所以cos B ＝c 2－52ac2ac ＝9a 2－152a 26a 2＝14. 2．在△ABC 中，三内角A ，B ，C 的对边分别为a ，b ，c ，面积为S ，若S ＋a 2＝(b ＋c )2，则cos A 等于( )A.45B ．－45 C.1517 D ．－1517解析：选D 由S ＋a 2＝(b ＋c )2，得a 2＝b 2＋c 2－2bc 14sin A －1，由余弦定理可得14sin A－1＝cos A ，结合sin 2A ＋cos 2A ＝1，可得cos A ＝－1517或cos A ＝－1(舍去)． 3．在△ABC 中，已知b ＝40，c ＝20，C ＝60°，则此三角形的解的情况是( ) A ．有一解 B ．有两解C ．无解D ．有解但解的个数不确定解析：选C 由正弦定理得b sin B ＝c sin C， ∴sin B ＝b sin Cc＝40×3220＝3>1.∴角B 不存在，即满足条件的三角形不存在．4．已知△ABC 中，内角A ，B ，C 所对边长分别为a ，b ，c ，若A ＝π3，b ＝2a cos B ，c＝1，则△ABC 的面积等于( )A.32 B.34 C.36 D.38解析：选B 由正弦定理得sin B ＝2sin A cos B ，故tan B ＝2sin A ＝2sin π3＝3，又B ∈(0，π)，所以B ＝π3，又A ＝π3＝B ，则△ABC 是正三角形，所以S △ABC ＝12bc sin A ＝12×1×1×32＝34.5．(2017·渭南模拟)在△ABC 中，若a 2－b 2＝3bc 且sin (A ＋B )sin B＝23，则A ＝( )A.π6B.π3C.2π3D.5π6解析：选A 因为sin (A ＋B )sin B ＝23，故sin C sin B ＝23，即c ＝23b ，则cos A ＝b 2＋c 2－a 22bc ＝12b 2－3bc 43b 2＝6b 243b2＝32，所以A ＝π6. 6．已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且c －b c －a ＝sin Asin C ＋sin B，则B ＝( )A.π6B.π4C.π3D.3π4 解析：选C 根据正弦定理a sin A ＝b sin B ＝c sin C ＝2R ，得c －b c －a ＝sin A sin C ＋sin B ＝ac ＋b，即a 2＋c 2－b 2＝ac ，所以cos B ＝a 2＋c 2－b 22ac ＝12，故B ＝π3.二、填空题7．在△ABC 中，角A ，B ，C 所对的边分别是a ，b ，c ，若c ＝1，B ＝45°，cos A ＝35，则b ＝________.解析：因为cos A ＝35，所以sin A ＝1－cos 2A ＝1－⎝⎛⎭⎫352＝45，所以sin C ＝sin[180°－(A ＋B )]＝sin(A ＋B )＝sin A cos B ＋cos A sin B ＝45cos 45°＋35sin 45°＝7210.由正弦定理b sin B ＝c sin C ，得b ＝17210×sin 45°＝57. 答案：578．在△ABC 中，若b ＝2，A ＝120°，三角形的面积S ＝3，则三角形外接圆的半径为________．解析：由面积公式，得S ＝12bc sin A ，代入数据得c ＝2，由余弦定理得a 2＝b 2＋c 2－2bc cosA ＝22＋22－2×2×2cos 120°＝12，故a ＝23，由正弦定理，得2R ＝a sin A ＝2332，解得R＝2.答案：29．在△ABC 中，a ＝4，b ＝5，c ＝6，则sin 2Asin C＝________. 解析：由正弦定理得sin A sin C ＝ac ，由余弦定理得cos A ＝b 2＋c 2－a 22bc，∵a ＝4，b ＝5，c ＝6，∴sin 2A sin C ＝2sin A cos A sin C ＝2·sin A sin C ·cos A ＝2×a c ×b 2＋c 2－a 22bc ＝2×46×52＋62－422×5×6＝1.答案：110．在△ABC 中，B ＝120°，AB ＝2，A 的角平分线AD ＝3，则AC ＝________.解析：如图，在△ABD 中，由正弦定理，得AD sin B ＝ABsin ∠ADB ，∴sin ∠ADB ＝22. 由题意知0°<∠ADB <60°，∴∠ADB ＝45°，∴∠BAD ＝180°－45°－120°＝15°.∴∠BAC ＝30°，C ＝30°，∴BC ＝AB ＝ 2.在△ABC 中，由正弦定理，得ACsin B＝BCsin ∠BAC，∴AC ＝ 6.答案： 6 三、解答题11．(2017·河北三市联考)在△ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，且a sin B ＝－b sin ⎝⎛⎭⎫A ＋π3. (1)求A ；(2)若△ABC 的面积S ＝34c 2，求sin C 的值． 解：(1)∵a sin B ＝－b sin ⎝⎛⎭⎫A ＋π3， ∴由正弦定理得sin A sin B ＝－sin B sin ⎝⎛⎭⎫A ＋π3，则sin A ＝－sin ⎝⎛⎭⎫A ＋π3，即sin A ＝－12sin A －32cos A ，化简得tan A ＝－33，∵A ∈(0，π)，∴A ＝5π6. (2)∵A ＝5π6，∴sin A ＝12，由S ＝12bc sin A ＝14bc ＝34c 2，得b ＝3c ，∴a 2＝b 2＋c 2－2bc cos A ＝7c 2，则a ＝7c ，由正弦定理得sin C ＝c sin A a ＝714. 12．(2017·郑州模拟)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且满足cos 2C －cos 2A ＝2sin ⎝⎛⎭⎫π3＋C ·sin ⎝⎛⎭⎫π3－C . (1)求角A 的值；(2)若a ＝3且b ≥a ，求2b －c 的取值范围．解：(1)由已知得2sin 2A －2sin 2C ＝234cos 2C －14sin 2C ，化简得sin A ＝32，故A ＝π3或2π3.(2)由题知，若b ≥a ，则A ＝π3，又a ＝3，所以由正弦定理可得b sin B ＝c sin C ＝asin A＝2，得b ＝2sin B ，c ＝2sin C ，故2b －c ＝4sin B －2sin C ＝4sin B －2sin ⎝⎛⎭⎫2π3－B ＝3sin B －3cos B ＝23sin ⎝⎛⎭⎫B －π6. 因为b ≥a ，所以π3≤B ＜2π3，π6≤B －π6＜π2，所以23sin ⎝⎛⎭⎫B －π6∈[3，23)．即2b －c 的取值范围为[3，23).。

第讲 正弦定理与余弦定理
．正弦定理和余弦定理
.三角形中常用的面积公式 ()＝(表示边上的高)； ()＝ ＝＝ ； ()＝，其中＝(＋＋)．
．辨明两个易误点
()在利用正弦定理解已知三角形的两边和其中一边的对角求另一边的对角，进而求出其他的边和角时，有时可能出现一解、两解或无解，所以要注意分类讨论．
()在判断三角形形状时，等式两边一般不要约去公因式，应移项提取公因式，以免漏解． ．余弦定理的推导过程 如图，设＝，＝， ＝.
则＝－，
所以＝(－)
＝－·＋
＝＋－ .
即＝＋－.
同理可证＝＋－ .
＝＋－ .
．三角形解的判断
在△中，＝°，＝°，＝，则等于( )
．．
．．
由正弦定理得)＝)，
所以＝° °)＝＝.
在△中，已知＝，＝，＝，则＋＝( ) ．°．°
．°．°
＝＝＝.
所以＝°，所以＋＝°.
．在△中，若＝，＝，＝°，则此三角形( ) ．无解．有两解
．有一解．解的个数不确定因为)＝)，
所以＝·＝×°。

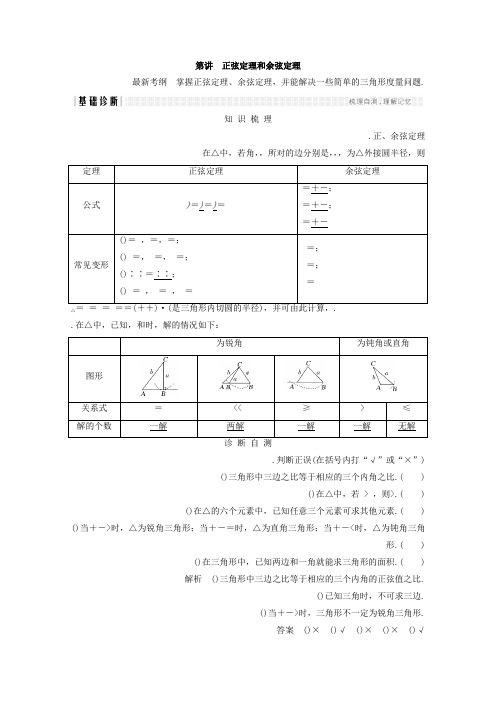
第讲正弦定理和余弦定理最新考纲掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题.知识梳理.正、余弦定理在△中，若角，，所对的边分别是，，，为△外接圆半径，则△.在△中，已知，和时，解的情况如下：.判断正误(在括号内打“√”或“×”)()三角形中三边之比等于相应的三个内角之比.( )()在△中，若 > ，则>.( )()在△的六个元素中，已知任意三个元素可求其他元素.( ) ()当＋－>时，△为锐角三角形；当＋－＝时，△为直角三角形；当＋－<时，△为钝角三角形.( )()在三角形中，已知两边和一角就能求三角形的面积.( )解析()三角形中三边之比等于相应的三个内角的正弦值之比.()已知三角时，不可求三边.()当＋－>时，三角形不一定为锐角三角形.答案()×()√()×()×()√.(·全国Ⅰ卷)△的内角，，的对边分别为，，.已知＝，＝，＝，则＝( )解析由余弦定理，得＝＋－×××，解得＝，故选.答案.(·湖州预测)在△中，角，，所对的边分别为，，，若)＝，则＝( ).－.－解析由正弦定理知,() )＝)＝，即＝，由∈(，π)，所以＝，所以＝＝，故选.答案.在△中，＝°，＝，且△的面积为，则的长为( )解析因为＝××＝××＝，所以＝，所以＝＋－·°＝，所以＝.答案.(必修改编)在△中，＝，则这个三角形的形状为.解析由正弦定理，得＝，即＝，所以＝或＝π－，即＝或＋＝，所以这个三角形为等腰三角形或直角三角形.答案等腰三角形或直角三角形.(·绍兴调研)已知钝角△的面积为，＝，＝，则角＝，＝.解析∵钝角△的面积为，＝，＝，∴＝×××，解得＝，∴＝或，∵当＝时，由余弦定理可得＝)＝＝，此时，＋＝，可得＝，此△为直角三角形，与已知矛盾，舍去.∴＝，由余弦定理可得＝)＝＝.答案。

4-61．(2018·石家庄二检)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，则“sin A >sinB ”是“a >b ”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【解析】 设△ABC 外接圆的半径为R ，若sin A >sin B ，则2R sin A >2R sin B ，即a >b ；若a >b ，则a 2R >b2R ，即sin A >sin B ，所以在△ABC 中，“sin A >sin B ”是“a >b ”的充要条件，故选C.【答案】 C2．(2016·全国乙卷)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .已知a ＝5，c ＝2，cos A ＝23，则b 等于( )A. 2B. 3 C ．2D ．3【解析】 由余弦定理，得5＝b 2＋22－2×b ×2×23，解得b ＝3⎝ ⎛⎭⎪⎫b ＝－13舍去，故选D.【答案】 D3．(2018·西安模拟)设△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，若b cos C ＋c cos B ＝a sin A ，且sin 2B ＝sin 2C ，则△ABC 的形状为( )A ．等腰三角形B ．锐角三角形C ．直角三角形D ．等腰直角三角形【解析】 由b cos C ＋c cos B ＝a sin A ， 得sin B cos C ＋sin C cos B ＝sin 2A ， ∴sin(B ＋C )＝sin 2A ，即sin A ＝sin 2A ，在三角形中sin A ≠0， ∴sin A ＝1，∴A ＝90°， 由sin 2B ＝sin 2C ，知b ＝c ， 综上可知△ABC 为等腰直角三角形． 【答案】 D4．设△ABC 的内角A ，B ，C 所对边的长分别为a ，b ，c ，若b ＋c ＝2a ，3sin A ＝5sin B ，则角C 等于( )A.2π3 B.π3 C.3π4D.5π6【解析】 因为3sin A ＝5sin B ，所以由正弦定理可得3a ＝5b .因为b ＋c ＝2a ，所以c ＝2a －35a ＝75a .令a ＝5，b ＝3，c ＝7，则由余弦定理c 2＝a 2＋b 2－2ab cos C ，得49＝25＋9－2×3×5cos C ，解得cos C ＝－12，所以C ＝2π3.【答案】 A5．已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且c －b c －a ＝sin Asin C ＋sin B，则B 等于( )A.π6 B.π4 C.π3D.3π4【解析】 根据正弦定理a sin A ＝b sin B ＝csin C ＝2R ，得c －b c －a ＝sin A sin C ＋sin B ＝ac ＋b， 即a 2＋c 2－b 2＝ac ，得cos B ＝a 2＋c 2－b 22ac ＝12，故B ＝π3，故选C.【答案】 C6．△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知b ＝2，B ＝π6，C ＝π4，则△ABC的面积为( )A ．23＋2 B.3＋1 C ．23－2D.3－1【解析】 ∵b ＝2，B ＝π6，C ＝π4.由正弦定理b sin B ＝csin C，得c ＝b sin Csin B ＝2×2212＝22，A ＝π－⎝ ⎛⎭⎪⎫π6＋π4＝712π，∴sin A ＝sin ⎝ ⎛⎭⎪⎫π4＋π3＝sin π4cos π3＋cos π4sin π3＝6＋24. 则S △ABC ＝12bc ·sin A ＝12×2×22×6＋24＝3＋1.【答案】 B7．(2016·全国甲卷)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，若cos A ＝45，cosC ＝513，a ＝1，则b ＝________．【解析】 在△ABC 中，由cos A ＝45，cos C ＝513，可得sin A ＝35，sin C ＝1213，sin B＝sin(A ＋C )＝sin A cos C ＋cos A ·sin C ＝6365，由正弦定理得b ＝a sin B sin A ＝2113.【答案】 21138．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c .若(a 2＋c 2－b 2)tan B ＝3ac ，则角B 的值为________．【解析】 由余弦定理，得a 2＋c 2－b 22ac＝cos B ，结合已知等式得cos B ·tan B ＝32， ∴sin B ＝32，∴B ＝π3或2π3. 【答案】 π3或2π39．(2018·昆明检测)已知a ，b ，c 分别为△ABC 三个内角A ，B ，C 的对边，若cos B ＝45，a ＝10，△ABC 的面积为42，则b ＋asin A的值等于________． 【解析】 依题可得sin B ＝35，又S △ABC ＝12ac sin B ＝42，则c ＝14.故b ＝a 2＋c 2－2ac cos B ＝62， 所以b ＋a sin A ＝b ＋bsin B ＝16 2.【答案】 16 210．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且满足a sin B ＝3b cos A ．若a ＝4，则△ABC 周长的最大值为________．【解析】 由正弦定理a sin A ＝bsin B，可将a sin B ＝3b cos A 转化为sin A sin B ＝3sin B cos A. 又在△ABC 中，sin B >0，∴sin A ＝3cos A ， 即tan A ＝ 3. ∵0<A <π，∴A ＝π3.由余弦定理得a 2＝16＝b 2＋c 2－2bc cos A＝(b ＋c )2－3bc ≥(b ＋c )2－3⎝ ⎛⎭⎪⎫b ＋c 22，则(b ＋c )2≤64，即b ＋c ≤8(当且仅当b ＝c ＝4时等号成立)， ∴△ABC 周长＝a ＋b ＋c ＝4＋b ＋c ≤12，即最大值为12. 【答案】 1211. (2017·全国Ⅱ卷)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知sin(A ＋C )＝8sin 2B2.(1)求cos B ；(2)若a ＋c ＝6，△ABC 的面积为2，求b .【解析】 (1)由题设及A ＋B ＋C ＝π得sin B ＝8sin 2B2，故sin B ＝4(1－cos B )．上式两边平方，整理得17cos 2B －32cos B ＋15＝0， 解得cos B ＝1(舍去)，或cos B ＝1517.故cos B ＝1517.(2)由cos B ＝1517得sin B ＝817，故S △ABC ＝12ac sin B ＝417ac .又S △ABC ＝2，则ac ＝172.由余弦定理及a ＋c ＝6得b 2＝a 2＋c 2－2ac cos B ＝(a ＋c )2－2ac (1＋cos B )＝36－2×172×⎝ ⎛⎭⎪⎫1＋1517＝4.所以b ＝2.12．(2018·云南二检)已知a ，b ，c 分别是△ABC 的内角A ，B ，C 对的边，b ＝ 3. (1)若C ＝5π6，△ABC 的面积为32，求c ；(2)若B ＝π3，求2a －c 的取值范围．【解析】 (1)∵C ＝5π6，△ABC 的面积为32，b ＝3，∴12ab sin C ＝12×a ×3×12＝32. ∴a ＝2.由余弦定理得c 2＝a 2＋b 2－2ab cos C ＝4＋3－2×2×3×⎝ ⎛⎭⎪⎫－32＝13. ∴c ＝13.(2)由正弦定理得a sin A ＝b sin B ＝csin C ，∴a ＝b sin A sin B ＝2sin A ，c ＝b sin Csin B＝2sin C . ∴2a －c ＝4sin A －2sin C ＝4sin ⎝ ⎛⎭⎪⎫2π3－C －2sin C＝4⎝ ⎛⎭⎪⎫sin 2π3cos C －cos 2π3sin C －2sin C＝23cos C . ∵B ＝π3，∴0<C <2π3，∴－12<cos C <1，∴－3<23cos C <23，∴2a －c 的取值范围为(－3，23).。

一、选择题1．(2016·隆化期中)在△ABC 中，如果sin A ∶sin B ∶sin C ＝2∶3∶4，那么cos C 等于( ) A.23 B ．－23C ．－13D ．－142．北京2008年第29届奥运会开幕式上举行升旗仪式，在坡度15°的看台上，同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°，第一排和最后一排的距离为106米(如图所示)，旗杆底部与第一排在一个水平面上，已知国歌长度为50秒，升旗手匀速升旗的速度为( )A.35(米/秒) B.35(米/秒) C.65(米/秒) D.15(米/秒) 3．(2016·安庆检测)在△ABC 中，内角A 、B 、C 的对边分别是a 、b 、c .若a 2－c 2＝3bc ，sin B ＝23sin C ，则A 等于( ) A.56π B.23π C.π3D.π64．(2017·武汉调研)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且b 2＝a 2＋bc ，A ＝π6，则角C 等于( ) A.π6 B.π4 C.3π4D.π4或3π45．(2016·衡水中学第二学期调研)设锐角△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，且a ＝1，B ＝2A ，则b 的取值范围为( ) A ．(2，3) B ．(1，3) C ．(2，2)D ．(0,2)6．(2016·东营期中)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，S 表示△ABC 的面积，若a cos B ＋b cos A ＝c sin C ，S ＝14(b 2＋c 2－a 2)，则B 等于( )A ．90°B ．60°C ．45°D ．30°7．(2016·山西大学附中期中)已知三个向量m ＝⎝ ⎛⎭⎪⎫a ，cos A 2，n ＝⎝ ⎛⎭⎪⎫b ，cos B 2，p ＝⎝ ⎛⎭⎪⎫c ，cos C 2共线，其中a 、b 、c 、A 、B 、C 分别是△ABC 的三条边及相对三个角，则△ABC 的形状是( ) A ．等腰三角形 B ．等边三角形 C ．直角三角形D ．等腰直角三角形8．已知点O 是△ABC 的外接圆圆心，且AB ＝3，AC ＝4.若存在非零实数x ，y ，使得AO →＝xAB →＋yAC →，且x ＋2y ＝1，则cos ∠BAC 的值为( ) A.23 B.33C.23D.13二、填空题9．△ABC 中，A 、B 、C 是其内角，若sin 2A ＋sin(A －C )－sin B ＝0，则△ABC 的形状是__________________．10．(2016·惠州二调)在△ABC 中，设角A ，B ，C 的对边分别是a ，b ，c ，且∠C ＝60°，c ＝3，则a ＋23cos Asin B＝________.11．(2016·佛山期中)如图，一艘船以每小时15 km 的速度向东航行，船在A 处看到一灯塔M在北偏东60°方向，行驶4 h后，船到达B处，看到这个灯塔在北偏东15°方向，这时船与灯塔的距离为________ km.12．(2016·吉安期中)在△ABC中，D为BC边上一点，若△ABD是等边三角形，且AC＝43，则△ADC的面积的最大值为________.答案精析1．D [由正弦定理可得sin A ∶sin B ∶sin C ＝a ∶b ∶c ＝2∶3∶4，可设a ＝2k ，b ＝3k ，c＝4k (k >0)，由余弦定理可得cos C ＝a 2＋b 2－c 22ab ＝4k 2＋9k 2－16k 22·2k ·3k ＝－14.]2．A [由条件得△ABD 中，∠DAB ＝45°，∠ABD ＝105°，∠ADB ＝30°，AB ＝106，由正弦定理得BD ＝sin ∠DABsin ∠ADB ·AB ＝203，则在Rt △BCD 中，CD ＝203×sin 60°＝30，所以速度v ＝3050＝35(米/秒)，故选A.]3．D [已知sin B ＝23sin C ，利用正弦定理化简得b ＝23c ，代入a 2－c 2＝3bc ，得a 2－c 2＝6c 2，即a ＝7c ，∴cos A ＝b 2＋c 2－a 22bc ＝12c 2＋c 2－7c 243c2＝32. ∵A 为三角形内角，∴A ＝π6，故选D.]4．B [在△ABC 中，由余弦定理，得cos A ＝b 2＋c 2－a 22bc ，即32＝b 2＋c 2－a 22bc，所以b 2＋c 2－a 2＝3bc ，又b 2＝a 2＋bc ，所以c 2＋bc ＝3bc ，所以c ＝(3－1)b <b ，a ＝2－3b ， 所以cos C ＝b 2＋a 2－c 22ab ＝22，所以C ＝π4.]5．A [∵B ＝2A ，∴sin B ＝sin 2A ， ∴sin B ＝2sin A cos A ，∴b ＝2a cos A ， 又∵a ＝1，∴b ＝2cos A . ∵△ABC 为锐角三角形， ∴0<A <π2，0<B <π2，0<C <π2，即0<A <π2，0<2A <π2，0<π－A －2A <π2，∴π6<A <π4，∴22<cos A <32， ∴2<2cos A <3，∴b ∈(2，3)．]6．C [由正弦定理可知a cos B ＋b cos A ＝2R sin A cos B ＋2R sin B cos A ＝2R sin(A ＋B )＝2R sinC ＝2R sin C ·sin C ，∴sin C ＝1，C ＝90°.∴S ＝12ab ＝14(b 2＋c 2－a 2)，解得a ＝b ，因此B ＝45°.故选C.]7．B [∵m ＝⎝ ⎛⎭⎪⎫a ，cos A 2与n ＝⎝ ⎛⎭⎪⎫b ，cos B 2共线，∴a cos B 2＝b cos A2，由正弦定理，得sin A cos B 2＝sin B cos A2， ∵sin A ＝2sin A 2cos A 2，sin B ＝2sin B 2cos B2，∴2sin A 2cos A 2cos B 2＝2sin B 2cos B 2cos A2，化简，得sin A 2＝sin B2.又0<A 2<π2，0<B 2<π2，∴A 2＝B2，可得A ＝B . 同理，由n ＝⎝ ⎛⎭⎪⎫b ，cos B 2与p ＝⎝ ⎛⎭⎪⎫c ，cos C 2共线得到B ＝C ，∴A ＝B ＝C ，可得△ABC 是等边三角形．] 8．A [设线段AC 的中点为点D ，则直线OD ⊥AC . 因为AO →＝xAB →＋yAC →，所以AO →＝xAB →＋2yAD →. 又x ＋2y ＝1，所以点O 、B 、D 三点共线， 即点B 在线段AC 的中垂线上，则AB ＝BC ＝3.在△ABC 中，由余弦定理，得cos ∠BAC ＝32＋42－322×3×4＝23.故选A.]9．等腰或直角三角形解析 因为sin 2A ＋sin(A －C )－sin B ＝sin 2A ＋sin(A －C )－sin(A ＋C ) ＝2sin A cos A －2sin C cos A ＝2cos A (sin A －sin C )＝0， 所以cos A ＝0或sin A ＝sin C ， 所以A ＝π2或A ＝C .故△ABC 为等腰或直角三角形． 10．4解析 由正弦定理知a sin A ＝csin C＝2，所以a ＝2sin A ，代入得原式＝2sin A ＋23cos A sin B ＝4·sin(A ＋60°)sin B ＝4.11．30 2解析 依题意有AB ＝15×4＝60，∠MAB ＝30°，∠AMB ＝45°， 在△AMB 中，由正弦定理得60sin 45°＝BMsin 30°，解得BM ＝30 2.12．4 3解析 在△ACD 中，cos ∠ADC ＝AD 2＋DC 2－AC 22AD ·DC ＝AD 2＋DC 2－482AD ·DC ＝－12，整理得AD 2＋DC 2＝48－AD ·DC ≥2AD ·DC ， ∴AD ·DC ≤16，当且仅当AD ＝CD 时等号成立， ∴△ADC 的面积S ＝12AD ·DC ·sin ∠ADC ＝34AD ·DC ≤4 3.。

第六节正弦定理和余弦定理本节主要包括3个知识点：1.利用正、余弦定理解三角形；2.利用正、余弦定理判断三角形的形状；3.正、余弦定理的综合应用.突破点(一)利用正、余弦定理解三角形基础联通抓主干知识的“源”与“流”(1)已知两角和任一边，求其他两边和一角．(2)已知两边和其中一边的对角，求另一边的对角，从而进一步求出其他的边和角．由于三角形的形状不能唯一确定，会出现两解、一解和无解三种情况．在△ABC中，已知a，b和A，解的个数见下表a >b 一解 一解 一解 a ＝b无解无解一解 a <b 无解 无解 a >b sin A两解 a ＝b sin A 一解 a <b sin A无解[例1] (1)在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c .若a sin B cos C ＋c sin B cos A ＝12b ，且a >b ，则B ＝( )A.π6B.π3C.2π3D.5π6(2)设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .若a ＝3，sin B ＝12，C ＝π6，则b＝________.[解析] (1)利用正弦定理的变形，得a ＝2R sin A ，b ＝2R sin B ，c ＝2R sin C ，代入a sin B cos C ＋c sin B cos A ＝12b 中，得2R sin A ·sin B cos C ＋2R sin C sin B cos A ＝12×2R sin B ，所以sinA cos C ＋sin C cos A ＝12，即sin(A ＋C )＝12，所以sinB ＝12.已知a >b ，所以B 不是最大角，所以B ＝π6.(2)在△ABC 中，∵sin B ＝12，0<B <π，∴B ＝π6或B ＝5π6.又∵B ＋C <π，C ＝π6，∴B ＝π6，∴A ＝π－π6－π6＝2π3.∵a sin A ＝b sin B ，∴b ＝a sin B sin A ＝1. [答案] (1)A (2)1 [易错提醒](1)应用正弦定理求角时容易出现增解或漏解的错误，要根据条件和三角形的限制条件合理取舍．(2)求角时易忽略角的范围而导致错误，需要根据大边对大角，大角对大边的规则，画图帮助判断．利用余弦定理解三角形(1)已知两边及夹角，先求第三边，再求其余两个角． (2)已知三边，求三个内角．[例2] (1)在△ABC 中，已知a －b ＝4，a ＋c ＝2b ，且最大角为120°，则这个三角形的最大边等于( )A ．4B ．14C ．4或14D ．24(2)设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且a cos C ＋32c ＝b ，则A ＝________. [解析] (1)因为a －b ＝4，所以b ＝a －4且a >b .又a ＋c ＝2b ，所以c ＝a －8，所以a 大于c ，则A ＝120°.由余弦定理得a 2＝b 2＋c 2－2bc cos A ＝(a －4)2＋(a －8)2－2(a －4)·(a －8)·⎝⎛⎭⎫－12，所以a 2－18a ＋56＝0.所以a ＝14或a ＝4(舍去)．故选B.(2)由余弦定理得cos C ＝a 2＋b 2－c 22ab ，将其代入a cos C ＋32c ＝b 中得，a ×a 2＋b 2－c 22ab ＋32c ＝b ，化简整理得b 2＋c 2－a 2＝3bc ，于是cos A ＝b 2＋c 2－a 22bc ＝32，所以A ＝π6.[答案] (1)B (2)π6利用正、余弦定理解三角形[例3] 设△3，c ＝1，A ＝2B . (1)求a 的值； (2)求sin ⎝⎛⎭⎫A ＋π4的值． [解] (1)因为A ＝2B ，所以sin A ＝sin 2B ＝2sin B cos B . 由正、余弦定理，得a ＝2b ·a 2＋c 2－b 22ac .因为b ＝3，c ＝1，所以a 2＝12，a ＝2 3.(2)由余弦定理，得cos A ＝b 2＋c 2－a 22bc ＝9＋1－126＝－13.因为0<A <π，所以sin A ＝1－cos 2A ＝1－19＝223. 故sin ⎝⎛⎭⎫A ＋π4＝sin A cos π4＋cos A sin π4＝4－26.[方法技巧]正、余弦定理的运用技巧解三角形时，一般是根据正弦定理求边或列等式，若式子中含有角的正弦或边的一次式时，则考虑用正弦定理；余弦定理揭示的是三角形的三条边与其中一个角之间的关系，若式子中含有角的余弦或边的二次式，则考虑用余弦定理；若以上特征都不明显，则要考虑两个定理都有可能用到．能力练通 抓应用体验的“得”与“失” 1.[考点一]在锐角△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若b ＝2a sin B ，则A ＝( )A ．30°B ．45°C ．60°D ．75°解析：选A 因为在锐角△ABC 中，b ＝2a sin B ，由正弦定理得，sin B ＝2sin A sin B ，所以sin A ＝12，又0°<A <90°，所以A ＝30°.2.[考点二](2016·兰州一模)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若a ＝7，b ＝3，c ＝2，则A ＝( )A.π6B.π4C.π3D.π2解析：选C 由余弦定理，得cos A ＝b 2＋c 2－a 22bc ＝32＋22－(7)22×3×2＝12，又A ∈(0，π)，∴A ＝π3，故选C.3.[考点二]设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .若a ＝2，c ＝2 3，cos A ＝32且b ＜c ，则b ＝( ) A ．3 B ．2 2 C ．2 D. 3解析：选C 由余弦定理得，a 2＝b 2＋c 2－2bc cos A ，即4＝b 2＋12－6b ，解得b ＝2或4.又b ＜c ，∴b ＝2.4.[考点一](2017·合肥模拟)在△ABC 中，AB ＝2，AC ＝3，B ＝60°，则cos C ＝________. 解析：由正弦定理，得AB sin C ＝AC sin B ，即2sin C ＝3sin 60°，解得sin C ＝33. ∵AB <AC ，∴C <B ，∴cos C ＝1－sin 2C ＝63. 答案：635.[考点三]设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且a ＝2，cos C ＝－14，3sinA ＝2sinB ，则c ＝________.解析：∵3sin A ＝2sin B ，∴由正弦定理可得3a ＝2b .又a ＝2，∴b ＝3.由余弦定理可知c 2＝a 2＋b 2－2ab cos C ，∴c 2＝22＋32－2×2×3×⎝⎛⎭⎫－14＝16，∴c ＝4. 答案：46.[考点三]在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，已知sin 2B ＋sin 2C ＝sin 2A ＋sin B sin C .(1)求角A 的大小；(2)若cos B ＝13，a ＝3，求c 的值．解：(1)由正弦定理可得b 2＋c 2＝a 2＋bc ， 由余弦定理得cos A ＝b 2＋c 2－a 22bc ＝12，因为A ∈(0，π)，所以A ＝π3.(2)由(1)可知sin A ＝32， 因为cos B ＝13，B 为△ABC 的内角，所以sin B ＝223，故sin C ＝sin(A ＋B )＝sin A cos B ＋cos A sin B ＝32×13＋12×223＝3＋226. 由正弦定理a sin A ＝c sin C 得c ＝a sin A sin C ＝332×3＋226＝1＋263. 突破点(二) 利用正、余弦定理判断三角形的形状1．应用余弦定理判断三角形形状的方法 在△ABC 中，c 是最大的边，若c 2<a 2＋b 2，则△ABC 是锐角三角形； 若c 2＝a 2＋b 2，则△ABC 是直角三角形； 若c 2>a 2＋b 2，则△ABC 是钝角三角形． 2．判断三角形形状的常用技巧 若已知条件中既有边又有角，则(1)化边：通过因式分解、配方等得出边的相应关系，从而判断三角形的形状． (2)化角：通过三角恒等变换，得出内角的关系，从而判断三角形的形状．此时要注意应用A ＋B ＋C ＝π这个结论.[典例] (1)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若cb <cos A ，则△ABC为( )A ．钝角三角形B ．直角三角形C ．锐角三角形D ．等边三角形(2)(2017·锦州模拟)在△ABC 中，cos 2B 2＝a ＋c2c (a ，b ，c 分别为角A ，B ，C 的对边)，则△ABC 的形状为( )A ．等边三角形B ．直角三角形C ．等腰三角形或直角三角形D ．等腰直角三角形[解析] (1)已知c b <cos A ，由正弦定理，得sin Csin B <cos A ，即sin C <sin B cos A ，所以sin(A＋B )<sin B cos A ，即sin B ·cos A ＋cos B sin A －sin B cos A <0，所以cos B sin A <0.又sin A >0，于是有cos B <0，则B 为钝角，所以△ABC 是钝角三角形．(2)∵cos 2B2＝a ＋c 2c ，∴1＋cos B 2＝a ＋c2c，即1＋cos B ＝a ＋cc .由余弦定理得1＋a 2＋c 2－b 22ac＝a ＋cc .整理得c 2＝a 2＋b 2，即△ABC 为直角三角形． [答案] (1)A (2)B [易错提醒]在判断三角形的形状时一定要注意解是否唯一，并注重挖掘隐含条件．另外，在变形过程中要注意角A ，B ，C 的范围对三角函数值的影响，在等式变形中，一般两边不要约去公因式，应移项提取公因式，以免漏解．能力练通 抓应用体验的“得”与“失”1．设△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，若2sin A cos B ＝sin C ，那么△ABC 一定是( )A ．直角三角形B ．等腰三角形C ．等腰直角三角形D ．等边三角形解析：选B 由正弦定理得2a cos B ＝c ，再由余弦定理得2a ·a 2＋c 2－b 22ac＝c ，整理得a 2＝b 2，即a ＝b ，所以△ABC 是等腰三角形．2．(2017·浙江金丽衢十二校联考)已知△ABC 的三个内角A ，B ，C 的对边分别为a ，b ，c ，若cos A cos B ＝b a＝2，则该三角形的形状是( )A ．直角三角形B ．等腰三角形C ．等边三角形D ．钝角三角形解析：选A 因为cos A cos B ＝b a ，由正弦定理得cos A cos B ＝sin B sin A ，所以sin 2A ＝sin 2B .由ba ＝2，可知a ≠b ，所以A ≠B .又A ，B ∈(0，π)，所以2A ＝180°－2B ，即A ＋B ＝90°，所以C ＝90°，于是△ABC 是直角三角形．故选A.3．在△ABC 中，若(a 2＋b 2)sin(A －B )＝(a 2－b 2)sin(A ＋B )，则△ABC 的形状是( ) A ．等腰三角形 B ．直角三角形C ．等腰直角三角形D ．等腰三角形或直角三角形解析：选D 因为(a 2＋b 2)sin(A －B )＝(a 2－b 2)sin(A ＋B )，所以b 2[sin(A ＋B )＋sin(A －B )]＝a 2[sin(A ＋B )－sin(A －B )]，化简整理得a 2cos A sin B ＝b 2sin A cosB ．由正弦定理、余弦定理得，a 2b b 2＋c 2－a 22bc ＝b 2a a 2＋c 2－b22ac，所以a 2(b 2＋c 2－a 2)＝b 2(a 2＋c 2－b 2)，即(a 2－b 2)(a 2＋b 2－c 2)＝0，所以a 2－b 2＝0或a 2＋b 2－c 2＝0，即a ＝b 或a 2＋b 2＝c 2.所以△ABC 为等腰三角形或直角三角形．4．在△ABC 中，已知a 2＋b 2－c 2＝ab ，且2cos A sin B ＝sin C ，试判断△ABC 的形状． 解：由正弦定理得sin C sin B ＝cb，由2cos A sin B ＝sin C ，有cos A ＝sin C 2sin B ＝c2b .又由余弦定理得cos A ＝b 2＋c 2－a 22bc，∴c 2b ＝b 2＋c 2－a 22bc， 即c 2＝b 2＋c 2－a 2， 所以a 2＝b 2，所以a ＝b . 又∵a 2＋b 2－c 2＝ab ， ∴2b 2－c 2＝b 2，所以b 2＝c 2， ∴b ＝c ，∴a ＝b ＝c . ∴△ABC 为等边三角形．突破点(三) 正、余弦定理的综合应用三角形面积问题三角形的面积是与解三角形息息相关的内容，经常出现在高考题中，难度不大．解题的前提条件是熟练掌握三角形面积公式，具体的题型及解题策略为：(1)利用正弦定理、余弦定理解三角形，求出三角形的有关元素之后，直接求三角形的面积，或求出两边之积及夹角正弦，再求解．(2)把面积作为已知条件之一，与正弦定理、余弦定理结合求出三角形的其他各量．面积公式中涉及面积、两边及两边夹角正弦四个量，结合已知条件列方程求解．[例1] 在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且(2b －c )cos A ＝a cos C . (1)求角A 的大小；(2)若a ＝3，b ＝2c ，求△ABC 的面积．[解] (1)根据正弦定理，由(2b －c )cos A ＝a cos C ， 得2sin B cos A ＝sin A cos C ＋sin C cos A ， 即2sin B cos A ＝sin(A ＋C )， 所以2sin B cos A ＝sin B ， 因为0<B <π，所以sin B ≠0，所以cos A ＝12，因为0<A <π，所以A ＝π3.(2)因为a ＝3，b ＝2c ，由(1)得A ＝π3，所以cos A ＝b 2＋c 2－a 22bc ＝4c 2＋c 2－94c 2＝12，解得c ＝3，所以b ＝2 3.所以S △ABC ＝12bc sin A ＝12×23×3×32＝332.[方法技巧]三角形面积公式的应用原则(1)对于面积公式S ＝12ab sin C ＝12ac sin B ＝12bc sin A ，一般是已知哪一个角就使用哪一个公式．(2)与面积有关的问题，一般要用到正弦定理或余弦定理进行边和角的转化．解三角形问题中，求解某个量(式子)的取值范围是命题的热点，其主要解决思路是： 要建立所求量(式子)与已知角或边的关系，然后把角或边作为自变量，所求量(式子)的值作为函数值，转化为函数关系，将原问题转化为求函数的值域问题．这里要利用条件中的范围限制，以及三角形自身范围限制，要尽量把角或边的范围(也就是函数的定义域)找完善，避免结果的范围过大．[例2] 设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，a ＝b tan A ，且B 为钝角． (1)证明：B －A ＝π2；(2)求sin A ＋sin C 的取值范围．[解] (1)证明：由a ＝b tan A 及正弦定理，得sin A cos A ＝a b ＝sin Asin B ，所以sin B ＝cos A ，即sin B ＝sin ⎝⎛⎭⎫π2＋A . 因为B 为钝角，所以A 为锐角， 所以π2＋A ∈⎝⎛⎭⎫π2，π， 则B ＝π2＋A ，即B －A ＝π2.(2)由(1)知，C ＝π－(A ＋B )＝π－⎝⎛⎭⎫2A ＋π2＝π2－2A >0， 所以A ∈⎝⎛⎭⎫0，π4. 于是sin A ＋sin C ＝sin A ＋sin ⎝⎛⎭⎫π2－2A ＝sin A ＋cos 2A ＝－2sin 2A ＋sin A ＋1 ＝－2⎝⎛⎭⎫sin A －142＋98. 因为0<A <π4，所以0<sin A <22， 因此22<－2⎝⎛⎭⎫sin A －142＋98≤98.由此可知sin A ＋sin C 的取值范围是⎝⎛⎦⎤22，98. [易错提醒]涉及求范围的问题，一定要搞清已知变量的范围，利用已知的范围进行求解，已知边的范围求角的范围时可以利用余弦定理进行转化．正、余弦定理在平面几何中的应用在平面几何图形中考查正弦定理、余弦定理是近几年高考的热点，解决这类问题既要抓住平面图形的几何性质，也要灵活选择正弦定理、余弦定理、三角恒等变换公式．此类题目求解时，一般有如下思路：(1)把所提供的平面图形拆分成若干个三角形，然后在各个三角形内利用正弦、余弦定理求解；(2)寻找各个三角形之间的联系，交叉使用公共条件，求出结果．做题过程中，要用到平面几何中的一些知识点，如相似三角形的边角关系、平行四边形的一些性质，要把这些性质与正弦、余弦定理有机结合，才能顺利解决问题．[例3] (2017·广东茂名模拟)如图，已知在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c .若B ＝π3，b ＝7，c ＝2，D 为BC 的中点．(1)求cos ∠BAC 的值； (2)求AD 的值．[解] (1)法一：由正弦定理得sin C ＝c b sin B ＝27×32＝37.又∵在△ABC 中，b >c ，∴C <B ，∴0<C <π3，∴cos C ＝1－sin 2C ＝1－37＝27， ∴cos ∠BAC ＝cos(π－B －C )＝－cos(B ＋C ) ＝－(cos B cos C －sin B sin C ) ＝sin B sin C －cos B cos C ＝32×37－12×27＝714.法二：在△ABC 中，由余弦定理得b 2＝c 2＋a 2－2c ·a cos B ，∴7＝4＋a 2－2×2×a ×12，即(a －3)(a ＋1)＝0，解得a ＝3(a ＝－1舍去)， ∴cos ∠BAC ＝c 2＋b 2－a 22cb ＝4＋7－92×2×7＝714.(2)法一：在△ABC 中，由余弦定理得a 2＝c 2＋b 2－2c ·b cos ∠BAC ＝4＋7－2×2×7×714＝9.∴a ＝3，∴BD ＝32.在△ABD 中，由余弦定理得AD 2＝AB 2＋BD 2－2AB ·BD ·cos B ＝4＋94－2×2×32×12＝134.∴AD ＝132. 法二：如图，取AC 的中点E ，连接DE ，则DE ＝12AB ＝1，AE ＝12AC ＝72，cos ∠AED ＝－cos ∠BAC .在△ADE 中，由余弦定理得AD 2＝AE 2＋DE 2－2AE ·DE ·cos ∠AED ＝74＋1－2×72×1×⎝⎛⎭⎫－714＝134.∴AD ＝132.1.[考点一]在△ABC 中，内角A ，B ，C 所对的边分别是a ，b ，c .若c 2＝(a －b )2＋6，C ＝π3，则△ABC 的面积是( ) A ．3 B.932 C.332D ．3 3解析：选C 由余弦定理得，c 2＝a 2＋b 2－2ab cos C ＝a 2＋b 2－ab ＝(a －b )2＋6，∴ab ＝6， ∴S △ABC ＝12ab sin C ＝12×6×32＝332.2.[考点三]如图，在△ABC 中，C ＝π3，BC ＝4，点D 在边AC 上，AD ＝DB ，DE ⊥AB ，E 为垂足，若DE ＝22，则cos A ＝( )A.223B.24C.64 D.63解析：选C 因为DE ⊥AB ，DE ＝22，所以AD ＝22sin A ，所以DB ＝AD ＝22sin A .因为AD ＝DB ，所以A ＝∠ABD ，所以∠BDC ＝A ＋∠ABD ＝2A .在△BCD 中，由正弦定理DBsin C＝BC sin ∠BDC，得22sin A 32＝4sin 2A ，化简整理得cos A ＝64.3.[考点二](2017·海淀模拟)△ABC 的三个内角A ，B ，C 所对的边分别为a ，b ，c ，a sin A sin B ＋b cos 2A ＝2a ，则角A 的取值范围是________．解析：由已知及正弦定理得sin 2A sin B ＋sin B cos 2A ＝2sin A ，即sin B (sin 2A ＋cos 2A )＝2sin A ，∴sin B ＝2sin A ，∴b ＝2a ，由余弦定理得cos A ＝b 2＋c 2－a 22bc ＝4a 2＋c 2－a 24ac ＝3a 2＋c 24ac ≥23ac 4ac ＝32，当且仅当c ＝3a 时取等号，∵A 为三角形的内角，且y ＝cos x 在(0，π)上是减函数，∴0<A ≤π6，则角A 的取值范围是⎝⎛⎦⎤0，π6. 答案：⎝⎛⎦⎤0，π6 4.[考点二](2017·广东揭阳模拟)已知△ABC 中，角A ，32B ，C 成等差数列，且△ABC的面积为1＋2，则AC 边的长的最小值是________．解析：∵A ，32B ，C 成等差数列，∴A ＋C ＝3B ，又A ＋B ＋C ＝π，∴B ＝π4.设角A ，B ，C所对的边分别为a ，b ，c ，由S △ABC ＝12ac sin B ＝1＋2得ac ＝2(2＋2)，由余弦定理及a 2＋c 2≥2ac ，得b 2≥(2－2)ac ，即b 2≥(2－2)×2(2＋2)，∴b ≥2(当且仅当a ＝c 时等号成立)，∴AC 边的长的最小值为2.答案：25.[考点一]已知△ABC 是斜三角形，内角A ，B ，C 所对的边的长分别为a ，b ，c .若c sin A ＝3a cos C .(1)求角C ；(2)若c ＝21，且sin C ＋sin(B －A )＝5sin 2A ，求△ABC 的面积． 解：(1)根据a sin A ＝c sin C，可得c sin A ＝a sin C ，又∵c sin A ＝3a cos C ，∴a sin C ＝3a cos C ， ∴sin C ＝3cos C ，∴tan C ＝sin Ccos C＝3， ∵C ∈(0，π)，∴C ＝π3.(2)∵sin C ＋sin(B －A )＝5sin 2A ，sin C ＝sin(A ＋B )， ∴sin(A ＋B )＋sin(B －A )＝5sin 2A ， ∴2sin B cos A ＝5×2sin A cos A .∵△ABC 为斜三角形，∴cos A ≠0，∴sin B ＝5sin A . 由正弦定理可知b ＝5a ，① 由余弦定理c 2＝a 2＋b 2－2ab cos C ， ∴21＝a 2＋b 2－2ab ×12＝a 2＋b 2－ab ，②由①②解得a ＝1，b ＝5，∴S △ABC ＝12ab sin C ＝12×1×5×32＝534.[全国卷5年真题集中演练——明规律] 1．(2016·全国丙卷)在△ABC 中，B ＝π4，BC 边上的高等于13BC ，则cos A ＝( )A.31010B.1010 C ．－1010D ．－31010解析：选C 设△ABC 中角A ，B ，C 所对的边分别为a ，b ，c ，则由题意得S △ABC ＝12a ·13a ＝12ac sin B ，又B ＝π4，所以c ＝23a .由余弦定理得b 2＝a 2＋c 2－2ac cos B ＝a 2＋29a 2－2×a ×23a ×22＝59a 2，所以b ＝53a .所以cos A ＝b 2＋c 2－a 22bc ＝59a 2＋29a 2－a 22×53a ×23a＝－1010.2．(2014·新课标全国卷Ⅱ)钝角三角形ABC 的面积是12，AB ＝1，BC ＝2，则AC ＝( )A ．5 B. 5 C ．2D ．1解析：选B 由题意可得12AB ·BC ·sin B ＝12，又AB ＝1，BC ＝2，所以sin B ＝22，所以B ＝45°或B ＝135°.当B ＝45°时，由余弦定理可得 AC ＝AB 2＋BC 2－2AB ·BC ·cos B ＝1，此时AC ＝AB ＝1，BC ＝2，易得A ＝90°， 与“钝角三角形”条件矛盾，舍去． 所以B ＝135°.由余弦定理可得 AC ＝AB 2＋BC 2－2AB ·BC ·cos B ＝ 5.3．(2016·全国甲卷)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，若cos A ＝45，cos C＝513，a ＝1，则b ＝________. 解析：在△ABC 中，∵cos A ＝45，cos C ＝513，∴sin A ＝35，sin C ＝1213，∴sin B ＝sin(A ＋C )＝sin A cos C ＋cos A sin C ＝35×513＋45×1213＝6365.又∵a sin A ＝b sin B ，∴b ＝a sin Bsin A ＝1×636535＝2113.答案：21134．(2015·新课标全国卷Ⅰ)在平面四边形ABCD 中，∠A ＝∠B ＝∠C ＝75°，BC ＝2，则AB 的取值范围是________．解析：如图所示，延长BA ，CD ，两延长线相交于点E ，过点C 作CF ∥AD 交AB 于点F ，则BF <AB <BE .在等腰三角形CFB 中，∠FCB ＝30°，CF ＝BC ＝2，∴BF ＝22＋22－2×2×2cos 30°＝6－ 2.在等腰三角形ECB 中，∠CEB ＝30°，∠ECB ＝75°， BE ＝CE ，BC ＝2，BE sin 75°＝2sin 30°，∴BE ＝212×6＋24＝6＋ 2.∴6－2<AB <6＋ 2. 答案：(6－2，6＋2)5．(2014·新课标全国卷Ⅰ)已知a ，b ，c 分别为△ABC 的三个内角A ，B ，C 的对边，a ＝2，且(2＋b )(sin A －sin B )＝(c －b )sin C ，则△ABC 面积的最大值为________．解析：由正弦定理得(2＋b )(a －b )＝(c －b )c ， 即(a ＋b )·(a －b )＝(c －b )c ，即b 2＋c 2－a 2＝bc ， 所以cos A ＝b 2＋c 2－a 22bc ＝12，又A ∈(0，π)，所以A ＝π3，又b 2＋c 2－a 2＝bc ≥2bc －4，即bc ≤4，故S △ABC ＝12bc sin A ≤12×4×32＝3，当且仅当b ＝c ＝2时，等号成立，则△ABC 面积的最大值为 3.答案： 36．(2016·全国乙卷)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知2cos C (a cos B ＋b cos A )＝c .(1)求C ；(2)若c ＝7，△ABC 的面积为332，求△ABC 的周长． 解：(1)由已知及正弦定理得2cos C (sin A cos B ＋sin B cos A )＝sin C ， 即2cos C sin(A ＋B )＝sin C ， 故2sin C cos C ＝sin C . 可得cos C ＝12，所以C ＝π3.(2)由已知得12ab sin C ＝332.又C ＝π3，所以ab ＝6.由已知及余弦定理得a 2＋b 2－2ab cos C ＝c 2， 故a 2＋b 2＝13，从而(a ＋b )2＝25，即a ＋b ＝5.所以△ABC 的周长为a ＋b ＋c ＝5＋7.7．(2015·新课标全国卷Ⅱ)△ABC 中，D 是BC 上的点，AD 平分∠BAC ，△ABD 面积是△ADC 面积的2倍．(1)求sin Bsin C； (2)若AD ＝1，DC ＝22，求BD 和AC 的长． 解：(1)S △ABD ＝12AB ·AD sin ∠BAD ，S △ADC ＝12AC ·AD sin ∠CAD .因为S △ABD ＝2S △ADC ，∠BAD ＝∠CAD ，所以AB ＝2AC . 由正弦定理，得sin B sin C ＝AC AB ＝12.(2)因为S △ABD ∶S △ADC ＝BD ∶DC ，所以BD ＝2DC ＝ 2. 在△ABD 和△ADC 中，由余弦定理，知 AB 2＝AD 2＋BD 2－2AD ·BD cos ∠ADB ， AC 2＝AD 2＋DC 2－2AD ·DC cos ∠ADC . 故AB 2＋2AC 2＝3AD 2＋BD 2＋2DC 2＝6. 由(1)，知AB ＝2AC ， 所以AC ＝1.8．(2013·新课标全国卷Ⅰ)如图，在△ABC 中，∠ABC ＝90°，AB＝3，BC ＝1，P 为△ABC 内一点，∠BPC ＝90°.(1)若PB ＝12，求PA ；(2)若∠APB ＝150°，求tan ∠PBA .解：(1)由已知得，∠PBC ＝60°，所以∠PBA ＝30°.在△PBA 中，由余弦定理得PA 2＝AB 2＋PB 2－2AB ·PB cos ∠PBA ＝3＋14－2×3×12cos 30°＝74.故PA ＝72.(2)设∠PBA ＝α，由已知得PB BC ＝cos ⎝⎛⎭⎫π2－α，即PB ＝sin α.在△PBA 中，由正弦定理得3sin 150°＝sin αsin (30°－α)，化简得3cos α＝4sin α. 所以tan α＝34，即tan ∠PBA ＝34. [课时达标检测] 重点保分课时——一练小题夯双基，二练题点过高考[练基础小题——强化运算能力]1．在△ABC 中，若sin A a ＝cos Bb ，则B 的值为( ) A ．30° B ．45° C ．60°D ．90°解析：选B 由正弦定理知，sin A sin A ＝cos Bsin B，∴sin B ＝cos B ，∴B ＝45°.2．在△ABC 中，已知AB ＝3，A ＝120°，且△ABC 的面积为1534，则BC ＝( )A ．3B ．5C ．7D ．15解析：选C 由S △ABC ＝1534得12×3×AC sin 120°＝1534，所以AC ＝5，因此BC 2＝AB 2＋AC 2－2AB ·AC ·cos 120°＝9＋25＋2×3×5×12＝49，解得BC ＝7.3．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若a sin A ＋b sin B <c sin C ，则△ABC 的形状是( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不确定解析：选C 根据正弦定理可得a 2＋b 2<c 2.由余弦定理得cos C ＝a 2＋b 2－c22ab<0，故C 是钝角．即△ABC 是钝角三角形．4．已知在△ABC 中，sin A ∶sin B ∶sin C ＝3∶5∶7，那么这个三角形的最大内角的大小为________．解析：由sin A ∶sin B ∶sin C ＝3∶5∶7知，三角形的三边之比a ∶b ∶c ＝3∶5∶7，最大的角为C .由余弦定理得cos C ＝－12，∴C ＝120°.答案：120°5．在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c .已知△ABC 的面积为315，b －c ＝2，cos A ＝－14，则a 的值为________．解析：在△ABC 中，由cos A ＝－14可得sin A ＝154，所以有⎩⎪⎨⎪⎧ 12bc ×154＝315，b －c ＝2，a 2＝b 2＋c 2－2bc ×⎝⎛⎭⎫－14，解得⎩⎪⎨⎪⎧a ＝8，b ＝6，c ＝4.答案：8[练常考题点——检验高考能力]一、选择题 1．在△ABC 中，若sin C sin A ＝3，b 2－a 2＝52ac ，则cos B 的值为( ) A.13 B.12 C.15 D.14解析：选D 由题意知，c ＝3a ，b 2－a 2＝52ac ＝c 2－2ac cos B ，所以cos B ＝c 2－52ac2ac ＝9a 2－152a 26a 2＝14. 2．在△ABC 中，三内角A ，B ，C 的对边分别为a ，b ，c ，面积为S ，若S ＋a 2＝(b ＋c )2，则cos A 等于( )A.45B ．－45 C.1517 D ．－1517解析：选D 由S ＋a 2＝(b ＋c )2，得a 2＝b 2＋c 2－2bc 14sin A －1，由余弦定理可得14sin A－1＝cos A ，结合sin 2A ＋cos 2A ＝1，可得cos A ＝－1517或cos A ＝－1(舍去)．3．在△ABC 中，已知b ＝40，c ＝20，C ＝60°，则此三角形的解的情况是( ) A ．有一解 B ．有两解C ．无解D ．有解但解的个数不确定解析：选C 由正弦定理得b sin B ＝c sin C， ∴sin B ＝b sin Cc ＝40×3220＝3>1.∴角B 不存在，即满足条件的三角形不存在．4．已知△ABC 中，内角A ，B ，C 所对边长分别为a ，b ，c ，若A ＝π3，b ＝2a cos B ，c＝1，则△ABC 的面积等于( )A.32 B.34 C.36 D.38解析：选B 由正弦定理得sin B ＝2sin A cos B ，故tan B ＝2sin A ＝2sin π3＝3，又B ∈(0，π)，所以B ＝π3，又A ＝π3＝B ，则△ABC 是正三角形，所以S △ABC ＝12bc sin A ＝12×1×1×32＝34.5．(2017·渭南模拟)在△ABC 中，若a 2－b 2＝3bc 且sin (A ＋B )sin B＝23，则A ＝( )A.π6B.π3C.2π3D.5π6解析：选A 因为sin (A ＋B )sin B ＝23，故sin C sin B ＝23，即c ＝23b ，则cos A ＝b 2＋c 2－a 22bc ＝12b 2－3bc 43b 2＝6b 243b 2＝32，所以A ＝π6.6．已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且c －b c －a ＝sin Asin C ＋sin B，则B ＝( )A.π6B.π4C.π3D.3π4解析：选C 根据正弦定理a sin A ＝b sin B ＝c sin C ＝2R ，得c －b c －a ＝sin A sin C ＋sin B ＝a c ＋b ，即a 2＋c 2－b 2＝ac ，所以cos B ＝a 2＋c 2－b 22ac ＝12，故B ＝π3.二、填空题7．在△ABC 中，角A ，B ，C 所对的边分别是a ，b ，c ，若c ＝1，B ＝45°，cos A ＝35，则b ＝________.解析：因为cos A ＝35，所以sin A ＝1－cos 2A ＝1－⎝⎛⎭⎫352＝45，所以sin C ＝sin[180°－(A ＋B )]＝sin(A ＋B )＝sin A cos B ＋cos A sin B ＝45cos 45°＋35sin 45°＝7210.由正弦定理b sin B ＝c sin C ，得b ＝17210×sin 45°＝57.答案：578．在△ABC 中，若b ＝2，A ＝120°，三角形的面积S ＝3，则三角形外接圆的半径为________．解析：由面积公式，得S ＝12bc sin A ，代入数据得c ＝2，由余弦定理得a 2＝b 2＋c 2－2bc cos A ＝22＋22－2×2×2cos 120°＝12，故a ＝23，由正弦定理，得2R ＝a sin A ＝2332，解得R ＝2.答案：29．在△ABC 中，a ＝4，b ＝5，c ＝6，则sin 2A sin C＝________. 解析：由正弦定理得sin A sin C ＝a c ，由余弦定理得cos A ＝b 2＋c 2－a 22bc，∵a ＝4，b ＝5，c ＝6，∴sin 2A sin C ＝2sin A cos A sin C ＝2·sin A sin C ·cos A ＝2×a c ×b 2＋c 2－a 22bc ＝2×46×52＋62－422×5×6＝1. 答案：110．在△ABC 中，B ＝120°，AB ＝2，A 的角平分线AD ＝3，则AC ＝________.解析：如图，在△ABD 中，由正弦定理，得AD sin B ＝AB sin ∠ADB， ∴sin ∠ADB ＝22. 由题意知0°<∠ADB <60°，∴∠ADB ＝45°，∴∠BAD ＝180°－45°－120°＝15°.∴∠BAC ＝30°，C ＝30°，∴BC ＝AB ＝ 2.在△ABC 中，由正弦定理，得AC sin B ＝BC sin ∠BAC，∴AC ＝ 6.答案： 6三、解答题11．(2017·河北三市联考)在△ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，且a sin B＝－b sin ⎝⎛⎭⎫A ＋π3. (1)求A ；(2)若△ABC 的面积S ＝34c 2，求sin C 的值． 解：(1)∵a sin B ＝－b sin ⎝⎛⎭⎫A ＋π3， ∴由正弦定理得sin A sin B ＝－sin B sin ⎝⎛⎭⎫A ＋π3，则sin A ＝－sin ⎝⎛⎭⎫A ＋π3，即sin A ＝－12sin A －32cos A ，化简得tan A ＝－33，∵A ∈(0，π)，∴A ＝5π6. (2)∵A ＝5π6，∴sin A ＝12， 由S ＝12bc sin A ＝14bc ＝34c 2，得b ＝3c ， ∴a 2＝b 2＋c 2－2bc cos A ＝7c 2，则a ＝7c ，由正弦定理得sin C ＝c sin A a ＝714. 12．(2017·郑州模拟)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且满足cos 2C－cos 2A ＝2sin ⎝⎛⎭⎫π3＋C ·sin ⎝⎛⎭⎫π3－C . (1)求角A 的值；(2)若a ＝3且b ≥a ，求2b －c 的取值范围．解：(1)由已知得2sin 2A －2sin 2C ＝234cos 2C －14sin 2C ，化简得sin A ＝32，故A ＝π3或2π3. (2)由题知，若b ≥a ，则A ＝π3，又a ＝3， 所以由正弦定理可得b sin B ＝c sin C ＝a sin A＝2，得b ＝2sin B ，c ＝2sin C ， 故2b －c ＝4sin B －2sin C ＝4sin B －2sin ⎝⎛⎭⎫2π3－B ＝3sin B －3cos B ＝23sin ⎝⎛⎭⎫B －π6. 因为b ≥a ，所以π3≤B ＜2π3，π6≤B －π6＜π2， 所以23sin ⎝⎛⎭⎫B －π6∈[3，23)．即2b －c 的取值范围为[3，23).。

第06节 正弦定理和余弦定理班级__________ 姓名_____________ 学号___________ 得分__________一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选择中，只有一个是符合题目要求的。

） 1.【2017浙江台州中学10月】在ABC ∆中，3b =，c =30B =，则a =（ ） A.6 B.3 C.6或3 D.6或4 【答案】C.∴6a =或3，故选C.2.【2018届云南省师范大学附属中学月考一】已知,,,,,a b c A B C 分别是ABC ∆的三条边及相对三个角，满足::cos :cos :cos a b c A B C =，则ABC ∆的形状是（ ）A. 等腰三角形B. 等边三角形C. 直角三角形D. 等腰直角三角形 【答案】B【解析】由正弦定理得： ::::a b c sinA sinB sinC =，又::c o s :c o s :c o s a b c A B C =，所以有tan tan tan A B C ==，即A B C ==，所以ABC ∆是等边三角形，故选B.3.已知ABC ∆中，C B A ∠∠∠,,的对边分别为,,a b c若a c ==75A ∠=o ，则b =（ ）A.2 B ．4＋．4—【答案】A由正弦定理得1sin 2sin 2ab B A=⋅==,故选A4.【2017山东，理9】在C ∆AB 中，角A ，B ，C 的对边分别为a ，b ，c ．若C ∆AB 为锐角三角形，且满足()sin 12cosC 2sin cosC cos sinC B +=A +A ，则下列等式成立的是（A ）2a b = （B ）2b a = （C ）2A =B （D ）2B =A 【答案】A【解析】sin()2sin cos 2sin cos cos sin A C B C A C A C ++=+ 所以2sin cos sin cos 2sin sin 2B C A C B A b a =⇒=⇒=，选A. 5.已知在ABC ∆中，ccb A 22cos2+=，则ABC ∆的形状是( ) A ．直角三角形 B ．等腰三角形或直角三角形 C ．正三角形 D ．等腰直角三角形 【答案】A【解析】由正弦定理得C B c c b sin 2sin 212+=+，∴CBA sin 2sin 212cos 1+=+， ∴C A B sin cos sin =.∵在三角形中有)sin()](sin[sin C A C A B +=+-=π， ∴C A C A C A sin cos sin cos cos sin =+. ∴0cos sin =C A .∵0sin ≠A ，∴0cos =C ，即2π=C . 故ABC ∆为直角三角形．选A.6. ABC ∆中，角C B A ,,所对的边长分别为c b a ,,，b A B c C B a 21cos sin cos sin =+，且b a > ，则B ∠=（ ） A ．6π B ．3πC ．32πD ．65π【答案】A【解析】由正弦定理得1sin sin cos sin sin cos sin 2A B C C B A B +=，即11sin()sin 22A CB +=⇒=，又b a >，6B π∴=。

高中数学：正弦定理和余弦定理练习及答案高中数学：正弦定理和余弦定理练习一、选择题1．在△ABC 中，已知b ＝4，c ＝2，∠A ＝120°，则a 等于……………….( )A ．2B ．6C ．2或6D ．2 2．在△ABC 中，已知三边a 、b 、c 满足(a ＋b ＋c )(a ＋b -c )＝3ab ，则∠C 等于…..( )A ．15°B ．30°C ．45°D ．60°3．已知在△ABC 中，sin A △sin B △sin C ＝3△5△7，那么这个三角形的最大角是…( )A ．135°B ．90°C ．120°D ．150°4．在△ABC 中，若c 4-2(a 2＋b 2)c 2＋a 4＋a 2b 2＋b 4＝0，则△C 等于………………….( )A ．90°B ．120°C ．60°D ．120°或60°5．已知A 、B 、C 是△ABC 的三个内角，则在下列各结论中，不正确的为………...( )A ．sin 2A ＝sin 2B ＋sin 2C ＋2sin B sin C cos(B ＋C )B ．sin 2B ＝sin 2A ＋sin 2C ＋2sin A sin C cos(A ＋C )C ．sin 2C ＝sin 2A ＋sin 2B -2sin A sin B cos CD ．sin 2(A ＋B )＝sin 2A ＋sin 2B -2sin B sin C cos(A ＋B )6*．在△ABC 中，AB ＝5，BC ＝7，AC ＝8，则的值为……………………( )A ．79B ．69C ．5D ．-5二、填空题7．已知△ABC 中，A ＝60°，最大边和最小边是方程x 2-9x ＋8＝0的两个正实数根，那么BC 边长是________．8．在△ABC 中，已知a ＝7，b ＝8，cos C ＝，则最大角的余弦值是________．3321213615+?14139．在△ABC 中，△C ＝60°，a 、b 、c 分别为△A 、△B 、△C 的对边，则＝________．10*．在△ABC 中，若AB ＝，AC ＝5，且cos C ＝，则BC ＝________．三、解答题11．已知a ＝3，c ＝2，B ＝150°，求边b 的长及S △．12．在△ABC 中，cos2，c ＝5，求△ABC 的内切圆半径．13．已知△ABC 的三边长a 、b 、c 和面积S 满足S ＝a 2-(b -c )2，且b ＋c ＝8，求S 的最大值．ca b c b a +++5109310922=+=c c b A14*．已知a 、b 、c 为△ABC 的三边，且a 2-a -2b -2c ＝0，a ＋2b -2c ＋3＝0，求这个三角形的最大内角．§1.1.2正弦定理和余弦定理参考答案一、选择题A D C D D D二、填空题7． 8．- 9．1 10．4或5三、解答题11．解：b 2＝a 2＋c 2-2ac cos B ＝(3)2＋22-2·2·2·(-)＝49．△ b ＝7，S △＝ac sin B ＝×3×2×＝．12．解：△ c ＝5，，△ b ＝4 又cos 2 △ cos A ＝又cos A ＝△△ b 2＋c 2-a 2＝2b 2△ a 2＋b 2＝c 2 5771332321213212331092=+c c b c c b A A 22cos 12+=+=c b bc a c b 2222-+c b bc a c b =-+2222△ △ABC 是以角C 为直角的三角形．a ＝＝3△ △ABC 的内切圆半径r ＝(b ＋a -c )＝1．13．解：△ S ＝a 2-(b -c )2 又S ＝bc sin A △ bc sin A ＝a 2-(b -c )2△ (4-sin A )△ cos A ＝(4-sin A )△ sin A ＝4(1-cos A )△ 2sin △ tan △ sin A＝△ c ＝b ＝4时，S 最大为 14．解：△ a 2-a -2b -2c ＝0，a ＋2b -2c ＋3＝0由上述两式相加，相减可得c ＝(a 2＋3)，b ＝(a -3)(a ＋1)△ c -b ＝(a ＋3)△ a ＋3＞0，△ c ＞bc -a ＝(a 2＋3)-a ＝(a 2-4a ＋3)＝(a -3)(a -1) △ b ＝(a -3)(a ＋1)＞0，△ a ＞3△ (a -3)(a -1)＞0△ c ＞a△ c 边最大，C 为最大角 22b c -212121412222=-+bc a c b 412sin 82cos 22A A A =2A 41=178)41(14122tan 12tan 222=+?=+A A17644)(174174sin 212=+?≤==c b S bcA bC S Θ17644141214141414141△ cos C ＝△ △ABC 的最大角C 为120°ab c b a 2222-+21)1)(3(412)3(161)1()3(16122222-=+-?+-+-+ =a a a a a a a。