零极点分析和频谱分析

课程设计报告课程名称数字信号课程设计系别：工程技术系专业班级：电子信息工程0901学号：**姓名：**课程题目：离散系统的频域分析与零极点分布完成日期：2012年6月29日指导老师：**2012 年6 月29 日离散系统的频域分析与零极点分布摘要本课题主要是根据系统函数求出系统的零极点分布图并且求解系统的单位脉冲响应,利用MATLAB软件绘制出系统零极点的分布图,根据零极点在单位圆的分布,判断因果系统的稳定性.再比较不同零极点对系统频率响应特性的影响。

从课题研究和设计过程当中对系统稳定性的判断有了清楚的认识,既极点在单位圆内,则该系统稳定,极点在单位圆外，则该系统为非稳定系统。

同时也对系统函数零极点分布对系统频率响应特性的影响有了深入的了解。

既极点位置主要影响频率响应的峰值及尖锐程度,零点位置主要影响频率响应的谷点位置及形状。

本次课题也对系统的幅频特性曲线和相频特性曲线进行了绘制,并求出了系统的单位脉冲响应以及绘制出了波形图。

关键字：离散系统，频域分析，零极点分布目录一、绪论 (1)二、方案 (1)实验原理 (1)三、过程论述及结果分析 (2)1.分别画出各系统的零极点分布图，并判断系统的稳定性 (2)2.分别画出系统的幅频特性和相频特性曲线 (5)3.分别求出系统的单位脉冲响应，并画出其波形 (9)四、结论 (12)致谢 (13)参考文献 (13)一、绪论编制Matlab 程序，完成以下功能，根据系统函数求出系统的零极点分布图，并求解系统的单位脉冲响应；根据零极点分布图判断系统的稳定性；比较不同零极点发布对系统频率响应特性的影响；绘制相关信号的波形。

具体要求如下：下面四种二阶网络的系统函数具有相同的极点发布：1121()1 1.60.9425H z z z --=-+121210.3()1 1.60.9425z H z z z ----=-+131210.8()1 1.60.9425z H z z z ----=-+ 124121 1.60.8()1 1.60.9425z z H z z z-----+=-+ （1）分别画出各系统的零极点分布图，并判断系统的稳定性； （2）分别画出系统的幅频特性和相频特性曲线； （3）分别求出系统的单位脉冲响应，并画出其波形。

频谱分析方法频谱分析方法是在设备故障诊断中最常使用的方法。

常用的频谱是功率普和幅值谱。

功率谱表示振动功率随振动频率进行分布的情况，物理意义比较清楚；幅值谱表示对应于各频率的谐波振动分量所具有的振幅，应用时比较直观。

幅值谱上谱线高度就是该频率分量的振幅大小。

频谱分析的目的就是将构成信号的各种频率成分都分解开来，以便于识别振源。

1.进行频谱分析首先要了解频谱的构成成分，依据故障的推理方式的不同，对频谱的构成成分的了解可按不同的层次进行。

（1）. 按高、中、低三个频段进行分析，初步了解主故障发生的部位；（2）. 按：工频、超谐波、次谐波、进行分析，用以确定故障的范围：对中、平衡、松动类故障均与工频（也称：基频、转频）的整数倍或分数倍有着密切的关联；（3）. 按频率成分的来源进行分析。

如：零部件共振的频率成分、随机噪声干扰成分、非线性调制生成的和差频成分等等；（4）. 按特征频率进行分析。

振动特征频率是各振动零部件有故障时必定产生的的频率成分。

如：不平衡必定产生工频，气流在叶片间流动必定产生通过频率，齿轮啮合时有啮合频率，过临界转速时有共振频率，零部件受冲击时会被激发出固有频率等等。

2. 对主振成分进行频谱分析时，首先要关注幅值较高的谱峰，因为其量值对振动的总水平影响较大。

如：工频成分突出，往往是不平衡所致，要加以区别的是轴弯曲、共振、角不对中、基础松动、定/转子同心度不良等故障。

2倍频为平行不对中、转轴有横裂纹。

（0.42～0.48）倍频过大，为涡动失稳。

（0.5～0.8）倍频是流体旋转脱离。

特低频是喘振。

整数倍频是叶片故障。

啮合成分高是齿轮表面接触不良。

谐波丰富是松动。

边频是调制。

分频是流体激振、摩擦等等。

3. 做频谱对比发现异常时、在分析和诊断过程时应注意从它们的发展变化（趋势）中得出准确的结论,单独一次测量往往很难对故障做出准确的判断。

有些振动成分虽然较大，但很平稳、不随时间变化，对机器运行不构成威胁。

（一）离散时间信号的Z 变换1．利用MATLAB 实现z 域的部分分式展开式MATLAB 的信号处理工具箱提供了一个对F(Z)进行部分分式展开的函数residuez()，其调用形式为：[r,p,k]=residuez(num,den)式中，num 和den 分别为F(Z)的分子多项式和分母多项式的系数向量，r 为部分分式的系数向量，p 为极点向量，k 为多项式的系数向量。

【实例1】 利用MATLAB 计算321431818)(-----+zz z z F 的部分分式展开式。

解：利用MATLAB 计算部分分式展开式程序为% 部分分式展开式的实现程序num=[18];den=[18 3 -4 -1];[r,p,k]=residuez(num,den)2．Z 变换和Z 反变换MATLAB 的符号数学工具箱提供了计算Z 变换的函数ztrans()和Z 反变换的函数iztrans （），其调用形式为)()(F iztrans f f ztrans F ==上面两式中，右端的f 和F 分别为时域表示式和z 域表示式的符号表示，可应用函数sym 来实现，其调用格式为()A sym S =式中，A 为待分析的表示式的字符串，S 为符号化的数字或变量。

【实例2】求（1）指数序列()n u a n 的Z 变换;(2)()()2a z az z F -=的Z 反变换。

解 （1）Z 变换的MATLAB 程序% Z 变换的程序实现f=sym('a^n');F=ztrans(f)程序运行结果为：z/a/(z/a-1)可以用simplify( )化简得到 :-z/(-z+a)（2）Z 反变换的MATLAB 程序% Z 反变换实现程序F=sym('a*z/(z-a)^2');f=iztrans(F)程序运行结果为f =a^n*n（二）系统函数的零极点分析1. 系统函数的零极点分布离散时间系统的系统函数定义为系统零状态响应的z 变换与激励的z 变换之比，即)()()(z X z Y z H = （3-1）如果系统函数)(z H 的有理函数表示式为：11211121)(+-+-++++++++=n n n n m m m m a z a z a z a b z b z b z b z H （3-2） 那么，在MATLAB 中系统函数的零极点就可通过函数roots 得到，也可借助函数tf2zp 得到，tf2zp 的语句格式为：[Z,P,K]=tf2zp(B,A)其中，B 与A 分别表示)(z H 的分子与分母多项式的系数向量。

傅里叶变换的零极点傅里叶变换的零极点【前言】在信号处理和数学领域，傅里叶变换是一种重要的工具。

通过傅里叶变换，我们可以将一个时域信号转换为频域信号，从而更好地理解信号的特性和频谱分布。

然而，在深入研究傅里叶变换过程中，我们会遇到一个重要的概念——零极点。

零极点在傅里叶变换中起着关键作用，帮助我们理解信号的频率响应以及系统的稳定性。

本文将从简单到复杂的角度，探讨傅里叶变换的零极点，以帮助读者更深入地理解这一概念。

【一、什么是零极点】在傅里叶变换中，我们经常会遇到有理多项式的形式，例如：H(z) = (z - z1)(z - z2)...(z - zn)/(p1 - z)(p2 - z)...(pm - z)其中，z1, z2,..., zn为多项式的零点，p1, p2,..., pm为多项式的极点。

在复平面上，零点表示系统的频率响应为零的位置，而极点表示系统的频率响应无穷大的位置。

【二、零极点与频率响应】通过傅里叶变换的零极点分析，我们可以了解信号或系统的频率响应特性。

具体来说，零点和极点决定了系统的频域特性和稳定性，从而决定了信号在不同频率下的衰减或增强程度。

1. 零点与频率响应当系统的传递函数H(z)中存在一个零点z0时，系统的频率响应在该频率附近会拥有一个极大值。

也就是说，在这个频率下，信号会被增强。

相反地，如果零点为负数，系统的频率响应将在该频率下降到零。

零点可以决定信号的频域特性，进而影响信号的传输和处理。

2. 极点与系统稳定性极点的位置对于系统的稳定性至关重要。

如果极点位于单位圆内，系统将是稳定的。

这意味着，系统对于输入信号的响应将是有界且有限的，不会出现不稳定行为。

相反地，如果极点位于单位圆外，系统将是不稳定的，可能会出现振荡或发散行为。

通过观察极点的位置，我们可以判断系统的稳定性，从而提前预测系统的行为。

【三、零极点分布与系统特性】在实际情况下，零极点的分布对于系统的特性以及频率响应有着重要的影响。

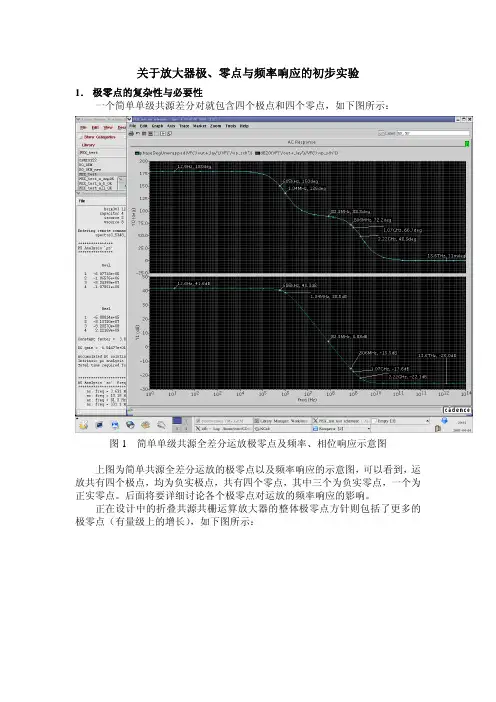
关于放大器极、零点与频率响应的初步实验1．极零点的复杂性与必要性一个简单单级共源差分对就包含四个极点和四个零点，如下图所示：图1 简单单级共源全差分运放极零点及频率、相位响应示意图上图为简单共源全差分运放的极零点以及频率响应的示意图，可以看到，运放共有四个极点，均为负实极点，共有四个零点，其中三个为负实零点，一个为正实零点。

后面将要详细讨论各个极零点对运放的频率响应的影响。

正在设计中的折叠共源共栅运算放大器的整体极零点方针则包括了更多的极零点（有量级上的增长），如下图所示：图2 folded-cascode with gain-boosting and bandgap all-poles details图3 folded-cascode with gain-boosting and bandgap all-zeros details从上述两张图可以看到，面对这样数量的极零点数量（各有46个），精确的计算是不可能的，只能依靠计算机仿真。

但是手算可以估计几个主要极零点的大致位置，从而预期放大器的频率特性。

同时从以上图中也可以看到，详细分析极零点情况也是很有必要的。

可以看到46个极点中基本都为左半平面极点（负极点）而仿真器特别标出有一个正极点（RHP ）。

由于一般放大器的极点均应为LHP ，于是可以预期这个右半平面极点可能是一个设计上的缺陷所在。

（具体原因现在还不明，可能存在问题的方面：1。

推测是主放大器的CMFB 的补偿或者频率响应不合适。

2。

推测是两个辅助放大器的带宽或频率响应或补偿电容值不合适）其次可以从极零点的对应中看到存在众多的极零点对（一般是由电流镜产生），这些极零点对产生极零相消效应，减少了所需要考虑的极零点的个数。

另外可以看到46个零点中45个为负零点，一个为正零点，这个正零点即是需要考虑的对放大器稳定性产生直接影响的零点。

以上只是根据仿真结果进行的一些粗略的分析，进一步的学习和研究还需要进行一系列实验。

电路中零极点
在电路分析中，零极点是描述电路频率特性的重要概念。

零点是指系统函数在某个特定频率处的值为零的点，而极点则是系统函数在某个特定频率处的一阶导数为零的点。

在分析电路的频率响应时，零极点可以提供重要的信息，包括系统的稳定性、增益和相位等。

在电路中，零极点的存在会影响系统的频率响应。

具体来说，一个电路系统的传递函数可以表示为一系列的零点和极点的形式。

当输入信号的频率接近零点或极点时，系统的输出信号会受到较大的影响，可能会产生幅度跳跃、相位失真等现象。

因此，通过分析电路中的零极点，可以了解系统在不同频率下的响应特性，从而优化电路设计。

在分析电路中的零极点时，通常需要使用电路分析方法和数学工具。

例如，使用交流等效电路分析方法可以得到系统函数的具体形式，然后根据数学工具求解零极点的位置。

此外，还可以使用计算机仿真软件进行电路的频域分析和参数优化。

综上所述，零极点是描述电路频率特性的重要概念，通过分析零极点的位置和特性，可以深入了解电路在不同频率下的响应特性，优化电路设计，提高系统的性能。

《数字信号处理A 》实验报告实验三 实验名称：离散系统的频率响应分析和零、极点分布专业及班级：电子131 姓名：XXX 学号：XXXXXX一、实验目的加深对离散系统的频率响应分析和零、极点分布的概念理解。

二、实验步骤（附源代码及仿真结果图）求如下系统的零、极点和幅度频率响应和相位响应。

54321543212336.09537.08801.14947.28107.110528.0797.01295.01295.00797.00528.0)(-----------+-+-+++++=z z z z z z z z z z z H 零点与极点：num=[0.0528 0.0797 0.1295 0.1295 0.797 0.0528]; den=[1 -1.8107 2.4047 -1.8801 0.9537 -0.2336];[z,p,k]=tf2zp(num,den);% 求得有理分式形式的系统转移函数的零、极点 disp('零点');disp(z); %显示矩阵 disp('极点');disp(p); disp('增益系数');disp(k);sos=zp2sos(z,p,k);% 将高阶系统分解为2阶系统的串联 disp('二阶节');disp(real(sos));zplane(num,den)% 直接绘出有理分式形式的系统转移函数的零、极点分布图零点：-1.5870 + 1.4470i -1.5870 - 1.4470i0.8657 + 1.5779i 0.8657 - 1.5779i -0.0669 极点：0.1984 + 0.9076i 0.1984 - 0.9076i 0.4431 + 0.5626i 0.4431 - 0.5626i 0.5277 增益系数： 0.0528 二阶节：0.0528 0.0035 0 1.0000 -0.5277 0 1.0000 3.1740 4.6125 1.0000 -0.8862 0.51291.0000 -1.7315 3.2392 1.0000 -0.3968 0.8631 极点图如下图所示：-2-1.5-1-0.500.511.5-1.5-1-0.50.511.5Real PartI m a g i n a r y P a r t幅度频率响应和相位响应：k=255;num=[0.0528 0.0797 0.1295 0.1295 0.797 0.0528];den=[1 -1.8107 2.4047 -1.8801 0.9537 -0.2336];w=0:pi/k:pi;h=freqz(num,den,w);% 系统的频率响应，w是频率的计算点subplot(2,2,1);plot(w/pi,real(h));gridtitle('实部')xlabel('\omega/\pi');ylabel('幅度')subplot(2,2,2);plot(w/pi,imag(h));gridtitle('虚部')xlabel('\omega/\pi');ylabel('Amplitude')subplot(2,2,3);plot(w/pi,abs(h));gridtitle('幅度谱')xlabel('\omega/\pi');ylabel('幅值')subplot(2,2,4);plot(w/pi,angle(h));gridtitle('相位谱')xlabel('\omega/\pi');ylabel('弧度')0.51-50510实部ω/π幅度0.51-10-505虚部ω/πA m p l i t u d e0.5102468幅度谱ω/π幅值0.51-4-2024相位谱ω/π弧度三、总结与体会通过这次实验，加深了使我对MATLAB 软件的熟练程度，并且加深了对离散系统的频率响应分析和零、极点分布的概念理解，对课本上知识的回顾让我更加的理解并且掌握，对于幅度频率谱和相位谱的有了更深的理解，只要把实验的例题弄懂那么实验其实也不是很难，就跟公式一样，万变不离其宗，变化的是参数，这次实验真的体会到了很多东西。

实验3 离散系统的频率响应分析和零、极点分布实验目的：加深对离散系统的频率响应分析和零、极点分布的概念理解。

加深对离散系统的频率响应分析和零、极点分布的概念理解。

实验原理：离散系统的时域方程为离散系统的时域方程为åå==-=-M k k N k k k n x p k n y d00)()(其变换域分析方法如下：其变换域分析方法如下：频域频域 )()()(][][][][][w w w j j j m e H e X e Y m n h m x n h n x n y =Û-=*=å¥-¥= 系统的频率响应为系统的频率响应为 w w ww w w w jN N j jM M j j j j e d e d d e p e p p e D e p e H ----++++++==......)()()(1010 Z 域 )()()(][][][][][z H z X z Y m n h m x n h n x n y m =Û-=*=å¥-¥=系统的转移函数为系统的转移函数为N N M M z d z d d z p z p p z D z p z H ----++++++==......)()()(110110 分解因式分解因式Õ-Õ-=åå==-=-=-=-N i i M i i N i i k M i i k z z K z d zp z H 111100)1()1()(l x ，其中i x 和i l 称为零、极点。

点。

在MATLAB 中，可以用函数中，可以用函数[z [z [z，，p ，K]=tf2zp K]=tf2zp（（num num，，den den）求得有理分式形式的）求得有理分式形式的系统转移函数的零、极点，用函数zplane zplane（（z ，p ）绘出零、极点分布图；也可以用函数zplane zplane（（num num，，den den）直接绘出有理分式形式的系统转移函数的零、极）直接绘出有理分式形式的系统转移函数的零、极点分布图。