当前位置：文档之家 › 第4讲_5.5奈奎斯特稳定判据

第4讲_5.5奈奎斯特稳定判据

  • 格式：ppt
  • 大小：1.03 MB
  • 文档页数：27

下载文档原格式

  / 27

合集下载

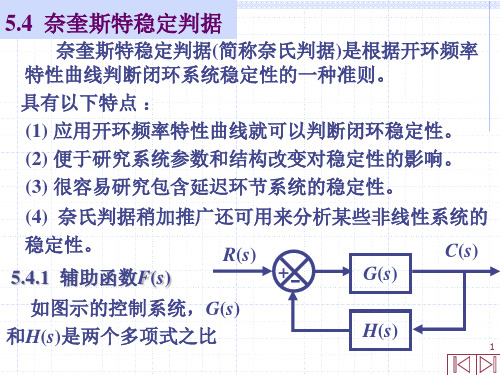
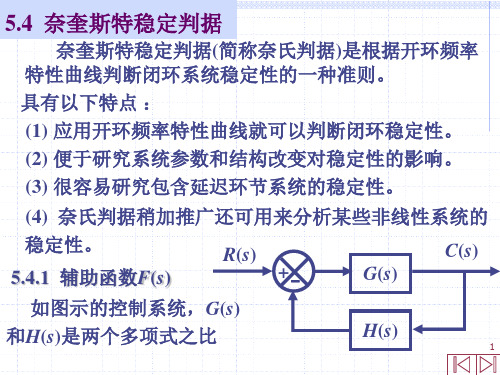
52奈氏判据

52奈氏判据
5.4 奈奎斯特稳定判据
奈奎斯特稳定判据(简称奈氏判据)是根据开环频率 特性曲线判断闭环系统稳定性的一种准则。
具有以下特点 ：
(1) 应用开环频率特性曲线就可以判断闭环稳定性。
(2) 便于研究系统参数和结构改变对稳定性的影响。
(3) 很容易研究包含延迟环节系统的稳定性。
(4) 奈氏判据稍加推广还可用来分析某些非线性系统的
14
例5-11 一单位反馈系统，其开环传函
k Gk (s) Ts 1 试用奈氏判据判断系统的稳定性。
解：已知 p = 1
频率特性
Gk ( j )
k
jT 1
kT
j 1 / T
当 = 0，Gk (j0) = k180
当 ，Gk (j) = 090
Im
k
=0
0
Re
15
k
=0
1
Im
0
Re
当 k < 1时 ，R = 1/2
270
arctan
(T1 1
T2 ) 2T1 T2
当() = 180时，g =(1/T1T2)1/2 ，A(g)=kT2
③ 稳定性判别。 G(s)H(s)有一个积分环节 =1 ，故
补画了180到270的辅助线。
26
L()/dB
G(s)H(s) k(T2s 1)
20dB/dec 40dB/dec
(s) G(s)
M1(s)N2(s)
1 G(s)H(s) N1(s)N2(s) M1(s)M2(s)
把闭环特征多项式和开环特征多项式之比称之为辅 助函数， 记作F(s)， F(s)仍是复变量s的函数。
F(s)
DB (s) Dk (s)

52奈氏判据

52奈氏判据
10
例5-10 判断系统稳定性 解：由图知 （1）p = 0 且 R = 0 闭环系统是稳定的。
Im
Im
0
= 0 Re
p=0
1 0
Re
= 0
（2） p = 0 ，R 2
z p R 2 0 闭环系统不稳定的。
p=0
11
Im
1
0
= 0
Re
p=0
（3） p = 0 ，R 0 闭环系统是稳定的。
Gk (
j )
(1
k
(T1 )2 )(1
(T2 )2 ) [(T1
T2 )
j
1 2T1T2
]
令虚部=0，得，
2 x
1 T1T2
Re(
x
)
kT1T2 T1 T2
17
系统的开环极坐标图如图示：
所作的增补线如虚线所示。
=0-
当 kT1T2 1 T1 T2
R=2 z = p R = 2
面，开环系统临界稳定。在这种情 0
况下，不能直接应用奈氏判据。
0
如果要应用奈氏判据，可把零根视为稳定根。因此，
在数学上作如下处理：在平面上的s=0邻域作一半径无
穷小的半圆，绕过原点。
相应地，在GH平面上开环极坐标图在 =0时，小
半圆映射到GH平面上是一个半径为无穷大，从= 0到
= 0+顺时针旋转N • 180° 的大圆弧。如此处理之后，
(s) G(s)
M1(s)N2(s)
1 G(s)H(s) N1(s)N2(s) M1(s)M2(s)
把闭环特征多项式和开环特征多项式之比称之为辅 助函数， 记作F(s)， F(s)仍是复变量s的函数。

5.5Nyquist稳定判据

5.5Nyquist稳定判据

由于F（jw）与 G（jw）H（jw）这两个矢量之间相差1，
所以可以直接用系统开环的Nyquist轨迹来判断稳定性。
4、总结：
Nyquist稳定判据（系统稳定的充要条件）
①系统开环稳定，G j H j Nyquist曲线 不包围 1, j 0 点，系统闭环后稳定。 ②若系统开环不稳定，有q个特征根都在S
N S S 2n S n S p1 S p2 0
2 2
① 1 A
稳 定 1 状 2 态 p p1 2

Im
不 稳 j j 定 1 Re 状 2 0 0 p p2 1 态

2
Im
B
Re

N j 2
:0

A 20 1 2 1 (2 ) 2 1 (5 ) 2
0 tg 1 tg 1 2 tg 1 5
A 0 20 A 0
0 0 270
四、“穿越”与系统稳定性的判 定 （1）

2
:0
称米哈伊洛夫稳定定理
二、Nyquist稳定判据
1、开环特征方程式与闭环特征方程式的关系
FS 1 GSHS
F
KNS 令 G SHS DS
S
D S KN DS
S
DB DK
S S
K1 S S1 S S 2 S S n K 2 S p1 S p2 S pn
2
③无论开环稳定或不稳定，若闭环不稳定， 则系统闭环后在右半平面根的个数为Z ,则
Z q 2 N q 2( N N )
N ：开环 Nyquist曲线在实轴 (,1) 段的正 穿越次数， N 负穿越次数。

奈氏判据

奈氏判据
1
0
KT
2

Re
1 0
Re
0
稳定
(a) KT 1 时N 0
2
0
图4-41 例11奈氏曲线
不稳定
(b) KT 1 时N 2
2
18
练习 已知反馈控制系统的开环传递函数为
K G(s)H(s)
s(T1s 1)(T2s 1)
方向包围 F(s)平面原点的次数，等于封闭曲线
L内s 包含F(s)的极点数P与零点数Z之差。即
N PZ
(4-30)
若N>0，则LF 按逆时针方向绕F(s)平面坐标原点N周；
若N<0，则LF 按顺时针方向绕 F(s)平面坐标原点N周；
若N=0，则LF 不包围F(s)平面坐标原点。
9
z n 1
z3
13
2.当系统开环传递函数 G(s)H有(sp)个位于S平面右半部的极
点时，如果系统的奈氏曲线 LG逆H 时针包围 (1点, j的0) 周数等
于位于S平面右半部的开环极点数(N=P)，则闭环系统是稳 定的(Z=P-N=0),否则是不稳定的；
3. 如果系统的奈氏曲线 LGH顺时针包围点 (1, j0)
上的虚线看成对数相频特性的一部分。
26
第六节 系统的相对稳定性
在工程应用中，由于环境温度的变化、元件的老化以及元件 的更换等，会引起系统参数的改变，从而有可能破坏系统的稳 定性。因此在选择元件和确定系统参数时，不仅要考虑系统的 稳定性，还要求系统有一定的稳定程度，这就是所谓自动控制 系统的相对稳定性问题。
对数相频特性的-180o(2k+1)线
对数相频曲线中由下向上 穿越-180o(2k+1)线 为正 对数相频曲线中由上向下穿越-180o(2k+1)线 为负

奈奎斯特稳定判据

奈奎斯特稳定判据

二、控制系统的频域稳定性判据

3. n阶系统 n阶系统稳定的充要条件是当ω由0→∞时， 特征矢量D(jω)的相角变化量为 Δ Arg[D(jω)]= n² 90 °
奈奎斯特稳定判据
三、奈奎斯特判据（奈氏判据） 1. 0型系统（开环没有串联积分的系统）

⑴开环是稳定的系统
如果已知开环系统是稳定的，那么当ω由0→∞时， 若矢量F(j ω)的相角变化量为0，也就是F(j ω)的轨迹不包 围原点，那么闭环系统的特征方程式DB(s)的根全部在s 左半平面，系统是稳定的。否则，系统是不稳定的。 这样，系统稳定问题转化为找出ω由0→∞时，矢量 F(j ω)的相角变化量问题。
奈奎斯特稳定判据

四、伯德图上的稳定性判据 奈氏判据除了可以表示在极坐标图上， 还可以表示在伯德图上。
w + w=+ w=0 -1 P=0 w
0
180

-
+
四、伯德图上的稳定性判据

由图可知，幅相曲线不包围（-1，j0）点。 此结果也可以根据ω增加时，幅相曲线自下 向上（幅角减小）和自上向下（幅角增加） 穿越实轴区间（-∞，-1）的次数决定。
如果把自上向下的穿越称为正穿越，正穿越次 数用N+表示。把自下向上的穿越称为负穿越，负 穿越次数用N-表示，则R可以用N+和N-之差确定， 即 R= N+- N-

由图可知， N+=1， N-=1，故R=0。
四、伯德图上的稳定性判据
1.Bode图与Nyquist图的对应关系 a. Nyquist图的单位圆 | G(j )H(j ) | 1 对应 Bode图的横轴 20lg | G(j )H(j ) | 0 b. | G(j )H(j ) | 1 单位圆外 对应 20lg| G(j )H(j ) | 0 横轴以上区域

2第3、4、5、6节奈魁斯特稳定判据

2第3、4、5、6节奈魁斯特稳定判据

2
5.3.1 完整的频率特性极坐标图 R(s) + -
G(s)
H(s)
C(s)
闭环传递函数
C s Gs s Rs 1 Gs H s
KN s 开环传递函数 G s H s s Ds N 0 D0 1, 为串联积分环节个数 K 0 为放大系数

对含有积分环节的开环传递函数，当 s由 j j0 j0 j 变化时，也称 由 0 连续变化。 Tuesday, June 16, 2015
8
Tuesday, June 16, 2015
9
5.3.2 奈奎斯特稳定判据 可用复变函数中的幅角定理证明奈奎斯特稳定判据
Tuesday, June 16, 2015
22
开环频率特性的极坐标图在点(-1,j0)左方正、负穿越 负实轴的次数，对应于伯德图上，在开环对数幅频特性 大于0dB的频段内，相频特性曲线正穿越（相位增加） 和负穿越（相位减少） 180 线的次数。 根据伯德图分析闭环系统稳定性的奈奎斯特稳定判据： 闭环系统稳定的充要条件是，在开环幅频特性大于0dB 的所有频段内，相频特性曲线对 180 线的正、负穿越 次数之差等于P/2，其中P为开环正实部极点个数。 当开环系统含有积分环节时，相频特性应增补 由 0 0 的部分。
● 闭环系统的开环传递函数存在正实部极点的情况
奈奎斯特稳定判据的表述1： 若闭环系统的开环传递函数 Gs H s 有P个正实部极 点，则闭环系统稳定的充要条件是，当s按顺时针方 向沿奈奎斯特围线连续变化一周时， Gs H s 绘出的 封闭曲线应按逆时针方向包围点（－1，j0）P周。
Tuesday, June 16, 2015

乃奎斯特稳定判据


一样，对于s平面上任意一条不经过F(s)任何奇异点旳封闭 曲线 s，也可在F(s)平面上找到一条与之相相应旳封闭曲线 f （为 s旳映射）。
[例]辅助方程为：F (s) s 2
s
，则s平面上 ds点（-1，j1），映射
到F(s)平面上旳点d f为（0，-j1）,见下图：
ds (1, j1)
s平面
乃奎斯特稳定判据
1
主要内容
幅角定理 乃奎斯特稳定判据 乃氏稳定判据在Ⅰ、Ⅱ 型系统中旳应用 在波德图上鉴别系统稳定性
乃奎斯特稳定判据是用开环频率特征鉴别闭环系统旳稳 定性。不但能判断系统旳绝对稳定性，而且可根据相对稳定 旳概念，讨论闭环系统旳瞬态性能，指出改善系统性能旳途 径。
2
一、幅角定理：
设负反馈系统旳开环传递函数为：Gk (s) G(s)H (s) ，其 中：G(s)为前向通道传递函数，H (s)为反馈通道传递函数。
7
二、乃奎斯特稳定判据： 对于一种控制系统，若其特征根处于s右半平面，则系统是
不稳定旳。对于上面讨论旳辅助方程 F (s) 1 Gk (s) ，其零点恰 好是闭环系统旳极点，所以，只要搞清F(s)旳旳零点在s右半平 面旳个数，就能够给出稳定性结论。假如F(s)旳右半零点个数为 零，则闭环系统是稳定旳。
当已知开环右半极点数时，便可由N判断闭环右极点数
8
完毕这个设想需要处理两个问题：
1、怎样构造一种能够包围整个s右半平面旳封闭曲线，而且它是 满足柯西幅角条件旳？
2、怎样拟定相应旳映射F(s)对原点旳包围次数N。并将它和开环 频率特征GH ( j)相联络？
第1个问题：先假设F(s)在虚轴上没有零、极点。按顺时针方向
22
射；
③ 以 s = j 代入F(s)，令从－∞→0 ，得第三部分旳映射。

奈奎斯特稳定性判据 ppt课件


24
三、例题详解
【解答】 (1)
半奈奎斯特曲线
K (1 j ) 1.1 1 0.1 2 G( j ) H ( j ) K jK 2 j ( j0.1 1) (1 0.01 ) (1 0.01 2 )
幅值变化： A(0 ) , A() 0 相角变化： K : 180
时，可应用对数频率特性稳定性判据，判定系统的 稳定性。基于Bode图和基于Nyquist图的两种稳定性 判据是一致的，只是坐标系不同而已。 负反馈闭环系统，位于右半s平面极点的个数为 (3)
9
二、对数频率特性稳定性判据
式中：P —开环传递函数位于右半s平面极点的个 数； N —相频特性曲线正穿越次数。在 L( ) 0 ( ) 自下而上穿越 对应的频率范围内， (2k 1) 180 线的次数，其中自下而上起 始于或终止于该线的次数，折半计算； N —相频特性曲线负穿越次数。在 L( ) 0 ( ) 自上而下穿越 对应的频率范围内， (2k 1) 180 线的次数，其中自上而下起 始于或终止于该线的次数，折半计算； Z —闭环传递函数，位于右半s平面极点的 个数，即特征方程位于右半s平面根的 10 个数。
18
三、例题详解
【解答】
19
三、例题详解
【解答】
20
三、例题详解
【例3】 某负反馈控制系统，开环传递函数
试：（1）画出幅相特性曲线；（2）判定稳定性。
21
三、例题详解
【解答】 (1)
幅相特性曲线
K (T1 T2 ) 1 2TT 1 2 G( j ) H ( j ) j (1 2T12 )(1 2T22 ) (1 2T12 )(1 2T22 )

54-5 奈奎斯特稳定性判据

P183
曲线Γs包围一个F(s)的极点，当S1沿Γs顺时针连续变化一周，
因为Pi映射到F(s)上是在无穷远，因此ΓF逆时针绕F平面零点一周，
(S+Pi)的相角积累是-2π角度。 幅角原理：设F(s)除平面上的有限个奇点外，为单值解析函
数，若S平面上任选一条封闭曲线Cs以顺时针方向包围F(s)的Z 个零点和P个极点，且使它不通过F(s)的奇点，则其在F(s)平面 上的映射曲线CF将围绕着坐标原点旋转N周，其中N=Z-P。 当N>0，表示曲线CF以顺时针方向旋转；
G( s ) K s(T1 s 1)(T2 s 1)
G( j 0) 0
解：依题有 G( j 0 ) 90
G( j) 0 270
K1 (小)
N 0
(稳定)
K
Z P N 00 0
K 2 (大)
N 2
(不稳定)
Z P N 02 2
2)T1 T2，G( j ) H ( j )曲线穿过 (1, j 0)点，说明闭环系统 有一对虚根，闭环系统 不稳定 ；
3) T1 T2，Z N 说明闭环系统有两个极点 P 2 0 2，
右方，故闭环系统不稳定。 在S平面的
例7：已知单位反馈系统开环传递函数,分析系统稳定性。
zdkzcjlueducn22855频域稳定判据系统稳定的充要条件全部闭环极点均具有负的实部由闭环特征多项式系数不解根判定系统稳定性不能研究如何调整系统结构参数来改善系统稳定性及性能代数稳定判据routh判据由开环频率特性直接判定闭环系统的稳定性可研究如何调整系统结构参数改善系统稳定性及性能问题频域稳定判据nyquist判据对数稳定判据
-j∞
G( jω )

2第3、4、5、6节奈魁斯特稳定判据


系统闭环稳定
Monday, June 15, 2020
系统闭环不稳定 18
[例]系统开环传递函数：G(s)H s K s 1， s并2Ts 1
给出 T 和时T 的 开环极坐标图，判断闭环系统的稳定性。
[解]开环传递函数无正实部极点，P=0。
系统闭环稳定
Monday, June 15, 2020
奈奎斯特稳定判据的表述3： 闭环系统稳定的充要条件是，当 由 0 0时，开环奈 奎斯特图应当按逆时针方向包围点(-1,j0)P/2周，P是 开环传递函数正实部极点的个数。
Monday, June 15, 2020
11
● 开环稳定系统（P=0）的奈奎斯特稳定判据： 若开环稳定，闭环稳定的充要条件是，当 由 变化时，增补完整的开环频率特性极坐标图不包围点 (-1,j0)。
Monday, June 15, 2020
16
GsH起s始 于负实轴上，或终止于负实轴时，穿越次
数定义为1/2次。
若开环极坐标图在点(-1,j0)左方负穿越负实轴的次数 大于正穿越的次数，则闭环系统一定不稳定。
[例]如图所示系统开环极坐标图，系统开环传递函数有 2个正实部极点，闭环系统是否稳定？
Monday, June 15, 2020
在使用奈奎斯特稳定判据时，由 0 0简称为 由0 。
Monday, June 15, 2020
12
[例]开环传递函数为： G(s) ，k 用奈奎斯特
(T1s 1)(T2s 1)
稳定判据判断闭环系统的稳定性。
[解]：开环系统的奈 奎斯特图如右。在s 右半平面的极点数为 0，绕(-1,j0)点的圈 数P=0，故闭环系统 是稳定的。
20
正实部开环极点个数 P=1。由图中看出：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2014-12-22
第五章 频率响应
13
例4
K
K GH 2 ，K 0，T 0 S (1 TS )
解 : G ( j )
2 1 T 2 2
() 180 arctanT
因为 p 0， N 2 P Z， 所以 z 2 闭环系统不稳定。
F (S ) K ( S z1 )( S z 2 )( S z n ) ( S p1 )( S p 2 )( S p n )
z1， z 2， ， z n — F ( S )的零点， 也是闭环特 征方程的根 。
p1， p2， ， pn — F ( S )的极点， 也是开环 传递函数 的极点。
（2）从对数相频特性来看, G(j)平面上的负实轴,对应于对 数相频特性上的()=-180°。 （3） (-1,j0)点的向量表达式为 1∠-180°，对应于伯德图上 穿过0分贝线，并同时穿过()=-180°的点。
2014-12-22
第五章 频率响应
22
2、穿越在伯德图上的含义
（ 1 ）穿越：在 L()>0dB 的频 率范 围内 ， 相 频特 性曲线 穿 过 -180° ； 在 L()<0dB 的频 率范 围内 ， 相 频特性 曲线穿过-180°不是穿越。
2014-12-22 第五章 频率响应 18
由0变到+ 时的开环奈氏图 G(j)对(-1,j0)点的总包围次数为
N = （ N’+ - N’- ） 利用正、负穿越情况的奈奎斯 特稳定判据叙述为：
Z = P -2（ N’+ - N’- ）=0
2014-12-22
第五章 频率响应
19
[例6] 判断图示系统的闭环稳定性
N 0,逆时针旋转
2014-12-22
第五章 频率响应
7
二、奈氏稳定判据
K1 ( S z / 1 )( S z / 2 )( S z / m ) G(S ) H (S ) ( S p1 )( S p2 )( S pn )
令F (S ) 1 G(S )H (S ) 0
2014-12-22 第五章 频率响应 16
GH
K 1 (T2 ) 2
() 180 arctanT2 arctanT1
K (1 T2T1 2 ) j (T2 T1 ) G ( j ) 2 (1 (T1 ) 2 ) 2 (1 (T1 ) 2 )
（2）正穿越 N+：产生正的相 位移，相频特性应穿越180°线。 （ 3 ）负穿越 N- ：产生负的相 位移,相频特性应穿越180°线 。 正、负穿越的定义和前面的定义实际上是一致的。
2014-12-22 第五章 频率响应 23
3、对数幅频特性曲线的奈氏判据
根据上述对应关系，结合使用正、负穿越情况的稳定 判据，在伯德图上使用奈奎斯特稳定判据时，就是在L() >0dB的频率范围内，根据相频曲线穿越-180º 的相位线的次 数对系统稳定性做出判定。可将对数频率特性判断闭环系 统稳定性的奈氏稳定判据表述如下:
2014-12-22
第五章 频率响应
14
例5
解 GH K 1 (T2 ) 2
K (T2 S 1) GH 2 S (T1S 1)
分析T1和T2的相对大小对系统稳定 性的影响。
2 1 (T1 ) 2
() 180 arctanT2 arctanT1
5.3 奈奎斯特稳定判据
系统稳定的充分必要条件是系统闭环特征根都具有负实部，
即位于 s 左半平面。在时域分析中判断系统的稳定性，一种方法 是求出特征方程的全部根，另一种方法就是使用劳斯判据（代数 判据）。然而，这两种方法都有不足之处，对于高阶系统，非常 困难且费时,也不便于研究系统参数、结构对稳定性的影响。
开环频率特性曲线逆时针穿越（-∞，-1）区间时，随 ω增加，频 率特性的相角值增大，称为一次正穿越N’+。
反之，开环频率特性曲线顺时针穿越（ -∞，-1 ）区间时，随 ω增 加，频率特性的相角值减小，则称为一次负穿越N’-。 频率特性曲线包围 (-1,j0)点的情况，就可以利用频率特性曲线在 负实轴（-∞，-1）区间的正、负穿越来表达。
2014-12-22
奈氏图上的正、负穿越
伯德图上的正、负穿越
第五章 频率响应 25
例7
K G( S ) H ( S ) ，T1 T2 (T1S 1)(T2 S 1)
2( N N ) 2(0 0) z 0
z 0
闭环稳定
2014-12-22
第五章 频率响应
第五章 频率响应
11
开环传递函数在虚轴上有极点
设开环传递函数为
G(S ) H (S ) K (1 i S ) S (1 Tl S )
l 1 i 1 n m
,n m
在C2 部分上,令S e j ( 0),
(90 ,90 )
lim G( S ) H ( S ) lim s 0 0 K
必求闭环特征根；
2.能够确定系统的稳定程度（相对稳定性）； 3.可用于分析系统的瞬态性能，利于对系统的分析与设计； 4.基于系统的开环奈氏图，是一种图解法。
2014-12-22
第五章 频率响应
2
一、幅角原理
令F (S )
K ( s z1 )(s z2 ) (s zn ) ( s p1 )( s p2 ) ( s pn )
2014-12-22 第五章 频率响应 6
幅角原理：除有限个奇点外，F(s)是一个解析函数。如果S 平面上的闭合曲线Cs以顺时针方向包围F(S)的Z个零点和P
个极点，且此曲线不通过F(s)的任何极点和零点，则其在
F(s)平面上的映射曲线CF将围绕F(s)平面的坐标原点旋转N 周。
N PZ
N 0,顺时针旋转
1)T1 T2，N 0 z 0
闭环系统稳定
K (1 T2T1 2 ) j (T2 T1 ) G ( j ) 2 2 2 (1 (T1 ) ) (1 (T1 ) 2 )
2014-12-22 第五章 频率响应 15
GH
K 1 (T2 ) 2

e j
1) 1，C2 部分在GH平面上的映 射曲线为一半径无穷大 的半圆。
2014-12-22
2) 2，C2 部分在GH平面上的映 射曲线为一半径无穷大 的圆。
第五章 频率响应
12
例3
K GH ，K 0，T1 0 S (1 T1 S )
取下图所示的 奈氏途径,C2部分在GH平台上的映 射曲线为 一半径无穷大的 半圆，它与 奈氏曲线G(jω)H( jω)相连接后为 下图所示：
取S平面上封闭围线Cs为右图所示。
2014-12-22
第五章 频率响应
F ( j ) 1 G( j ) H ( j 8)
F ( j ) 1 G( j ) H ( j )
若围线Cs以顺时针方向包围了F(S)的Z个零点和P个极点，由幅 角原理可知，在F(jω)平面上的映射曲线CF将按顺时针方向围绕 坐标原点旋转N周。
2014-12-22
第五章 频率响应
21
1、奈氏图与伯德图的对应关系
开环系统幅相频率特性与对数频率特性之间存在如下对应 关系:
（1）在G(j)平面上, |G(j)|=1的单位圆,对应于对数幅频特 性的0分贝线; 单位圆外部如 (-,-1)区段，对应L () >0dB， 单位圆内部对应L () <0dB。

2
1 (T1 )
2
() 180 arctanT2 arctanT1
2)T1 T2，G( j ) H ( j )曲线穿过 (1, j 0)点， 说明闭环系统有一对虚 根， 闭环系统不稳定。
K (1 T2T1 2 ) j (T2 T1 ) G ( j ) 2 (1 (T1 ) 2 ) 2 (1 (T1 ) 2 )

2
1 (T1 )
2
3)T1 T2，N 2 z 0， 说明闭环系统有二个 闭环 极点在S平面的右方， 故闭环系统不稳定 。
2014-12-22
第五章 频率响应
17
采用穿越的概念简化复杂曲线包围次数的计算
由0变到+ 时开环频率特性曲线要
形成对(-1,j0)点的一次包围，势必穿越 （-∞，-1）区间一次。
z1， z2， ， zn — F (S )的零点
p1， p2， ， pn — F (S )的极点
2014-12-22
第五章 频率响应
3
若在S平面上任取一封闭曲线Cs,且令S以顺时针方向沿着Cs 变化,则上式求得其在F(S)平面上的映射曲线CF。
2014-12-22
第五章 频率响应
Z = P -2（ N’+ - N’- ）
由以上分析可知，开环系统型别过高会影响稳定性，而串联 比例微分调节器可以改善系统的稳定性，起到校正的作用，但要 选择合适的参数。
2014-12-22 第五章 频率响应 20
三、奈氏判据在对数坐标图上的应用
由于系统开环对数频率特性曲线的绘制较奈 奎斯特曲线更为简单、方便，自然使用伯德图来 进行系统稳定性判别就更适用。该判据不但可以 回答系统稳定与否的问题，还可以研究系统的稳 定裕量（相对稳定性），以及研究系统结构和参 数对系统稳定性的影响。
4
1）围线Cs围绕F(S)的一个零F(S)的一个零点,则其在F(S)平面上的 映射曲线CF亦按顺时针方向围绕F(S)平面的坐标原点旋转一周.
2014-12-22 第五章 频率响应 5