下载文档原格式
初一上册数学第五章知识点：一元一次方程聪明出于勤奋，天才在于积累。
尽快地掌握科学知识，迅速提高学习能力,由编辑老师为您提供的初一上册数学第五章知识点，希望给您带来启发!1.一元一次方程：只含有一个未知数，并且未知数的次数是1，并且含未知数项的系数不是零的整式方程是一元一次方程。
2.一元一次方程的标准形式：ax+b=0(x是未知数，a、b是已知数，且a0)。
3.条件：一元一次方程必须同时满足4个条件：(1)它是等式;(2)分母中不含有未知数;(3)未知数最高次项为1;(4)含未知数的项的系数不为0.4.等式的性质：等式的性质一：等式两边同时加一个数或减去同一个数或同一个整式，等式仍然成立。
等式的性质二：等式两边同时扩大或缩小相同的倍数(0除外)，等式仍然成立。
等式的性质三：等式两边同时乘方(或开方)，等式仍然成立。
解方程都是依据等式的这三个性质等式的性质一：等式两边同时加一个数或减同一个数，等式仍然成立。
5.合并同类项(1)依据：乘法分配律(2)把未知数相同且其次数也相同的相合并成一项;常数计算后合并成一项(3)合并时次数不变，只是系数相加减。
6.移项(1)含有未知数的项变号后都移到方程左边，把不含未知数的项移到右边。
(2)依据：等式的性质(3)把方程一边某项移到另一边时，一定要变号。
7.一元一次方程解法的一般步骤：使方程左右两边相等的未知数的值叫做方程的解。
一般解法：(1)去分母：在方程两边都乘以各分母的最小公倍数;(2)去括号：先去小括号，再去中括号，最后去大括号;(记住如括号外有减号的话一定要变号)(3)移项：把含有未知数的项都移到方程的一边，其他项都移到方程的另一边;移项要变号(4)合并同类项：把方程化成ax=b(a0)的形式;(5)系数化成1：在方程两边都除以未知数的系数a，得到方程的解x=b/a.8.同解方程如果两个方程的解相同，那么这两个方程叫做同解方程。
9.方程的同解原理：(1)方程的两边都加或减同一个数或同一个等式所得的方程与原方程是同解方程。
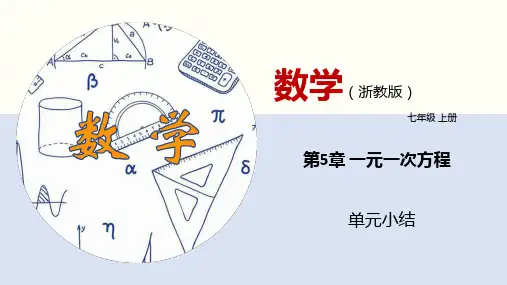
知识点总结第五章一元一次方程1、方程含有未知数的等式叫做方程。
2、方程的解能使方程左右两边相等的未知数的值叫做方程的解。
3、等式的性质（1）等式的两边同时加上（或减去）同一个代数式，所得结果仍是等式。
（2）等式的两边同时乘以同一个数（（或除以同一个不为0的数），所得结果仍是等式。
4、一元一次方程只含有一个未知数，并且未知数的最高次数是1的整式方程叫做一元一次方程。
5、移项：把方程中的某一项,改变符号后,从方程的一边移到另一边,这种变形叫做移项.6、解一元一次方程的一般步骤：（1）去分母（2）去括号（3）移项（把方程中的某一项改变符号后，从方程的一边移到另一边，这种变形叫移项。
）（4）合并同类项（5）将未知数的系数化为11、什么是一元一次方程？相信同学们都能踊跃的说出，“满足两个1即可，1个未知数且未知数指数是1的等式”，其实，在这里还要有一个前提条件：未知数的系数要不为0。
如果是0x，那就没有未知数了，就不是方程的。
2、求解一元一次的方法步骤是什么？方法：利用两条等式的性质把方程同等变形求解。
等式性质1：等式两边可以同加或同减一个代数式。
等式性质2：等式两边可以同乘或同除（除0）一个数。
步骤：（1）去分母：两边同乘分母的最小公倍数。
不能忘记还要给么有分母的项也要乘以最小公倍数。
（2）去括号：利用乘法分配率。
（3）移项：注意从等号一边跑到另一边要变号，当然，没有动的项就不要变号了。
（4）合并同类项：把同类型的系数进行相加计算。
（5）系数化为1:两边同除以系数或同乘以系数的倒数。
3、应用一元一次方程，你都记得都学习了哪些类型？（1）水箱变高了——有些题是体积，周长没变。
（2）打折销售——这些题，先要熟记公式，来，复习下售价=_________________________, 利润=____________ ,利润率=_______________然后，要根据题意看看都能表示出哪些量，最后，观察你表示出的这些量，往往等量关系就出来，方程也就出来了。
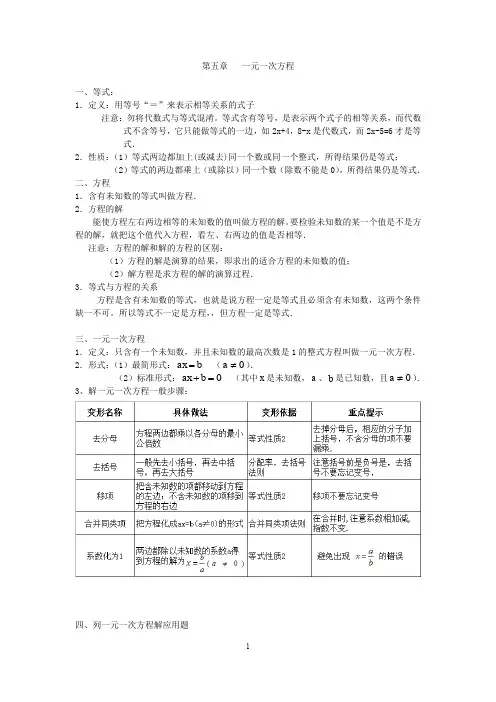
第五章 一元一次方程一、等式：1．定义：用等号“＝”来表示相等关系的式子注意：勿将代数式与等式混淆。
等式含有等号，是表示两个式子的相等关系，而代数式不含等号，它只能做等式的一边，如2x+4，8-x 是代数式，而2x-5=6才是等式．2．性质：（1）等式两边都加上(或减去)同一个数或同一个整式，所得结果仍是等式；（2）等式的两边都乘上（或除以）同一个数（除数不能是0），所得结果仍是等式．二、方程1．含有未知数的等式叫做方程．2．方程的解能使方程左右两边相等的未知数的值叫做方程的解。
要检验未知数的某一个值是不是方程的解，就把这个值代入方程，看左、右两边的值是否相等．注意：方程的解和解的方程的区别：（1）方程的解是演算的结果，即求出的适合方程的未知数的值；（2）解方程是求方程的解的演算过程．3．等式与方程的关系方程是含有未知数的等式，也就是说方程一定是等式且必须含有未知数，这两个条件缺一不可。
所以等式不一定是方程，，但方程一定是等式．三、一元一次方程1．定义：只含有一个未知数，并且未知数的最高次数是1的整式方程叫做一元一次方程．2．形式：（1）最简形式：b ax = （0≠a ）．（2）标准形式：0=+b ax （其中x 是未知数，a 、b 是已知数，且0≠a ）．3、解一元一次方程一般步骤：四、列一元一次方程解应用题1、水箱变高了——利用等积变换的思想2、打折销售商品利润= 商品售价－商品进价；利润率=商品利润÷商品进价×100%；商品售价＝标价×折扣数÷10；商品售价=商品进价×(1+利润率)。
3、“希望工程”义演工作总量＝工作时间×工作效率；工作时间＝工作总量÷工作效率；工作效率＝工作总量÷工作时间；甲的工作量＋乙的工作量＝甲乙合作的工作总量注意：工程问题常把工作总量看做“1”，解工程问题的关键是先找出单位时间内的工作效率。
第五章一元一次方程章节小结
知识点：
1、方程中的一些相关概念：
①等式：用等号连结的式子方程：含有未知数的等式
一元一次方程：方程两边是整式，含有一个未知数，未知数的指数是1
次的方程
②方程的解：使方程两边相等的未知数的值（代入方程，方程能成立）
③等式性质1：等式两边都加上或减去同一个数或式，所得结果仍是等式等式性质2：等式两边都乘以或除以同一个不为零的数或式，所得结果仍是等式
2、主要运算法则：
①解方程：化分母为整数的一般方程－去分母－去括号－移项－合并－系
审题分析－设元－列方程－解方程－检验－答
类型一：日历中的方程类型二：等积问题
类型三：调配问题
类型四：行程问题（路程速度时间）
1、路程=速度×时间
2、速度=路程÷时间
3、时间=路程÷速度
类型五：工程问题
1、工作总量 =工作效率×工作时间
2、工作效率 =工作总量÷工作时间
3、工作时间 =工作总量÷工作效率
类型六：储蓄问题
1、本息和=本金+利息
2、利息税=利息×20℅
3、利息=本金×利率×期数
应用题解题关键：找数量关系用未知数表示，找等量关系用方程表示
（关注变化过程，关注生成的等量关系）
基础知识应用
一、填空题
1、有下列式子：①434=-x ②132-=- ③5=+y x ④x x
211=+ ⑤22+=x x ⑥x 21-。
其中，属于方程的是 ；属于一元一次方程
的是 。
（填序号）
2、方程x x =-22的解是 （结果保留根号）
3、如果52=+a ，那么=+62a 。
4、如果方程02=+x 与方程22=-a x 的解相同，那么=a 。
5、某商品的进价是300元，标价是450元，现打八折销售，此时利润为 元，利润率为 。
6、小李存了年利率为2.25%的两年期存款，两年后将缴纳利息税12.15元，那么，小李存了的本金为 元，扣除利息税后从银行共可取回 元。
（利息
税为存款年产生利息的20%）
7、华氏（°F ）、摄氏（°C ）温度之间的转换公式为F=1.8C+32。
如果某天的气
温是86°F ，转换成摄氏温度，就是 °C 。
8、要加工200个零件，甲先单独加工了5小时，然后又与乙一起加工了4小时，
如果甲每小时比乙多加工2 个零件，那么甲每小时加工 个零件，乙每小
时加工 个零件。
二、选择题
1、下列说法，正确的是（ ）
A B 、方程是代数式 C 、等式是方程 D 、方程是等式
2、设“
如果要使第三架天平也平衡，那么“?”处应放“ ”的个数为（ ）
A 、3
B 、4
C 、5
D 、6
3、方程
352
=-x 的解与下列哪个方程的解相同？答：（ ） A 、43=x B 、83=x C 、133=x D 、163=x
4、方程43
4=--x x 的解题步骤如下，错误开始于（ ） A 、1243=--x x B 、4123+=-x x C 、162=x D 、8=x
5、在梯形面积公式h b a s )(2
1+=中，如果16=s ，3=a ，4=h ，那么b 的值为（ ）A 、4 B 、5 C 、6 D 、7 6、一个圆柱形容器盛有
54容积的酒精，从中倒出20升后，容器中的酒精还占这个容器的3
2容积，那么这个容器的容积是（ ）。
A 、150升 B 、120升 C 、100升 D 、90升
7、用直径为40mm 的圆钢，锻造一个直径为200mm ，厚为18mm 的圆柱形毛坏，不计损耗，应截取圆钢的长为（ ）
A 、350mm
B 、400mm
C 、450mm
D 、500mm
8、在一次美化校园的活动中，老师安排32人除草，18人植树。
后来发现人手不够，就增派20人去支援，并且使除草的人数是植树人数的2倍。
问：增派的20人中，支援除草的有多少人？设支援除草的有x 人，下列方程中正确的是（ ）
A 、18232⨯=+x
B 、)38(232x x -=+
C 、)18(252x x +=-
D 、18252⨯=-x
三、解答题（共46分）
1、解下列方程：
（1）6734-=+x x （2）331=+-
x x
（3）
142312-+=-y y （4）17.03.027.1-=-x x
2、如果1=x 是方程2
1321-=x mx 的解，求代数式20052)97(+-m m 的值。
四、方程应用
1、2004年衢州市农业生产呈良好的发展态势，粮食生产出现转机，农民种粮积极性提高，粮食总产量为85万吨，比上年增长16.7%。
问：2003年衢州市粮食总产量为多少万吨？（精确到0.1万吨）
2、一份稿件，甲打字员单独打20天可以完成，乙打字员单独打30天可以完成。
现由两人合打8天后，余下部分由乙单独打，还需多少天完成？
3、在100名学生中，会打乒乓球的有83人，会打排球的有75人，这两项都不会的有10人，问这两项都会的有多少人？
4、小林每时走5千米，小洪每时走4千米，两人同时从A 村出发去B 村，出发0.5小时后，小林因事返回A 村，在A 村停留15分钟后再去B 村，这样与小洪同时到达B 村，求A 、B 两村的距离。
四、能力拓展题（附加题20分）
1、（1）如果单项式3132
1b a m -与n b a 54-是同类项，求m 、n 的值。
（2）如果关于x 的方程b x ax +=-133有无数多个解，求a 、b 的值。
2、一项工程，由甲队独做需12个月完工，由乙队独做需15个月完工. 现决定由两队合作，且为了加快进度，甲、乙两队都将提高工作效率. 若甲队的工作效率提高40%，乙队的工作效率提高25%，则两队合作，几个月可以完工？
3、有一个允许单向通过的窄道口，通常情况下，每分钟可以通过9人，一天，王老师到达道口时，发现由于拥挤，每分钟只能3人通过道口，此时，自己前面还有36人等待通过（假定先到先过，王老师过道口的时间忽略不计），通过道口后，还需7分钟到达学校。
（1） 此时，若绕道而行，要15分种到达学校，从节省时间考虑，王老师应选择
绕道去学校，还是选择通过拥挤的道口去学校？
（2） 若在王老师等人的维持下，几分钟后，秩序恢复正常（维持秩序期间，每分
钟仍有3人通过道口），结果王老师比拥挤情况下提前了6分钟通过道口，问维持秩序的时间是多少？。
