常见定位方式定位误差的计算

定位误差的分析与计算一、定位误差的概念和原因定位误差是指定位系统测量结果与真实位置之间的差异或偏差。

在现代生活中，定位系统广泛应用于导航系统、无人驾驶、无人飞行器等领域，而定位误差对于系统的准确性和可靠性至关重要。

1.信号传播误差：这是由于信号在传播过程中受到大气中的影响，如电离层、大气湿度等所产生的误差。

这种误差对于GPS系统尤为明显，导致多径效应、钟差误差等。

2.接收机误差：接收机的硬件和软件系统可能存在不同程度的误差。

硬件方面，接收机的时钟精度、天线阻抗匹配等问题都可能导致定位误差。

软件方面，接收机的算法、数据处理等也可能引入误差。

3.观测误差：观测误差是指由于测量设备的精度或不完善性所导致的误差。

例如，测量设备的精度限制了对信号强度、TOA（Time of Arrival）等参数的准确测量。

4.环境因素：环境因素也是定位误差产生的原因之一、比如，建筑物、树木、走廊等物体会对信号传播产生阻碍和衍射，从而影响接收机的测量结果。

5.多径效应：多径效应是指信号传播过程中，信号除了直射到达接收机外，还经历了反射，导致信号的多个传播路径同时到达接收机。

多径效应会产生明显的信号干扰和测量误差。

二、定位误差的计算方法1.位置误差计算：位置误差是指实际测量位置与真实位置之间的距离差异。

一种常见的计算方法是通过比较GPS测量点与参考点之间的差异来计算位置误差。

通过收集多个测量点的数据，可以使用最小二乘法进行曲线拟合，从而计算出测量点与真实位置之间的距离差异。

2.时间误差计算：时间误差是指实际测量时间与真实时间之间的差异。

在GPS系统中，时间误差主要由于卫星钟的钟差所引起。

通过GPS接收机接收到的卫星信号的时间戳和GPS接收机内部的时间戳之间的差异，可以计算出时间误差。

4.误差修正算法：为了减小定位误差，可以使用一些误差修正算法来对测量结果进行修正。

一种常见的方法是差分GPS技术，通过使用两个或多个接收机接收同一卫星信号，对测量结果进行差分处理，从而减小定位误差。

（3）定位误差的计算由于定位误差ΔD是由基准不重合误差和基准位移误差组合而成的，因此在计算定位误差时，先分别算出Δ B和ΔY ，然后将两者组合而得ΔD。

组合时可有如下情况。

1)Δ Y ≠ 0，Δ B=O时Δ D= Δ B (4.8)2)ΔY =O，Δ B ≠ O时Δ D= Δ Y (4.9)3)Δ Y ≠ 0, Δ B ≠ O时如果工序基准不在定位基面上Δ D=Δ y + Δ B (4.10)如果工序基准在定位基面上Δ D=Δ y ±Δ B (4.11)“ + ” ，“—” 的判别方法为:①设定位基准是理想状态，当定位基面上尺寸由最大实体尺寸变为最小实体尺寸 (或由小变大)时，判断工序基准相对于定位基准的变动方向。

②② 设工序基准是理想状态，当定位基面上尺寸由最大实体尺寸变为最小实体尺寸 (或由小变大)时，判断定位基准相对其规定位置的变动方向。

③③ 若两者变动方向相同即取“ + ” ，两者变动方向相反即取“—”。

－、定位误差及其组成图9-21a图9-21 工件在V 形块上的定位误差分析工序基准和定位基准不重合而引起的基准不重合误差，以表示由于定位基准和定位元件本身的制造不准确而引起的定位基准位移误差，以表示。

定位误差是这两部分的矢量和。

二、定位误差分析计算（一）工件以外圆在v形块上定位时定位误差计算如图9-16a所示的铣键槽工序，工件在v 形块上定位，定位基准为圆柱轴心线。

如果忽略v形块的制造误差，则定位基准在垂直方向上的基准位移误差（9-3）对于9-16中的三种尺寸标注，下面分别计算其定位误差。

当尺寸标注为B1时，工序基准和定位基准重合，故基准不重合误差ΔB=0。

所以B1尺寸的定位误差为（9-4）当尺寸标注为B2时，工序基准为上母线。

此时存在基准不重合误差所以△D应为△B与Δy的矢量和。

由于当工件轴径由最大变到最小时，和Δy都是向下变化的，所以，它们的矢量和应是相加。

故（9-5）当尺寸标注为B3时，工序基准为下母线。

机械加工定位误差分析（上）如前所述，为保证工件的加工精度，工件加工前必须正确的定位。

所谓正确的定位，除应限制必要的自由度、正确地选择定位基准和定位元件之外，还应使选择的定位方式所产生的误差在工件允许的误差范围以内。

本节即是定量地分析计算定位方式所产生的定位误差，以确定所选择的定位方式是否合理。

使用夹具时造成工件加工误差的因素包括如下四个方面：（ 1）与工件在夹具上定位有关的误差，称为定位误差 D ；（ 2）与夹具在机床上安装有关的误差，称为安装误差 A ；（ 3）与刀具同夹具定位元件有关的误差，称为调整误差T ；（ 4 ）与加工过程有关的误差，称为过程误差 G 。

其中包括机床和刀具误差、变形误差和测量误差等。

为了保证工件的加工要求，上述误差合成后不应超出工件的加工公差δK，即D + A +T +G ≤δ K本节先分析与工件在夹具中定位有关的误差，即定位误差有关的内容。

由定位引起的同一批工件的设计基准在加工尺寸方向上的最大变动量，称为定位误差。

当定位误差 D ≤ 1/3δ K，一般认为选定的定位方式可行。

一、定位误差产生的原因及计算造成定位误差的原因有两个：一个是由于定位基准与设计基准不重合，称为基准不重合误差（基准不符误差）；二是由于定位副制造误差而引起定位基准的位移，称为基准位移误差。

（一）基准不重合误差及计算由于定位基准与设计基准不重合而造成的定位误差称为基准不重合误差，以 B 来表示。

图 3 -61a 所示为零件简图，在工件上铣缺口，加工尺寸为 A 、B 。

图 3-61b 为加工示意图，工件以底面和E 面定位， C 为确定刀具与夹具相互位置的对刀尺寸，在一批工件的加工过程中C 的位置是不变的。

加工尺寸 A的设计基准是 F ，定位基准是 E ，两者不重合。

当一批工件逐个在夹具上定位时，受尺寸S±δ S /2的影响，工序基准 F 的位置是变动的， F 的变动影响 A 的大小，给 A 造成误差，这个误差就是基准不重合误差。

基准位移误差及计算由于定位副的制造误差而造成定位基准位置的变动，对工件加工尺寸造成的误差 , 称为基准位移误差，用Δ Y 来表示。

显然不同的定位方式和不同的定位副结构，其定位基准的移动量的计算方法是不同的。

下面，分析几种常见的定位方式产生的基准位移误差的计算方法：1 ．工件以平面定位工件以平面定位时的基准位移误差计算较方便。

如图 3-61 所示的工件以平面定位时，定位基面的位置可以看成是不变动的，因此基准位移误差为零，即工件以平面定位时Δ Y =02 ．工件以圆孔在圆柱销、圆柱心轴上定位工件以圆孔在圆柱销、圆柱心轴上定位、其定位基准为孔的中心线，定位基面为内孔表面。

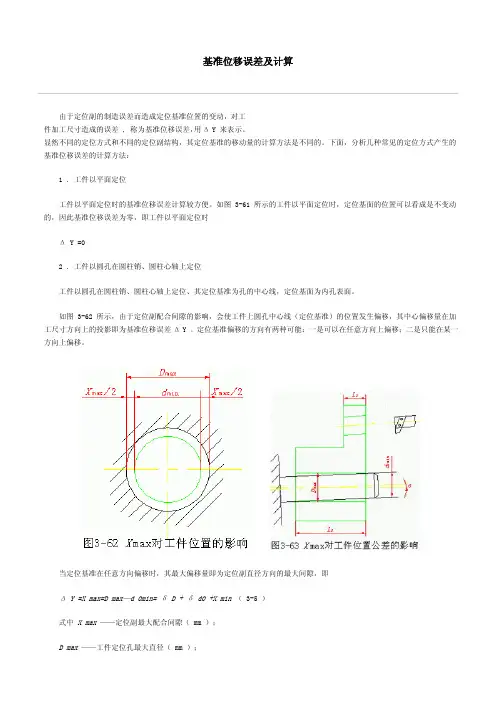
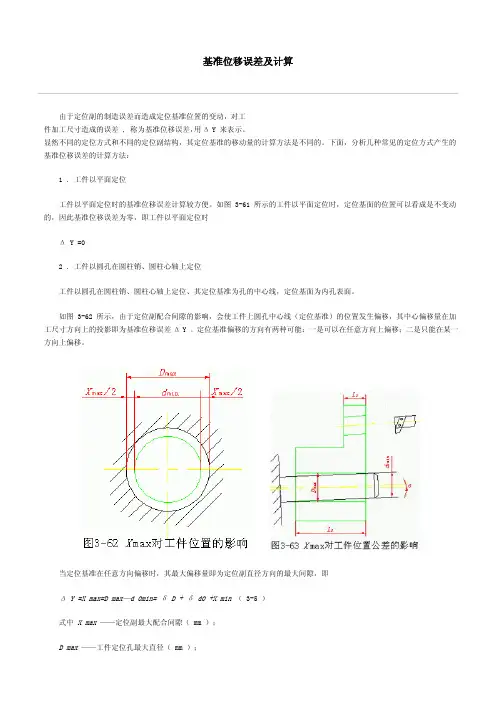
如图 3-62 所示，由于定位副配合间隙的影响，会使工件上圆孔中心线（定位基准）的位置发生偏移，其中心偏移量在加工尺寸方向上的投影即为基准位移误差Δ Y 。

定位基准偏移的方向有两种可能：一是可以在任意方向上偏移；二是只能在某一方向上偏移。

当定位基准在任意方向偏移时，其最大偏移量即为定位副直径方向的最大间隙，即 Δ Y =X max=D max—d 0min= δ D + δ d0 +X min （ 3-5 ）式中 X max ——定位副最大配合间隙（ mm ）；D max ——工件定位孔最大直径（ mm ）；d 0min ——圆柱销或圆柱心轴的最小直径（ mm ）；δ D ——工件定位孔的直径公差（ mm ）；δ d0 ——圆柱销或圆柱心轴的直径公差（ mm ）；X min ——定位所需最小间隙，由设计时确定（ mm ）。

当基准偏移为单方向时，在其移动方向最大偏移量为半径方向的最大间隙，即Δ Y = （ 1/2 ） X max= （ 1/2 ）（ D max-d 0min ） = （ 1/2 ）（δ D + δ d +X min ） （ 3-6 ）如果基准偏移的方向与工件加工尺寸的方向不一致时，应将基准的偏移量向加工尺寸方向上投影，投影后的值才是此加工尺寸的基准位移误差。

基准位移误差及计算由于定位副的制造误差而造成定位基准位置的变动，对工件加工尺寸造成的误差 , 称为基准位移误差，用Δ Y 来表示。

显然不同的定位方式和不同的定位副结构，其定位基准的移动量的计算方法是不同的。

下面，分析几种常见的定位方式产生的基准位移误差的计算方法：1 ．工件以平面定位工件以平面定位时的基准位移误差计算较方便。

如图 3-61 所示的工件以平面定位时，定位基面的位置可以看成是不变动的，因此基准位移误差为零，即工件以平面定位时Δ Y =02 ．工件以圆孔在圆柱销、圆柱心轴上定位工件以圆孔在圆柱销、圆柱心轴上定位、其定位基准为孔的中心线，定位基面为内孔表面。

如图 3-62 所示，由于定位副配合间隙的影响，会使工件上圆孔中心线（定位基准）的位置发生偏移，其中心偏移量在加工尺寸方向上的投影即为基准位移误差Δ Y 。

定位基准偏移的方向有两种可能：一是可以在任意方向上偏移；二是只能在某一方向上偏移。

当定位基准在任意方向偏移时，其最大偏移量即为定位副直径方向的最大间隙，即 Δ Y =X max=D max—d 0min= δ D + δ d0 +X min （ 3-5 ）式中 X max ——定位副最大配合间隙（ mm ）；D max ——工件定位孔最大直径（ mm ）；d 0min ——圆柱销或圆柱心轴的最小直径（ mm ）；δ D ——工件定位孔的直径公差（ mm ）；δ d0 ——圆柱销或圆柱心轴的直径公差（ mm ）；X min ——定位所需最小间隙，由设计时确定（ mm ）。

当基准偏移为单方向时，在其移动方向最大偏移量为半径方向的最大间隙，即Δ Y = （ 1/2 ） X max= （ 1/2 ）（ D max-d 0min ） = （ 1/2 ）（δ D + δ d +X min ） （ 3-6 ）如果基准偏移的方向与工件加工尺寸的方向不一致时，应将基准的偏移量向加工尺寸方向上投影，投影后的值才是此加工尺寸的基准位移误差。

定位误差的计算方法：（1）合成法为基准不重合误差和基准位移误差之和； （2）极限位置法工序基准相对于刀具（机床）的两个极限位置间的距离就是定位误差； （3）微分法先用几何方法找出工序基准到定位元件上某一固定点的距离，然后对其全微分，用微小增量代替微分，将尺寸误差视为微小增量代入，就可以得到某一加工尺寸的定位误差。

注：基准不重合误差和基准位移误差它们在工序尺寸方向上的投影之和即为定位误差。

例如：用V 型块定位铣键槽，键槽尺寸标注是轴的中心到键槽底面的尺寸H 。

T D 为工件定位外圆的公差；α为V 型块夹角。

1. 工序基准为圆柱体的中心线。

表示一批工件依次放到V 型块上定位时所处的两个极端位置情形，当工件外圆直径尺寸为极大和极小时，其工件外圆中心线分别出于点O '和点O ''。

因此工序基准的最大位置变动量O O '''，便是对加工尺寸H 1所产生的定位误差： 故得：OE O E H H O O 11DH1''-'='-''='''=ε O A E Rt 1''∆中： max 1D 21A O ='' 2sin A O O E 1α''='O A E Rt 1''''∆中：min 1D 21A O ='''' 2sin A O O E 1α''''=''2sin 2T 2sin 2T 2sin A O A O O E O E D D11DH1α=α=α''''-''=''-'=ε2. 工序基准为圆柱体的下母线：工件加工表面以下母线C 为其工序基准时，工序基准的极限位置变动量C C '''就是加工尺寸H2所产生的定位误差。

定位误差计算方法定位误差是指实际测量值与真实值之间的差异，用于衡量一个位置测量结果的准确性。

在现代定位技术中，定位误差是一个关键指标，其精度直接影响定位系统的可靠性和有效性。

本文将介绍几种常见的定位误差计算方法。

一、绝对误差绝对误差是指实际测量值与真实值之间的差异，通常以绝对值表示。

绝对误差可以直观地描述一个定位系统的精度，但不适用于不同测量结果之间的比较。

二、平均误差平均误差是指多次测量结果的平均值与真实值之间的差异。

平均误差可以通过下式计算：平均误差=Σ(测量值-真实值)/测量次数平均误差可以用来衡量一个定位系统的整体准确性，但不能反映观测数据的离散程度。

三、均方根误差均方根误差是指实际测量值与真实值之间的差异的平方的平均值的平方根，通常用RMSE表示。

均方根误差是一种常用的测量指标，可以综合考虑测量结果的离散程度和偏差。

均方根误差可以通过下式计算：RMSE = sqrt(Σ(测量值 - 真实值)² / 测量次数)均方根误差越小，定位系统的精度越高。

四、标准差标准差是一种常见的测量结果离散程度的度量方法，它表示一组测量结果相对于均值的分散程度。

标准差可以通过下式计算：标准差= sqrt(Σ(测量值 - 均值)² / 测量次数)标准差越小，定位系统的精度越高。

五、置信椭圆置信椭圆是一种用于描述定位误差的图形表示方式，能够直观地展示定位系统的误差分布情况。

置信椭圆的形状和大小可以通过计算定位误差的均值和方差来确定。

通常情况下，置信椭圆的中心为测量结果的平均值，长轴和短轴的长度与测量结果的方差相关。

六、相关误差相关误差是指多个测量结果之间的相关性误差。

相关误差可以通过计算测量结果之间的协方差来确定。

相关误差可以反映定位系统中不同观测量之间的相互影响程度。

综上所述，定位误差计算方法多种多样，常见的包括绝对误差、平均误差、均方根误差、标准差和置信椭圆等。

不同的误差计算方法适用于不同的情况，可以综合使用来评估一个定位系统的准确性和可靠性。

常见定位方式定位误差的计算定位误差是指实际定位结果与真实位置之间的偏差。

常见的定位方式包括全球定位系统（GPS）、移动通信系统（如基站定位）、无线传感器网络、惯性测量单元等。

下面我将对其中几种常见的定位方式的定位误差计算进行介绍。

1.GPS定位误差计算：GPS是一种基于卫星信号的定位系统，它通过接收来自卫星的信号来测量和计算位置。

GPS定位误差的计算主要涉及到以下几个方面：-接收机定位误差：GPS接收机的性能和质量也会影响定位的精度。

定位误差可以通过接收机的接收灵敏度、信噪比和多路径效应等因素来计算。

-卫星时钟误差：GPS中的卫星时钟误差会对定位结果产生影响。

在定位的过程中，需要校正卫星的时钟误差，以提高定位的精度。

-接收机钟差：GPS接收机的内部时钟精度也会对定位结果产生影响。

为了减小时钟误差带来的影响，可以采用差分GPS的方法来校正时钟误差。

-多路径效应：在GPS信号的传输过程中，会经历多次反射和散射，导致接收机接收到多个不同路径上的信号。

这些多路径效应会对定位结果产生误差。

可以通过衡量同一卫星的信号在空间中的多路径效应来计算定位误差。

2.基站定位误差计算：基站定位是一种利用移动通信系统中的基站设备对移动终端进行定位的方式。

基站定位误差的计算主要涉及到以下几个方面：-平均距离误差（RTK错误）：基站定位中常常使用差分定位技术，通过测量基站与移动终端之间的距离差，来对移动终端的位置进行计算。

平均距离误差是指多次测量的距离平均误差，可以通过对多组测量数据进行统计来计算。

3.无线传感器网络定位误差计算：无线传感器网络是由分布式传感节点组成的网络系统，用于采集和传输环境信息。

无线传感器网络定位误差的计算主要涉及到以下几个方面：-距离估计误差：无线传感器网络中的节点之间通常通过测量信号强度来估计节点之间的距离。

距离估计误差是指估计值与真实值之间的偏差，可以通过多组测量数据的均值和方差来计算。

-锚定节点误差：无线传感器网络中通常会设置一些已知位置的锚定节点，用于提供参考位置。

定位误差分析计算 1、工件以平面定位（1）如图所示工件图样，底面已经加工完成，以工件底面定位铣加工台阶面，保证尺寸20±0.15，其定位误差是多少？该种定位方法是否满足工序的要求？工序分析工序内容：铣平面工序要求：20±0.15（T=0.3） 工序基准：顶面 定位基准：底面基准不重合误差：△B=0.14×2=0.28(两基准间尺寸公差在加工尺寸方向上的投影) 基准位移误差：△W=0(精基准平面定位，基准位移误差可以不考虑) 定位误差：△D=△B+△W=0.28（工序基准不在定位基面上△D=△B+△W ）定位质量评定：△D=0.28＞（T/3=0.1） 不满足工序要求 解决办法：（1）定位方案不变，提高定位尺寸的精度，以减少△D 的数值；（2）改变定位方案。

（2）如图所示箱体类工件图样，底面和中间通孔已经加工完成，以工件底面定位铣加工平面，保证尺寸28±0.1，其定位误差是多少？该种定位方法是否满足工序的要求？工序分析工序内容：铣平面工序要求：28±0.1（T=0.2） 工序基准：孔轴线 定位基准：底面基准不重合误差：△B=0.1×2×cos45°=0.1414 (两基准间尺寸公差在加工尺寸方向上的投影) 基准位移误差：△W=0(精基准平面定位，基准位移误差可以不考虑) 定位误差：△D=△B+△W=0.1414（工序基准不在定位基面上△D=△B+△W ）定位质量评定：△D=0.1414＞（T/3=0.0667） 不满足工序要求 解决办法：（1）定位方案不变，提高定位尺寸的精度，以减少△D 的数值；（2）改变定位方案。

（3）下图所示工件，A 、B 面已由前道工序加工完成。

本铣槽工序要求确保尺寸50±0.05mm ，宽度30±0.042mm 由铣刀尺寸保证，试检验本方案的定位精度是否满足加工要求。

若不能满足加工要求，可采用什么方案定位？工序分析工序内容：铣槽工序要求：50±0.05mm (T=0.1mm) 工序基准：B 面 定位基准：左端面 基准不重合误差：△B=0.065×2+0.055×2=0.24mm (两基准间尺寸公差在加工尺寸方向上的投影) 基准位移误差：△W=0(精基准平面定位，基准位移误差可以不考虑) 定位误差：△D=△B+△W=0.24mm（工序基准不在定位基面上△D=△B+△W ）定位质量评定：△D=0.24＞（T/3=0.033） 不满足工序要求（4）如下图所示，工件镗孔加工图样，孔1和孔2均已加工完成，以工件底面A 为基准镗削孔3，要求保证尺寸（15±0.055）mm ，试检验f 该方案的定位精度。