非线性模型参数估计方法步骤
- 格式:doc
- 大小:49.50 KB
- 文档页数:2



非线性回归分析的入门知识在统计学和机器学习领域,回归分析是一种重要的数据分析方法,用于研究自变量和因变量之间的关系。
在实际问题中,很多情况下自变量和因变量之间的关系并不是简单的线性关系,而是呈现出一种复杂的非线性关系。
因此,非线性回归分析就应运而生,用于描述和预测这种非线性关系。
本文将介绍非线性回归分析的入门知识,包括非线性回归模型的基本概念、常见的非线性回归模型以及参数估计方法等内容。
一、非线性回归模型的基本概念在回归分析中,线性回归模型是最简单和最常用的模型之一,其数学表达式为:$$Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + ... + \beta_pX_p +\varepsilon$$其中,$Y$表示因变量,$X_1, X_2, ..., X_p$表示自变量,$\beta_0, \beta_1, \beta_2, ..., \beta_p$表示模型的参数,$\varepsilon$表示误差项。
线性回归模型的关键特点是因变量$Y$与自变量$X$之间呈线性关系。
而非线性回归模型则允许因变量$Y$与自变量$X$之间呈现非线性关系,其数学表达式可以是各种形式的非线性函数,例如指数函数、对数函数、多项式函数等。
一般来说,非线性回归模型可以表示为:$$Y = f(X, \beta) + \varepsilon$$其中,$f(X, \beta)$表示非线性函数,$\beta$表示模型的参数。
非线性回归模型的关键在于确定合适的非线性函数形式$f(X,\beta)$以及估计参数$\beta$。
二、常见的非线性回归模型1. 多项式回归模型多项式回归模型是一种简单且常见的非线性回归模型,其形式为: $$Y = \beta_0 + \beta_1X + \beta_2X^2 + ... + \beta_nX^n +\varepsilon$$其中,$X^2, X^3, ..., X^n$表示自变量$X$的高次项,$\beta_0, \beta_1, \beta_2, ..., \beta_n$表示模型的参数。
(整理)计量经济学第四章⾮线性回归模型的线性化第四章⾮线性回归模型的线性化以上介绍了线性回归模型。
但有时候变量之间的关系是⾮线性的。
例如 y t = α 0 + α11βt x + u t y t = α 0 t x e 1α+ u t上述⾮线性回归模型是⽆法⽤最⼩⼆乘法估计参数的。
可采⽤⾮线性⽅法进⾏估计。
估计过程⾮常复杂和困难,在20世纪40年代之前⼏乎不可能实现。
计算机的出现⼤⼤⽅便了⾮线性回归模型的估计。
专⽤软件使这种计算变得⾮常容易。
但本章不是介绍这类模型的估计。
另外还有⼀类⾮线性回归模型。
其形式是⾮线性的,但可以通过适当的变换,转化为线性模型,然后利⽤线性回归模型的估计与检验⽅法进⾏处理。
称此类模型为可线性化的⾮线性模型。
下⾯介绍⼏种典型的可以线性化的⾮线性模型。
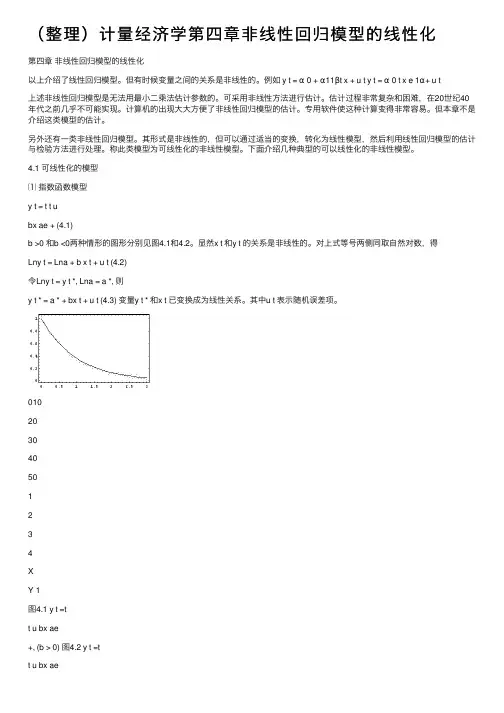
4.1 可线性化的模型⑴指数函数模型y t = t t ubx ae + (4.1)b >0 和b <0两种情形的图形分别见图4.1和4.2。
显然x t 和y t 的关系是⾮线性的。
对上式等号两侧同取⾃然对数,得Lny t = Lna + b x t + u t (4.2)令Lny t = y t *, Lna = a *, 则y t * = a * + bx t + u t (4.3) 变量y t * 和x t 已变换成为线性关系。
其中u t 表⽰随机误差项。
010203040501234XY 1图4.1 y t =tt u bx ae+, (b > 0) 图4.2 y t =t+, (b < 0)⑵对数函数模型y t = a + b Ln x t+ u t(4.4)b>0和b<0两种情形的图形分别见图4.3和4.4。
x t和y t的关系是⾮线性的。
令x t* = Lnx t, 则y t = a + b x t* + u t(4.5)变量y t和x t* 已变换成为线性关系。
图4.3 y t = a + b Lnx t + u t , (b > 0) 图4.4 y t = a + b Lnx t + u t , (b < 0)⑶幂函数模型y t= a x t b t u e(4.6) b取不同值的图形分别见图4.5和4.6。

非线性回归模型的拟合与评估非线性回归是统计学中常用的一种回归分析方法,用于描述自变量与因变量之间的非线性关系。
本文将介绍非线性回归模型的拟合与评估方法。
一、非线性回归模型的拟合方法1. 数据收集与准备拟合非线性回归模型首先需要收集与问题相关的数据。
数据的准备包括数据清洗、变量选择和数据变换等步骤,以确保数据的质量和适应非线性回归模型的要求。
2. 模型选择在准备好数据后,需要选择适合问题的非线性回归模型。
常见的非线性回归模型包括多项式回归模型、指数回归模型、对数回归模型等。
选择合适的模型需要根据问题的特点和理论的支持进行判断。
3. 模型拟合模型拟合是指通过最小化残差平方和或最大似然估计等方法,估计模型的参数。
对于非线性回归模型,常用的拟合方法有最小二乘法、非线性最小二乘法、广义最小二乘法等。
4. 拟合效果评估拟合效果评估是判断非线性回归模型拟合程度好坏的指标。
常用的评估方法有残差分析、决定系数、AIC和BIC等。
残差分析可以检验模型的拟合效果和残差的独立性、常数方差和正态性假设。
二、非线性回归模型的评估方法1. 决定系数(R-squared)决定系数是衡量模型拟合程度的指标,其取值范围为0到1之间。
决定系数越接近1,表示模型对观测数据的解释能力越强。
但需要注意,决定系数无法判断模型是否过拟合。
2. 调整决定系数(Adjusted R-squared)调整决定系数是对决定系数进行修正,考虑了自变量数目的影响。
调整决定系数比决定系数更能有效地评估模型的拟合效果。
3. Akaike信息准则(AIC)和贝叶斯信息准则(BIC)AIC和BIC是用于比较不同模型的拟合效果的统计准则。
AIC和BIC数值越小,表示模型越好。
这两个指标在非线性回归模型的选择和评估中广泛应用。
4. 拟合图形分析通过绘制拟合曲线与实际观测数据的对比图,可以直观地评估非线性回归模型的拟合效果。
拟合图形分析可以帮助发现模型的不足之处,从而进行进一步的改进。

EViews非线性模型参数估计方法步骤1.新建EViews工作区,并将时间序列X、P1和P0导入到工作区;2.设定参数的初始值全部为1,其方法是在工作区中其输入下列命令并按回车键param c(1) 1 c(2) 1 c(3) 1 c(4) 13.估计非线性模型参数,其方法是在工作区中其输入下列命令并按回车键nls q=exp(c(1))*x^c(2)*p1^c(3)*p0^c(4)4.得到结果见table01(91页表3.5.4结果)(案例一结束)Dependent Variable: QMethod: Least SquaresDate: 03/29/15 Time: 21:44Sample: 1985 2006Included observations: 22Convergence achieved after 9 iterationsQ=EXP(C(1))*X^C(2)*P1^C(3)*P0^C(4)Coefficient Std. Error t-Statistic Prob.C(1) 5.567708 0.083537 66.64931 0.0000C(2) 0.555715 0.029067 19.11874 0.0000C(3) -0.190154 0.143823 -1.322146 0.2027C(4) -0.394861 0.159291 -2.478866 0.0233R-squared 0.983631 Mean dependent var 1830.000Adjusted R-squared 0.980903 S.D. dependent var 365.1392S.E. of regression 50.45954 Akaike info criterion 10.84319Sum squared resid 45830.98 Schwarz criterion 11.04156Log likelihood -115.2751 Hannan-Quinn criter. 10.88992Durbin-Watson stat 0.672163(92页表3.5.5结果)(案例二过程)5.新建EViews工作区,并将时间序列X、P1和P0导入到工作区;6.设定参数的初始值全部为1,其方法是在工作区中其输入下列命令并按回车键param c(1) 1 c(2) 1 c(3) 17.估计非线性模型参数,其方法是在工作区中其输入下列命令并按回车键nls q=exp(c(1))*(x/p0)^c(2)*(p1/p0)^c(3)8.得到结果见table02(92页表3.5.5结果)(案例二结束)Dependent Variable: QMethod: Least SquaresDate: 03/29/15 Time: 22:14Sample: 1985 2006Included observations: 22Convergence achieved after 4 iterationsQ=EXP(C(1))*(X/P0)^C(2)*(P1/P0)^C(3)Coefficient Std. Error t-Statistic Prob.C(1) 5.525965 0.072685 76.02666 0.0000C(2) 0.533824 0.019785 26.98163 0.0000C(3) -0.242862 0.134014 -1.812219 0.0858R-squared 0.982669 Mean dependent var 1830.000Adjusted R-squared 0.980845 S.D. dependent var 365.1392S.E. of regression 50.53638 Akaike info criterion 10.80939Sum squared resid 48524.59 Schwarz criterion 10.95817Log likelihood -115.9033 Hannan-Quinn criter. 10.84444Durbin-Watson stat 0.656740。

参数估计的一般步骤
参数估计是统计学中的一种方法,用于根据样本数据估计总体参数的值。
它是一个重要的统计推断技术,可以帮助我们了解和描述总体的特征。
参数估计的一般步骤如下:
1. 确定研究对象和目标参数:首先,我们需要明确研究对象是什么,需要估计的是哪个参数。
例如,我们可能希望估计某个产品的平均寿命,那么研究对象是产品,目标参数是平均寿命。
2. 收集样本数据:为了进行参数估计,我们需要收集一定数量的样本数据。
样本应该能够代表总体,并且必须是随机选择的,以避免抽样偏差。
3. 选择合适的估计方法:根据研究对象和目标参数的不同,我们可以选择不同的估计方法。
常见的估计方法包括点估计和区间估计。
点估计给出一个单一的数值作为参数的估计值,而区间估计给出一个范围,以表明参数估计值的不确定性。
4. 计算估计值:根据选择的估计方法,我们可以使用样本数据计算出参数的估计值。
例如,对于平均寿命的估计,我们可以计算样本的平均值作为总体平均寿命的估计值。
5. 评估估计的准确性:估计值的准确性可以通过计算估计的标准误
差或置信区间来评估。
标准误差反映了估计值与真实参数值之间的差异,而置信区间提供了参数估计值的不确定性范围。
6. 解释和应用估计结果:最后,我们需要解释估计结果并应用于实际问题中。
根据估计结果,我们可以得出结论,做出决策或提出建议。
参数估计是一种重要的统计推断方法,可以帮助我们了解总体特征并做出准确的推断。
通过正确的步骤和方法,我们可以获得可靠的参数估计结果,并将其应用于实际问题中。

非线性系统模型参数估计的算法模型摘要:针对非线性系统模型的多样性,提出了适用于多种非线性模型的基于粒子群优化算法的参数估计方法。
计算结果表明,粒子群优化算法是非线性系统模型参数估计的有效工具。
关键词:粒子群优化算法;非线性系统;参数估计;优化abstract: aiming at the diversity of nonlinear system model, it is proposed in this article a parameter estimation method based on particle group optimization algorithm that is applicable to a variety of nonlinear models. the result shows that the particle group optimization algorithm for parameter estimation of nonlinear system model is an effective tool. key words: particle group optimization algorithm;nonlinear system; parameter estimation; optimization0 引言非线性系统广泛地存在于人们的生产生活中,但是,目前我们对非线性系统的认识还不够深入,不能像线性系统那样,把所涉及的模型全部规范化,从而使辩识方法也规范化。
非线性模型的表达方式相对比较复杂,目前还很少有人研究各种表达方式是否存在等效关系,因此,暂时还没有找到对所有非线性模型都适用的参数模型估计方法[1]。
如果能找到一种不依赖于非线性模型的表达方式的参数估计方法,那么,也就找到了对一般非线性模型系统进行参数估计的方法[2]。
粒子群优化算法[3](particle swarm optimaziton,简称pso)是由kennedy博士和eberhart博士于1995年提出的一种基于群体智能的优化算法,它源于对鸟群群体运动行为的研究,即粒子群优化算法模拟鸟群的捕食行为。


非线性成长模型的建立与参数估计非线性成长模型是一种用来描述非线性系统的变化过程的数学模型。
相比于线性模型,非线性成长模型可以更准确地反映实际问题中的非线性关系,因此在很多领域应用广泛,比如生物学、经济学和环境科学等。
在本篇文章中,我们将探讨如何建立非线性成长模型并进行参数估计的方法与步骤。
首先,建立非线性成长模型需要明确研究对象的特征以及模型的形式。
我们以生物学中的生长过程为例。
假设我们想要研究一种植物的生长过程,并希望建立一个非线性成长模型来描述其生长速度随时间的变化。
根据观察,我们发现该植物的生长速度在初始阶段比较快,逐渐减缓,最终接近一个稳定值。
基于这一观察,我们可以选择广义 logistic 函数作为非线性成长模型的形式:N(N) = N / (1 + N^−N(N−N₀))其中N(N)表示植物的生长速度,N表示最大生长速度,N表示生长速度的增长率,N₀表示生长速度达到一半最大值时的时间点。
该模型在初始时,生长速度较快,随着时间的推移,生长速度逐渐减缓。
当N→∞时,N(N)趋近于最大生长速度N。
其次,参数估计是建立非线性成长模型的关键步骤之一。
参数估计的目标是通过已知的数据来估计模型中的参数值,使得模型与实际观测值之间的拟合程度最好。
估计非线性成长模型的参数存在多种方法,其中最常用的方法是最小二乘法。
最小二乘法通过最小化观测值与模型预测值之间的残差平方和来确定最优参数值。
在参数估计过程中,需要选择合适的初始参数值,将问题转化为一个最优化问题。
采用迭代的方式,不断调整参数值,直到找到最小的残差平方和。
此外,为了保证参数估计的稳定性和准确性,常常需要采用统计方法来评估模型的拟合度与参数的显著性。
常见的统计指标包括确定系数(R^2)、AIC(Akaike information criterion)和BIC(Bayesian information criterion)等。
确定系数可以衡量模型拟合数据的好坏,范围从0到1,值越接近1表示拟合效果越好。
非线性回归一、介绍线性回归是一种基本的统计方法,在许多领域中都有广泛的应用。
然而,在现实世界中,很多问题并不满足线性关系。
这时,非线性回归就成为了一种更加适用的方法。
二、非线性回归模型非线性回归模型是通过拟合非线性函数来描述自变量和因变量之间的关系。
一般来说,非线性回归模型可以分为参数模型和非参数模型。
1. 参数模型参数模型是指非线性函数中包含一些参数,通过最小化残差的平方和来估计这些参数的值。
常见的参数模型包括指数模型、幂函数模型、对数模型等。
2. 非参数模型非参数模型是指非线性函数中没有参数,通过直接拟合数据来建立模型。
常见的非参数模型包括样条函数模型、神经网络模型等。
三、非线性回归的应用非线性回归在许多领域中都有广泛的应用,特别是在生物学、经济学、工程学等领域中。
下面介绍几个非线性回归的应用实例:1. 生物学研究非线性回归在生物学研究中有很多应用,其中一个典型的例子是用来描述酶动力学的反应速率方程。
酶动力学研究中,根据酶底物浓度和反应速率的关系来建立非线性回归模型,从而研究酶的活性和底物浓度之间的关系。
2. 经济学分析非线性回归在经济学中也有许多应用,其中一个典型的例子是用来描述经济增长模型。
经济增长模型中,根据投资、人口增长率等因素来建立非线性回归模型,从而预测国家的经济增长趋势。
3. 工程学设计非线性回归在工程学设计中有很多应用,其中一个典型的例子是用来描述材料的应力-应变关系。
材料的应力-应变关系通常是非线性的,通过非线性回归模型可以更准确地描述材料的力学性能。
四、非线性回归的优缺点非线性回归相对于线性回归具有一些优点和缺点。
下面分别介绍:1. 优点非线性回归可以更准确地描述自变量和因变量之间的关系,适用于不满足线性关系的问题。
非线性回归的模型形式更灵活,可以通过选择适当的函数形式来更好地拟合数据。
2. 缺点非线性回归相比线性回归更复杂,需要更多的计算资源和时间。
非线性回归的参数估计也更加困难,需要依赖一些优化算法来找到最优解。
非线性模型与参数估计方法研究1.引言非线性模型是现代统计学中一个重要的分支,随着计算机性能的不断提高和数据维度的不断增加,非线性模型的应用正在越来越广泛。
在实际应用中,参数估计是非线性模型不可避免的一部分,而参数估计的精度对模型预测的准确性起着至关重要的作用。
在本文中,我们将介绍非线性模型及其参数估计方法的研究现状,并讨论其应用价值和发展趋势。
2.非线性模型非线性模型是指模型中自变量与因变量之间不满足线性关系的模型。
非线性模型一般在目标函数中引入一些非线性项,以适应复杂的实际情况。
在实际应用中,非线性模型的种类繁多,常见的有曲线拟合、非线性回归、广义线性模型等。
非线性模型既可以用于描述现象,又可以用于预测未来,具有很高的应用价值。
在非线性模型中,很多模型的参数是需要估计的。
3.参数估计方法参数估计是非线性模型中一个至关重要的问题,其精度直接关系到模型的预测准确性。
常见的参数估计方法有极大似然估计、最小二乘估计、贝叶斯估计等。
极大似然估计是一种计算方便、精度较高的方法,最小二乘估计则是样本量较大时最优的方法,而贝叶斯估计则可以自然地引入先验信息,使得估计结果更加准确。
此外,基于神经网络的参数估计方法和贪心算法也获得了一定的应用。
4.应用价值非线性模型及其参数估计方法在各种领域中都有着广泛的应用。
在金融领域,非线性模型可以用于股票价格的预测和交易决策的制定。
在医学领域,非线性模型可以用于疾病的诊断和治疗方案的优化。
在物流领域,非线性模型可以用于路线优化和成本控制。
随着社会经济的发展,非线性模型的应用范围将越来越广泛。
5.发展趋势随着计算机性能的不断提高,大数据分析和人工智能技术的应用越来越普及,非线性模型的应用前景更加广阔。
同时,非线性模型及其参数估计方法也在不断发展。
例如,基于深度学习的非线性模型已经取得了许多研究和应用成果。
此外,混沌理论、粒子群算法、受限玻尔兹曼机等技术也为非线性模型提供了新的思路和手段。
EViews非线性模型参数估计方法步骤
1.新建EViews工作区,并将时间序列X、P1和P0导入到工作区;
2.设定参数的初始值全部为1,其方法是在工作区中其输入下列命令
并按回车键
param c(1) 1 c(2) 1 c(3) 1 c(4) 1
3.估计非线性模型参数,其方法是在工作区中其输入下列命令并按
回车键
nls q=exp(c(1))*x^c(2)*p1^c(3)*p0^c(4)
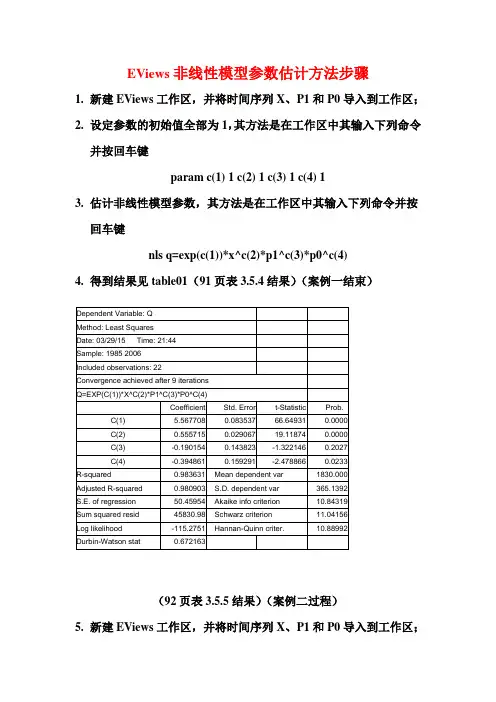
4.得到结果见table01(91页表3.
5.4结果)(案例一结束)
Dependent Variable: Q
Method: Least Squares
Date: 03/29/15 Time: 21:44
Sample: 1985 2006
Included observations: 22
Convergence achieved after 9 iterations
Q=EXP(C(1))*X^C(2)*P1^C(3)*P0^C(4)
Coefficient Std. Error t-Statistic Prob.
C(1) 5.567708 0.083537 66.64931 0.0000
C(2) 0.555715 0.029067 19.11874 0.0000
C(3) -0.190154 0.143823 -1.322146 0.2027
C(4) -0.394861 0.159291 -2.478866 0.0233
R-squared 0.983631 Mean dependent var 1830.000
Adjusted R-squared 0.980903 S.D. dependent var 365.1392
S.E. of regression 50.45954 Akaike info criterion 10.84319
Sum squared resid 45830.98 Schwarz criterion 11.04156
Log likelihood -115.2751 Hannan-Quinn criter. 10.88992
Durbin-Watson stat 0.672163
(92页表3.5.5结果)(案例二过程)
5.新建EViews工作区,并将时间序列X、P1和P0导入到工作区;
6.设定参数的初始值全部为1,其方法是在工作区中其输入下列命令
并按回车键
param c(1) 1 c(2) 1 c(3) 1
7.估计非线性模型参数,其方法是在工作区中其输入下列命令并按
回车键
nls q=exp(c(1))*(x/p0)^c(2)*(p1/p0)^c(3)
8.得到结果见table02(92页表3.5.5结果)(案例二结束)
Dependent Variable: Q
Method: Least Squares
Date: 03/29/15 Time: 22:14
Sample: 1985 2006
Included observations: 22
Convergence achieved after 4 iterations
Q=EXP(C(1))*(X/P0)^C(2)*(P1/P0)^C(3)
Coefficient Std. Error t-Statistic Prob.
C(1) 5.525965 0.072685 76.02666 0.0000
C(2) 0.533824 0.019785 26.98163 0.0000
C(3) -0.242862 0.134014 -1.812219 0.0858
R-squared 0.982669 Mean dependent var 1830.000
Adjusted R-squared 0.980845 S.D. dependent var 365.1392
S.E. of regression 50.53638 Akaike info criterion 10.80939
Sum squared resid 48524.59 Schwarz criterion 10.95817
Log likelihood -115.9033 Hannan-Quinn criter. 10.84444
Durbin-Watson stat 0.656740。