2018尺规作图2

[13.4 1•作一条线段等于已知线段 2.作一个角等于已知角]课堂达标、选择题1. 已知线段AB和CD用尺规作线段EF,使EF= A聊CD,第一步作射线EP,第二步（）A. 在射线EP上依次截取两条线段，分别等于AB和CDB. 用刻度尺量出AB和CD的长，再在EP上截取C. 在射线EP上截取两条线段，分别等于AB和CDD.延长AB到点D,使BD= AB2. 2017 •随州如图K—31 - 1,用尺规作图作/ AOO Z AOB的第一步是以点0为圆心,分别交OA 0B于点E, F,那么第二步的作图痕迹②的作法是A. 以点F为圆心,B. 以点F为圆心,C. 以点E为圆心,D. 以点E为圆心,0E长为半径画弧EF长为半径画弧0E长为半径画弧EF长为半径画弧A. S.S.S. B . S.A.S.用直尺和圆规作一个角等于已知角,的依据是（3.图K—31—1如图K—31 —2，能得出/ A O' B'=/ AOB以任意长为半径画弧①,C. A.S.A. D . A.A.S.、填空题图K—31 - 34•如图K- 31 —3,以点0为圆心，任意长为半径画弧，与射线0P交于点A再以点A为圆心，0A长为半径画弧，两弧交于点B，画射线0B则/ AOB= __________ ° .5.如图K—31 —4所示，已知线段a, c和/ a ,求作：△ ABC使BC= a, AB= c,Z ABC= Za ,根据作图过程(图K —31 —5),把下面的空格处填上适当的文字或字母.链接听课例4归纳总结图K—31 —4图K—31 —5⑴如图K—31 —4①所示，作Z MBI4 ________ ;(2)如图②所示，在射线BM上截取BC= _________ ，在射线BN上截取BA= ________(3)连结AC如图③所示，__________ 就是所求作的三角形.三、解答题6.如图K—31 —6所示，光线CO照射到平面镜AB上的点0,请你用尺规作出光线CO 经过平面镜反射后的光线.(保留作图痕迹，不写作法)链接听课例4归纳总结。

第24讲 尺规作图1．尺规作图的作图工具 圆规和没有刻度的直尺 2．基本尺规作图类型一：作一条线段等于已知线段 步骤：①作射线OP ；②以O 为圆心，a 为半径作弧，交OP 于A ，OA 即为所求线段．图示：类型三：作线段的垂直平分线步骤：①分别以点A ，B 为圆心，以大于12AB 长为半径，在AB 两侧作弧，两弧交于M ，N 点；②连接MN ，直线MN 即为所求垂直平分线．图示：类型四：作一个角等于已知角：步骤：①以O 为圆心，以任意长为半径作弧，交∠α的两边于点P ，Q ； ②作射线O′A ；③以O′为圆心，OP 长为半径作弧，交O′A 于点M ； ④以点M 为圆心，PQ 长为半径作弧，交前弧于点N ； ⑤过点N 作射线O′B ，∠AO′B 即为所求角．图示：类型五：过一点作已知直线的垂线步骤：点在直线上：①以点O 为圆心，任意长为半径作弧，交直线于A ，B 两点； ②分别以点A ，B 为圆心，以大于12AB 长为半径在直线两侧作弧，交点分别为M ，N ；③连接MN ，MN 即为所求垂线． 点在直线外：①在直线另一侧取点M ； ②以PM 为半径画弧，交直线于A ，B 两点；③分别以A ，B 为圆心，以大于12AB 长为半径画弧，交M 同侧于点N ；④连接PN ，则直线PN 即为所求的垂线．图示：3．常见几种基本尺规作图作三角形 ①已知三边作三角形； ②已知两边及其夹角作三角形； ③已知两角及其夹边作三角形； ④已知底边及底边上的高作等腰三角形； ⑤已知一直角边和斜边作直角三角形． 4．作图的一般步骤(1)已知；(2)求作；(3)分析；(4)作法；(5)证明； (6)讨论．步骤(5)(6)常不作要求，步骤(3)一般不要求，但作图中一定要保留作图痕迹.考点1：简单尺规作图【例题1】尺规作图，已知顶角和底边上的高，求作等腰三角形． 已知：如图，∠α，线段a.求作：△ABC ，使AB ＝AC ，∠BAC ＝α，AD ⊥BC 于D ，且AD ＝a.【解析】：作图如图，(1)作∠EAF ＝∠α；(2)作AG 平分∠EAF ，并在AG 上截取AD ＝a ；(3)过D 作MN ⊥AG ，MN 与AE ，AF 分别交于B ，C.则△ABC 即为所求作的等腰三角形归纳：1．熟悉五个基本的作图步骤及作图痕迹． 2．平时多体会和理解一些复杂作图的依据及作图过程． 3．会在常见的作图语言与对应的几何语言之间进行转化．4．提倡在平时画图时，采用尺规作图，强化自己的作图意识和规范性． 考点2： 复杂尺规作图【例题2】如图，在△ABC 中，已知∠ABC ＝90°.(1)请在BC 上找一点P ，作⊙P 与AC ，AB 都相切，与AC 的切点为Q ；(尺规作图，保留作图痕迹) (2)连接BQ ，若AB ＝3，(1)中所作圆的半径为32，求sin ∠CBQ.【分析】 (1)要求作⊙P 与AB 、AC 相切，根据切线的性质，即点P 到AB 、AC 的距离相等，且点P 在边BC 上，想到角平分线上的点到角两边的距离相等，即作∠BAC 的平分线交BC 于P 点，以点P 为圆心，PB 为半径作圆即可；(2)由切线长定理得AB ＝AQ ，又PB ＝PQ ，则判定AP 为BQ 的垂直平分线，利用等角的余角相等得到∠CBQ ＝∠BAP ，然后在Rt △ABP 中利用正弦函数求出sin ∠BAP ，从而可得到sin ∠CBQ 的值．解：(1)如图所示，⊙P 即为所求：(2)∵AB 、AQ 为⊙P 的切线，∴AB ＝AQ ，∵PB ＝PQ ，∴AP 为BQ 的垂直平分线，∴∠BAP ＋∠ABQ ＝90°，∵∠CBQ ＋∠ABQ ＝90°，∴∠CBQ ＝∠BAP ，在Rt △ABP 中，AP ＝AB 2＋PB 2＝32＋（32）2＝352，∴sin ∠BAP ＝BP AP ＝32352＝55，∴sin ∠CBQ ＝55考点3： 关于尺规作图的应用【例题3】（2019▪广西池河▪8分）如图，AB 为⊙O 的直径，点C 在⊙O 上．（1）尺规作图：作∠BAC 的平分线，与⊙O 交于点D ；连接OD ，交BC 于点E （不写作法，只保留作图痕迹，且用黑色墨水笔将作图痕迹加黑）；（2）探究OE 与AC 的位置及数量关系，并证明你的结论．【分析】（1）利用基本作图作AD 平分∠BAC ，然后连接OD 得到点E ；（2）由AD 平分∠BAC 得到∠BAD ＝12∠BAC ，由圆周角定理得到∠BAD ＝12∠BOD ，则∠BOD ＝∠BAC ，再证明OE 为△ABC 的中位线，从而得到OE ∥AC ，OE ＝12AC ．【解答】解：（1）如图所示；（2）OE∥AC，OE＝12 AC．理由如下：∵AD平分∠BAC，∴∠BAD＝12∠BAC，∵∠BAD＝12∠BOD，∴∠BOD＝∠BAC，∴OE∥AC，∵OA＝OB，∴OE为△ABC的中位线，∴OE∥AC，OE＝12 AC．一、选择题：1.（2018年湖北省宜昌市3分）尺规作图：经过已知直线外一点作这条直线的垂线，下列作图中正确的是（）A．B．C．D．【答案】B【解答】已知：直线AB和AB外一点C．求作：AB的垂线，使它经过点C．作法：（1）任意取一点K，使K和C在AB的两旁．（2）以C为圆心，CK的长为半径作弧，交AB于点D和E．（3）分别以D和E为圆心，大于DE的长为半径作弧，两弧交于点F，（4）作直线CF．直线CF就是所求的垂线．故选：B．2. （2018•襄阳）如图，在△ABC中，分别以点A和点C为圆心，大于AC长为半径画弧，两弧相交于点M，N，作直线MN分别交BC，AC于点D，E．若AE=3cm，△ABD的周长为13cm，则△ABC的周长为（）A．16cm B．19cm C．22cm D．25cm【答案】B【解答】解：∵DE垂直平分线段AC，∴DA=DC，AE=EC=6cm，∵AB+AD+BD=13cm，∴AB+BD+DC=13cm，∴△ABC的周长=AB+BD+BC+AC=13+6=19cm，故选：B．3. （2019•河北•3分）根据圆规作图的痕迹，可用直尺成功找到三角形外心的是（）A．B．C．D．【答案】C【解答】解：三角形外心为三边的垂直平分线的交点，由基本作图得到C选项作了两边的垂直平分线，从而可用直尺成功找到三角形外心．故选：C．4. （2019•贵阳•3分）如图，在△ABC中，AB＝AC，以点C为圆心，CB长为半径画弧，交AB于点B和点D，再分别以点B，D为圆心，大于BD长为半径画弧，两弧相交于点M，作射线CM交AB于点E．若AE＝2，BE＝1，则EC的长度是（）A．2 B．3 C．D．【答案】D【解答】解：由作法得CE⊥AB，则∠AEC＝90°，AC＝AB＝BE+AE＝2+1＝3，在Rt△ACE中，CE＝＝．故选：D．5. （2018•河南）如图，已知▱AOBC的顶点O（0，0），A（﹣1，2），点B在x轴正半轴上按以下步骤作图：①以点O为圆心，适当长度为半径作弧，分别交边OA，OB于点D，E；②分别以点D，E为圆心，大于DE的长为半径作弧，两弧在∠AOB内交于点F；③作射线OF，交边AC于点G，则点G的坐标为（）A．（﹣1，2）B．（，2）C．（3﹣，2）D．（﹣2，2）【答案】A【解答】解：∵▱AOBC的顶点O（0，0），A（﹣1，2），∴AH=1，HO=2，∴Rt△AOH中，AO=，由题可得，OF平分∠AOB，∴∠AOG=∠EOG，又∵AG∥OE，∴∠AGO=∠EOG，∴∠AGO=∠AOG，∴AG=AO=，∴HG=﹣1，∴G（﹣1，2），故选：A．二、填空题：6. （2018•南京）如图，在△ABC中，用直尺和圆规作AB、AC的垂直平分线，分别交AB、AC于点D、E，连接DE．若BC=10cm，则DE=cm．【答案】5【解答】解：∵用直尺和圆规作AB、AC的垂直平分线，∴D为AB的中点，E为AC的中点，∴DE是△ABC的中位线，∴DE=BC=5cm．故答案为：5．7. （2019•河南•3分）如图，在四边形ABCD中，AD∥BC，∠D＝90°，AD＝4，BC＝3．分别以点A，C为圆心，大于12AC长为半径作弧，两弧交于点E，作射线BE交AD于点F，交AC于点O．若点O是AC的中点，则CD的长为.【答案】22．【解答】解：如图，连接FC，则AF＝FC．∵AD∥BC，∴∠F AO＝∠BCO．在△FOA与△BOC中，，∴△FOA≌△BOC（ASA），∴AF＝BC＝3，∴FC＝AF＝3，FD＝AD﹣AF＝4﹣3＝1．在△FDC中，∵∠D＝90°，∴CD2+DF2＝FC2，∴CD2+12＝32，∴CD＝2．8. （2018•淮安）如图，在Rt△ABC中，∠C=90°，AC=3，BC=5，分别以点A、B为圆心，大于AB的长为半径画弧，两弧交点分别为点P、Q，过P、Q两点作直线交BC于点D，则CD的长是．【答案】【解答】解：连接AD．∵PQ垂直平分线段AB，∴DA=DB，设DA=DB=x，在Rt△ACD中，∠C=90°，AD2=AC2+CD2，∴x2=32+（5﹣x）2，解得x=，∴CD=BC ﹣DB=5﹣=，故答案为． 三、解答题：9. 2.如图，在Rt △ABC 中，∠ACB ＝90°.(1)利用直尺和圆规按下列要求作图，并在图中标明相应的字母．(保留作图痕迹，不写作法) ①作AC 的垂直平分线，交AB 于点O ，交AC 于点D; ②以O 为圆心，OA 为半径作圆，交OD 的延长线于点E. (2)在(1)所作的图形中，解答下列问题.①点B 与⊙O 的位置关系是_____________；(直接写出答案) ②若DE ＝2，AC ＝8，求⊙O 的半径．解：(1)如图所示： (2)①连接OC ，如图，∵OD 垂直平分AC ，∴OA ＝OC ，∴∠A ＝∠ACO ，∵∠A ＋∠B ＝90°，∠OCB ＋∠ACO ＝90°，∴∠B ＝∠OCB ，∴OC ＝OB ，∴OB ＝OA ，∴点B 在⊙O 上； ②∵OD ⊥AC ，且点D 是AC 的中点，∴AD ＝12AC ＝4，设⊙O 的半径为r ，则OA ＝OE ＝r ，OD ＝OE －DE ＝r －2，在Rt △AOD 中，∵OA 2＝AD 2＋OD 2，即r 2＝42＋(r －2)2，解得r ＝5.∴⊙O 的半径为510. （2018•安徽•分） 如图，⊙O 为锐角△ABC 的外接圆，半径为5.（1）用尺规作图作出∠BAC 的平分线，并标出它与劣弧BC 的交点E(保留作图痕迹，不写作法)； （2）若（1）中的点E 到弦BC 的距离为3，求弦CE 的长.【答案】（1）画图见解析；（2）CE=【解析】【分析】（1）以点A为圆心，以任意长为半径画弧，分别与AB、AC有交点，再分别以这两个交点为圆心，以大于这两点距离的一半为半径画弧，两弧交于一点，过点A与这点作射线，与圆交于点E ，据此作图即可；（2）连接OE交BC于点F，连接OC、CE，由AE平分∠BAC，可推导得出OE⊥BC，然后在Rt△OFC 中，由勾股定理可求得FC的长，在Rt△EFC中，由勾股定理即可求得CE的长.【详解】（1）如图所示，射线AE就是所求作的角平分线；（2）连接OE交BC于F，连接OC，如图，∵AE平分∠BAC，∴∠BAE＝∠CAE，∴＝，∴OE⊥BC，∴EF＝3，∴OF＝5﹣3＝2，在Rt△OCF中，CF＝＝，在Rt△CEF中，CE＝＝．11. （2019•江苏泰州•8分）如图，△ABC中，∠C＝90°，AC＝4，BC＝8．（1）用直尺和圆规作AB的垂直平分线；（保留作图痕迹，不要求写作法）（2）若（1）中所作的垂直平分线交BC于点D，求BD的长．【分析】（1）分别以A，B为圆心，大于12AB为半径画弧，两弧交于点M，N，作直线MN即可．（2）设AD＝BD＝x，在Rt△ACD中，利用勾股定理构建方程即可解决问题．【解答】解：（1）如图直线MN即为所求．（2）∵MN垂直平分线段AB，∴DA＝DB，设DA＝DB＝x，在Rt△ACD中，∵AD2＝AC2+CD2，∴x2＝42+（8﹣x）2，解得x＝5，∴BD＝5．12. （2018·广东·6分）如图，BD是菱形ABCD的对角线，∠CBD=75°，（1）请用尺规作图法，作AB的垂直平分线EF，垂足为E，交AD于F；（不要求写作法，保留作图痕迹）（2）在（1）条件下，连接BF，求∠DBF的度数．【分析】（1）分别以A、B为圆心，大于AB长为半径画弧，过两弧的交点作直线即可；（2）根据∠DBF=∠ABD﹣∠ABF计算即可；【解答】解：（1）如图所示，直线EF即为所求；（2）∵四边形ABCD是菱形，∴∠ABD=∠DBC=∠ABC=75°，DC∥AB，∠A=∠C．∴∠ABC=150°，∠ABC+∠C=180°，∴∠C=∠A=30°，∵EF垂直平分线线段AB，∴AF=FB，∴∠A=∠FBA=30°，∴∠DBF=∠ABD﹣∠FBE=45°．13. （2019•湖北孝感•8分）如图，Rt△ABC中，∠ACB＝90°，一同学利用直尺和圆规完成如下操作：①以点C为圆心，以CB为半径画弧，交AB于点G；分别以点G、B为圆心，以大于GB的长为半径画弧，两弧交点K，作射线CK；②以点B为圆心，以适当的长为半径画弧，交BC于点M，交AB的延长线于点N；分别以点M、N为圆心，以大于MN的长为半径画弧，两弧交于点P，作直线BP交AC的延长线于点D，交射线CK于点E．请你观察图形，根据操作结果解答下列问题；（1）线段CD与CE的大小关系是CD＝CE；（2）过点D作DF⊥AB交AB的延长线于点F，若AC＝12，BC＝5，求tan∠DBF的值．【分析】（1）由作图知CE⊥AB，BD平分∠CBF，据此得∠1＝∠2＝∠3，结合∠CEB+∠3＝∠2+∠CDE＝90°知∠CEB＝∠CDE，从而得出答案；（2）证△BCD≌△BFD得CD＝DF，从而设CD＝DF＝x，求出AB＝13，知sin∠DAF＝DFAD＝BCAB，即12+xx＝513，解之求得x＝152，结合BC＝BF＝5可得答案．【解答】解：（1）CD＝CE，由作图知CE⊥AB，BD平分∠CBF，∴∠1＝∠2＝∠3，∵∠CEB+∠3＝∠2+∠CDE＝90°，∴∠CEB＝∠CDE，∴CD＝CE，故答案为：CD＝CE；（2）∵BD平分∠CBF，BC⊥CD，BF⊥DF，∴BC＝BF，∠CBD＝∠FBD，在△BCD和△BFD中，∵，∴△BCD≌△BFD（AAS），∴CD＝DF，设CD＝DF＝x，在Rt△ACB中，AB＝13，∴sin∠DAF＝DFAD＝BCAB，即12+xx＝513，解得x＝152，∵BC＝BF＝5，∴tan∠DBF＝DFBF＝152×15＝32．。

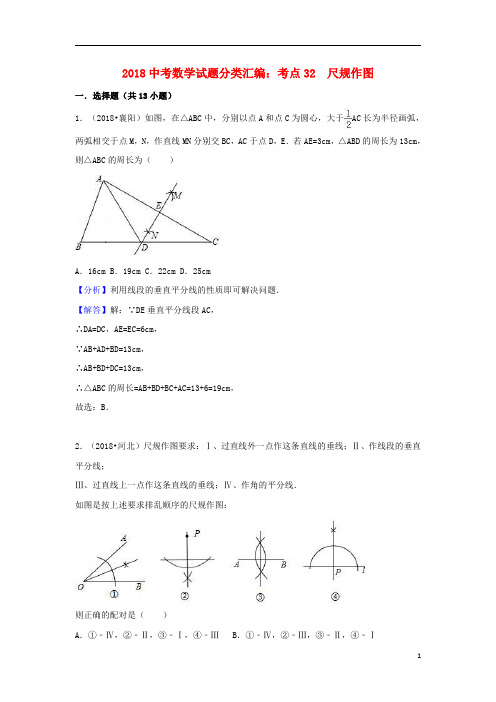
2018中考数学试题分类汇编：考点32尺规作图一．选择题（共13小题）1．（2018•襄阳）如图，在△ABC中，分别以点A和点C为圆心，大于AC长为半径画弧，两弧相交于点M，N，作直线MN分别交BC，AC于点D，E．若AE=3cm，△ABD的周长为13cm，则△ABC的周长为（）A．16cm B．19cm C．22cm D．25cm【分析】利用线段的垂直平分线的性质即可解决问题．【解答】解：∵DE垂直平分线段AC，∴DA=DC，AE=EC=6cm，∵AB+AD+BD=13cm，∴AB+BD+DC=13cm，∴△ABC的周长=AB+BD+BC+AC=13+6=19cm，故选：B．2．（2018•河北）尺规作图要求：Ⅰ、过直线外一点作这条直线的垂线；Ⅱ、作线段的垂直平分线；Ⅲ、过直线上一点作这条直线的垂线；Ⅳ、作角的平分线．如图是按上述要求排乱顺序的尺规作图：则正确的配对是（）A．①﹣Ⅳ，②﹣Ⅱ，③﹣Ⅰ，④﹣ⅢB．①﹣Ⅳ，②﹣Ⅲ，③﹣Ⅱ，④﹣ⅠC．①﹣Ⅱ，②﹣Ⅳ，③﹣Ⅲ，④﹣ⅠD．①﹣Ⅳ，②﹣Ⅰ，③﹣Ⅱ，④﹣Ⅲ【分析】分别利用过直线外一点作这条直线的垂线作法以及线段垂直平分线的作法和过直线上一点作这条直线的垂线、角平分线的作法分别得出符合题意的答案．【解答】解：Ⅰ、过直线外一点作这条直线的垂线；Ⅱ、作线段的垂直平分线；Ⅲ、过直线上一点作这条直线的垂线；Ⅳ、作角的平分线．如图是按上述要求排乱顺序的尺规作图：则正确的配对是：①﹣Ⅳ，②﹣Ⅰ，③﹣Ⅱ，④﹣Ⅲ．故选：D．3．（2018•河南）如图，已知▱AOBC的顶点O（0，0），A（﹣1，2），点B在x轴正半轴上按以下步骤作图：①以点O为圆心，适当长度为半径作弧，分别交边OA，OB于点D，E；②分别以点D，E为圆心，大于DE的长为半径作弧，两弧在∠AOB内交于点F；③作射线OF，交边AC于点G，则点G的坐标为（）A．（﹣1，2）B．（，2）C．（3﹣，2）D．（﹣2，2）【分析】依据勾股定理即可得到Rt△AOH中，AO=，依据∠AGO=∠AOG，即可得到AG=AO=，进而得出HG=﹣1，可得G（﹣1，2）．【解答】解：∵▱AOBC的顶点O（0，0），A（﹣1，2），∴AH=1，HO=2，∴Rt△AOH中，AO=，由题可得，OF平分∠AOB，∴∠AOG=∠EOG，又∵AG∥OE，∴∠AGO=∠EOG，∴∠AGO=∠AOG，∴AG=AO=，∴HG=﹣1，∴G（﹣1，2），故选：A．4．（2018•宜昌）尺规作图：经过已知直线外一点作这条直线的垂线，下列作图中正确的是（）A．B．C．D．【分析】根据过直线外一点向直线作垂线即可．【解答】已知：直线AB和AB外一点C．求作：AB的垂线，使它经过点C．作法：（1）任意取一点K，使K和C在AB的两旁．（2）以C为圆心，CK的长为半径作弧，交AB于点D和E．（3）分别以D和E为圆心，大于DE的长为半径作弧，两弧交于点F，（4）作直线CF．直线CF就是所求的垂线．故选：B．5．（2018•潍坊）如图，木工师傅在板材边角处作直角时，往往使用“三弧法”，其作法是：（1）作线段AB，分别以A，B为圆心，以AB长为半径作弧，两弧的交点为C；（2）以C为圆心，仍以AB长为半径作弧交AC的延长线于点D；（3）连接BD，BC．下列说法不正确的是（）A．∠CBD=30°B．S=AB2△BDCC．点C是△ABD的外心D．sin2A+cos2D=1【分析】根据等边三角形的判定方法，直角三角形的判定方法以及等边三角形的性质，直角三角形的性质一一判断即可；【解答】解：由作图可知：AC=AB=BC，∴△ABC是等边三角形，由作图可知：CB=CA=CD，∴点C是△ABD的外心，∠ABD=90°，BD=AB，=AB2，∴S△ABD∵AC=CD，∴S=AB2，△BDC故A、B、C正确，故选：D．6．（2018•郴州）如图，∠AOB=60°，以点O为圆心，以任意长为半径作弧交OA，OB于C，D两点；分别以C，D为圆心，以大于CD的长为半径作弧，两弧相交于点P；以O为端点作射线OP，在射线OP上截取线段OM=6，则M点到OB的距离为（）A．6B．2C．3D．【分析】直接利用角平分线的作法得出OP是∠AOB的角平分线，再利用直角三角形的性质得出答案．【解答】解：过点M作ME⊥OB于点E，由题意可得：OP是∠AOB的角平分线，则∠POB=×60°=30°，∴ME=OM=3．故选：C．7．（2018•台州）如图，在▱ABCD中，AB=2，BC=3．以点C为圆心，适当长为半径画弧，交BC于点P，交CD于点Q，再分别以点P，Q为圆心，大于PQ的长为半径画弧，两弧相交于点N，射线CN交BA的延长线于点E，则AE的长是（）A．B．1C．D．【分析】只要证明BE=BC即可解决问题；【解答】解：∵由题意可知CF是∠BCD的平分线，∴∠BCE=∠DCE．∵四边形ABCD是平行四边形，∴AB∥CD，∴∠DCE=∠E，∠BCE=∠AEC，∴BE=BC=3，∵AB=2，∴AE=BE﹣AB=1，故选：B．8．（2018•嘉兴）用尺规在一个平行四边形内作菱形ABCD，下列作法中错误的是（）A．B．C．D．【分析】根据菱形的判定和作图根据解答即可．【解答】解：A、由作图可知，AC⊥BD，且平分BD，即对角线平分且垂直的四边形是菱形，正确；B、由作图可知AB=BC，AD=AB，即四边相等的四边形是菱形，正确；C、由作图可知AB=DC，AD=BC，只能得出ABCD是平行四边形，错误；D、由作图可知对角线AC平分对角，可以得出是菱形，正确；故选：C．9．（2018•昆明）如图，点A在双曲线y═（x＞0）上，过点A作AB⊥x轴，垂足为点B，分别以点O和点A为圆心，大于OA的长为半径作弧，两弧相交于D，E两点，作直线DE 交x轴于点C，交y轴于点F（0，2），连接AC．若AC=1，则k的值为（）A．2B．C．D．【分析】如图，设OA交CF于K．利用面积法求出OA的长，再利用相似三角形的性质求出AB、OB即可解决问题；【解答】解：如图，设OA交CF于K．由作图可知，CF垂直平分线段OA，∴OC=CA=1，OK=AK，在Rt△OFC中，CF==，∴AK=OK==，∴OA=，由△FOC∽△OBA，可得==，∴==，∴OB=，AB=，∴A（，），∴k=．故选：B．10．（2018•湖州）尺规作图特有的魅力曾使无数人沉湎其中．传说拿破仑通过下列尺规作图考他的大臣：①将半径为r的⊙O六等分，依次得到A，B，C，D，E，F六个分点；②分别以点A，D为圆心，AC长为半径画弧，G是两弧的一个交点；③连结OG．问：OG的长是多少？大臣给出的正确答案应是（）A．rB．（1+）r C．（1+）r D．r【分析】如图连接CD，AC，DG，AG．在直角三角形即可解决问题；【解答】解：如图连接CD，AC，DG，AG．∵AD是⊙O直径，∴∠ACD=90°，在Rt△ACD中，AD=2r，∠DAC=30°，∴AC=r，∵DG=AG=CA，OD=OA，∴OG⊥AD，∴∠GOA=90°，∴OG===r，故选：D．11．（2018•台湾）如图，锐角三角形ABC中，BC＞AB＞AC，甲、乙两人想找一点P，使得∠BPC与∠A互补，其作法分别如下：（甲）以A为圆心，AC长为半径画弧交AB于P点，则P即为所求；（乙）作过B点且与AB垂直的直线l，作过C点且与AC垂直的直线，交l于P点，则P即为所求对于甲、乙两人的作法，下列叙述何者正确？（）A．两人皆正确B．两人皆错误C．甲正确，乙错误D．甲错误，乙正确【分析】甲：根据作图可得AC=AP，利用等边对等角得：∠APC=∠ACP，由平角的定义可知：∠BPC+∠APC=180°，根据等量代换可作判断；乙：根据四边形的内角和可得：∠BPC+∠A=180°．【解答】解：甲：如图1，∵AC=AP，∴∠APC=∠ACP，∵∠BPC+∠APC=180°∴∠BPC+∠ACP=180°，∴甲错误；乙：如图2，∵AB⊥PB，AC⊥PC，∴∠ABP=∠ACP=90°，∴∠BPC+∠A=180°，∴乙正确，故选：D．12．（2018•安顺）已知△ABC（AC＜BC），用尺规作图的方法在BC上确定一点P，使PA+PC=BC，则符合要求的作图痕迹是（）A．B．C．D．【分析】利用线段垂直平分线的性质以及圆的性质分别分得出即可．【解答】解：A、如图所示：此时BA=BP，则无法得出AP=BP，故不能得出PA+PC=BC，故此选项错误；B、如图所示：此时PA=PC，则无法得出AP=BP，故不能得出PA+PC=BC，故此选项错误；C、如图所示：此时CA=CP，则无法得出AP=BP，故不能得出PA+PC=BC，故此选项错误；D、如图所示：此时BP=AP，故能得出PA+PC=BC，故此选项正确；故选：D．13．（2017•南宁）如图，△ABC中，AB＞AC，∠CAD为△ABC的外角，观察图中尺规作图的痕迹，则下列结论错误的是（）A．∠DAE=∠B B．∠EAC=∠C C．AE∥BC D．∠DAE=∠EAC【分析】根据图中尺规作图的痕迹，可得∠DAE=∠B，进而判定AE∥BC，再根据平行线的性质即可得出结论．【解答】解：根据图中尺规作图的痕迹，可得∠DAE=∠B，故A选项正确，∴AE∥BC，故C选项正确，∴∠EAC=∠C，故B选项正确，∵AB＞AC，∴∠C＞∠B，∴∠CAE＞∠DAE，故D选项错误，故选：D．二．填空题（共7小题）14．（2018•南京）如图，在△ABC中，用直尺和圆规作AB、AC的垂直平分线，分别交AB、AC于点D、E，连接DE．若BC=10cm，则DE=5cm．【分析】直接利用线段垂直平分线的性质得出DE是△ABC的中位线，进而得出答案．【解答】解：∵用直尺和圆规作AB、AC的垂直平分线，∴D为AB的中点，E为AC的中点，∴DE是△ABC的中位线，∴DE=BC=5cm．故答案为：5．15．（2018•淮安）如图，在Rt△ABC中，∠C=90°，AC=3，BC=5，分别以点A、B为圆心，大于AB的长为半径画弧，两弧交点分别为点P、Q，过P、Q两点作直线交BC于点D，则CD的长是．【分析】连接AD由PQ垂直平分线段AB，推出DA=DB，设DA=DB=x，在Rt△ACD中，∠C=90°，根据AD2=AC2+CD2构建方程即可解决问题；【解答】解：连接AD．∵PQ垂直平分线段AB，∴DA=DB，设DA=DB=x，在Rt△ACD中，∠C=90°，AD2=AC2+CD2，∴x2=32+（5﹣x）2，解得x=，∴CD=BC﹣DB=5﹣=，故答案为．16．（2018•山西）如图，直线MN∥PQ，直线AB分别与MN，PQ相交于点A，B．小宇同学利用尺规按以下步骤作图：①以点A为圆心，以任意长为半径作弧交AN于点C，交AB于点D；②分别以C，D为圆心，以大于CD长为半径作弧，两弧在∠NAB内交于点E；③作射线AE交PQ于点F．若AB=2，∠ABP=60°，则线段AF的长为2．【分析】作高线BG，根据直角三角形30度角的性质得：BG=1，AG=，可得AF的长．【解答】解：∵MN∥PQ，∴∠NAB=∠ABP=60°，由题意得：AF平分∠NAB，∴∠1=∠2=30°，∵∠ABP=∠1+∠3，∴∠3=30°，∴∠1=∠3=30°，∴AB=BF，AG=GF，∵AB=2，∴BG=AB=1，∴AG=，∴AF=2AG=2，故答案为：2．17．（2018•东营）如图，在Rt△ABC 中，∠B=90°，以顶点C 为圆心，适当长为半径画弧，分别交AC，BC 于点E，F，再分别以点E，F 为圆心，大于EF 的长为半径画弧，两弧交于点P，作射线CP 交AB 于点D．若BD=3，AC=10，则△ACD 的面积是15．【分析】作DQ⊥AC，由角平分线的性质知DB=DQ=3，再根据三角形的面积公式计算可得．【解答】解：如图，过点D 作DQ⊥AC 于点Q，由作图知CP 是∠ACB 的平分线，∵∠B=90°，BD=3，∴DB=DQ=3，∵AC=10，∴S △ACD =•AC•DQ=×10×3=15，故答案为：15．18．（2018•通辽）如图，在△ABC 中，按以下步骤作图：①分别以点A 和点C 为圆心，以大于AC 的长为半径作弧，两弧相交于M、N 两点；②作直线MN 交BC 于点D，连接AD．若AB=BD，AB=6，∠C=30°，则△ACD 的面积为9．【分析】只要证明△ABD 是等边三角形，推出BD=AD=DC，可得S △ADC =S △ABD 即可解决问题；【解答】解：由作图可知，MN 垂直平分线段AC，∴DA=DC，∴∠C=∠DAC=30°，∴∠ADB=∠C+∠DAC=60°，∵AB=AD，∴△ABD 是等边三角形，∴BD=AD=DC，∴S △ADC =S △ABD =×62=9，故答案为9．19．（2018•成都）如图，在矩形ABCD 中，按以下步骤作图：①分别以点A 和C 为圆心，以大于AC 的长为半径作弧，两弧相交于点M 和N；②作直线MN 交CD 于点E．若DE=2，CE=3，则矩形的对角线AC 的长为．【分析】连接AE，如图，利用基本作图得到MN 垂直平分AC，则EA=EC=3，然后利用勾股定理先计算出AD，再计算出AC．【解答】解：连接AE，如图，由作法得MN 垂直平分AC，∴EA=EC=3，在Rt△ADE 中，AD==，在Rt△ADC 中，AC==．故答案为．20．（2018•湖州）在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点．以顶点都是格点的正方形ABCD的边为斜边，向内作四个全等的直角三角形，使四个直角顶点E，F，G，H都是格点，且四边形EFGH为正方形，我们把这样的图形称为格点弦图．例如，在如图1所示的格点弦图中，正方形ABCD的边长为，此时正方形EFGH的而积为5．问：当格点弦图中的正方形ABCD的边长为时，正方形EFGH的面积的所有可能值是13或49或9（不包括5）．【分析】当DG=，CG=2时，满足DG2+CG2=CD2，此时HG=，可得正方形EFGH的面积为13．当DG=8，CG=1时，满足DG2+CG2=CD2，此时HG=7，可得正方形EFGH的面积为49．当DG=7，CG=4时，满足DG2+CG2=CD2，此时HG=3，可得正方形EFGH的面积为9．【解答】解：当DG=，CG=2时，满足DG2+CG2=CD2，此时HG=，可得正方形EFGH 的面积为13．当DG=8，CG=1时，满足DG2+CG2=CD2，此时HG=7，可得正方形EFGH的面积为49．当DG=7，CG=4时，满足DG2+CG2=CD2，此时HG=3，可得正方形EFGH的面积为9．故答案为13或49或9．三．解答题（共21小题）21．（2018•广州）如图，在四边形ABCD中，∠B=∠C=90°，AB＞CD，AD=AB+CD．（1）利用尺规作∠ADC的平分线DE，交BC于点E，连接AE（保留作图痕迹，不写作法）；（2）在（1）的条件下，①证明：AE⊥DE；②若CD=2，AB=4，点M，N分别是AE，AB上的动点，求BM+MN的最小值．【分析】（1）利用尺规作出∠ADC的角平分线即可；（2）①延长DE交AB的延长线于F．只要证明AD=AF，DE=EF，利用等腰三角形三线合一的性质即可解决问题；②作点B关于AE的对称点K，连接EK，作KH⊥AB于H，DG⊥AB于G．连接MK．由MB=MK，推出MB+MN=KM+MN，根据垂线段最短可知：当K、M、N共线，且与KH重合时，KM+MN的值最小，最小值为KH的长；【解答】解：（1）如图，∠ADC的平分线DE如图所示．（2）①延长DE交AB的延长线于F．∵CD∥AF，∴∠CDE=∠F，∵∠CDE=∠ADE，∴∠ADF=∠F，∴AD=AF，∵AD=AB+CD=AB+BF，∴CD=BF，∵∠DEC=∠BEF，∴△DEC≌△FEB，∴DE=EF，∵AD=AF，∴AE⊥DE．②作点B关于AE的对称点K，连接EK，作KH⊥AB于H，DG⊥AB于G．连接MK．∵AD=AF，DE=EF，∴AE平分∠DAF，则△AEK≌△AEB，∴AK=AB=4，在Rt△ADG中，DG==4，∵KH∥DG，∴=，∴=，∴KH=，∵MB=MK，∴MB+MN=KM+MN，∴当K、M、N共线，且与KH重合时，KM+MN的值最小，最小值为KH的长，∴BM+MN的最小值为．22．（2018•广东）如图，BD是菱形ABCD的对角线，∠CBD=75°，（1）请用尺规作图法，作AB的垂直平分线EF，垂足为E，交AD于F；（不要求写作法，保留作图痕迹）（2）在（1）条件下，连接BF，求∠DBF的度数．【分析】（1）分别以A、B为圆心，大于AB长为半径画弧，过两弧的交点作直线即可；（2）根据∠DBF=∠ABD﹣∠ABF计算即可；【解答】解：（1）如图所示，直线EF即为所求；（2）∵四边形ABCD是菱形，∴∠ABD=∠DBC=∠ABC=75°，DC∥AB，∠A=∠C．∴∠ABC=150°，∠ABC+∠C=180°，∴∠C=∠A=30°，∵EF垂直平分线线段AB，∴AF=FB，∴∠A=∠FBA=30°，∴∠DBF=∠ABD﹣∠FBE=45°．23．（2018•安徽）如图，⊙O为锐角△ABC的外接圆，半径为5．（1）用尺规作图作出∠BAC的平分线，并标出它与劣弧的交点E（保留作图痕迹，不写作法）；（2）若（1）中的点E到弦BC的距离为3，求弦CE的长．【分析】（1）利用基本作图作AE平分∠BAC；（2）连接OE交BC于F，连接OC，如图，根据圆周角定理得到=，再根据垂径定理得到OE⊥BC，则EF=3，OF=2，然后在Rt△OCF中利用勾股定理计算出CF=，在Rt△CEF中利用勾股定理可计算出CE．【解答】解：（1）如图，AE为所作；（2）连接OE交BC于F，连接OC，如图，∵AE平分∠BAC，∴∠BAE=∠CAE，∴=，∴OE⊥BC，∴EF=3，∴OF=5﹣3=2，在Rt△OCF中，CF==，在Rt△CEF中，CE==．24．（2018•自贡）如图，在△ABC中，∠ACB=90°．（1）作出经过点B，圆心O在斜边AB上且与边AC相切于点E的⊙O（要求：用尺规作图，保留作图痕迹，不写作法和证明）（2）设（1）中所作的⊙O与边AB交于异于点B的另外一点D，若⊙O的直径为5，BC=4；求DE的长．（如果用尺规作图画不出图形，可画出草图完成（2）问）【分析】（1）作∠ABC的角平分线交AC于E，作EO⊥AC交AB于点O，以O为圆心，OB为半径画圆即可解决问题；（2）作OH⊥BC于H．首先求出OH、EC、BE，利用△BCE∽△BED，可得=，解决问题；【解答】解：（1）⊙O如图所示；（2）作OH⊥BC于H．∵AC是⊙O的切线，∴OE⊥AC，∴∠C=∠CEO=∠OHC=90°，∴四边形ECHO是矩形，∴OE=CH=，BH=BC﹣CH=，在Rt△OBH中，OH==2，∴EC=OH=2，BE==2，∵∠EBC=∠EBD，∠BED=∠C=90°，∴△BCE∽△BED，∴=，∴=，∴DE=．25．（2018•北京）下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程．已知：直线l及直线l外一点P．求作：直线PQ，使得PQ∥l．作法：如图，①在直线l上取一点A，作射线PA，以点A为圆心，AP长为半径画弧，交PA的延长线于点B；②在直线l上取一点C（不与点A重合），作射线BC，以点C为圆心，CB长为半径画弧，交BC的延长线于点Q；③作直线PQ．所以直线PQ就是所求作的直线．根据小东设计的尺规作图过程，（1）使用直尺和圆规，补全图形；（保留作图痕迹）（2）完成下面的证明．证明：∵AB=AP，CB=CQ，∴PQ∥l（三角形中位线定理）（填推理的依据）．【分析】（1）根据题目要求作出图形即可；（2）利用三角形中位线定理证明即可；【解答】（1）解：直线PQ如图所示；（2）证明：∵AB=AP，CB=CQ，∴PQ∥l（三角形中位线定理）．故答案为：AP，CQ，三角形中位线定理；26．（2018•白银）如图，在△ABC中，∠ABC=90°．（1）作∠ACB的平分线交AB边于点O，再以点O为圆心，OB的长为半径作⊙O；（要求：不写做法，保留作图痕迹）（2）判断（1）中AC与⊙O的位置关系，直接写出结果．【分析】（1）首先利用角平分线的作法得出CO，进而以点O为圆心，OB为半径作⊙O即可；（2）利用角平分线的性质以及直线与圆的位置关系进而求出即可．【解答】解：（1）如图所示：；（2）相切；过O点作OD⊥AC于D点，∵CO平分∠ACB，∴OB=OD，即d=r，∴⊙O与直线AC相切，27．（2018•无锡）如图，平面直角坐标系中，已知点B的坐标为（6，4）．（1）请用直尺（不带刻度）和圆规作一条直线AC，它与x轴和y轴的正半轴分别交于点A 和点C，且使∠ABC=90°，△ABC与△AOC的面积相等．（作图不必写作法，但要保留作图痕迹．）（2）问：（1）中这样的直线AC是否唯一？若唯一，请说明理由；若不唯一，请在图中画出所有这样的直线AC，并写出与之对应的函数表达式．【分析】（1）①作线段OB的垂直平分线AC，满足条件，②作矩形OA′BC′，直线A′C′，满足条件；（2）分两种情形分别求解即可解决问题；【解答】（1）解：如图△ABC即为所求；（2）解：这样的直线不唯一．①作线段OB的垂直平分线AC，满足条件，此时直线的解析式为y=﹣x+．②作矩形OA′BC′，直线A′C′，满足条件，此时直线A′C′的解析式为y=﹣x+4．28．（2018•孝感）如图，△ABC中，AB=AC，小聪同学利用直尺和圆规完成了如下操作：①作∠BAC的平分线AM交BC于点D；②作边AB的垂直平分线EF，EF与AM相交于点P；③连接PB，PC．请你观察图形解答下列问题：（1）线段PA，PB，PC之间的数量关系是PA=PB=PC；（2）若∠ABC=70°，求∠BPC的度数．【分析】（1）根据线段的垂直平分线的性质可得：PA=PB=PC；（2）根据等腰三角形的性质得：∠ABC=∠ACB=70°，由三角形的内角和得：∠BAC=180°﹣2×70°=40°，由角平分线定义得：∠BAD=∠CAD=20°，最后利用三角形外角的性质可得结论．【解答】解：（1）如图，PA=PB=PC，理由是：∵AB=AC，AM平分∠BAC，∴AD是BC的垂直平分线，∴PB=PC，∵EP是AB的垂直平分线，∴PA=PB，∴PA=PB=PC；故答案为：PA=PB=PC；（2）∵AB=AC，∴∠ABC=∠ACB=70°，∴∠BAC=180°﹣2×70°=40°，∵AM平分∠BAC，∴∠BAD=∠CAD=20°，∵PA=PB=PC，∴∠ABP=∠BAP=∠ACP=20°，∴∠BPC=∠ABP+∠BAC+∠ACP=20°+40°+20°=80°．29．（2018•深圳）已知菱形的一个角与三角形的一个角重合，然后它的对角顶点在这个重合角的对边上，这个菱形称为这个三角形的亲密菱形，如图，在△CFE中，CF=6，CE=12，∠FCE=45°，以点C为圆心，以任意长为半径作AD，再分别以点A和点D为圆心，大于AD 长为半径作弧，交EF于点B，AB∥CD．（1）求证：四边形ACDB为△FEC的亲密菱形；（2）求四边形ACDB的面积．【分析】（1）根据折叠和已知得出AC=CD，AB=DB，∠ACB=∠DCB，求出AC=AB，根据菱形的判定得出即可；（2）根据相似三角形的性质得出比例式，求出菱形的边长和高，根据菱形的面积公式求出即可．【解答】（1）证明：∵由已知得：AC=CD，AB=DB，由已知尺规作图痕迹得：BC是∠FCE的角平分线，∴∠ACB=∠DCB，又∵AB∥CD，∴∠ABC=∠DCB，∴∠ACB=∠ABC，∴AC=AB，又∵AC=CD，AB=DB，∴AC=CD=DB=BA∴四边形ACDB是菱形，∵∠ACD与△FCE中的∠FCE重合，它的对角∠ABD顶点在EF上，∴四边形ACDB为△FEC的亲密菱形；（2）解：设菱形ACDB的边长为x，∵四边形ABCD是菱形，∴AB∥CE，∴∠FAB=∠FCE，∠FBA=∠E，△EAB∽△FCE则：，即，解得：x=4，过A点作AH⊥CD于H点，∵在Rt△ACH中，∠ACH=45°，∴，∴四边形ACDB的面积为：．30．（2018•贵港）尺规作图（只保留作图痕迹，不要求写出作法）．如图，已知∠α和线段a，求作△ABC，使∠A=∠α，∠C=90°，AB=a．【分析】根据作一个角等于已知角，线段截取以及垂线的尺规作法即可求出答案．【解答】解：如图所示，△ABC为所求作31．（2018•江西）如图，在四边形ABCD中，AB∥CD，AB=2CD，E为AB的中点，请仅用无刻度直尺分别按下列要求画图（保留画图痕迹）．（1）在图1中，画出△ABD的BD边上的中线；（2）在图2中，若BA=BD，画出△ABD的AD边上的高．【分析】（1）连接EC，利用平行四边形的判定和性质解答即可；（2）连接EC，ED，FA，利用三角形重心的性质解答即可．【解答】解：（1）如图1所示，AF即为所求：（2）如图2所示，BH即为所求．32．（2018•青岛）已知：如图，∠ABC，射线BC上一点D．求作：等腰△PBD，使线段BD为等腰△PBD的底边，点P在∠ABC内部，且点P到∠ABC两边的距离相等．【分析】根据角平分线的性质、线段的垂直平分线的性质即可解决问题．【解答】解：∵点P在∠ABC的平分线上，∴点P到∠ABC两边的距离相等（角平分线上的点到角的两边距离相等），∵点P在线段BD的垂直平分线上，∴PB=PD（线段的垂直平分线上的点到线段的两个端点的距离相等），如图所示：33．（2018•宁波）在5×3的方格纸中，△ABC的三个顶点都在格点上．（1）在图1中画出线段BD，使BD∥AC，其中D是格点；（2）在图2中画出线段BE，使BE⊥AC，其中E是格点．【分析】（1）将线段AC沿着AB方向平移2个单位，即可得到线段BD；（2）利用2×3的长方形的对角线，即可得到线段BE⊥AC．【解答】解：（1）如图所示，线段BD即为所求；（2）如图所示，线段BE即为所求．34．（2018•河南）如图，反比例函数y=（x＞0）的图象过格点（网格线的交点）P．（1）求反比例函数的解析式；（2）在图中用直尺和2B铅笔画出两个矩形（不写画法），要求每个矩形均需满足下列两个条件：①四个顶点均在格点上，且其中两个顶点分别是点O，点P；②矩形的面积等于k的值．【分析】（1）将P点坐标代入y=，利用待定系数法即可求出反比例函数的解析式；（2）根据矩形满足的两个条件画出符合要求的两个矩形即可．【解答】解：（1）∵反比例函数y=（x＞0）的图象过格点P（2，2），∴k=2×2=4，∴反比例函数的解析式为y=；（2）如图所示：矩形OAPB、矩形OCDP即为所求作的图形．35．（2018•金华）如图，在6×6的网格中，每个小正方形的边长为1，点A在格点（小正方形的顶点）上．试在各网格中画出顶点在格点上，面积为6，且符合相应条件的图形．【分析】利用数形结合的思想解决问题即可；【解答】解：符合条件的图形如图所示：36．（2018•济宁）在一次数学活动课中，某数学小组探究求环形花坛（如图所示）面积的方法，现有以下工具；①卷尺；②直棒EF；③T型尺（CD所在的直线垂直平分线段AB）．（1）在图1中，请你画出用T形尺找大圆圆心的示意图（保留画图痕迹，不写画法）；（2）如图2，小华说：“我只用一根直棒和一个卷尺就可以求出环形花坛的面积，具体做法如下：将直棒放置到与小圆相切，用卷尺量出此时直棒与大圆两交点M，N之间的距离，就可求出环形花坛的面积”如果测得MN=10m，请你求出这个环形花坛的面积．【分析】（1）直线CD与C′D′的交点即为所求的点O．（2）设切点为C，连接OM，OC．旅游勾股定理即可解决问题；【解答】解：（1）如图点O即为所求；（2）设切点为C，连接OM，OC．∵MN是切线，∴OC⊥MN，∴CM=CN=5，∴OM2﹣OC2=CM2=25，=π•OM2﹣π•OC2=25π．∴S圆环37．（2018•广安）下面有4张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长都是1，请在方格纸中分别画出符合要求的图形，所画图形各顶点必须与方格纸中小正方形的顶点重合，具体要求如下：（1）画一个直角边长为4，面积为6的直角三角形．（2）画一个底边长为4，面积为8的等腰三角形．（3）画一个面积为5的等腰直角三角形．（4）画一个边长为2，面积为6的等腰三角形．【分析】（1）利用三角形面积求法以及直角三角形的性质画即可；（2）利用三角形面积求法以及等腰三角形的性质画出即可．（3）利用三角形面积求法以及等腰直角三角形的性质画出即可；（4）利用三角形面积求法以及等腰三角形的性质画出即可．【解答】解：（1）如图（1）所示：（2）如图（2）所示：（3）如图（3）所示；（4）如图（4）所示．38．（2018•青岛）问题提出：用若干相同的一个单位长度的细直木棒，按照如图1方式搭建一个长方体框架，探究所用木棒条数的规律．问题探究：我们先从简单的问题开始探究，从中找出解决问题的方法．探究一用若干木棒来搭建横长是m，纵长是n的矩形框架（m、n是正整数），需要木棒的条数．如图①，当m=1，n=1时，横放木棒为1×（1+1）条，纵放木棒为（1+1）×1条，共需4条；如图②，当m=2，n=1时，横放木棒为2×（1+1）条，纵放木棒为（2+1）×1条，共需7条；如图③，当m=2，n=2时，横放木棒为2×（2+1））条，纵放木棒为（2+1）×2条，共需12条；如图④，当m=3，n=1时，横放木棒为3×（1+1）条，纵放木棒为（3+1）×1条，共需10条；如图⑤，当m=3，n=2时，横放木棒为3×（2+1）条，纵放木棒为（3+1）×2条，共需17条．问题（一）：当m=4，n=2时，共需木棒22条．问题（二）：当矩形框架横长是m，纵长是n时，横放的木棒为m（n+1）条，纵放的木棒为n（m+1）条．探究二用若干木棒来搭建横长是m，纵长是n，高是s的长方体框架（m、n、s是正整数），需要木棒的条数．如图⑥，当m=3，n=2，s=1时，横放与纵放木棒之和为[3×（2+1）+（3+1）×2]×（1+1）=34条，竖放木棒为（3+1）×（2+1）×1=12条，共需46条；如图⑦，当m=3，n=2，s=2时，横放与纵放木棒之和为[3×（2+1）+（3+1）×2]×（2+1）=51条，竖放木棒为（3+1）×（2+1）×2=24条，共需75条；如图⑧，当m=3，n=2，s=3时，横放与纵放木棒之和为[3×（2+1）+（3+1）×2]×（3+1）=68条，竖放木棒为（3+1）×（2+1）×3=36条，共需104条．问题（三）：当长方体框架的横长是m，纵长是n，高是s时，横放与纵放木棒条数之和为[m（n+1）+n（m+1）]（s+1）条，竖放木棒条数为（m+1）（n+1）s条．实际应用：现在按探究二的搭建方式搭建一个纵长是2、高是4的长方体框架，总共使用了170条木棒，则这个长方体框架的横长是4．拓展应用：若按照如图2方式搭建一个底面边长是10，高是5的正三棱柱框架，需要木棒1320条．【分析】从特殊到一般探究规律后利用规律即可解决问题；【解答】解：问题（一）：当m=4，n=2时，横放木棒为4×（2+1）条，纵放木棒为（4+1）×2条，共需22条；问题（二）：当矩形框架横长是m，纵长是n时，横放的木棒为m（n+1）条，纵放的木棒为n（m+1）条；问题（三）：当长方体框架的横长是m，纵长是n，高是s时，横放与纵放木棒条数之和为[m （n+1）+n（m+1）]（s+1）条，竖放木棒条数为（m+1）（n+1）s条．实际应用：这个长方体框架的横长是s，则：[3m+2（m+1）]×5+（m+1）×3×4=170，解得m=4，拓展应用：若按照如图2方式搭建一个底面边长是10，高是5的正三棱柱框架，横放与纵放木棒条数之和为165×6=990条，竖放木棒条数为66×5=330条需要木棒1320条．故答案为22，m（n+1），n（m+1），[m（n+1）+n（m+1）]（s+1），（m+1）（n+1）s，4，1320；39．（2018•香坊区）如图，在每个小正方形的边长均为1的方格纸中，有线段AB和线段CD，点A、B、C、D均在小正方形的顶点上．（1）在方格纸中画出以AB为斜边的等腰直角三角形ABE，点E在小正方形的顶点上；（2）在方格纸中画出以CD为对角线的矩形CMDN（顶点字母按逆时针顺序），且面积为10，点M、N均在小正方形的顶点上；（3）连接ME，并直接写出EM的长．【分析】（1）利用等腰直角三角形的性质画出即可；（2）利用矩形的性质画出即可；（3）根据勾股定理解答即可．【解答】解：（1）如图所示；（2）如图所示；（3）如图所示，EM=40．（2018•天门）图①、图②都是由边长为1的小菱形构成的网格，每个小菱形的顶点称为格点．点O，M，N，A，B均在格点上，请仅用无刻度直尺在网格中完成下列画图．（1）在图①中，画出∠MON的平分线OP；（2）在图②中，画一个Rt△ABC，使点C在格点上．【分析】（1）构造全等三角形，利用全等三角形的性质即可解决问题；（2）利用菱形以及平行线的性质即可解决问题；【解答】解：（1）如图所示，射线OP即为所求．（2）如图所示，点C即为所求；41．（2018•哈尔滨）如图，方格纸中每个小正方形的边长均为1，线段AB的两个端点均在小正方形的顶点上．（1）在图中画出以线段AB为一边的矩形ABCD（不是正方形），且点C和点D均在小正方形的顶点上；（2）在图中画出以线段AB为一腰，底边长为2的等腰三角形ABE，点E在小正方形的顶点上，连接CE，请直接写出线段CE的长．【分析】（1）利用数形结合的思想解决问题即可；（2）利用数形结合的思想解决问题即可；【解答】解：（1）如图所示，矩形ABCD即为所求；（2）如图△ABE即为所求，CE=4．。

2018北京中考数学一模——16题尺规作图专题【2018东城一模】 16．已知正方形ABCD .求作：正方形ABCD 的外接圆. 作法：如图，（1）分别连接AC ，BD ，交于点O ;（2）以点O 为圆心，OA 长为半径作O .O 即为所求作的圆.请回答：该作图的依据是__________________________________.【2018西城一模】 16．阅读下面材料：在复习课上，围绕一道作图题，老师让同学们尝试应用学过的知识设计多种不同的作图方法，并交流其中蕴含的数学原理． 已知：直线和直线外的一点P ．求作：过点P 且与直线垂直的直线PQ ，垂足为点Q ． 某同学的作图步骤如下： 步骤 作法推断第一步 以点P 为圆心，适当长度为半径作弧，交直线于A ，B 两点．PA PB =第二步连接PA ，PB ，作APB ∠的平分线，交直线于点Q ．APQ ∠=∠__________直线PQ 即为所求作．PQ l ⊥请你根据该同学的作图方法完成以下推理: ∵PA PB =，APQ ∠=∠__________，∴PQ l ⊥．（依据：__________________________________________________）．【2018海淀一模】1．用三角板作△ABC 的边BC 上的高，下列三角板的摆放位置正确的是A B C DC BAA ABC ACAABCCBABCABCCB BC A B C【2018朝阳一模】16.下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程.已知：直线a和直线外一点P.求作：直线a的垂线，使它经过P.作法：如图，（1）在直线a上取一点A, 连接PA；（2）分别以点A和点P为圆心，大于AP的长为半径作弧，两弧相交于B，C两点，连接BC交PA于点D；（3）以点D为圆心，DP为半径作圆，交直线a于点E，作直线PE.所以直线PE就是所求作的垂线.请回答：该尺规作图的依据是．【2018石景山一模】16．小林在没有量角器和圆规的情况下，利用刻度尺和一副三角板画出了一个角的平分线，他的做法是这样的：如图，（1）利用刻度尺在AOB=；∠的两边OA，OB上分别取OM ON（2）利用两个三角板，分别过点M，N画OM，ON的垂线，交点为P；（3）画射线OP．则射线OP为AOB∠的平分线．请写出小林的画法的依据．【2018门头沟一模】16. 下图是“已知一条直角边和斜边做直角三角形”的尺规作图过程．已知：线段a 、b ，求作：Rt ABC ∆．使得斜边AB b =,AC a = 作法：如图．（1）作射线AP ，截取线段AB b =； （2）以AB 为直径，作⊙O ；（3）以点A 为圆心，a 的长为半径作弧交⊙O 于点C ； （4）连接AC 、CB .ABC ∆即为所求作的直角三角形．请回答：该尺规作图的依据是______________________________________．【2018大兴一模】16．下面是“求作∠AOB 的角平分线”的尺规作图过程．已知：如图，钝角∠AOB. 求作：∠AOB 的角平分线. 作法：①在OA 和OB 上，分别截取OD 、OE ，使OD ＝OE ； ②分别以D 、E 为圆心，大于12DE 的长为半径作 弧, 在∠AOB 内，两弧交于点C ； ③作射线OC.所以射线OC 就是所求作的∠AOB 的角平分线.请回答：该尺规作图的依据是 ． abPCOAB【2018顺义一模】16．在数学课上，老师提出一个问题“用直尺和圆规作一个矩形”．小华的做法如下： 老师说：“小华的作法正确” ．请回答：小华的作图依据是 ．【2018平谷一模】16．下面是“作已知角的角平分线”的尺规作图过程．已知：如图1，∠MON ．求作：射线OP ，使它平分∠MON ． 作法：如图2，（1）以点O 为圆心，任意长为半径作弧，交OM 于点A ，交ON 于点B ； （2）连结AB ；（3）分别以点A ，B 为圆心，大于12AB 的长为半径作弧，两弧相交于点P ；ONM图1图2PB ONMA（1）如图1，任取一点O ，过点O 作直线l 1，l 2；（2）如图2，以O 为圆心，任意长为半径作圆，与直线l 1，l 2分别相交于点A 、C ，B 、D ；（3）如图3，连接AB 、BC 、CD 、DA ．四边形ABCD 即为所求作的矩形．图3图2图1OOOABCDl 1l 2l 1l 2l 2l 1DCBA（4）作射线OP ．所以，射线OP 即为所求作的射线．请回答：该尺规作图的依据是 ． 【2018怀柔一模】 16.阅读下面材料：在数学课上，老师提出利用尺规作图完成下面问题：小明的作法如下：请回答：该尺规作图的依据是____________________________.【2018延庆一模】1． 利用尺规作图，作△ABC 边上的高AD ，正确的是【2018延庆一模】20．已知：∠AOB 及边OB 上一点C ．求作：∠OCD ，使得∠OCD=∠AOB ．要求：1．尺规作图，保留作图痕迹，不写做法；（说明：作出一个．．即可） 2．请你写出作图的依据．ABCDABC DABC DABCDA ．B ． 已知：△ABC.求作：△ABC 的内切圆.BAC如图,(1)作∠ABC ，∠ACB 的平分线BE 和CF ，两线相交于点O;(2)过点O 作OD ⊥BC ，垂足为点D; (3)点O 为圆心，OD 长为半径作⊙O. 所以，⊙O 即为所求作的圆.DOCA BEF【2018燕山一模】16．在数学课上，老师提出如下问题：曈曈的作法如下：老师说：“曈曈的作法正确．”请你回答：曈曈的作图依据是________________________．。

2018中考数学试题分类汇编：考点32 尺规作图一．选择题（共13小题）1．（2018?襄阳）如图，在△ABC中，分别以点A和点C为圆心，大于AC长为半径画弧，两弧相交于点M，N，作直线MN分别交BC，AC于点D，E．若AE=3cm，△ABD的周长为13cm，则△ABC的周长为（）A．16cm B．19cm C．22cm D．25cm【分析】利用线段的垂直平分线的性质即可解决问题．【解答】解：∵DE垂直平分线段AC，∴DA=DC，AE=EC=6cm，∵AB+AD+BD=13cm，∴AB+BD+DC=13cm，，∴△ABC的周长=AB+BD+BC+AC=13+6=19cm故选：B．2．（2018?河北）尺规作图要求：Ⅰ、过直线外一点作这条直线的垂线；Ⅱ、作线段的垂直平分线；Ⅲ、过直线上一点作这条直线的垂线；Ⅳ、作角的平分线．如图是按上述要求排乱顺序的尺规作图：则正确的配对是（）A．①﹣Ⅳ，②﹣Ⅱ，③﹣Ⅰ，④﹣ⅢB．①﹣Ⅳ，②﹣Ⅲ，③﹣Ⅱ，④﹣ⅠC．①﹣Ⅱ，②﹣Ⅳ，③﹣Ⅲ，④﹣ⅠD．①﹣Ⅳ，②﹣Ⅰ，③﹣Ⅱ，④﹣Ⅲ【分析】分别利用过直线外一点作这条直线的垂线作法以及线段垂直平分线的作法和过直线上一点作这条直线的垂线、角平分线的作法分别得出符合题意的答案．【解答】解：Ⅰ、过直线外一点作这条直线的垂线；Ⅱ、作线段的垂直平分线；Ⅲ、过直线上一点作这条直线的垂线；Ⅳ、作角的平分线．如图是按上述要求排乱顺序的尺规作图：则正确的配对是：①﹣Ⅳ，②﹣Ⅰ，③﹣Ⅱ，④﹣Ⅲ．故选：D．3．（2018?河南）如图，已知?AOBC的顶点O（0，0），A（﹣1，2），点B在x轴正半轴上按以下步骤作图：①以点O为圆心，适当长度为半径作弧，分别交边OA，OB于点D，E；②分别以点D，E为圆心，大于DE的长为半径作弧，两弧在∠AOB内交于点F；③作射线OF，交边AC于点G，则点G的坐标为（）A．（﹣1，2）B．（，2）C．（3﹣，2）D．（﹣2，2）【分析】依据勾股定理即可得到Rt△AOH中，AO=，依据∠AGO=∠AOG，即可得到AG=AO=，进而得出HG=﹣1，可得G（﹣1，2）．【解答】解：∵?AOBC的顶点O（0，0），A（﹣1，2），∴AH=1，HO=2，∴Rt△AOH中，AO=，由题可得，OF平分∠AOB，∴∠AOG=∠EOG，。

专题五尺规作图考情分析尺规作图每年必考，除2017年在解答题(二)第1题出现外，其余年份均在解答题(一)第3题考查；2017年分值为7分，2013年分值为5分，其余年份均为6分．考查了作线段的垂直平分线、过一点作已知线段的垂线、作已知角的平分线、作一条线段等于已知线段等．涉及三角形的内角和、全等、中位线、外角性质、角平分线的性质、平行线的判定等．预计18年仍将作为解答题出现．例如图1，△ABC是等腰直角三角形，∠C＝90°.(1)作∠B的平分线BD交AC于点D；(用尺规作图，保留作图痕迹，不要求写作法)(2)若CD＝3，求点D到AB的距离．图1训练 1.如图2所示，在Rt△ABC中，∠C＝90°，∠B＝60°，AC＝1.图2(1)尺规作图：在线段AB的延长线上作线段BD，使得BD＝BC；(保留作图痕迹，不要求写作法)(2)在已作的图形中，连接CD，求CD的长．2．如图3，在△ABC中，∠C＝90°，∠A＝30°.图3(1)用尺规作图作AB边上的垂直平分线DE，交AC于点D，交AB于点E；(保留作图痕迹，不要求写作法)(2)连接BD，求证：DE＝D C.3．如图4，在平行四边形ABCD中，AB＜B C.图4(1)利用尺规作图，在BC边上确定点E，使点E到边AB，AD的距离相等；(保留作图痕迹，不要求写作法)(2)若BC＝8，CD＝5，则CE＝__________.4．如图5，点A，C分别在∠XOY的边OX和OY上，图5(1)尺规作图：在OY的右侧作∠Y CP＝∠YO A；(保留作图痕迹，不要求写作法)(2)在射线CP上取一点B，使CB＝O A，连接AB，问：四边形O ABC是什么四边形？5．如图6，在△ABC中：图6(1)请你作出AC边上的高BD；(用尺规作图，保留作图痕迹，不要求写作法)(2)若AB＝AC＝8，BC＝6，求B D.6．如图7，已知△AB C.图7(1)请用尺规作△ABC的中位线DE，其中点D，E分别在AB，AC上；(保留作图痕迹，不要求写作法)(2)延长DE至点F，使得EF＝DE，求证：四边形DBCF是平行四边形．7．如图8、图9所示，已知：线段a，b和∠α.图8 图9(1)用尺规作△ABC，使BC＝a，AC＝b，∠C＝∠α；(保留作图痕迹，不要求写作法)(2)若∠C＝30°，a＝10，b＝6，求△ABC的面积．参考答案例解：(1)如图1所示；(2)如图1，过点D作DE⊥AB于点E，∵∠C＝90°，BD是∠ABC的平分线，∴DE＝DC＝3.图1训练 1.解：(1)如图2，线段BD即为所求；图2(2)∵BD＝BC，∴∠BCD＝∠BDC.∵∠ABC＝60°，∴∠BDC＝30°.∵∠ACB＝90°，∠ABC＝60°，∴∠A＝30°.∴∠BDC＝∠A.∴CD＝AC＝1.2．(1)解：如图3，DE即为所求；(2)证明：∵DE垂直平分AB，∴DA＝DB.∴∠DBA＝∠A＝30°.∵∠ABC＝90°－∠A＝60°，∴∠CBD＝30°，即BD平分∠ABC.∵DE⊥AB，DC⊥BC，∴DE＝DC.图33．解：(1)如图4所示，E点即为所求．图4(2)3.理由：∵四边形ABCD是平行四边形，∴AB＝CD＝5，AD∥BC.∴∠DAE＝∠AEB.∵AE 是∠A 的平分线，∴∠DAE ＝∠BAE .∴∠BAE ＝∠BEA .∴BE ＝BA ＝5.∴CE ＝BC －BE ＝3. 4．解：(1)如图5所示．图5(2)四边形OABC 是平行四边形，理由如下：∵∠YCP ＝∠YOA ，∴CB ∥OA . ∵CB ＝OA ，∴四边形OABC 是平行四边形． 5．解：(1)如图6所示，BD 即为所求．图6(2)设AD ＝x ，则CD ＝8－x ，∵BD ⊥AC ，∴Rt △ABD 中，BD 2＝AB 2－AD 2＝82－x 2， Rt △BCD 中，BD 2＝BC 2－CD 2＝62－(8－x )2. ∴82－x 2＝62－(8－x )2，解得x ＝234.∴Rt △ABD 中，BD ＝AB 2－AD 2＝82－⎝⎛⎭⎫2342＝34 55.6．(1)解：如图7，线段DE 即为所求；图7(2)证明：∵DE 是△ABC 的中位线，∴BC ＝2DE ，且BC ∥DE . ∵EF ＝DE ，∴DF ＝2DE .∴BC ＝DF . ∴四边形DBCF 是平行四边形．7．解：(1)如图8所示，△ABC 即为所求；图8(2)如图9，作AD ⊥BC 于D ，图9∵∠α＝30°，a ＝10，b ＝6， ∴Rt △ACD 中，AD ＝12AC ＝3.∴S △ABC ＝12×10×3＝15.。

2018一模尺规作图汇编例题作一个角等于已知角例题1、（18番禺）如图，四边形ABCD是平行四边形，把△ABD沿对角线BD翻折180°得到△A′BD．（1）利用尺规作出△A′BD．（要求保留作图痕迹，不写作法）；（2）设DA′与BC交于点E，求证：△BA′E≌△DCE．作角平分线例题2、（18二中）如图，在Rt△ABC中∠A=90°，AC=4.（1）利用尺规作∠ABC的平分线交AC于点D;（保留作图痕迹，不写作法）=y2－1y2－2y＋1÷（1y－1－1y＋1），作垂直平分线例题3、（18四中、聚贤）如图，AC 是平行四边形ABCD 的对角线． （1）利用尺规作出AC 的垂直平分线（要求保留作图痕迹，不写作法）；（2）设AC 的垂直平分线分别与AB ，AC ，CD 交于点E ，O ，F ，求证：以A ，E ，C ，F 为顶点的四边形为菱形．例题4、（18一中）如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A ，B ，C ． （1）请完成如下操作：①以点O 为原点、竖直和水平方向所在的直线为坐标轴、网格边长为单位长，建立平面直角坐标系； ②用直尺和圆规画出该圆弧所在圆的圆心D 的位置（不用写作法，保留作图痕迹），并连接AD ，CD ．（2）请在（1）的基础上，完成下列问题： ①写出点的坐标：C _______，D _______； ②⊙D 的半径＝________（结果保留根号）； ③若点E （7，0），试判断直线EC 与⊙D 的位置关系，并说明你的理由．例题5、（18省实、培正、广州中学）如图，等腰三角形ABC 中，AC ＝BC ＝10，AB ＝12.（1）动手操作：利用尺规作以BC 为直径的⊙O ，⊙O 交AB 于点D ，⊙O 交AC 于点E ，并且过点D 作DF ⊥AC 交AC 于点F ．（2）求证：直线DF 是⊙O 的切线；（3）连接DE ，记△ADE 的面积为S 1，四边形DECB 的面积为S 2，求S 1S 2的值．课堂训练1、（18三中）如图，利用尺规，在△ABC的边上方作∠CAB＝∠ACB，在射线AE上截取AD＝BC，连接CD，并证明：CD∥AB（尺规作图要求保留作图痕迹，不写作法）2、（18花都）如图，⊙O是△ABC的外接圆．（1）尺规作图：作出∠C的角平分线CD，与⊙O交于点D，与AB交于点E；（不写作法，保留作图痕迹）（2）在（1）的条件下，连接BD．①求证：△BDE∽△CDB②若BD＝7，DE·EC＝3，求DE的长．3、（18南沙）如图，在ΔABC中，AC=BC，∠ACB=90゜, ∠ACD为ΔABC的一个外角.(1) 请根据要求进行尺规作图，并在图中标明相应字母.（保留作图痕迹，不写做法）①作∠ACD的平分线CM；②做线段AC的垂直平分线，与CM交于点F，与AB边交于点E，连接AF，CE .(2) 判断四边形AECF的形状并加以证明.4、（18荔湾）如图，AC是矩形ABCD的一条对角线.（1）作AC的垂直平分线EF，分别交AB、DC于点E、F，垂足为O；（要求用尺规作图，保留作图痕迹，不要求写做法）（2）求证：OE=OF5、（18越秀外国语）如图，在△ABC，∠C＝90°，（1）请用尺规按下列顺序作图，保留作图痕迹①作线段AB垂直平分线m，交BA于点D，交CA于点E．②连接BE；（2）若BC＝6，AC＝8，求tan∠CBE．6、（18三中）如图，在△ABC中，AB＝AC，D是BA延长线上的一点，点E是AC的中点.（1）实践与操作：利用尺规按下列要求作图，并在图中标明相应字母（保留作图痕迹，不写作法）.○1作∠DAC的平分线AM. ○2连结BE并延长交AM于点F.（2）猜想与证明：试猜想AF与BC有怎样的位置关系和数量关系，并说明理由.课后作业1、（18真光一模）已知，如图，在Rt△ABC中，∠C＝90°，∠BAC的角平分线AD交BC边于2、（18增城一模）如图所示，在Rt△ABC中，∠C＝90°，AD是∠BAC的角平分线，以AB上一点O为圆心，AD为弦作⊙O.（1）尺规作图：作出⊙O，并连接OD（不写作法与证明，保留作图痕迹）；（2）求证：△OBD∽△ABC.3、（18越秀外国语）如图，在△ABC，∠C＝90°，（1）请用尺规按下列顺序作图，保留作图痕迹①作线段AB垂直平分线m，交BA于点D，交CA于点E．②连接BE；（2）若BC＝6，AC＝8，求tan∠CBE．4、（18育才）已知∠ABC及角内一点P．（1）求作：用尺规作图，作∠ABC的平分线BK（保留作图痕迹，不写作法）；（2）请你在∠ABC的平分线BK上找到点M，使点M到∠ABC的两边的距离等于MP，并说明理由．5、（18汇景）如图，在△ABC 中，∠A ＝30°，∠B ＝60°.（1）作∠B 的平分线BD 交AC 于点D （要求用尺规作图，不写作法，保留作图痕迹）； （2）若S △BDC ＝a ，S △BDA ＝b ，求ab的值.6、（18华侨）如图,在Rt △ABC 中,∠C =90°.AD 是∠BAC 的角平分线,以AB 上一点O 为圆心,AD 为弦作⊙0(1)在图中作出⊙o （不写作法,保留作图痕迹）(2)求证:BC 为0的切线(2) AC =3,tan α＝34求⊙o 的半径长7、（18广雅）如图，Rt △ABC 中，∠C ＝90°，AC ＝8，BC ＝6．（1）尺规作图：作△BAC 的平分线AD （保留作图痕迹，不写作法）； （2）求AD 的长．8、（18广大附中）如图，在△ABC 中，∠ABC ＝80°，∠BAC ＝40°，AB 的垂直平分线分别与AC ，AB 交于点D ，E ．（1）用圆规和直尺在图中作出AB 的垂直平分线DE ，并连接BD ； （2）证明：△ABC ∽△BDC ．9、（18，16中）在△ABF 中，C 为AF 上一点且AB ＝AC .（1）尺规作图：作出以AB 为直径的⊙O ，⊙O 分别交AC ，BC 于点D ，E ，在图上标出D ，E ，在图上标出D ，E （保留作图痕迹，不写作法）．（2）若∠BAF ＝2∠CBF ，求证：直线BF 是⊙O 的切线； （3）在（2）中，若AB ＝5，55sin ∠CBF=，求BC 和BF 的长．10、（18白云）如图10，AD是Rt△ABC斜边BC上的高.（1）尺规作图：作∠C的平分线，交AB于点E，交AD于点F（不写作法，必须保留作图痕迹，标上应有的字母）；（2）在（1）的条件下，过F画BC的平行线交AC于点H，线段FH与线段CH的数量关系如何？请予以证明；（3）在（2）的条件下，连结DE、DH.求证：ED⊥HD.。