当前位置：文档之家 › 弹塑性力学应力函数解法详细讲解

弹塑性力学应力函数解法详细讲解

  • 格式：ppt
  • 大小：572.00 KB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

弹塑性力学应力函数解法详细讲解

弹塑性力学应力函数解法详细讲解

1 x y E 1 y y x E 21 代入到本构方程 xy xy E
x
x xy fx 0 x y xy x y y fy 0


f f 2 x y x y
V x V F y y F x
式子中的V为体力势函数。 同样可以引进一个airy函数，使得他满足下面的 关系式 2 x V 2
y
此时微分方程自动满足
y
xy
2 V x 2 2 xy
Company Logo
弹塑性平面问题的应力函数解法

相容方程可简化为
( x y ) 0
2
引进函数 ，使得它 满足如下的关系式
x, y
2 2 4 0 4 x x y y
4 4 4
x 2 / y 2 y 2 / x 2 xy 2 / xy
其中是拉普拉 斯算子
2 2 2 x 2 y 2 z 2
• 将airy函数代入平衡微 分方程，则平衡方程 自动满足，代入应变 协调方程 得到
上式可简化为
0
4 2 2
弹塑性平面问题的应力函数解法
2. 体力为有势的情况 即 代入平面微分方程化为
( x V ) xy 0 x y xy ( y V ) 0 x y
Z
将上式 代入本构方程得平 面 方程
应力问题中的物理方程即
1 x y E 1 y y x E
应变问题中的物理
x
1 xy G E 其中G 21
xy
1 2 x ( x y) E 1 1 2 y ( y x) E 1 21 xy xy E z xz yz 0

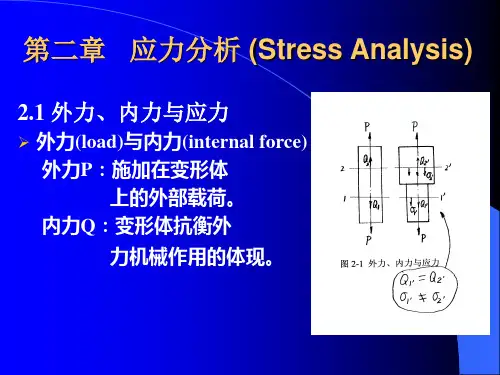
2-弹塑性力学-应力分析

2-弹塑性力学-应力分析
正应力 剪应力
1 1 3 3 1 τ8 = (σ1 σ 2 )2 + (σ 2 σ 3 )2 + (σ 3 σ1 )2 3
σ 8 = (σ1 + σ 2 + σ 3 ) = I1
总应力
2 2 P = σ8 +τ8 8
八面体上的正应力与塑性变形无关,剪应力与塑性变形有关. 八面体上的正应力与塑性变形无关,剪应力与塑性变形有关.
不计体力) (不计体力)
物理意义:表示变形体内无限相邻两质点的点的应力状态的关系. 物理意义:表示变形体内无限相邻两质点的点的应力状态的关系. 对弹性变形和塑性变形均适用. 对弹性变形和塑性变形均适用.
第二章 应力分析 (Stress Analysis)
推导原理:
– 静力平衡条件: 静力平衡条件: –
σ I1σ + I2σ I3 = 0
3 2
(σ3 I1σ2 I2σ I3 = 0)
(σ σ1)(σ σ2)(σ σ3) = 0
第二章 应力分析 (Stress Analysis)
应力不变量
式中
I1 = σ x + σ y + σ z = σ 1 + σ 2 + σ 3
σx I2 = τ yx
τ xy σ y + σ y τ zy
r r r Sn = σ n + τ n r r r r σn = σ x +σ y +σ z r r r r τn = τ x +τ y +τ z
或者
σ = σ l l ij i j n S n = σ ij l i 2 2 τ n = S n σ n
(求和约定的缩写形式) 求和约定的缩写形式) 应力平衡微分方程

3.9 应力函数解法

3.9 应力函数解法
应力函数法既保留了应力解法的优点能直接求解应力分量又吸收了位移解法的思想能自动满足平衡方程基本未知量降为3个所以是弹性理论中最常用的解法之一
使用教材：《材料固体力学》上册 周益春编著 科学出版社
应力函数解法
应力函数的引出： 应变 6 个分量可由协调方程约束后，化为独立的 3 个分量，相当于 3 个位移（单 值连续）； 应力 6 个分量可由平衡方程约束后，也可独立出 3 个分量，它也一定存在类似位 移的事先满足平衡方程的量。下面来寻找这个量：
(**)
=
Φ ,=
Φ, +
Φ,
+
Φ, +
Φ,
+
Φ, +
Φ,
= −Φ , + Φ , + Φ , = − , + , + , = − , + , + , ,
Email: onexf@
使用教材：《材料固体力学》上册 周益春编著 科学出版社
对于二维平面弹性问题，可进一步简化。若选 1 个Φ 分量作为应力函数： 若令 Maxwell 量为： = = 0； = Φ( , ) 这就是平面问题中的 G.B. Airy 应力函数（最早的应力函数）。 若令 Morera 量为： = Φ( , )； = = 0 这就是柱形杆扭转问题中的 Prandtl 应力函数
=
,
(其中：Φ = Φ )
(2)
ΦΦΦ
[Φ] =
ΦΦ
Φ
场函数 称为 Beltrami 应力函数张量，它自动满足平衡方程。 将(2)式代入常体力的 B-M 方程（3 个）来求解，得：
∇
,+
, , =0
(3)
Email: onexf@

弹塑性力学——应力

弹塑性力学——应力

x xy xz yx y yz z zx zy
• 张量表示 用1、2、3取代下标x、y、z，
11 12 13 ij 21 22 23 31 32 33
• 应力正、负号规定 正面上的应力若指向坐标轴正方向为正，否则为负； 负面的应力若指向坐标轴负方向为正，否则为负。
y
应力分量的坐标变换
• 新旧坐标的夹角 ex
e ' x
ey
m1 m2
ez
n1 n2
l1 l2
ey '
ez'
l3
m3
n3
• e ' 面（斜截面）的应力矢量在旧坐标下的分量 x
Tx＝xl1+yxm1+zxn1 Ty＝xyl1+ym1+zyn1 Tz＝xzl1+yzm1+zn1
• 力矩平衡：绕z轴
(xydydz)dx(yxdxdz)dy=0 xy＝yx 绕x和y方向的形心轴取矩 yz=zy xz= zx
静力学边界条件
n X A
xl+yxm+zxn＝ X
xyl+ym+zyn＝ Y ＝
xzl+yzm+zn
Z
z y x
例1-2 如图所示的楔形体受水压力作用，水的容重为，试写出边界条 件。
zx zx dz dxdy zx dxdy Xdxdydz 0 z
x yx zx X 0 x y z
• 由y、z方向的平衡
xy x y y zy z Y 0
xz yz z Z 0 x y z

弹塑性力学应力分析

弹塑性力学应力分析

解之 将 联立
代入
解之
将 联立
代入
解之
将 联立
代入
解之
二. 最大和最小应力
3 z
3
设一点的主应力及其主方向已知，现以 三主方向取Oxyz坐标，如图所示 设任一斜截面N，其方向余弦为l1、l2、l3 2
则由斜截面正应力公式 及
1x
N
12
N
O
y2
1
主应力单元体
3
求极值
解之 同理，将
xxyy ( x 12))22 x2x2yy
xxyy ( y 12))22 x2x2yy
ll33((21) 0
设 为第一主方向与x轴的夹角
则由三角函数关系可得
例2-2 已知弹性体内部某点的 应力状态为
a 0 a
ij
0
a
0
a 0
a 0 a
求主应力和主方向。
解：不变量的计算
代入特征方程
C zx pz
yx
xy
xz
x
zy yz
N
pN y
设斜截面上全应力为：
O y
yz
x
zy
xz xy zx
yzp y
B
y
沿坐标的分量为：
px
A
z
x
简写为：
设四面体斜面的面积为：
则三个直面的面积为：
简写为：
考虑四面体微元的平衡
X 0 Y 0
pxdSN xdSx yxdSy zxdSz 0 pydSN xydSx ydSy zydSz 0
将 向外法线和斜面分解为 和 。
则
即
将Cauchy定理代入：
展开整理得：

弹塑性力学讲义应力

弹塑性力学讲义应力

第1章 应 力1. 1 应力矢量物体受外力作用后，其内部将产生内力，即物体本身不同部分之间相互作用的力。

为了描述内力场，Chauchy 引进了应力的重要概念。

对于处于平衡状态的物体，假想使用一个过P 点的平面C 将其截开成A 和B 两部分。

如将B 部分移去，则B 对A 的作用应以分布的内力代替。

考察平面C 上包括P 点在内的微小面积，如图1.1所示。

设微面外法线（平面C 的外法线）为n ，微面面积为∆S ，作用在微面上的内力合力为∆F ，则该微面上的平均内力集度为∆F /∆S ，于是，P 点的内力集度可使用应力矢量T (n )，定义为T (n ) =SFs ∆∆∆0lim→B∆SACPn ∆Fxyz图1.1 应力矢量定义在笛卡儿坐标系下，使用e x ，e y 和e z 表示坐标轴的单位基矢量，应力矢量可以表示为T (n ) = T x e x +T y e y +T z e z（1.1）式中T x 、T y 和T z 是应力矢量沿坐标轴的分量。

上篇弹性力学第1章应力8除进行公式推导外，通常很少使用应力矢量的坐标分量T x、T y 和T z。

实际应用中，往往需要知道应力矢量沿微面法线方向和切线方向的分量，沿法线方向的应力分量称为正应力，沿切线方向的应力分量称为剪应力。

显而易见，应力矢量的大小和方向不仅取决于P点的空间位置，而且还与所取截面的法线方向n有关，即作用在同一点不同法线方向微面上的应力矢量不同。

所有这些应力矢量构成该点的应力状态。

由应力矢量的定义并结合作用力与反作用力定律，在同一点，外法线为-n微面上的应力矢量为：T(-n)= -T(n) （1.2）1.2 应力张量人们讨论问题常常是在笛卡儿坐标中进行，因此，我们使用六个与坐标面平行的平面从图1.1中P点的邻域截取一个微六面体，如图1.2所示。

在这个微六面体中，若微面的外法线方向与坐标正方向一致，则称为正面；若与坐标正方向相反，则称为负面。

弹塑性力学课件

弹塑性力学课件
应力分析 应变分析 应力应变关系
.
第三讲：应力应变分析
. 弹塑性力学研究生核心课程 任晓丹
同济大学建筑工程系
October 10, 2016
任晓丹
第三讲：应力应变分析
应力分析 应变分析 应力应变关系
EulerCauchy 应力原理
Ti
( n)
= lim
∆Fi dFi = ∆s→0 ∆S dS
任晓丹
任晓丹 第三讲：应力应变分析
σij − σδij = 0
应力分析 应变分析 应力应变关系
应力偏量
定义静水应力： 1 1 1 σm = Tr(σ ) = σii = (σ1 + σ2 + σ3 ) 3 3 3 应力偏量定义为： sij = σij − σm δij 应力偏量表示纯剪应力状态，对于很多材料，是其重要的破 坏控制机制，所以应力偏量应用十分广泛。 J1 、J2 和 J3 分别称为应力偏张量的第一、第二、第三不变 量。由于 J1 = 0，因此，一点的应力状态也可以用 I1 、J2 和 J3 表示。
任晓丹
第三讲：应力应变分析
应力分析 应变分析 应力应变关系
（第二）平衡方程
合力矩为零 ∫ MO = ∫∂ Ω =
∂Ω
∫ r × TdS + ϵijk xj Tn k dS +
Ω
∫
r × FdΩ ϵijk xj Fk dΩ = 0
Ω
第一项 ∫ R1 =
∂Ω
∫ ϵijk xj σmk nm dS =
Ω
′ ′ βki tk = σij nl βlj ⇒ βmi βki tk = δmk tk = tm = βmi σij nl βlj
应力转轴公式 (张量表达)

弹塑性力学弹性与塑性应力应变关系详解课件

弹塑性力学弹性与塑性应力应变关系详解课件

有限差分法
有限差分法（Finite Difference Method，简称FDM）是一种基于差分原 理的数值模拟方法。
它通过将连续的时间和空间离散化为有限个差分节点，并利用差分近似代 替微分方程中的导数项，从而将微分方程转化为差分方程进行求解。
有限差分法适用于求解偏微分方程，尤其在求解波动问题和热传导问题方 面具有优势。
05
弹塑性力学的数值模拟方法
有限元法
有限元法（Finite Element Method，简称 FEM）是一种广泛应用于解决复杂工程问题 的数值模拟方法。
它通过将连续的求解域离散化为有限个小的 单元，并对每个单元进行数学建模，从而将 复杂的连续场问题转化为离散的有限元问题。
有限元法具有灵活性和通用性，可以处理各 种复杂的几何形状和边界条件，广泛应用于 结构分析、热传导、流体动力学等领域。
与应变之间不再是线性关系。
重要性
03
了解塑性应力应变关系对于工程设计和结构安全评估具有重要
意义。
屈服准 则
屈服准则定义
描述材料开始进入塑性变形 阶段的条件。
常用屈服准则
例如，Von Mises屈服准则、 Tresca屈服准则等。
屈服准则的意义
为判断材料是否进入塑性变 形阶段提供依据，是弹塑性 力学中的重要概念。
弹塑性力学弹性与塑性应 力应变关系详解课件
目录
• 弹性应力应变关系 • 塑性应力应变关系 • 弹塑性本构模型 • 弹塑性力学的数值模拟方法
01
弹塑性力学基 础
弹塑性力学定义
01
02
03
弹塑性力学
是一门研究材料在弹性与 塑性范围内应力应变关系 的学科。
弹性
材料在受到外力作用后能 够恢复到原始状态的性质。

弹塑性力学讲义 第四章应力应变关系

弹塑性力学讲义 第四章应力应变关系

A 中有体积分和面积分，利用柯西公式和散度定理将面积分换成
体积分。
S Fiui dS S ( ijui )n j dS V ( jiui ), j dV
上式代入外力功增量
A ( fi ji, j )ui dV jiui, j dV ijijdV WdVU
弹性主轴
x3 为弹性主轴或材料主轴， 并取另一坐标系 x’i
， 且 x’1
= x1， x’2=x2， x’3=-x3。
4
在两个坐标下，弹性关系保持不变，则[C]中元素减少为 13 个独立系数。
Qi’j
x’1 = x1 x’2=x2 x’3=-x3
代入
x1
1 0 0 1
x2
0 0 0 -1
x3
0
i ' j ' Qi ' k Q j 'l kl
2
i ' j ' Qi ' k Q j 'l kl
得
x ' x1 ， x ' x 2
1
3 1
，
x ' x3
3
，
x ' x ' x1 x 2
1 2
x ' x ' x3 x1 ， x ' x ' x3 x 2
3 2
应变分量具有相同关系式。
[C]
为对称矩阵
[C]= [C]T。
最后 Eijkl 的独立系数为 21 个——材料为各向异性线弹性材料。 *对各向异性材料的本构关系可见，剪应变引起正应力，正应变也产生 剪应力。 弹性材料性质一般都具有某些对称性，利用对称可简化 [C] 中系数。 2.2 具有一个弹性对称面的材料 若物体内各点都有这样一个平面， 对此平面对称方向其弹性性质相同，则 称此平面为弹性对称面，垂直弹性对称面 的方向称为弹性主轴。 如取弹性对称面为 x1 —x2 面， x1 x3’ x2 x3

弹塑性力学第三章 应力与应变讲解

弹塑性力学第三章 应力与应变讲解

?
2?
zx
l3l1
?? ?
?n ?
p2
?
?
2 n
?
（3.10)
??
其中第2式 ? n ? pili ? ? ijlil j
(3.11)
8 应力分量的坐标变换规律
应力张量是一个二阶张量，因此，在数学上，应力张量 的各分量在坐标变换时，要服从二阶张量的坐标变换规 律。容易证明，如果坐标系仅作平移变换，则同一点的 各应力分量是不会发生变化的；只有在坐标系作旋转变 换时，同一点的各应力分量才会改变。下面证明给出坐 标旋转时应力张量所服从的规律。
同理可以写出其它应力分量，经整理后可简写为
? i ' j ' ? li 'il j ' j? ij
(3.13)
上式就是应力张量各分量在坐标旋转变换时所服从的变换 规律，它恰好符合二阶张量定义，剪应力互等表明它是对 称张量。
3.2 主应力与主应力空间
3.2.1 主应力和主方向
在受力物体内一点任意方向的微分面上，一般都有正应力 分量和剪应力分量存在。由应力张量的坐标变换规律知，当 通过同一点的微分面发生转动时，其法线也发生改变，相应 的正应力和剪应力数值也会变化。在微分面的不断转动过程 中，将会出现这样的微分面，在该面上只有正应力而剪应力 为零。只有正应力而没有剪应力的平面称 为主平面，其法线 方向称为应力主方向，简称主方向，其上的正应力称为主应 力。 根据主平面的定义，若设n为过物体内任意一点M的主平面 的单位法向量，它与三个坐标轴之间的夹角余弦为 l1、l2、l3
? X?0
1
px? S ? ? x (? S ?l1) ? ? yx (? S 以上方程两边同时除以

弹塑性力学-01应力分析

弹塑性力学-01应力分析

A x
pv2px 2p2 ypz2
l2
1 2m 2 2 2n2
2 3
2 v
pv2
2 v
l2 1 2 m 2 2 2 n 2 3 2v 232
3、应力圆
123
v l21 m 22 n 23
v 2 l21 2 m 22 2 n 23 2 v 2
l2m 2n21
1 2 a , 2 0 , 3 a
ma x1 23
3a 2
39
例2：已知某点的应力状态为： x 0, y 20, z 10, xy10, yz0, zx20
求：作用于过该点，方程为 3x 3y2z1 的平面外 侧的正应力和切应力。
解： l:m:n3: 3:2
l2m 2n21
p xl x m yx nzx p ylx ymy nzy p zlx zm y znz
李同林
• 工程弹塑性力学
杨伯源、张义同
• 工程弹塑性力学
毕继红、王晖
• 弹塑性力学引论
杨桂通
• 弹性力学（上、下册） 徐芝伦
• 塑性力学
夏志皋
• 岩土塑性力学原理 郑颖人 沈珠江
. 14
第一章 应力分析
§ 1－1 应力状态 § 1－2 应力张量及分解 § 1－3 等斜截面上的应力、应力状态参数 § 1－4 平衡微分方程
x
a
lco ay,smsxyian
n
xco assian yco assian xy co2as
ax 2ysi2n axy co2as
37
3. 主应力和最大切应力
v 3I1v 2I2 vI30
I1xyzxy
I 2 xy yz zx x 2 y y 2 z z 2 xxy x 2y

弹塑性力学课件

弹塑性力学课件
i 1 j 1 2 2 2 2 2 31 31 32 32 33 33 x y z2 2 xy yz zx
3
3
方程 3 I1 I 2 I3 0 称为应力状态的特征方程， 它有三个实根，并规定
2 3 2 1 2 2
2
2 n 2 2 12 32 n1 2 1 3 n12 2 3 n2 3 2 1 3 n1 n1
1 3 2 2 4 1 3 n1 1 3 n1 2 3 n2 3 2 1 3 2 2 4 1 3 n1 1 3 n1 2 3 n2 0 2 1 3 2 2 n1 1 3 n1 2 3 n2 0 2
位移矢量的分解
3
u ux ex u y ey uz ez u1e1 u2e2 u3e3 ui ei
i 1
一点的应力状态
z
z
zy yz
zx
x
x
xz
xy yx
y
y
一点的应力状态
z
N τyx τxy σy σx τxz τzx σz y
τyz τzy
2 2 2 J 2 S x S y S y S z S z S x S xy S yz S zx
1 2 2 2 2 S x S y S y S z S z S x S x S y S y S z S z S x S xy S yz S zx 3 1 2 2 2 2 2 S x S y S z2 S x S y S y S z S z S x S xy S yz S zx 3 2 2 1 2 2 2 2 S x S y S y S z S z S x S xy S yz S zx 6 1 2 2 2 S1 S 2 S 2 S3 S3 S1 6 1 2 2 2 1 2 2 3 3 1 6

弹塑性力学第三章 应力与应变讲解

弹塑性力学第三章 应力与应变讲解
pn nn ns (3.2)
式中：n和s分别为微分面的法线和切线方向的单位 矢量。全应力和应力分量之间有
n pn n

n pn s
pn2


2 n

(3.3)
研究具体问题时，总是在一个可以选定坐标系里进 行。对给定的直角坐标系，全应力还可以沿坐标系 方向进行分解。
p 的单位法向量，它与三个坐标轴之间的夹角余弦为 l1、l2、l3
则该主平面上的应力矢量 n 可表示为
pn n (3.14)
或
px py
l1 l2

(3.15)
pz
l3

式中： 表示主应力
将应力分量表达式(3.7)代入上式，经移项并整理后得
(
x


)l1
设给定的坐标系Oxyz下，某点M的应力张量为
ij yxx
xy y

xz yz

zx zy z
现让该坐标系原点不动，坐标轴任意旋转一个角度而得 到新坐标系Ox’y’z’,新旧坐标关系如下表：
x
y
z
X’ l11 cos(x ', x) l12 cos(x ', y) l13 cos(x ', z)
要使主方向存在，也即要使方程组（3.17)或（3 .18)有 非零解，则其系数行列式必须为零。
x yx zx
xy y
zy
xz yz 0 z
(3.19a)
方程组(3.19)也可以写成
det ij ij 0
(3.19b)
式（3.19)展开后，得
对面）上有9个应力分量。这9个应力分量的整

弹塑性力学1 应力分析PPT课件

弹塑性力学1 应力分析PPT课件

xy
x
y
斜截面法向 斜截面切向
xy
x S v
Scos
v
y Ssin
静力平衡 方程
(注意应 力符号规
定)
vS(xScos)cos(ySsin)sin (xyScos)sin(xySsin)cos
vS(xScos)sin(ySsin)cos (xySsin)sin(xyScos)cos
斜截面上的应力 分量计算公式
如果作用在物体表面上的外面载荷用Fx，Fy，Fz表 示，而斜面为边界面，此时上式中的Pvx,Pvy,Pvz都换 成Fx，Fy，Fz，则上式亦可作为应力边界条件。
总应力 pv pv2xpv2ypv2z
正应力 vlP vxmvP ynvPz
l2x m 2y n 2z 2 lm x y 2 m y z n 2 nzl x
原因：一旦应力状态确定后，其主应力便已确定，当坐标变 换时，虽然每个应力分量都将随之变化，但主应力的值是不 变的。所以Ii的值是不变的。
（应力不变量的意义）
主应力空间
vlP vxmvP ynvPzl21m22n23
pv2pv2xpv2ypv2z l21 2 m 22 2 n 23 3v 2v 2
x v yx zx
xy y v
zy
xz yz 0 z v
v 3I1 v 2I2 vI30
1,2,3 li, mi, ni
应力不变量
I1xyz
I2xyyzzx x 2 yy 2 zz 2x
I 3 xyz 2 xy yz z xxy 2 zyz 2 xzx 2y
当坐标变换时，应力不变量的值是不变的。
l2 m2 n2 1
0
l2 1v2( (1v2)2 ()1 (v3 )3)

弹性问题的应力解法

弹性问题的应力解法

弹性问题的应力解法
一、背景介绍
弹性是在结构应力影响下出现的变形。

它指结构受力时，坐标系中有限数量的点发生形变，使结构暂时失去平衡，但当外力消失时，原来的状态可以被恢复。

把物体的变形actions 把物体的变形分析也得到把物体的变形描述的开发应力分步骤，这就是应力解法。

二、应力解法
应力解法是一种微分解法，用于计算弹性受力时物体变形的步骤如下：
（1）首先，我们必须考虑物体所有平面构成以及每一片的体积单元量。

这样，我们就可以计算出物体的变形量。

（2）然后，我们可以计算出这些变形量之间的联系，即利用应力解法来求解能量量。

（3）最后，接下来我们需要确定一个参数用来表示应力的变化，这个参数就是屈服极限。

屈服极限是指在应力达到极限之前，物体能承受的最大应力，它通常用分母断面积来表示。

（4）最后，我们采用屈服极限和变形量作为应力解法的两个参数，利用这两个参数计算出整体上的变形量，从而得到最终的结果。

三、结论
对于弹性物体的变形，应力解法是一种简便有效的方法。

它将变形体积单元量与屈服极限相结合，从而有效地计算出受力时物体变形的量，有效地求解出整体变形量，使得最终计算结果更加准确可靠。

弹塑性力学_第7章 应力分析

弹塑性力学_第7章 应力分析


上述方程可以改写成如下形式
I1 I 2 I3 0
3 2

三个应力不变量
I1 x y z
2 2 I 2 y z z x x y 2 xy yz zx 2 2 2 I 3 x y z x yz y zx z xy 2 yz zx xy

解得
l 2 2 m 2 2 n 2 2

于是
1 =
2 - 3
σ3
2 3 - 1 2= 2 1 - 2 3 = 2
σ1
σ2
§7-5 等倾面上的正应力


等倾面的概念 等倾面的方向 l2+m2+n2=1 等倾面上的正应力
1 3 l mn 3 3
1 v ( 1 2 3 ) 3

等倾面上的剪应力
v2 pv2 v2 1 2 1 2 2 ( 1 2 3 ) ( 1 2 3 ) 2 3 9 1 [2( 12 22 32 ) 2( 1 2 2 3 3 1 )] 9 1 [( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 ] 9
由于上式l2、m2、n2恒为正，右边分子分母同号。 设σ 1＞ σ 2 ＞ σ 3，第二式分母为负，分子必为负
2 ( v 1 )( v 3 ) v 0

也就是
τ
( v

1 3
2
) (
2 2 v
1 3
2
)2
σ3 σ2 σ1
同理
( v
τ

令

弹塑性力学 应力函数求解

弹塑性力学 应力函数求解
显然应力函数所对应的面力在梁两端与本题相一致只是该函数在上下边界面上多出了一个大小为的剪应力为了抵消它在应力函数再添加一个与纯剪应力对应的应力函数axybxyxybxyxybhdy3ay自然满足自然满足10例题4图示的墙高度为h宽度为b两侧受均布剪力作用用已知应力函数求解应力分量bxaxy解
例题1如图所示的简支梁只承受自重的作用，设材料的密度 为 ，给出 ( x, y) 函数可以作为应力函数的条件，并求 出 ( x, y) 表达式和应力分量，其中， ( x, y) 的形式为：
( x, y) Ax 2 y 3 By 5 Cy 3 Dx 2 y
解： 将应力函数代入相容方程, 2 2 0 得到
A 5B 这就是作为应力函数必须满足的条件 此时： 2 3 5 3
4 4 2 4 0; 4 120y; 2 2 2 12Ay 24Ay 4 x y x y
x gx cot gy cot2 y gy xy gy cot
14
15
0 b/2
b
-b/2 b/2
xy dx 0 -

-b/2
-b/2
Bb3 A 3Bx2 dx 0 Ab 0 4
x 0 12q y 2 xy b q x2 xy 1 - 12 2 2 b
x 2 xy -A - 3Bx2 在x b/2边界上, x 0自然满足 xy 3Bb2
Axy Bx y
3
xy -q A
4
q
10
在y 0 边界上
b/2
y dx 0
满足; y xdx 0满足
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

V x V F y y F x
式子中的V为体力势函数。 同样可以引进一个airy函数，使得他满足下面的 关系式 2 x V 2
y
此时微分方程自动满足
y
xy
2 V x 2 2 xy
Company Logo
弹塑性平面问题的应力函数解法
Z
将上式 代入本构方程得平 面 方程
应力问题中的物理方程即
1 x y E 1 y y x E
应变问题中的物理
x
1 xy G E 其中G 21
xy
1 2 x ( x y) E 1 1 2 y ( y x) E 1 21 xy xy E z xz yz 0
E∕(1-υ^2)，υ换为υ∕(1-υ)，就
- - x y
2 2 x y 2 y
x
21
2 x

xy y
得到平面
应变物理方程
将平 使它只包含正应力而不包含切应力。 为此将下式平衡微分方程对x y 求 导
2.或者用应力函数表示体积力势为常数的情 况----
2 2 l1 l2 X y 2 xy 2 2 2 l1 2 l2 Y y x
Company Logo
热烈欢迎
吕龙生同学
• 将它代入应变协调方程得
4 (1 v) 2V
• 上式就是有势体力作用下弹性平面问题要 求满足的基本方程。
Company Logo
弹塑性平面问题的应力函数解法
上面我们讲到了体积力不同，会产生的两种 不同的方程。对于同是外力的面积力我们也 是要求求解的。特别是对于边界条件而言， 研究应力函数的时候，也需要将静力边界条 件给出。 1.有体积力势的情况 --- xl1 xy l2 X yx l1 y l2 Y

相容方程可简化为
( x y ) 0
2
引进函数 ，使得它 满足如下的关系式
x, y
2 2 4 0 4 x x y y
4 4 4
x 2 / y 2 y 2 / x 2 xy 2 / xy
2 2 2 2 2 xy y x 2 y 2 x x
求导后然后相加，注意到xy 面的切应力等于yx面的切应 力所以得
y
1.考虑体力是长量的情况 • 采用应力法求解弹性平面问题的一-特殊解法---应力函数求解法 • 在不计体积力的时候即Fx和Fy等于0， 弹性平面问题满足的平衡微分方程可 化简为
将上式代入到
其中是拉普拉 斯算子
2 2 2 x 2 y 2 z 2
• 将airy函数代入平衡微 分方程，则平衡方程 自动满足，代入应变 协调方程 得到
上式可简化为
0
4 2 2
弹塑性平面问题的应力函数解法
2. 体力为有势的情况 即 代入平面微分方程化为
( x V ) xy 0 x y xy ( y V ) 0 x y
报告人：01031
弹塑性平面问题的应力函数解法
弹性力学的基本解 法
位移法
应力法.
应力函数需要满足 哪些条件呢
应力法
平衡条件 几何条件
本构条件
Company Logo
弹塑性平面问题的应力函数解法
有面积力 有体积力
总述方向
无体积力 无面积力
Company Logo
在平面问题中 =0，带入到本构方程得平面
平面问题中，因为物体各点都不沿z 方向移动，所哟在z方向线段都没有 伸缩，即 0 所以
Z

Z x y
通过上式可以看出，两种平 面问题的物理方程是不一样 的。然而，如果在平面应
2
2 2 2 x y xy 2 得 y 2 x xy
力问题的物理方程将E换为
- - 21 x y
2 2 2 2 x y 2 y x x
xy y
xy x 0 0 x y xy y 0 0 x y
得相容方程
2 x y
f x f y 1 x y
1 x y E 1 y y x E 21 代入到本构方程 xy xy E
x
x xy fx 0 x y xy x y y fy 0


f f 2 x y x y