最短路问题(整理版)
- 格式:doc
- 大小:81.92 KB
- 文档页数:8

§6.2最短路问题2.1 两个指定顶点之间的最短路径问题如下:给出了一个连接若干个城镇的铁路网络,在这个网络的两个指定城镇间,找一条最短铁路线。
以各城镇为图G 的顶点,两城镇间的直通铁路为图G 相应两顶点间的边,得图G 。
对G 的每一边e ,赋以一个实数)(e w —直通铁路的长度,称为e 的权,得到赋权图G 。
G 的子图的权是指子图的各边的权和。
问题就是求赋权图G 中指定的两个顶点00,v u 间的具最小权的轨。
这条轨叫做00,v u 间的最短路,它的权叫做00,v u 间的距离,亦记作),(00v u d 。
求最短路已有成熟的算法:迪克斯特拉(Dijkstra )算法,其基本思想是按距0u 从近到远为顺序,依次求得0u 到G 的各顶点的最短路和距离,直至0v (或直至G 的所有顶点),算法结束。
为避免重复并保留每一步的计算信息,采用了标号算法。
下面是该算法。
(i) 令0)(0=u l ,对0u v ≠,令∞=)(v l ,}{00u S =,0=i 。
(ii) 对每个i S v ∈(i i S V S \=),用)}()(),({min uv w u l v l iS u +∈ 代替)(v l 。
计算)}({min v l iS v ∈,把达到这个最小值的一个顶点记为1+i u ,令}{11++=i i i u S S 。
(iii). 若1||-=V i ,停止;若1||-<V i ,用1+i 代替i ,转(ii)。
算法结束时,从0u 到各顶点v 的距离由v 的最后一次的标号)(v l 给出。
在v 进入i S 之前的标号)(v l 叫T 标号,v 进入i S 时的标号)(v l 叫P 标号。
算法就是不断修改各项点的T 标号,直至获得P 标号。
若在算法运行过程中,将每一顶点获得P 标号所由来的边在图上标明,则算法结束时,0u 至各项点的最短路也在图上标示出来了。
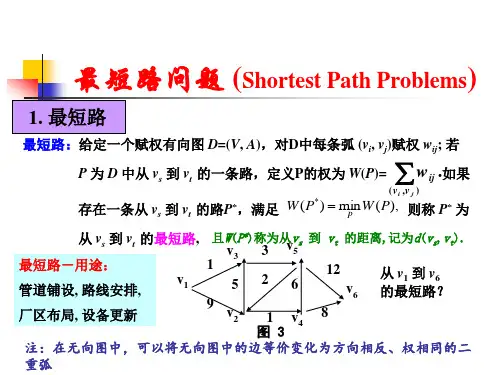
例9 某公司在六个城市621,,,c c c 中有分公司,从i c 到j c 的直接航程票价记在下述矩阵的),(j i 位置上。


§ 3最短路问题在实践中常遇到的一类网络问题是最短路问题。
给定一个有向赋权图D=(V,A),对每一个弧a =( ,),相应有权≥0,指定D中的为发点,为终点。
最短路问题就是要在所有到的路中,求出一条总权数最小的路。
这里权数可以是距离,也可以是时间,或者是费用等等。
最短路问题是最重要的优化问题之一,它不仅可以直接应用于解决生产实际的许多问题,如管道铺设、线路安排、厂区布局、设备更新等等,而且经常被作为一个基本工具,用于解决其它优化问题。
3.1 狄克斯拉(Dijkstra)算法最短路问题可以化为线性规划问题求解,也可以用动态规划方法求解,这里介绍一种有效算法—狄克斯拉(Dijkstra)算法,这一算法是1959年首次被提出来的。
该算法适用于每条弧的权数≥0情形。
算法的基本思路:从发点出发,有一个假想的流沿网络一切可能的方向等速前进,遇到新节点后,再继续沿一切可能的方向继续前进,则最先到达终点的流所走过的路径一定是最短的。
为了实现这一想法,对假想流依次到达的点,依次给予p标号,表示到这些点的最短距离。
对于假想流尚未到达的点给予T标号,表示到这些点的最短距离的估计值。
具体作法如下:1°标p()=0,其余点标T()=+∞;2°由刚刚获得p标号的点出发,改善它的相邻点的T标号,即新的T()=min{老的T(),p()+ }若T()= p()+ ωij ,则记k()=(前点标记);3°找出具有最小T标号的点,将其标号改为p标号。
若已获得p标号,则已找到最短路,由k ()反向追踪,就可找出到的最短路径,p()就是到的最短距离。
否则,转2°。
例2 求图下中v1 到v8 的最短路。
解:标p()=0,其余点标将具有最小T标号的点的标号改为p标号:p()=3;目前,点具有最小T标号,将其标号改为p标号: p()=4;目前,点具有最小T标号,将其标号改为p标号: p()=5;目前,点具有最小T标号,将其标号改为p标号: p()=6;目前,点具有最小T标号,将其标号改为p标号:最短路径为:因p()=12,所以→的最短距离为12。

最短路问题可以分为两类:单元最短路求从⼀个点到其他所有点的最短距离,如从1号点到n号点的最短路多源汇最短路起点和终点数量不确定n表⽰图中点的数量,m表⽰图中边的数量,⼀般m~n2是稠密图朴素Dijkstra适合稠密图,如边数⽐较多和n2⼀个级别⽤朴素Dijkstram和n是⼀个级别,堆优化版⽐较好SPFA是Bellman-Ford算法的⼀个优化,但是在某些时候SPFA是不能使⽤的,如对边数进⾏⼀个限制,经过不超过k条边就只能⽤Bellman-Ford最短路不会让你去证明算法的正确性,最短路的难点在于如何把原问题抽象成最短路问题,如何定义我们的点和边使得这个问题变成⼀个最短路问题,从⽽套⽤公式去解决。
难点在于建图。
Dijkstra基于贪⼼,Floyd基于动态规划,Bellman-Ford基于离散数学。
1、Dijkstra算法⼀定不能存在负权边。
伪代码:1. 初始化距离:dis[1] = 0,dis[others] = +∞。
2. 集合s:存储当前已经确定最短路的点3. for(int i = 0;i < n; i++) {t←找到不在s中的距离最近的点s←to⽤t更新其他点的距离。
更新⽅式:看从t出去的所有的边,组成的路径能不能更新其他点的距离。
如下图:如果从1到x的距离⼤于从1到t再到x的距离,就⽤dis[t]+w代替1到x的距离。
如下图:初始状态:①②③上的数字表⽰距离起点的距离,红⾊表⽰待定,绿⾊表⽰确定已经放⼊了集合s。
第⼀个点更新:第⼆个点更新:第三个点更新:}1.1 Dijkstra练习1.2 朴素Dijkstra算法解答存在重边只保留最短的那条边就可以了解答:if (!st[j] && (t == -1 || dist[t] > dist[j]))#include <cstring>#include <iostream>#include <algorithm>using namespace std;const int N = 510;int n, m;int g[N][N];int dist[N]; // 从1号点⾛到其他每个点当前最短距离bool st[N];int dijkstra(){memset(dist, 0x3f, sizeof dist);dist[1] = 0;for (int i = 0; i < n - 1; i ++ ){int t = -1; // 初始还没有确定点的时候for (int j = 1; j <= n; j ++ )// 这个循环找的就是所有st[j]=false即距离还没确定的点 // 在这些点中找到距离最⼩的点if (!st[j] && (t == -1 || dist[t] > dist[j]))t = j;for (int j = 1; j <= n; j ++ )dist[j] = min(dist[j], dist[t] + g[t][j]);st[t] = true;}if (dist[n] == 0x3f3f3f3f) return -1;return dist[n];}int main(){scanf("%d%d", &n, &m);memset(g, 0x3f, sizeof g);while (m -- ){int a, b, c;scanf("%d%d%d", &a, &b, &c);g[a][b] = min(g[a][b], c); // 取min是可能存在重边}printf("%d\n", dijkstra());return 0;}1.3堆优化Dijkstra算法解答考虑如何优化:因为t从1~n每次都是不同的点,所以⽤t更新其他点的距离这个操作就是遍历从t出去所有边,遍历n次即遍历所有点以后就是遍历了所有边,所以计算了m次可以发现最慢的就是找最⼩距离这步,复杂度O(n2)。

最短路问题何谓最短路?最短路问题考虑的是有向网络N=(V,A,W),其中弧(i,j)∈A 对应的权又称为弧长或费用。
对于其中的两个顶点s,t∈V,以s 为起点,t 为终点的有向路称为s-t 有向路,其所经过的所有弧上的权(或弧长、费用)之和称为该有向路的权(或弧长、费用)。
所有s-t 有向路中权最小的一条称为s-t 最短路。
ij w 如何得到最短路?最短路问题的线性规划描述如下:(,)m i ni j i j i j A w x ∈∑ (1):(,):(,)1,,..1,,0,,ij ji j i j A j j i A i s s t x x s i s t ∈∈=⎧⎪t −=−=⎨⎪≠⎩∑∑ (2) 0ij x ≥ (3) 其中决策变量表示弧(i,j)是否位于s-t 路上:当=1时,表示弧(i,j)位于s-t 路上,当=0时,表示弧(i,j)不在s-t 路上。
本来,应当是0-1变量,但由于约束(2)的约束矩阵就是网络的关联矩阵,它是全幺模矩阵,因此0-1变量可以松弛为区间[0,1]中的实数(当用单纯形法求解时,将得到0-1整数解)。
ij x ij x ij x ij x 值得注意的是,我们这里将变量直接松弛为所有非负实数。
实际上,如果可以取0-1以外的整数,则约束条件并不能保证对应于非零的弧所构成的结构(记为P)一定是一条路,因为这一结构可能含有圈。
进一步分析,我们总是假设网络本身不含有负圈,而任何正圈不可能使目标函数最小,因此上面的约束条件(2),(3)可以保证当达到最优解时,P 如果包含圈,该圈一定是零圈,我们从P 中去掉所有的零圈,就可以得到最短路。
ij x ij x ij x 无圈网络与正费用网络一般采用标号设定算法。
Bellman 方程(最短路方程)将约束条件(2)两边同时乘以-1,得到其对偶问题为:m ax()t s u u − (4)..,(,)j i ij s t u u w i j A −≤∀∈ (5)根据互补松弛条件,当x 和u 分别为原问题和对偶问题的最优解时:()0,(,i j j i i j )x u u w i j −−=∀∈A (6) 因此,当某弧(i,j)位于最短路上时,即对应的变量>0时,一定有ij x j i i u u w −=j 。



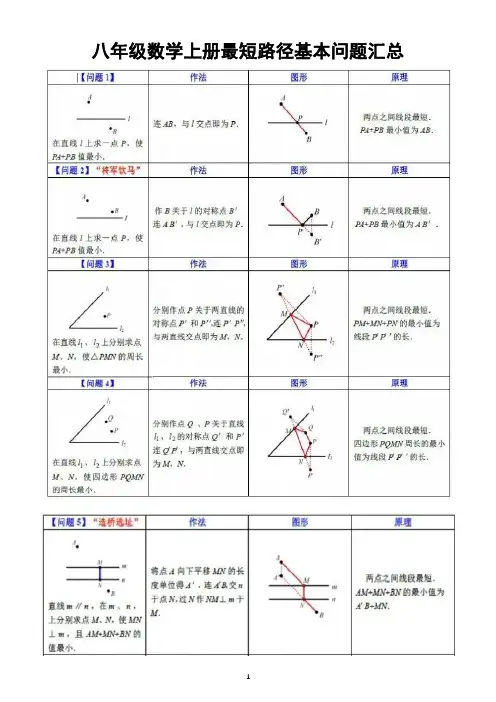
八年级数学上册最短路径基本问题汇总
经典例子解析
例一、在解决最短路径问题时, 我们通常利用_____、_____等变换把已知问题转化为容易解决的问题,从而作出最短路径的选择。
例二、已知,如图,在直线l的同侧有两点A、 B
例三图例四图
(1)在图1的直线上找一点P使PA+PB最短;(2)在图2的直线上找一点P,使PA-PB最长
例三、如上图所示,P为∠AOB内一点,P1,P2分别是P关于OA,OB 的对称点,P1P2交OA于M,交OB于N,若P1P2=8 cm,则△PMN的周长是( )
A.7 cm
B.5 cm
C.8 cm
D.10 cm
例四、如图,在等腰Rt△ABC中,D是BC边的中点,E是AB边上一动点,要使EC+ED最小,请找点E的位置例五、如图,村庄A,B位于一条小河的两侧,若河岸a,b彼此平行,现在要建设一座与河岸垂直的桥CD,问桥址应如何选择,才能使A村到B村的路程最近?
参考答案
例一:轴对称平移
例二:(1)作点B关于直线l的对称点C,连接AC交直线l于点P,连接BP;点P即为所求(2)连接AB并延长,交直线l于点P
例三:C
例四:作点C关于AB的对称点C′,连接C′D与AB的交点为E点
例五:①过点A作AP⊥a,并在AP上向下截取AA′,使AA′=河的宽度;②连接A′B交b于点D;③过点D 作DE∥AA′交a于点C;④连接AC.则CD即为桥的位置。
最短路问题详解+题⽬概念若⽹络中的每条边都有⼀个数值(长度、成本、时间等),则找出两节点(通常是源节点和阱节点)之间总权和最⼩的路径就是最短路问题算法1. Floyd-warshall算法(1)介绍:⾮常的好⽤,通常可以在任何图中使⽤,包括有向图、带负权边的图。
(2)算法讲解:Floyd算法从第⼀个顶点开始,依次将每个顶点作为媒介k,然后对于每⼀对顶点u和v,查看其是否存在⼀条经过k的,距离⽐已知路径更短的路径,如果存在则更新它。
2. Dijkstra算法(1)介绍:是典型的单源最短路径算法,⽤于计算⼀个节点到其他所有节点的最短路径。
主要特点是以起始点为中⼼向外层层扩展,直到扩展到终点为⽌。
注意该算法要求图中不存在负权边。
(2)算法讲解:⽤贪⼼实现,先把起点到所有点的距离存下来找个最短的,进⾏松弛操作再找出最短的,把所有的点找遍之后就存下了起点到其他所有点的最短距离。
> 松弛操作:遍历⼀遍看通过刚刚找到的距离最短的点作为中转站会不会更近,如果更近了就更新距离> 注意:除了距离起点的距离为0外,其他距离均设为⽆穷⼤。
3. Bellman-Ford算法(1)介绍:Bellman-ford算法适⽤于单源最短路径,图中边的权重可为负数即负权边,但不可以出现负权环。
> 负权边:为负数的边。
> 负权环:源点到源点的⼀个环,环上权重和为负数。
(2)算法讲解:1.初始化:除了起点的距离为0外,其他均设为⽆穷⼤。
2.迭代求解:循环对边集合E的每条边进⾏松弛操作,使得顶点集合V中的每个顶点v的距离长逐步逼近最终等于其最短距离长;3.验证是否负权环:再对每条边进⾏松弛操作。
如果还能有⼀条边能进⾏松弛,那么就返回False,否则算法返回True题⽬输⼊:第⼀⾏n表⽰边的个数,接下来n⾏a,b,len,最后⼀⾏s,t求点s到点t的距离输⼊样例:71 2 22 5 21 3 42 3 13 5 61 4 73 4 1Dijkstra打法#include <bits/stdc++.h>#define maxx 0x7fusing namespace std;int u[105][105]={0x7f},dis[105];bool vis[105]={false};int main(){int n,s,t,x,y,minn,k;cin>>n;for (int i=1;i<=n;i++){dis[i]=maxx;vis[i]=false;}for (int i=1;i<=n;i++)for (int j=1;j<=n;j++)u[i][j]=maxx;for (int i=1;i<=n;i++){cin>>x>>y;cin>>u[x][y];}cin>>s>>t;for (int i=1;i<=n;i++)dis[i]=u[s][i];dis[s]=0;vis[s]=true;for (int i=1;i<=n;i++){minn=maxx;k=0;for (int j=1;j<=n;j++)if (vis[j]==false&&dis[j]<minn){minn=dis[j];k=j;}if (k==0) break;vis[k]=true;for (int j=1;j<=n;j++)if (dis[k]+u[k][j]<dis[j])dis[j]=dis[k]+u[k][j];}cout<<dis[t];return 0;}floyd打法#include <bits/stdc++.h>using namespace std;const int maxx=0x7f;int u[105][105];int main(){int s,t,n,x,y;cin>>n;for (int i=1;i<=n;i++)for (int j=1;j<=n;j++)u[i][j]=0x7f;for (int i=1;i<=n;i++){cin>>x>>y;cin>>u[x][y];}cin>>s>>t;for (int k=1;k<=n;k++)for (int i=1;i<=n;i++)for (int j=1;j<=n;j++){if (i!=j&&i!=k&&j!=k&&u[i][j]>u[i][k]+u[k][j])u[i][j]=u[i][k]+u[k][j];}cout<<u[s][t];return 0;}题⽬⼤意找⼀个点使得到其他点的距离总和最⼩Floyed穷举出答案#include <bits/stdc++.h>using namespace std;const int inf=100000007;int p[105],dis[105][105],sum;int n,lch,rch;int main(){cin>>n;memset(dis,inf,sizeof(dis));for(int i=1;i<=n;i++){dis[i][i]=0;cin>>p[i];cin>>lch>>rch;if(lch>=0) dis[i][lch]=1;dis[lch][i]=1;if(rch>=0) dis[i][rch]=1;dis[rch][i]=1;}for(int k=1;k<=n;k++)for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)if(dis[i][j]>dis[i][k]+dis[k][j]) dis[i][j]=dis[i][k]+dis[k][j]; int minn=inf;for(int i=1;i<=n;i++){sum=0;for(int j=1;j<=n;j++)sum+=p[j]*dis[i][j];if(minn>sum) minn=sum;}cout<<minn<<endl;return 0;}。
作业:课堂作业:书本P182第5题第(1)题()⎩⎨⎧=)这条弧,未经过(这条弧,经过(j i j ij V V V V f 0)(1i 6714131220...81510min f f f f z ++++=()()()()⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧===-=+-=-+++=+-+=++-=+++-=-+=++7,6,5,4,3,2;6,5,4,3,2,1101000000001675767656463652557536434146353231334122523141312j i f f f f f f f f f f f f f f f f f f f f f f f f f ij,或 最短路径为7521v v v v ---课后作业:1、 求下列赋权无向网络图s 到t 的最短路径P:∑∈=Av v ijijj i f wz ),(min()⎪⎪⎩⎪⎪⎨⎧=-=-≠=-==-∈=∑∑∑∑∑∑t i f f t s i f f si f f A v v f ji ij jiij ji ij j i ij ,1,,0,110,,或 最短路径为S-3-5-T2、某公司正在研制一种有极好销售潜力的新产品。
当研究工作接近完成时,公司获悉一家竞争者正计划生产这种产品。
要突击赶制出这种产品以参与竞争,还有四个互不重叠的阶段。
为了加快进度,每个阶段都可采取“优先”或“应急”的措施。
不同的措施下每段工作所需要的时间(月)和费用(百万元)如小下表示。
现有一千万元资金供这四个阶段使用,则每段应采取什么措施能使这种产品尽早上市。
试将此问题化成最短路问题并求解。
43131211...245min f f f f Z ++++=⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=====++=++=++=++3,2,1;4,3,2,1100,,1111413121434241333231232221131211j i f f f f f f f f f f f f f f f f ij ,或 解得在一千万元资金供应的条件下最短时间为10个月。
最短路问题(short-path problem)若网络中的每条边都有一个权值值(长度、成本、时间等),则找出两节点(通常是源节点与结束点)之间总权和最小的路径就是最短路问题。
最短路问题是网络理论解决的典型问题之一,可用来解决管路铺设、线路安装、厂区布局和设备更新等实际问题。
最短路问题,我们通常归属为三类:单源最短路径问题(确定起点或确定终点的最短路径问题)、确定起点终点的最短路径问题(两节点之间的最短路径)1、Dijkstra算法:用邻接矩阵a表示带权有向图,d为从v0出发到图上其余各顶点可能达到的最短路径长度值,以v0为起点做一次dijkstra,便可以求出从结点v0到其他结点的最短路径长度代码:procedure dijkstra(v0:longint);//v0为起点做一次dijkstrabegin//a数组是邻接矩阵,a[i,j]表示i到j的距离,无边就为maxlongintfor i:=1 to n do d[i]:=a[v0,i];//初始化d数组(用于记录从v0到结点i的最短路径), fillchar(visit,sizeof(visit),false);//每个结点都未被连接到路径里visit[v0]:=true;//已经连接v0结点for i:=1 to n-1 do//剩下n-1个节点未加入路径里;beginmin:=maxlongint;//初始化minfor j:=1 to n do//找从v0开始到目前为止,哪个结点作为下一个连接起点(*可优化) if (not visit[j]) and (min>d[j]) then//结点k要未被连接进去且最小begin min:=d[j];k:=j;end;visit[k]:=true;//连接进去for j:=1 to n do//刷新数组d,通过k来更新到达未连接进去的节点最小值,if (not visit[j]) and (d[j]>d[k]+a[k,j]) then d[j]:=a[k,j]+d[k];end;writeln(d[n]);//结点v0到结点n的最短路。
思考:在实现步骤时,效率较低需要O(n),使总复杂度达到O(n^2)。
对此可以考虑用堆这种数据结构进行优化,使此步骤复杂度降为O(log(n))(总复杂度降为O(n log(n))。
实现:1. 将与源点相连的点加入堆(小根堆),并调整堆。
2. 选出堆顶元素u(即代价最小的元素),从堆中删除,并对堆进行调整。
3. 处理与u相邻(即下一个)未被访问过的,满足三角不等式的顶点1):若该点在堆里,更新距离,并调整该元素在堆中的位置。
2):若该点不在堆里,加入堆,更新堆。
4. 若取到的u为终点,结束算法;否则重复步骤2、3。
**优化代码:(DIJKSTRA+HEAP)program SSSP;{single source shortest path}{假设一个图的最大节点数为1000,所有运算在integer范围内}{程序目标:给定有向图的邻接表,求出节点1到节点n的最短路径长度}const maxn=1000;{最大节点数}varn:integer;{节点个数}list:array[1..maxn,1..maxn] of integer;{邻接矩阵,表示边的长度}count:integer;{堆内元素个数计数器}heap:array[1..maxn] of integer;{heap[i]表示堆内的第i的元素的节点编号} pos:array[1..maxn] of integer;{表示编号为i的元素在堆内的位置}key:array[1..maxn] of integer;{表示节点1到节点i的最短距离}exist:array[1..maxn] of boolean;{表示节点i是否存在于堆中}i,j,now:integer;procedure swap(var i,j:integer);{交换整数i和j}//省略procedure heapify(p:integer);{向下调整堆的过程}var best:integer;beginbest:=p;//下面两个if是分别判断根和左、右孩子最短距离的大小if (p*2<=count) and (key[heap[p*2]]<key[heap[best]]) then best:=p*2;if (p*2+1<=count) and (key[heap[p*2+1]]<key[heap[best]]) then best:=p*2+1; if best<>p then//若根有所变动,即跟比左右孩子都大(最短距离)beginswap(pos[heap[p]],pos[heap[best]]);//互换节点heap[p]、heap[best]在堆的位置swap(heap[p],heap[best]);//互换堆中元素p、bestheapify(best);//继续调整互换后的元素bestend;end;procedure modify(id,new_key:integer);{判断new_key与key[id]大小,并修改key[id]大小}var p:integer;beginif (new_key<key[id]) thenbegin//修改key[id]:=new_key;//更新最短距离p:=pos[id];//结点id在堆中的位置while (p>1) and (key[heap[p]]<key[heap[p div 2]{父}]) do//向上调整beginswap(pos[heap[p]],pos[heap[p div 2]]);swap(heap[p],heap[p div 2]);p:=p div 2;//更上一层end;end;end;procedure extract(抽出)(var id,dis:integer);{读取堆中最小元素的节点编号和节点1到该节点的距离}beginid:=heap[1];//堆顶dis:=key[id];dec(count);//出堆if (count>0) then//堆里还有元素beginswap(pos[heap[1]],pos[heap[count+1]]);// 堆顶的元素和第count+1个元素换位置swap(heap[1],heap[count+1]);//把堆顶的元素扔到count后面去,heapify(1);//此时堆顶不一定是最小的~扔到下面去,把最小的搞上来。
end;end;beginreadln(n);init;//读入邻接矩阵,没有连线的为maxint;省略for i:=1 to n do{初始化}beginexist[i]:=true;//所有元素入堆pos[i]:=i; heap[i]:=i; key[i]:=maxint;end;count:=n; key[1]:=0;{dijkstra算法的主要操作}while (count>0) dobeginextract(i,now); exist[i]:=false;if now=maxint then break;//无路可走了,overfor j:=1 to n doif (exist[j]) then modify(j,now+list[i,j]);end;{输出}if key[n]=maxint then writeln('Not Connected!'){节点1和节点n不连通}else writeln(key[n]);{连通}end.SPFA+(前向星、循环队列、邻接表、链表)2、SPFA算法(Shortest Path Faster Algorithm):spfa算法是西南交通大学段凡丁于1994年发表的.简介:给定的图存在负权边时,dijkstra等便无用武之地,spfa算法便派上用场了。
若有向加权图G不存在负权回路,即最短路径一定存在,用数组d记录每个结点的最短路径估计值,用邻接表来存储图G。
采取方法是动态逼近法:设立一个队列用来保存待优化的结点,优化时每次取出队首结点u,且用到达u点当前的最短路径估计值d[u]对点u所指向的结点v进行松弛操作,若v点的最短路径估计值有所调整,且v点不在当前的队列中,就将v点放入队尾(已在队列里就不用放到队尾)。
这样不断从队列中取出结点来进行松弛操作,直至队列空为止。
若某点入队的次数超过n次,则存在负环,spfa无法处理这样的图。
定理: 只要最短路径存在,spfa算法必定能求出最小值。
证明:松弛操作原理:“三角形两边之和大于第三边”,在信息学中称三角不等式。
每次将点放入队尾,都是经松弛操作达到的。
所谓对i,j进行松弛,即if (d[j]>d[i]+w[i,j])then d[j]:=d[i]+w[i,j],每次优化都可能将某个点v的最短路径估计值d[v]变小,d数组将会越来越小。
由于图中不存在负权回路,所以每个结点都有最短路径值,算法不会无限执行下去,随着d值的逐渐变小,到最短路径值时,算法结束,这时的最短路径估计值就是对应结点的最短路径值。
时间复杂度:O(ke), k为所有顶点进队的平均次数,可以证明k一般小于等于2。
* 实现方法:建立一个队列,初始时队列里只有起始点,用d数组记录起始点到所有点的最短路径(该表格的初始值要赋为极大值,该点到他本身的路径赋为0)。
然后执行松弛操作,用队列里有的点去刷新起始点到所有点的最短路,如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。
重复执行直到队列为空求路径方案:若这幅图是地图的模型,除了算出最短路径长度,还要知道路径方案。
设path数组,path[i]表示从起点到i的最短路径中,结点i之前一个结点的编号,我们只需在结点u对结点v进行松弛时,标记下path[v]=u即可。
spfa算法采用邻接表来存储图,方法是动态优化逼近法。
算法中用队列queue用来保存待优化的结点,优化时从队首取出一个点w,并且用w点的当前路径d[w]去调整相连各点的路径值d[j],若有调整,即d[j]的值改小,就将j点放入queue队列以待进一步优化。
重复执行,直至队空。
此时d数组便保存了从起点到各点的最短路径值。
实例:设有向图g={v,e},e={<v0,v1>,<v0,v4>,<v1,v2>,<v1,v4>,<v2,v3>,<v3,v4>,<v4,v2>}={2,10,3,7,4,5,6},v={v0,v1,v2,v3,v4},见上图:算法执行时各步的queue队的值和d数组的值由下表所示。