当前位置：文档之家 › 最短路问题及其应用

最短路问题及其应用

  • 格式：doc
  • 大小：555.00 KB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

将士渡河——最短路径问题的实际应用

将士渡河——最短路径问题的实际应用

将士渡河——最短路径问题的实际应用引言最短路径问题是图论中的经典问题之一，它在现实生活中有着广泛的应用。

本文将讨论一个实际应用场景——将士渡河问题，并探讨如何使用最短路径算法来解决该问题。

问题描述将士渡河是一个经典的智力游戏，游戏规则如下：有一条河，河岸上有若干士兵和一艘船。

游戏目标是将所有士兵从一岸安全地运送到另一岸，而且船每次只能运送一定数量的士兵。

同时，游戏规定在任何一侧的岸边，士兵的数量不能超过敌军的数量，否则士兵将会被敌军消灭。

现在的问题是，如何通过最短路径算法确定士兵的最佳运输方案，以确保所有士兵都能安全渡河。

解决方案为了解决将士渡河问题，我们可以使用最短路径算法来确定士兵的最佳运输方案。

以下是解决该问题的步骤：1. 建立图模型：将河岸、士兵和船分别表示为图的节点，将船的运输能力表示为图的边。

根据游戏规则，我们可以将每一种状态（即河岸上士兵的分布情况）作为图的一个节点，并根据船的运输能力建立相应的边。

2. 权重设定：根据题目要求，我们需要找到最短路径来确保士兵的安全渡河。

因此，我们需要为图的每条边设定一个权重，使得最短路径算法能够在搜索过程中优先选择权重较小的路径。

可以根据士兵的数量、敌军的数量等因素来设定权重。

3. 应用最短路径算法：使用最短路径算法（如Dijkstra算法或A*算法）来确定从起点到终点的最短路径。

算法将根据权重和图的拓扑结构来搜索最短路径，直到找到目标节点或者搜索完整个图。

4. 输出结果：根据最短路径算法的结果，我们可以得到士兵的最佳运输方案。

可以将路径中的边转化为实际操作，即哪些士兵应该上船、哪些士兵应该下船，以及船的运输方向等。

实际应用将士渡河问题在实际生活中有着广泛的应用。

以下是一些例子：1. 军事行动：在实际的军事行动中，士兵的运输和部署是非常重要的。

通过使用最短路径算法，可以确定最佳的运输方案，以确保士兵能够安全快速地到达目的地。

2. 物流管理：在物流管理中，货物的运输是一个重要的环节。

医院选址问题——最短路的实际应用

医院选址问题——最短路的实际应用

医院选址问题——最短路的实际应用摘要：在求医院选址的问题中，将居民点与其之间的距离抽象成图论中的加权简单图。

而所求的“可使距离医院最远的小区居民就诊时所走的路程最近的小区”，则可已简化为图论中的最短路的模型。

在求解模型时，利用Floyd算法，通过MATLAB计算。

关键词：最短路；Floyd算法；MA TLAB问题的提出已知A 地区的交通网络如图1所示，其中点代表居民区，边表示公路，ij I 为小区间公路距离，问区中心医院建在哪个小区，可使距离医院最远的小区居民就诊时所走的路程最近?模型的建立问题的分析医院选址问题其实是一个求每一个节点到其他节点的最短路的问题。

而所选址则为到其他6个节点最短路中的最小值最小的节点，医院就应该建该节点所对应的居民小区。

简化的模型：可以将“A 地区交通网络图”看作一个简单图，其中包含有7个节点、9条边。

则可以写出其权矩阵D⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞=151518251530601830202560202015203030D 利用Floyd 算法，可以得到每一个节点到其他节点的最短距离。

最短路算法（Floyd 算法）通过7阶加权简单图的权矩阵D ，然后分别算出矩阵S D D D ,,...,,7]3[]2[，其中v 1v 2v 3v 5v 4 v 6v 7303060151520 2025 18 图1 A 地区交通网络图]7[]2[]1[][...,DDD S D DDi i ⊗⊗⊗=*=-则可得ij s 即为从节点i 到节点j 的所有路中距离最小者，即i 到j 的最短路。

其中，定义2种运算如下：模型的求解由权矩阵D ，通过Floyd 算法，用MA TLAB 求出了最短路矩阵S ：⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=0156333403060150481825154563480305063933318300203363402550200205030156333200306045936350300S则可得S 每个列向量中的最大值向量()63489363506393通过MATLAB 中的min1函数即可得到求得节点号6，即v6居民区为所求。

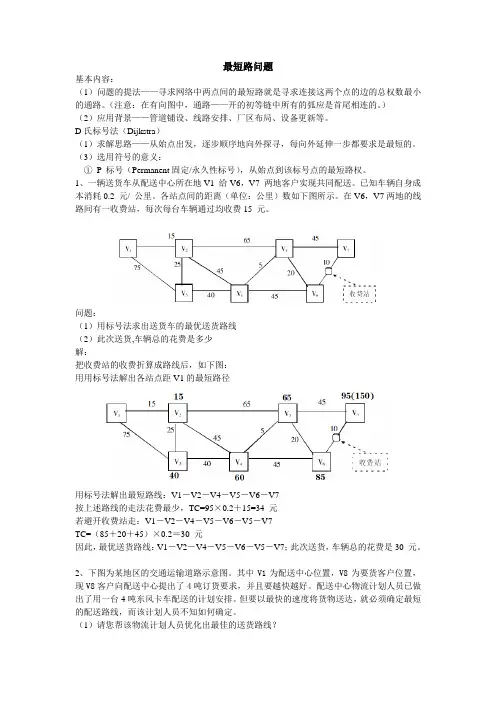
最短路问题

最短路问题

最短路问题基本内容：（1）问题的提法——寻求网络中两点间的最短路就是寻求连接这两个点的边的总权数最小的通路。

（注意：在有向图中，通路——开的初等链中所有的弧应是首尾相连的。

）（2）应用背景——管道铺设、线路安排、厂区布局、设备更新等。

D氏标号法（Dijkstra）（1）求解思路——从始点出发，逐步顺序地向外探寻，每向外延伸一步都要求是最短的。

（3）选用符号的意义：①P 标号（Permanent固定/永久性标号），从始点到该标号点的最短路权。

1、一辆送货车从配送中心所在地V1 给V6，V7 两地客户实现共同配送。

已知车辆自身成本消耗0.2 元/ 公里。

各站点间的距离（单位：公里）数如下图所示。

在V6，V7两地的线路间有一收费站，每次每台车辆通过均收费15 元。

问题：（1）用标号法求出送货车的最优送货路线（2）此次送货,车辆总的花费是多少解：把收费站的收费折算成路线后，如下图：用用标号法解出各站点距V1的最短路径用标号法解出最短路线：V1－V2－V4－V5－V6－V7按上述路线的走法花费最少，TC=95×0.2＋15=34 元若避开收费站走：V1－V2－V4－V5－V6－V5－V7TC=（85＋20＋45）×0.2＝30 元因此，最优送货路线：V1－V2－V4－V5－V6－V5－V7；此次送货，车辆总的花费是30 元。

2、下图为某地区的交通运输道路示意图。

其中V1为配送中心位置，V8为要货客户位置，现V8客户向配送中心提出了4吨订货要求，并且要越快越好。

配送中心物流计划人员已做出了用一台4吨东风卡车配送的计划安排。

但要以最快的速度将货物送达，就必须确定最短的配送路线，而该计划人员不知如何确定。

（1）请您帮该物流计划人员优化出最佳的送货路线？（2）已知车辆的平均行驶速度为50公里/小时，如早晨8：00发车，货物什么时间可以送达客户？解：用T 标号法求解得最短路线为：V1－Ｖ２－Ｖ３－Ｖ６－Ｖ７－Ｖ８。

最短路问题在旅游线路优化中的应用_曹旭

最短路问题在旅游线路优化中的应用_曹旭

end
线
路
k=k+1;
u=U(k1,k2);
优
end
%求任意给定的两个顶点间的最短路所包含的
化 中
P;
顶点
的
1.3 实例分析
P1=zeros(1,n);
应 用
求兰州火车站到麦积山的旅游最短距离和最短
k=1;
路。运行 Matlab 程序：
P1(k)=k2;
P=
V=ones(1,n)*inf;
1 2 14
１１６
k=k+1;
for j=1:n
end
if U(i,j)>U(i,m)+U(m,j)
end
U(i,j)=U(i,m)+U(m,j)
最 短
end
end
路
k=1;
end
问 题
wrow=find(P1~=0);
end
在
旅
for j=length(wrow): (-1):1
m=m+1
游
P(k)=P1(wrow(j));
如图一所示，通过上网收集到各个旅游景点之间的
距离如表一所示。在表一中，0 表示兰州火车站，1— 13 分别表示甘肃省及周边旅游景点兴隆山、嘉峪关
文物景区、拉卜楞寺、崆峒山、雷台、大佛寺、敦煌、黄
河石林、贵清山、青海湖鸟岛景区、塔尔寺、沙坡头、 麦积山。∞ 表示这两个旅游景点之间没有直接到达 的交通线路。如何求出任意两点之间的最短距离以 及最短路对旅客来说显得尤为重要，比如游客想从
在旅游过程中经常会遇到这样的问题：倘若在
kk=i;
任意旅游景点，想知道下一任意旅游景点的最短路。
k=k+1;

最短路问题实际案例

最短路问题实际案例

最短路问题实际案例介绍最短路问题是图论中的一个经典问题，其目标是找到两个顶点之间的最短路径。

这个问题在日常生活中有着广泛的应用，例如导航系统、网络路由以及物流配送等场景中都需要解决最短路问题。

本文将通过实际案例来深入探讨最短路问题及其应用。

什么是最短路问题？最短路问题是指在一个给定的图中，找到两个顶点之间的最短路径。

通常情况下，路径的长度可以通过边的权重来衡量。

最短路问题可以分为单源最短路问题和全源最短路问题，前者是指从一个固定的起点出发，求到图中其他所有顶点的最短路径；后者是指求图中任意两个顶点之间的最短路径。

实际案例：导航系统导航系统是最短路问题的一个典型应用。

当我们使用导航系统来规划路线时，系统需要找到最短路径以优化我们的行车时间。

下面以一个具体案例来说明导航系统如何解决最短路问题。

案例场景假设我们身处一座陌生的城市，想要前往城市中心的一个著名景点。

我们打开导航系统，输入起点和终点信息。

导航系统会根据地图数据自动生成最短路径，并提供导航指引。

导航系统的实现导航系统实现最短路径规划的过程可以分为以下几个步骤：1.构建路网图：将城市中的道路以及交叉口等信息转化为图的形式。

图中的节点表示交叉口，边表示道路，边的权重可以表示行驶距离、时间等。

2.选择算法：根据实际需求选择合适的最短路径算法。

常见的算法有Dijkstra算法、Bellman-Ford算法和A*算法等。

3.计算最短路径：根据选定的算法，在路网图上计算起点到终点的最短路径。

算法会考虑边的权重以及路径的方向等因素。

4.导航指引：根据计算得到的最短路径，导航系统会生成具体的导航指引，包括行驶指示、路口转向、距离和预计时间等信息。

优化策略导航系统通过不断的优化，提高了最短路径的计算效率和准确性。

以下是几种常见的优化策略：1.路网数据更新：导航系统会及时更新路网数据，包括道路信息、交通状况等。

这样可以保证计算得到的最短路径更准确。

2.平行算法：为了加快计算速度，导航系统采用并行算法来计算最短路径。

最短路问题数学模型

最短路问题数学模型

最短路问题数学模型
最短路问题是指在带权有向图中，求两个顶点之间的最短路径。

这个问题在现实生活中有很多应用，如在交通规划、电信网络设计、人工智能等领域。

为了解决这个问题，需要建立一个数学模型。

数学模型是指用数学方法对实际问题进行抽象和描述，从而进行定量分析和求解的方法。

对于最短路问题，可以使用图论和运筹学的方法建立数学模型。

在图论中，最短路问题可以使用迪杰斯特拉算法或弗洛伊德算法求解。

这些算法基于图的边权和，采用动态规划的思想，逐步计算每个节点到源节点的最短距离，最终得到整个图中每对节点之间的最短路径。

在运筹学中，最短路问题可以被看作是一种线性规划问题。

可以将每个节点看作是一个决策变量，节点之间的边权看作是线性约束条件，目标函数则是从源节点到目标节点的路径长度。

通过对目标函数进行最小化，可以得到最短路径的解。

总之，最短路问题数学模型可以通过图论和运筹学的方法进行建立和求解。

建立好的数学模型可以为实际问题提供科学解决方案，优化效率和效果。

- 1 -。

第六章 图与网络最短路径问题运筹学基础及其应用胡运权第五版

第六章 图与网络最短路径问题运筹学基础及其应用胡运权第五版

Ch6 Graph and Network
2012年12月31日星期一 Page 14 of 14
应用（教材P270例4） 年份 1 2 3 4 5
购置费 维修费
11 5
11 6
12 8
12 11
13 18
最优更新方案：1.第一年和第三年购置新设备；2.第一年和第四 年购置新设备。总费用为53。 59
Ch6 Graph and Network
2012年12月31日星期一 Page 12 of 14
**任意两点间最短距离的矩阵算法**（选讲） 【例】在下图中用矩阵计算法求各点之间的最短距离 【解】定义dij为图中两相邻点的距离，若i与j不相邻，令dij=∞。则 ② 5 ① 2 ③ 7 4 2 ④ 2 ⑥ 7 6 1 6 ⑤ 3 ⑦
v1 v2 v3 v4 0 －1 －2 3 6 0 －3 0 －5 0
－1 －1
v5
2
k=3 k=4 0 0 －5 －5
－2 －2
1
2 0 1 －3 0 1 0 －5
－7 －7 －7 1 －3 －3 －1 －1 －1 5 －5 －5 6 6
§6.3 最短路问题
Shortest Path Problem
当vi到vj之间没有弧连接时，令wij＝＋∞
列表迭代计算： 设vs到vj经过vi到达vj，则vs到vj的最短距离为： －2
①
3
② －2 ③
d (vs，v j ) min d (vs，vi ) wij
i
迭代：
d (1) (vs，v j ) wsj
i
d ( k ) (vs，v j ) min d ( k 1) (vs，vi ) wij

(最新整理)《最短路径问题》的反思及应用

(最新整理)《最短路径问题》的反思及应用

《最短路径问题》的反思及应用编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（《最短路径问题》的反思及应用）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为《最短路径问题》的反思及应用的全部内容。

《最短路径问题》的反思及应用我们知道，有效地开发和利用课本,对于学生的学习具有重要的意义。

学生对于课本上例题或习题能否吃透，直接影响着学生的学习效果。

因此教师要引导学生挖掘教材，引导学生进行反思,从中领悟问题解决过程的数学内涵.有这样一个问题：如图1所示，牧马人从地出发,到一条笔直的河边饮马,然后到地.牧马人到河边的什A l B么地方饮马，可使所走的路径最短?分析我们把河边近似看做一条直线 (如图2)，为直线上的一个动点，那么，上面的l P l问题可以转化为：当点在直线的什么位置时，与的和最小。

P l AP PB如图3所示，作点关于直线的对称点，连接，交直线于点，则点就是牧马AB l P PB l'B'人到河边饮马的位置。

事实上，点与点的线段最短，由对称性质知，，因为=PB PB'B A'AB'，即点到点、的距离之和最小。

+=+=P A BPA PB PA PB AB''上述路径问题，是利用轴对称的性质，通过等线段代换，将所求路线长转化为两定点之间的距离，基本思路是运用轴对称及两点之间线段最短的性质，将所求线段之和转化为一条线段的长。

从解题过程不难看出，本题蕴含着三个数学思想方法：数学模型思想，转化思想，对称思想.如果学生一旦认识或明白这些思想方法,就能举一反三,再复杂的问题也会迎刃而解。

最短路问题实际案例

最短路问题实际案例

最短路问题实际案例最短路问题是指在图中找出两个顶点之间的最短路径的问题，其中图可以是有向图或无向图，并且每条边可以有权重。

这个问题是在许多实际案例中都会遇到的。

以下是几个实际案例，其中涉及到最短路问题：1. 导航系统：导航系统是最常见的利用最短路问题的实例。

当用户输入起点和终点时，导航系统会计算出最短路径，并显示给用户。

这个过程中，导航系统需要考虑路程的时间或距离，同时还需要考虑道路的限速和交通情况等因素。

2. 物流配送：物流配送涉及到从一个地点到另一个地点的最短路径。

物流公司需要计算出从货物的起始点到目标点的最短路径，以最快速度将货物送达目的地。

在这个问题中，可能还会有其他限制条件，如运输工具的载重量、路段的通行能力等。

3. 电信网络：电信网络是一个复杂的网络，其中存在着许多节点和边，每个节点代表一个通信设备，边代表设备之间的通信连接。

在设计电信网络时，需要考虑到从一个节点到另一个节点的最短路径，以最小化通信的时延。

这个问题中，还会有其他因素，如网络拓扑的复杂性、网络流量的负载均衡等。

4. 交通规划：交通规划涉及到城市道路网络的设计和优化。

在设计城市交通规划时，需要考虑到不同节点之间的最短路径，以便在城市中建设高效的道路系统。

这个问题中，需要考虑到人口分布、交通流量、环境因素等复杂变量。

5. 谷歌地图：谷歌地图是一种广泛使用最短路径算法的应用。

当用户在谷歌地图上搜索起点和终点时，谷歌地图会计算出最短路径，并给出导航指引。

这个过程中，谷歌地图需要考虑到道路的限速、交通情况和实时路况等因素。

综上所述，最短路问题在许多实际案例中都有应用。

无论是导航系统、物流配送、电信网络、交通规划还是谷歌地图等，都需要计算出最短路径以满足需求。

因此，研究和解决最短路问题在实际应用中具有重要意义。

由三村最短路问题两个解法引发的推广

由三村最短路问题两个解法引发的推广

由三村最短路问题两个解法引发的推广背景在计算机科学中，最短路算法是一个基本的算法。

计算机科学的研究者一直在寻找更快、更有效的算法来解决这个问题。

因为最短路问题在许多实际应用程序中都是必须解决的问题。

其中一个最著名的应用是导航问题。

在最短路算法中，三村最短路问题是其中一个比较有名的问题。

三村最短路问题是指，在一个由三个节点组成的图中，寻找从第一个节点到第三个节点的最短路径。

不过，这个问题也可以扩展到多个节点的情况。

在这个问题中，我们需要找到一个算法，去计算每一个节点之间的距离，然后找到从起点到终点的最短路径。

这个问题在实际应用中是非常有用的，比如说在导航系统中，起点是你的当前位置，终点是你要到达的目的地。

解法一：Dijkstra算法Dijkstra算法是一个比较有名的最短路算法。

它是由荷兰计算机科学家Edsger Wybe Dijkstra在1956年发明的。

Dijkstra算法的核心是一个图中的顶点集合，被划分为两个部分：一个是已找到最短路径的顶点集合；另一个是未找到最短路径的顶点集合。

算法的步骤如下：1.初始化：将起点标记为已访问，并且将起点到起点的距离设为0，同时把起点的所有邻居节点加入未访问节点集合中。

2.遍历：对于所有的未访问节点中，选择当前距离起点最近的节点进行访问。

3.更新：对于已访问节点的邻居节点，更新它们到起点的距离，如果更新后的距离小于原来的距离，则更新邻居节点的距离（注意这里只会更新未访问节点的距离）。

如果更新了距离，则更新邻居节点到起点的路线。

4.重复步骤2和3直到访问完所有未访问节点或到达终点。

使用Dijkstra算法求解三村最短路问题，只需要按照上述步骤进行即可。

解法二：Floyd算法Floyd算法是另外一种比较有名的最短路算法，它是由Robert W. Floyd在1962年发明的。

Floyd算法的思路是一个动态规划算法，它通过中转点进行路径优化，最终得出最短路径。

因为它是一个动态规划算法，所以它的时间复杂度比较高，但是在实际应用中，还是被广泛采用的。

最短路问题专题

最短路问题专题
Step1：如果Si=V，算法终止，否则转入step2； Step2：考察每个使(vk,vj) ∈ A且vj不属于Si的点vj。如果T(vj)>P(vk)+wkj，则把T(vj) 修改为P(vk)+wkj，把 λ(vj)修改为k，否则转入step3；
Step3：令T(vji)=min{T(vj)| vj不属于Si}。如果T(vji)<+∞ ，则把vji的 T标号变为P标号，
令Si+1=Si ∪{vji}，k=ji，i=i+1，转入step1.
Matlab程序（见附件）
2 算法介绍-floyd算法

算法步骤：
Step1：输入图G的权矩阵W，对所有i，j，有dij=wij，k=1；
Step2：更新dij，对所有i，j，若dij>dik+dkj，则令dij=dik+dkj；
由此可以看出，算法的时间与随问题规模增大呈指数增长，所以最 短路算法不适合大规模配送问题求解。
考虑经过2点的Matlab程序（见附件）
3 应用举例
3.3 多目标运输问题
求次短路 Matlab程序
参考文献： 多目标最短路模型及算法，西南交通大学大学学报
最短路问题算法及应用
主要内容
1 问题描述 2 算法介绍
2.1 dijkstra算法 2.2 floyd算法
3 应用举例
3.1 物流中心选址 3.2 物流配送问题 3.3 多目标运输问题
1 问题描述
ቤተ መጻሕፍቲ ባይዱ
定义1 对简单图G的每一边e赋予一个实数，记为w(e)，称为边e的 权，而每边都赋予权的图称为赋权图。 定义2 (u,v)-路的边权之和称为该路的长，而u,v间路长达到最小的 路称顶点u和v的最短路。 在给定赋权图G中，求两个互异顶点间的最短路，简记为最短路问题。

最短路问题

最短路问题

v6
9
7
4
1 1 1
1 2 2
1 2 3
1 2 3
1 2 3
1 2
3
10 8
8 6
9
7
5 3 4
0 4 3
4 0 1
3
1
0
1 11
2 2 2
3 3 3
4 4 4
4 5 5
4
5 6
由于D(2) =D(3)，故D(3)中的元素就是vi到vj的 最短距离,D(3)称为最短距离矩阵。
1 1 2 2 3
到其他不直接邻接的节点的最短 距离不会发ห้องสมุดไป่ตู้变化。
②在v1到所有其他节点的最短距离中选择最小的距 离，找到节点 vk，使下式满足：
求 min{T (v j )}
vk
满足
T (vk
)
min{T
v jS
(v
j
)}
令：P(vk ) T (vk )
比较v1到所有其它节点的最短距离，找到 节点vk,并将最小的距离记录在P(vk)中。
的最短路。
（1）使用条件—没有负回路
（2）步骤：
①
令
d 1 j
w1 j，j
2,3,, N，其中
w1 j为起点v1
到 v j 的弧（v1, v j ）的权；
②用下列递推公式进行迭代：
d d k min
j
i
k 1
j
wij
j 2,3,, N
其中，
d k j
表示从起点 v1 到点 v j 走k步
的最短距离；
一、问题的提法及应用背景
（1）问题的提法——寻求网络中两点间 的最短路就是寻求连接这两个点的边的 总权数为最小的通路。（注意：在有向 图中，通路——开的初等链中所有的弧 应是首尾相连的。）

Excel 财务应用 最短路问题

Excel 财务应用 最短路问题

Excel 财务应用 最短路问题在网络优化问题中，许多问题都可以使用最短路优化的模型解决问题，如设备更新、管道铺设、线路安排和厂区布局等。

本节就以铺设管道为例，介绍如何利用规划求解，解决最短路问题。

某个新建住宅小区要从A 点到F 点铺设供水管道，中间经过B 、C 、D 、E 点，要求水源与各点相通，而且各点到水源间的路径最短，该管道各点之间的距离如图9-69所示。

求从A 点到F 点铺设管道的最短路径。

图9-69 各点之间的距离根据已知条件，在Excel 工作表中，输入相关数据，创建该问题的规划求解模型，如图9-70所示。

图9-70 创建求解模型 在创建该模型时，可以将出发地看成供应量为1的供应点，目的地为需求量为1的点，网络中其他点的净流量为0，并将各点之间的距离看作成本，即可将该问题转化为一个特殊的最小费用流问题。

接下来，计算各节点的净流量。

选择节点A 净流量所对应的单元格，即F14单元格，在【编辑栏】中，输入“=SUMIF(A14:A28,E14,C14:C28)-SUMIF(B14:B28,E14,C14:C28)”公式，即可计算该节点的净流量，如图9-71所示。

再使用相同的方法计算其他节点的净流量。

图9-71节点A 的净流量选择最短总距离所对应的单元格，即G27单元格，在【编辑栏】中，输入“=SUMPRO 已知条件输入DUCT(C14:C28,D14:D28)”公式，即可得到最短总距离的值，如图9-72所示。

输入图9-72 计算最短总距离然后，再次选择G27单元格，单击【规划求解】按钮，在【规划求解参数】对话框中，选择【最小值】单选按钮，设置可变单元格的数据区域，并添加“$F$14:$F$19=$H$14:$H$1 9”约束，如图9-73所示。

设置图9-73 设置规划求解参数最后，单击【求解】按钮，保留规划求解结果之后，即可得出该问题的最优解，如图9 -74所示。

求解结果图9-74 规划求解结果由规划求解结果可以得出结论：流量值为1的节点代表最短路径上的两个节点，流量值为0则表示不经过这两个节点。

数学建模-最短路问题

数学建模-最短路问题

，其中
d (2) ij

min{di(j1)
,
d (1) i2

d
(1) 2j
}
d
(2) ij
是从
v
i
到
v
j
的只允许以
v
1
、
v 2 作为中间点的路径中最短路的长度．
…
（
）D(ν)=
(d
( ij
)
)

，其中 di(j )
min{di(j 1) , di( 1)
d(j 1)}
0

S(v1)=10, S(v2)=7, S(v3)=6, S(v4)=8.5, S(v5)=7, S(v6)=7, S(v7)=8.5
S(v3)=6,故应将消防站设在v3处.
返回
选址问题--重心问题
例 3 某矿区有 7 个矿点，如图所示．已知各矿点每天的产矿量
为 q(v j ) （标在图的各顶点上）．现要从这 7 个矿点选一个来建造矿
图 论 复习
一、 图 的 概 念
二、 图 的 表 示 1． 关联矩阵 2． 邻接矩阵
图的定义
关联矩阵
对无向图Ｇ，其关联矩阵Ｍ＝ (mij ) ，其中：
1 mij 0
若vi与e
相关联
j
若vi与e
不关联
j
对有向图Ｇ，其关联矩阵Ｍ＝ (mij ) ，其中：
1 mij 1
)
,
i=1,2,3,4,5}∪{
(
X (k ir
)
,
X
(k 1) i 1,r
)
,i=1,2,3,4,5;k=1,2,i-1}
若第 i 年初作了决策 X i 后，第 i+1 年初可以作决策 X i1 ，则顶点 X i 与 X i1 之间有弧( X i , X i1 )，其权 W( X i , X i1 )代表第 i 年初到第 i+1 年

解最短路径问题的两种方法及其应用

解最短路径问题的两种方法及其应用

解最短路径问题的两种方法及其应用
最短路径问题是指在一张带权图中找到两个节点之间最短的路径。

最短路径问题是许多计算机科学和应用领域中的一个基本问题。

以下是解决这个问题的两种方法：
1. Dijkstra算法：Dijkstra算法是解决最短路径问题的一种
基本算法，它是基于贪心思想的。

该算法首先确定起始点到其他节
点的距离（记为d），然后不断扩大已确定最短距离的节点集，直
到覆盖所有节点。

Dijkstra算法适用于单源最短路径，即从一个节
点到所有其他节点的最短路径。

2. Floyd算法：Floyd算法也是一种经典的解决最短路径问题
的算法，它是一个动态规划算法。

该算法利用动态规划的思想，通
过比较任意两个节点之间经过第三点（中转点）的路径长度，更新
路径长度。

Floyd算法适用于多源最短路径，即从任意两个节点之
间的最短路径。

这两种算法可广泛应用于各种计算机科学和应用领域，如网页
排名算法、图像处理、计算机网络等。

在实际应用中，我们需要根
据实际问题的特点，选择最适合的算法。

多源最短路方案

多源最短路方案

多源最短路方案介绍在图论中，最短路问题是一个经典的问题，它的目标是在一个加权图中找到两点之间的最短路径。

然而，在实际应用中，我们有时需要寻找多个源点到其他所有点的最短路径。

这个问题被称为多源最短路问题。

本文将介绍多源最短路问题的定义、应用和求解方法。

定义多源最短路问题是指在一个加权有向图中，给定多个源点，求每个源点到其他所有点的最短路径。

不同于单源最短路问题，多源最短路问题要求从多个源点同时开始进行计算，并得到每个源点到其他所有点的最短路径。

应用多源最短路问题广泛应用于各个领域，具有很高的实际价值。

交通规划在城市交通规划中，多源最短路方案可以帮助确定最佳的交通路线。

通过计算多个起点到所有终点的最短路径，可以提供给交通规划者关于交通流量和交通拥堵情况的实时信息，从而优化交通路线，减少拥堵，提高交通效率。

网络通信在计算机网络领域，多源最短路方案可以用于路由算法的设计。

通过计算多个源点到所有节点的最短路径，可以选择最优的路由路径，提高网络的传输效率和可靠性。

物流配送在物流配送领域，多源最短路方案可以帮助确定最短的配送路径。

通过计算多个起点到所有终点的最短路径，可以制定出最优的物流配送方案，降低成本，提高配送效率。

求解方法多源最短路问题可以使用多种方法求解，其中最常用的方法包括Floyd-Warshall 算法和多源Dijkstra算法。

Floyd-Warshall算法Floyd-Warshall算法是一种经典的动态规划算法，用于解决所有点对最短路径问题。

该算法通过一个二维数组来存储每对节点之间的最短路径长度，然后通过动态规划的方法逐步更新这个数组，最终得到所有点对的最短路径。

Floyd-Warshall 算法的时间复杂度为O(V^3)，其中V是图中节点的数量。

算法步骤：1.初始化一个二维数组dist，用于存储每对节点之间的最短路径长度。

2.将dist数组初始化为图中的边权值矩阵。

3.对于每一个中间节点k，遍历所有的节点i和节点j，如果dist[i][j]大于dist[i][k]+dist[k][j]，则更新dist[i][j]为dist[i][k]+dist[k][j]。

MATLAB编程：最短路问题

MATLAB编程：最短路问题
（ 2 ） 更 新 l ( v ) 、 z ( v ) ： v S V \ S ,若 l ( v ) > l ( u ) W ( u , v )
z 则 令 l(v ) = l(u ) W (u , v ) , (v ) = u
（ 3） 设 v 是 使 l(v ) 取 最 小 值 的 S
定 义 ３ （ １ ） 设 P (u ,v)是 赋 权 图 G 中 从 u 到 v 的 路 径 ， 则 称 w(P)
e E ( P )
w (e) 为 路 径
P 的权．
(2 )
在赋权图 G 中，从顶点 u 到顶点 v 的具有最小权的路
P (u , v ) ， 称 为 u 到 v 的 最 短 路 ．
u2
u 6
6
u5
图 G 的 边 为 边 集 的 图 G 的 子 图 ， 称 为 G 的 由 V 1 导 出 的 子 图 ， 记 为 G[V 1 ]. (3)设 E 1 E ,且 E 1 ,以 E 1 为 边 集 ,E 1 的 端 点 集 为 顶 点 集 的 图 G 的 子 图 , 称 为 G 的 由 E 1 导 出 的 子 图 ,记 为 G[E 1 ].
返回
邻接矩阵
对 无 向 图 Ｇ ， 其 邻 接 矩 阵 A ( a ij ) ， 其 中 ：
a ij
1 0
若 v i 与 v j 相邻 若 v i 与 v j 不相邻
v1 A= 0 1 0 1 v2 1 0 1 1 0 1 0 1
注：假设图为简单图
返回
顶点的次数
定义 （１）在无向图中，与顶点 v 关联的边的 数目（环 算两次） 称 为 v 的 次 数 ， 记 为 d (v)． （２）在有向图中，从顶点 v 引出的边的数目称为 v 的出度， 记 为 d + ( v)， 从 顶 点 v 引 入 的 边 的 数 目 称 为 的 入 度 ， 记 为 d - (v)， d ( v)= d + ( v)+ d - ( v) 称 为 v 的 次 数 ．

最短路算法的应用

最短路算法的应用

最短路算法的应用最短路径算法的应用最短路径算法（Shortest Path Algorithm）是图论中的经典问题，其目标是在一个加权有向图或无向图中找到两个顶点之间的最短路径。

最短路径算法在现实生活中有着广泛的应用，包括交通导航、网络路由、物流运输等领域。

本文将详细介绍最短路径算法的原理及其应用。

一、最短路径算法的原理最短路径算法的核心思想是通过遍历图中的节点，并计算出每个节点到起始节点的最短路径值（即距离）。

最短路径算法主要有以下两种经典算法：1. 迪杰斯特拉算法（Dijkstra's Algorithm）：迪杰斯特拉算法用于求解单源最短路径问题，即给定一个起始节点，计算其到图中所有其他节点的最短路径。

该算法的步骤如下：（1）初始化：设置起始节点的最短路径值为0，其他节点的最短路径值为无穷大。

（2）选择最短路径值最小的节点，并将其标记为已访问。

（3）更新相邻节点的最短路径值：对于当前节点的所有相邻节点，通过比较经过当前节点的路径长度与已记录的最短路径值，更新最短路径值。

（4）重复步骤（2）和（3），直到所有节点都被标记为已访问。

（5）得到起始节点到图中其他节点的最短路径值。

2. 贝尔曼-福特算法（Bellman-Ford Algorithm）：贝尔曼-福特算法用于求解任意两个节点之间的最短路径，可以处理存在负权边的图。

该算法的步骤如下：（1）初始化：设置起始节点的最短路径值为0，其他节点的最短路径值为无穷大。

（2）对所有边进行松弛操作：遍历图中的所有边，通过比较经过当前边的路径长度与已记录的最短路径值，更新最短路径值。

（3）重复步骤（2）|V|-1次（其中|V|为图中节点的个数），以保证所有节点的最短路径值被正确计算。

（4）检测是否存在负权回路：再次遍历图中的所有边，如果经过某条边的路径长度仍然可以被缩短，则说明图中存在负权回路，无法得到最短路径。

（5）得到任意两个节点之间的最短路径值。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
这样每一次迭代,得到 到一点 的最短距离,重复上述过程直到 。
Floyd算法的基本原理和实现方法为:如果一个矩阵 其中 表示 与 间的距离,若 与 间无路可通,则 为无穷大。 与 间的最短距离存在经过 与 间的 和不经过 两种情况,所以可以令 ,n(n为节点数)。检查 与 的值,在此, 与 分别为目前所知的 到 与 到 的最短距离,因此, 就是 到 经过 的最短距离。所以,若有 ,就表示从 出发经 再到 的距离要比原来的 到 距离短,自然把 到 的 重写成 。每当一个 搜索完, 就是目前 到 的最短距离。重复这一过程,最后当查完所有 时, 就为 到 的最短距离。
3最短路的应用
3.1在运输网络中的应用④
设6个城市 之间的一个公路网(图1)每条公路为图中的边,边上的权数表示该段公路的长度(单位:百公里),设你处在城市 ,那么从 到 应选择哪一路径使你的费用最省。
解:首先设每百公里所用费用相同,求 到 的费用最少,既求 到 的最短路线。为了方便计算,先作出该网络的距离矩阵,如下:
最短路径算法的选择与实现是通道路线设计的基础,最短路径算法是计算机科学与地理信息科学等领域的研究热点,很多网络相关问题均可纳入最短路径问题的范畴之中。经典的图论与不断发展完善的计算机数据结构及算法的有效结合使得新的最短路径算法不断涌现。
2最短路
2.1最短路的定义
对最短路问题的研究早在上个世纪60年代以前就卓有成效了,其中对赋权图 的有效算法是由荷兰著名计算机专家E.W.Dijkstra在1959年首次提出的,该算法能够解决两指定点间的最短路,也可以求解图G中一特定点到其它各顶点的最短路。后来海斯在Dijkstra算法的基础之上提出了海斯算法。但这两种算法都不能解决含有负权的图的最短路问题。因此由Ford提出了Ford算法,它能有效地解决含有负权的最短路问题。但在现实生活中,我们所遇到的问题大都不含负权,所以我们在 的情况下选择Dijkstra算法。
路线优化技术通常采用图论中的“图”来表示路网,船舶通道路网与图论的路网对应关系为:结点———通道的交叉口或断头路的终点;边———两结点之间的路段称为边,若规定了路段的方向,则称为弧;边(弧)的权———路段某个或某些特征属性的量化表示。
路权的标定决定了最短的路径搜索依据,也就是搜索指标。根据不同的最优目标,可以选择不同的路段属性。由于舰船上除了平面上的通道之外还有垂直方向的楼梯(或直梯),如果以最短路程距离作为优化目标,路线的效率未必最高(距离最短未必耗时最少)。所以,以最短行程时间作为优化的目标,道路权重即为各路段的平均行程时间。
定义①1若图G=G(V,E)中各边e都赋有一个实数W(e),称为边e的权,则称这种图为赋权图,记为G=G(V,E,W)。
定义②2若图G=G(V,E)是赋权图且 , ,若u是 到 的路 的权,则称 为 的长,长最小的 到 的路 称为最短路。
若要找出从 到 的通路 ,使全长最短,即 。
2.2最短路问题算法的基本思想及基本步骤
在求解网络图上节点间最短路径的方法中,目前国内外一致公认的较好算法有迪杰斯特拉(Dijkstra)及弗罗伊德(Floyd)算法。这两种算法中,网络被抽象为一个图论中定义的有向或无向图,并利用图的节点邻接矩阵记录点间的关联信息。在进行图的遍历以搜索最短路径时,以该矩阵为基础不断进行目标值的最小性判别,直到获得最后的优化路径。
Dijkstra算法基本步骤③：
令：
并令：
Байду номын сангаас1、对 ，求 。
2、求 得 ，使 =
令
3、若 则已找到 到 的最短路距离 ，否则令 从 中删去 转1
这样经过有限次迭代则可以求出 到 的最短路线，可以用一个流程图来表示：
第一步先取 意即 到 的距离为0,而 是对 所赋的初值。
第二步利用 已知,根据 对 进行修正。
(0)设 ,
(1)第一次迭代
①计算 如下
②取 ,令
③由于 ,令 转(1)
第二次迭代:
①算 如下
②取 令
③由于 ,令 转(1)
第三次迭代:
①算 如下
②取
③由于 ,令 转(1)
第四次迭代:
①算 如下
②取
③由于 ,令 转(1)
第五次迭代:
①算 如下
②由于 。因此已找到 到 的最短距离为12。计算结束。
找最短路线:逆向追踪得
第三步对所有修正后的 求出其最小者 。其对应的点 是 所能一步到达的点 中最近的一个,由于所有 。因此任何从其它点 中转而到达 的通路上的距离都大于 直接到 的距离 ,因此 就是 到 的最短距离,所以在算法中令 并从s中删去 ,若k=n则 就是 到 的最短路线,计算结束。否则令 回到第二步,继续运算,直到k=n为止。
最短距离为12,即从城市 到城市 的距离最短,即费用最省。
3.2在舰船通道路线设计中的应用⑤
利用图论的经典理论和人群流量理论研究舰船人员通道路线的优化设计及最优线路选择。首先介绍图论相关理论,对船舶通道进行路网抽象,建立网络图,然后根据人群流动的相关理论,选取不同拥挤情况下的人员移动速度,从而确定各条路段(包括楼梯)的行程时间。以行程时间作为通道网络的路权，得出路阻矩阵以选择一对起点/终点的最短时间路线为目标,建立最短路径问题的数学模型,利用经典的Floyd算法确定最短路径。将此方法应用于某舰艇多层甲板的通道网络中,计算结果并进行讨论,最后在此研究的基础上对通道设计相关问题的深化和拓展进行了探讨和总结,并提出设想。
最短路问题及其应用
顾碧芬06200103
摘要：主要介绍最短路的两种算法，迪杰斯特拉(Dijkstra)及弗罗伊德(Floyd)算法。以及这两种算法在实际问题中的应用和比较。
1引言
最短路问题是图论理论的一个经典问题。寻找最短路径就是在指定网络中两结点间找一条距离最小的路。最短路不仅仅指一般地理意义上的距离最短,还可以引申到其它的度量,如时间、费用、线路容量等。
Dijkstra算法是图论中确定最短路的基本方法,也是其它算法的基础。为了求出赋权图中任意两结点之间的最短路径,通常采用两种方法。一种方法是每次以一个结点为源点,重复执行Dijkstra算法n次。另一种方法是由Floyd于1962年提出的Floyd算法,其时间复杂度为 ,虽然与重复执行Dijkstra算法n次的时间复杂度相同,但其形式上略为简单,且实际运算效果要好于前者。