电磁场与电磁波(第三章)
- 格式:doc
- 大小:104.00 KB
- 文档页数:4
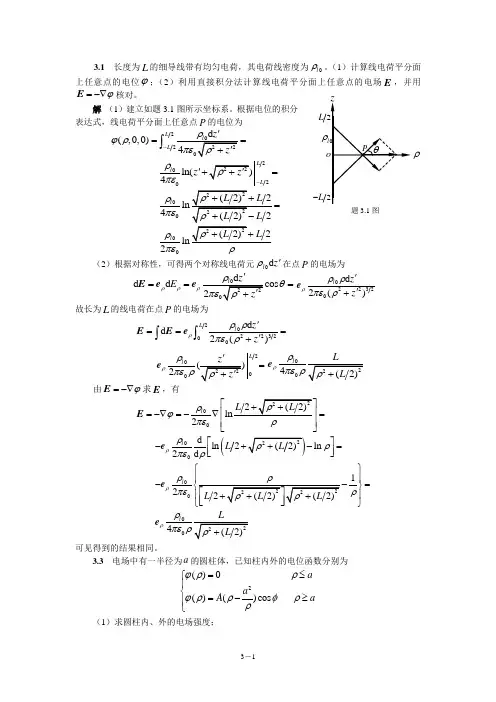
3.1 长度为L 的细导线带有均匀电荷,其电荷线密度为0l ρ。
(1)计算线电荷平分面上任意点的电位ϕ;(2)利用直接积分法计算线电荷平分面上任意点的电场E ,并用ϕ=-∇E 核对。
解 (1)建立如题3.1图所示坐标系。
根据电位的积分表达式,线电荷平分面上任意点P 的电位为2(,0,0)L L ϕρ-==⎰2ln(4L l L z ρπε-'+=04l ρπε=02l ρπε (2)根据对称性,可得两个对称线电荷元z l 'd 0ρ在点P 的电场为d d E ρρρθ'===Ee e 022320d 2()l z z ρρρπερ''+e故长为L 的线电荷在点P 的电场为2022320d d 2()L l z z ρρρπερ'==='+⎰⎰E E e20002L l ρρπερ'=e ρe 由ϕ=-∇E 求E ,有002l ρϕπε⎡⎢=-∇=-∇=⎢⎥⎣⎦E(00d ln 2ln 2d l L ρρρπερ⎡⎤-+-=⎢⎥⎣⎦e0012l ρρπερ⎧⎫⎪--=⎬⎪⎭e ρe可见得到的结果相同。
3.3 电场中有一半径为a 的圆柱体,已知柱内外的电位函数分别为2()0()()cos a a A aϕρρϕρρφρρ=≤⎧⎪⎨=-≥⎪⎩(1)求圆柱内、外的电场强度;L L -ρρ题3.1图(2)这个圆柱是什么材料制成的?表面有电荷分布吗?试求之。
解 (1)由ϕ=-∇E ,可得到a ρ<时, 0ϕ=-∇=Ea ρ>时, ϕ=-∇=E 22[()cos ][()cos ]a a A A ρφρφρφρρρφρ∂∂----=∂∂e e 2222(1)cos (1)sin a a A A ρφφφρρ-++-e e(2)该圆柱体为等位体,所以是由导体制成的,其表面有电荷分布,电荷面密度为0002cos S n a a A ρρρρεεεφ=====-e E e E3.4 已知0>y的空间中没有电荷,下列几个函数中哪些是可能的电位的解? (1)cosh y e x -; (2)x e y cos -;(3)cos sin e x x (4)z y x sin sin sin 。



第三章 静电场3-1 已知在直角坐标系中四个点电荷分布如习题图3-1所示,试求电位为零的平面。
解 已知点电荷q 的电位为rq 4πεϕ=,令)0,1,0(1q q -=,)0,1,3(2q q +=,)0,0,1(3q q -=,)0,0,0(4q q +=,那么,图中4个点电荷共同产生的电位应为∑=414ii r q πεϕ令0=ϕ,得 0 4 4 4 44321=+-+-r qr q r q r q πεπεπεπε 由4个点电荷的分布位置可见,对于x =1.5cm 的平面上任一点,4321 ,r r r r ==,因此合成电位为零。
同理,对于x =0.5cm 的平面上任一点,3241 ,r r r r ==,因此合成电位也为零。
所以,x =1.5cm 及x =0.5cm 两个平面的电位为零。
3-2 试证当点电荷q 位于无限大的导体平面附近时,导体表面上总感应电荷等于)(q -。
证明 建立圆柱坐标,令导体表面位于xy 平面,点电荷距离导体表面的高度为h ,如图3-2所示。
那么,根据镜像法,上半空间的电场强度为32023101 4 4r q r q πεπεr r E -=X 习题图3-1(r , z )习题图3-2电通密度为)(43223110r r q r r E D -==πε 式中 232231])([h z r r -+=; 232232])([h z r r ++=那么,⎥⎥⎥⎦⎤⎪⎪⎪⎭⎫ ⎝⎛+++-++-+⎢⎢⎢⎣⎡⎪⎪⎪⎭⎫ ⎝⎛++--+=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++++--+-+=z z zh z r hz h z r h z h z r r h z r r q h z r h z r h z r h z r q e e e e e e D r r r 232223222322232223222322])([])([ ])([])([4 ])([)(])([)(4ππ 已知导体表面上电荷的面密度n s D =ρ,所以导体表面的感应电荷为2322232223220)(2][][4h r qh h r h h r h q D z zs +-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++-+-===ππρ 则总的感应电荷为q h r r r qh r r S q s ss -=+-===⎰⎰⎰∞∞2322)(d d 2d 'πρρ3-3 根据镜像法,说明为什么只有当劈形导体的夹角为π的整数分之一时,镜像法才是有效的?当点电荷位于两块无限大平行导体板之间时,是否也可采用镜像法求解。



第3章习题3-1 半径为的薄圆盘上电荷面密度为s ρ,绕其圆弧轴线以角频率旋转形成电流,求电流面密度。
解:圆盘以角频率旋转,圆盘上半径为r 处的速度为r ω,因此电流面密度为ϕωρρˆr v J s s s ==3-2 在铜中,每立方米体积中大约有28105.8⨯个自由电子。
如果铜线的横截面为210cm ,电流为A 1500。
计算 1) 电流密度;2) 电子的平均漂移速度; 解:1)电流密度m A S I J /105.11010150064⨯=⨯==- 2) 电子的平均漂移速度 v J ρ=,3102819/1036.1105.8106.1m C eN ⨯=⨯⨯⨯==-ρs m J v /101.11036.1105.14106-⨯=⨯⨯==ρ 3-3 一宽度为cm 30传输带上电荷均匀分布,以速度s m /20匀速运动,形成的电流,对应的电流强度为A μ50,计算传输带上的电荷面密度。
解:电流面密度为m A L I J S /7.1663.050μ===因为 v J S S ρ= 所以 2/33.8207.166m C v J S S μρ=== 3-4 如果ρ是运动电荷密度,U是运动电荷的平均运动速度,证明:0=∂∂+∇⋅+⋅∇tU U ρρρ证:如果ρ是运动电荷密度,U是运动电荷的平均运动速度,则电流密度为U J ρ=代入电荷守恒定律tJ ∂∂-=⋅∇ρ得0=∂∂+∇⋅+⋅∇t U U ρρρ3-5 由m S /1012.17⨯=σ的铁制作的圆锥台,高为m 2,两端面的半径分别为cm 10和cm 12。
求两端面之间的电阻。
解:用两种方法(1)如题图3.5所示⎰⎰==2122)(tan zz lz dzS dl R ασπσ)11()(tan 1212z z -=ασπ 01.0202.0tan ==α题3.5图m r z .1001.0/1.0tan /11===α,m r z 1201.0/12.0tan /22===αΩ⨯=-⨯⨯⨯=-=--647212107.4)121101(101012.11)11()(tan 1πασπz z R (2)设流过的电流为I ,电流密度为2rI S I J π==电场强度为 2r IJ E πσσ== 电压为 dz z IEdz V z z z z ⎰⎰==21212)tan (σαπ ⎰==2122)(tan zz zdz I V R απσΩ⨯=-6107.4 3-6 在两种媒质分界面上,媒质1的参数为2,/10011==r m S εσ,电流密度的大小为2/50m A ,方向和界面法向的夹角为030;媒质2的参数为4,/1022==r m S εσ。


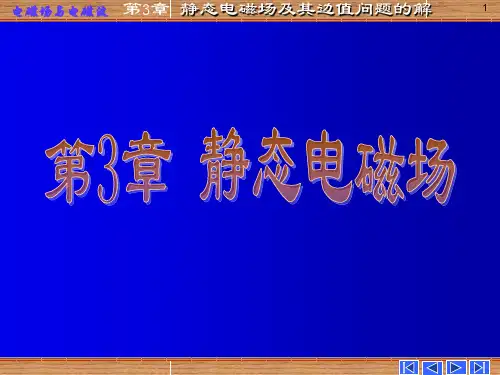

第三章习题解答3.1 真空中半径为a的一个球面,球的两极点处分别设置点电荷q和-q,试计算球赤道平面上电通密度的通量Φ(如题3.1图所示)。
解由点电荷q和-q共同产生的电通密度为qR+R-D=[3-3]=4πRR+-q4π{err+ez(z-a)[r+(z-a)]2232-err+ez(z+a)[r+(z+a)]2232Φ=则球赤道平面上电通密度的通量⎰D dS=⎰D eSSzz=0dS=]2πrdr=q4πa题3.1 图⎰[02(-a)(r+a)qaa-a(r+a)2232(r+a)=0-1)q=-0.293q3.2 1911年卢瑟福在实验中使用的是半径为ra的球体原子模型,其球体内均匀分布有总电荷量为-Ze的电子云,在球心有一正电荷Ze(Z是原子序数,e是质子电荷量),通Ze⎛1r⎫过实验得到球体内的电通量密度表达式为D0=er 2-3⎪,试证明之。
4π⎝rra⎭Ze解位于球心的正电荷Ze球体内产生的电通量密度为 D1=er 24πrZe3Ze=-原子内电子云的电荷体密度为ρ=-334πra4πra电子云在原子内产生的电通量密度则为D2=erρ4πr4πr32=-erZer4πra3题3. 3图(a)故原子内总的电通量密度为 D=D1+D2=er 2-3⎪4π⎝rra⎭33.3 电荷均匀分布于两圆柱面间的区域中,体密度为ρ0Cm, 两圆柱面半径分别为a和b,轴线相距为c(c<b-a),如题3.3图(a)所示。
求空间各部分的电场。
解由于两圆柱面间的电荷不是轴对称分布,不能直接用高斯定律求解。
但可把半径为a的小圆柱面内看作同时具有体密度分别为±ρ0的两种电荷分布,这样在半径为b的整个圆柱体内具有体密度为ρ0的均匀电荷分布,而在半径为a的整个圆柱体内则具有体密度为-ρ0的均匀电荷分布,如题3.3图(b)所示。
空间任一点的电场是这两种电荷所产生的电场的叠加。
在r>b区域中,由高斯定律⎰E dS=Sqε022,可求得大、小圆柱中的正、负电荷在点P E1'=er'-πaρ02πε0r'2产生的电场分别为 E1=erπbρ02πε0r2=ρ0br2ε0r=-ρ0ar'22ε0r'2=+题3. 3图(b)点P处总的电场为 E=E1+E1'= ρ2ε0(brr-2r')在r<b且r'>a区域中,同理可求得大、小圆柱中的正、负电荷在点P产生的电场分别为E2=erπrρ2πε0r=ρr2ε0'=er' E2-πaρ2πε0r'=-ρar'2ε0r''=点P处总的电场为 E=E2+E2ρ02ε0(r-ar'r')在r'<a的空腔区域中,大、小圆柱中的正、负电荷在点P产生的电场分别为E3=erπrρ02πε0r=ρ0r2ε0'=er' E3-πr'ρ02πε0r'=-ρ0r'2ε0'=点P处总的电场为 E=E3+E3ρ0(r-r')=ρ02ε0c3.4 半径为a的球中充满密度ρ(r)的体电荷,已知电位移分布为⎧r3+Ar2⎪Dr=⎨a5+Aa4⎪2⎩r(r≤a)(r≥a)其中A为常数,试求电荷密度ρ(r)。
第3章习题
习题3.3
解:
(1) 由ϕ-∇=E
可得到 a <ρ时, 0=-∇=ϕE
a >ρ时, φρφρϕφρsin 1cos 12222⎪⎪⎭
⎫
⎝⎛-+⎪⎪⎭⎫ ⎝⎛+-=-∇=a A e a A e E
(2) 圆柱体为等位体且等于0,所以为导体制成,其电荷面密度为
φεεερρρρcos 2000A E
e E
e a
a
n s -=⋅=⋅===
习题3.5
证:
根据高斯定律q S d D S
=⋅⎰
,得
0R r <时。
ρππ344312
r D r =,则0
01113,3εερεερr r r
D E r D === 0R r >时。
ρππ3443022
R D r =,则203002
223023,3r R D E r
R D ερερ=== 则中心点的电位为
20
0200
203
020
13633)0(0
ερεερερεερϕR
R dr r
R dr r dr E dr E r R R R r R +=
+=+=⎰⎰
⎰⎰∞
∞
习题3.8
解:
根据高斯定律q S d D S
=⋅⎰
,得同轴线内、外导体间的电场强度为
περ
ρ2)(l q E =
内、外导体间的电压为
a
b q d q Ed U l b a
b
a
l ln 22περπερ
ρ=
==⎰⎰
则同轴线单位长度的电容为
)
/ln(2a b U q U Q C l πε
=
==
则同轴线单位长度的静电储能为
)/ln(422212122
2
a b q d q dV E W l b a l V e περπρπερεε=⎪⎪⎭
⎫ ⎝⎛==⎰⎰
习题3.11
解:
(1) 设同轴电缆中单位长度的径向电流为I ,电流密度
)(2c a I e J <<=ρπρ
ρ
介质中的电场
)(21
1
1b a I e J E <<==ρπρσσρ
)(22
2
2c b I e J E <<==ρπρσσρ
而
⎰
⎰+=
⋅+⋅=b
a
b a
b
c I a b I
d E d E U ln 2ln
221
210πσπσρρ )
/ln()/ln(2120
21b c a b U I σσσπσ+=
得到两种介质中的电流密度和电场强度分别为
[]
)()/ln()/ln(120
21c a b c a b U e J <<+=ρσσρσσρ
[])()/ln()/ln(120
21b a b c a b U e E <<+=ρσσρσρ
[]
)()/ln()/ln(120
12c b b c a b U e E <<+=ρσσρσρ
(2) 同轴电缆中单位长度的漏电阻为
2
11202)
/ln()/ln(σπσσσb c a b I U R +=
=
由静电比拟,可得同轴电缆中单位长度的电容
)
/ln()/ln(2122
1b c a b C εεεπε+=
习题3.19
解:
(1)同轴线的内外导体之间的磁场沿φ方向,根据两种磁介质的分界面上,磁场法向方向连续,则两种磁介质的磁感应强度B e B B B φ
===21,注意磁场强度21H H
=。
利用安培环路定律, 当a <ρ时,2
2002πρπμπρa
I B =
所以,)(22
00a a I
B <=
ρρπμ
当b a <<ρ时,I H H =+)(21πρ, 即,I B B =+
)(
2
2
1
1
μμπρ
所以,)()(2121b a I e B <<+=ρρ
μμπμμφ
同轴线中单位长度储存的磁场能量为
a
b I I d B d B d B W a b a b a m ln )(2162121221212
212002
2
12020μμπμμπμρ
πρμρπρμρπρμ++=
++=⎰⎰⎰
(2)由2
2
1LI W m =
,得到单位长度的自感为 a b
I
W L m ln )(82212102
μμπμμπμ++==。