空间弯管画法
- 格式:doc
- 大小:936.50 KB
- 文档页数:42
第十三章空间弯管作图法在锅炉的设计制造过程中,经常要涉及到大量空间弯管。
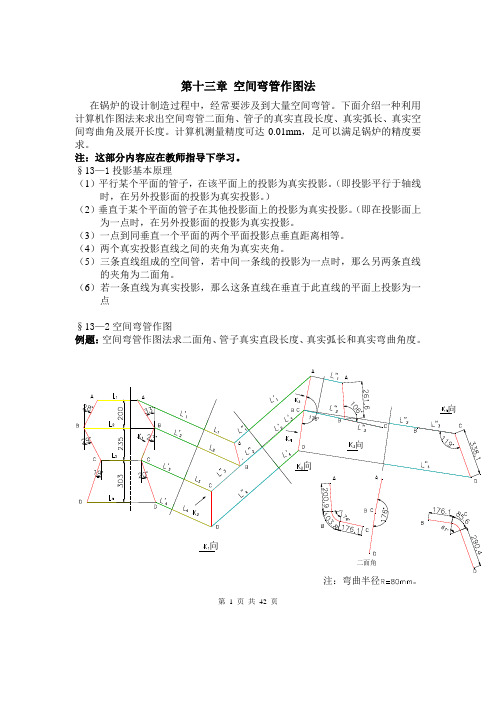
下面介绍一种利用计算机作图法来求出空间弯管二面角、管子的真实直段长度、真实弧长、真实空间弯曲角及展开长度。
计算机测量精度可达0.01mm,足可以满足锅炉的精度要求。
注:这部分内容应在教师指导下学习。
§13—1投影基本原理(1)平行某个平面的管子,在该平面上的投影为真实投影。
(即投影平行于轴线时,在另外投影面的投影为真实投影。
)(2)垂直于某个平面的管子在其他投影面上的投影为真实投影。
(即在投影面上为一点时,在另外投影面的投影为真实投影。
(3)一点到同垂直一个平面的两个平面投影点垂直距离相等。
(4)两个真实投影直线之间的夹角为真实夹角。
(5)三条直线组成的空间管,若中间一条线的投影为一点时,那么另两条直线的夹角为二面角。
(6)若一条直线为真实投影,那么这条直线在垂直于此直线的平面上投影为一点§13—2空间弯管作图例题:空间弯管作图法求二面角、管子真实直段长度、真实弧长和真实弯曲角度。
注:弯曲半径。
第 1 页共42 页§13—3练习题1.作图求真实弯曲角。
答案:直线真实长度: 真实角度:AB=84.34mm ∠ABC=150°BC=139.34mm ∠BCD=144°CD=117.11mm 二面角X=144.81°2.作图求真实弯曲角。
(答案:∠ABC=68.4°)3.作图求二面角、真实弯曲角。
(答案:二面角=112;∠ABC=110;∠BCD=97.7°)。
第 2 页共42 页4.作图求二面角,真实弯曲角。
)(答案:二面角=32.4°;∠CDE=96°;∠BCD=97.7°(答案:二面角=112;∠CDE=96;∠DEF=105°)学习方法及注意事项1,通过做例题掌握作图方法。
2,正确理解并掌握投影基本原理,能正确分析出哪条线是真实投影线和哪个角是真实投影角。


空间多角度弯管的展开料长度计算方法在工业生产中,空间多角度弯管是一种常见的构件。
由于其形状复杂,计算展开料长度成为一项关键任务。
本文将详细介绍空间多角度弯管的展开料长度计算方法,以帮助工程师和制造人员准确估算材料。
一、空间多角度弯管概述空间多角度弯管是指管道在空间内沿多个方向弯曲的构件。
这种构件广泛应用于航空航天、船舶、石油化工、建筑等领域。
由于其特殊的形状,使得展开料长度的计算相对复杂。
二、展开料长度计算方法1.图解法图解法是一种直观的计算方法,适用于简单空间多角度弯管。
具体步骤如下:(1)绘制空间多角度弯管的正投影图。
(2)将正投影图分解为若干个简单的直线段和曲线段。
(3)测量各段长度,并计算出展开料长度。
(4)考虑弯曲半径和角度对展开料长度的影响,进行修正。
2.数学解析法数学解析法适用于复杂空间多角度弯管的展开料长度计算。
具体步骤如下:(1)建立空间坐标系,确定弯管的几何参数。
(2)根据弯管的几何形状,列出曲线方程。
(3)求解曲线方程,得到展开料长度。
(4)考虑弯曲半径、角度等因素,对展开料长度进行修正。
3.计算机辅助设计(CAD)法随着计算机技术的发展,CAD法在空间多角度弯管展开料长度计算中得到了广泛应用。
具体步骤如下:(1)利用CAD软件绘制空间多角度弯管的三维模型。
(2)根据三维模型,自动生成展开图。
(3)利用CAD软件的测量功能,获取展开料长度。
(4)考虑弯曲半径、角度等因素,进行修正。
三、总结空间多角度弯管的展开料长度计算方法有多种,包括图解法、数学解析法和计算机辅助设计(CAD)法。
在实际应用中,可以根据具体情况选择合适的计算方法。
需要注意的是,计算过程中要充分考虑弯曲半径、角度等因素,以确保展开料长度的准确性。
通过以上介绍,希望对工程师和制造人员在空间多角度弯管展开料长度的计算方面有所帮助。



第十三章空间弯管作图法在锅炉的设计制造过程中,经常要涉及到大量空间弯管。
下面介绍一种利用计算机作图法来求出空间弯管二面角、管子的真实直段长度、真实弧长、真实空间弯曲角及展开长度。
计算机测量精度可达0.01mm,足可以满足锅炉的精度要求。
注:这部分内容应在教师指导下学习。
§13—1投影基本原理(1)平行某个平面的管子,在该平面上的投影为真实投影。
(即投影平行于轴线时,在另外投影面的投影为真实投影。
)(2)垂直于某个平面的管子在其他投影面上的投影为真实投影。
(即在投影面上为一点时,在另外投影面的投影为真实投影。
(3)一点到同垂直一个平面的两个平面投影点垂直距离相等。
(4)两个真实投影直线之间的夹角为真实夹角。
(5)三条直线组成的空间管,若中间一条线的投影为一点时,那么另两条直线的夹角为二面角。
(6)若一条直线为真实投影,那么这条直线在垂直于此直线的平面上投影为一点§13—2空间弯管作图例题:空间弯管作图法求二面角、管子真实直段长度、真实弧长和真实弯曲角度。
注:弯曲半径。
第 1 页共42 页§13—3练习题1.作图求真实弯曲角。
答案:直线真实长度: 真实角度:AB=84.34mm ∠ABC=150°BC=139.34mm ∠BCD=144°CD=117.11mm 二面角X=144.81°2.作图求真实弯曲角。
(答案:∠ABC=68.4°)3.作图求二面角、真实弯曲角。
(答案:二面角=112;∠ABC=110;∠BCD=97.7°)。
第 2 页共42 页4.作图求二面角,真实弯曲角。
)(答案:二面角=32.4°;∠CDE=96°;∠BCD=97.7°(答案:二面角=112;∠CDE=96;∠DEF=105°)学习方法及注意事项1,通过做例题掌握作图方法。
2,正确理解并掌握投影基本原理,能正确分析出哪条线是真实投影线和哪个角是真实投影角。
第1步做两条相互垂直的空间直线
第2步把两条相互垂直的空间
直线要联接的一端缩短1100
直线要联接的一端缩短1100后重新做一条200长的直线
第4步把刚才加长的直线端桥接起来
第5步把刚才桥接线插入点分成4等分,
第6步把刚才插入点用直线联接起来,
第7步把刚才联接直线分段做成管道
第8步把管道端面偏置210
第9步做偏置后的两个面做中分平面
第10步利用中分平面把管多余的部分分割掉。
第11步分割后把其余的隐藏起来,只剩要做图的一段。
第12步拉伸中间的直线成片体如图。
第13步片体加后与管道求差。
第14步转到钣金模块。
第15步转换成钣金。
第16步把管道展开,展开后转到建模模块。
第17步抽取等参数曲线。
第17步转到工程图模块,出图。
大功告成,你用过UG的应该不会有问题吧,如果搞不定我就没办法了,祝你好运!。
第十三章空间弯管作图法在锅炉的设计制造过程中,经常要涉及到大量空间弯管。
下面介绍一种利用计算机作图法来求出空间弯管二面角、管子的真实直段长度、真实弧长、真实空间弯曲角及展开长度。
计算机测量精度可达0.01mm,足可以满足锅炉的精度要求。
注:这部分内容应在教师指导下学习。
§13—1投影基本原理注:弯曲半径。
§13—3练习题1.作图求真实弯曲角。
2.3.4.作图求二面角,真实弯曲角。
(答案:二面角=32.4°;∠CDE=96°;∠BCD=97.7°)5,附:空间弯管练习题1~5的作图空间弯管练习题1计算方法。
此计算方法思路清晰,简单易懂,容易掌握,尤其借助计算机计算,即迅速又准确。
经过在工程上反复使用,实践表明此种计算方法准确无误。
欢迎广大读者参阅使用,如有错误和不当之处敬请批评指正。
注:一般采用两种方法来求:空间弯管二面角、管子的真实直段长度、真实弧长、真实空间弯曲角及展开长度。
用两种方法求出的结果完全相同时,表明结果正确。
否则,不是作图错误就是计算错误。
这样可以保证结果正确无误。
§14—1空间管计算(例题1)说明:通过具体例题,掌握计算方法。
1,二面角计算说明:此题图形为非标准图,作图求出标准图形(见上图)。
[A]投影[B]投影上图是通过作图求得的标准图(即保证主视图中间线段BC为真实投影),必须是标准图才行。
而且不同投影格式二面角计算公式不同。
(见下述)名称符号计算公式结果单位投影角β1注:角度符号为标准格式(见上图)。
0.40806 弧度β'10.76288 弧度α10.57858 弧度β20.74107 弧度β'2 1.09572 弧度α20.73304 弧度二面角分角X1 arctg(tgα1×cosβ1/SINβ'1)0.71462 弧度二面角分角X2 arctg(tgα2×cosβ2/SINβ'2)0.64158 弧度二面角θ(查表一)π-|X1-X2| 3.06855 弧度[A]投影[B]投影二面角θ异侧同侧X1+X2同侧异侧180-(X1+X2)同侧同侧|X1-X2|异侧异侧180-|X1-X2|求二面角的计算步骤①,通过作图求得的标准图(即保证主视图中间线段BC为真实投影);②,计算二面角分角X1、X2;③,查表一,找出计算二面角对应的公式,计算二面角。
2,空间弯曲角计算附注:空间角计算公式(将结果中符号代入具体角度便得结果)表1 第一类投影角ω注:角度符号为标准格式(见上图)。
弧度η弧度空间角αarc(cosω×cosη)弧度表2 第二类投影角φ注:角度符号为标准格式(见上图)。
弧度η弧度ω弧度中间参数角θarctg(tgω×cosφ)弧度中间参数角γφ+η弧度空间角αarc(cosθ×cosγ)弧度表3 第三类投影角φ注:角度符号为标准格式(见上弧度η图)。
弧度ω弧度中间参数角θarctg(tgω×cosφ)弧度中间参数角γ|φ-η|弧度空间角αarc(cosθ×cosγ)弧度表4 第四类投影角φ注:角度符号为标准格式(见上图)。
弧度η弧度ω弧度ε弧度中间参数角θarctg(tgω×cosφ)弧度中间参数角βarctg(tgε×cosη)弧度中间参数角γφ+η弧度空间角αarccos(cos θ×cosβ×cosγ-sinθ×sinβ)弧度表5 第五类投影角φ注:角度符号为标准格式(见上图)。
度η弧度ω弧度ε弧度中间参数角θarctg(tgω×cosφ)弧度中间参数角βarctg(tgε×cosη)弧度中间参数角γ|φ-η|弧度空间角αarccos(cos θ×cosβ×cosγ-sinθ×sinβ)弧度表6 第六类投影角φ注:角度符号为标准格式(见上图)。
弧度η弧度ω弧度ε弧度中间参数角θarctg(tgω×cosφ)弧度中间参数角βarctg(tgε×cosη)弧度中间参数角γφ+η弧度空间角αarccos(cos θ×cosβ×cosγ+sinθ×sinβ)弧度表7 第七类投影角φ注:角度符号为标准格式(见上图)。
弧度η弧度ω弧度ε弧度中间参数角θarctg(tgω×cosφ)弧度中间参数角βarctg(tgε×cosη)弧度中间参数角γ|φ-η|弧度空间角αarccos(cos θ×cosβ×cosγ+sinθ×sinβ)弧度投影角φ注:角度符号为标准格式(见上图)。
中心角计算采用的计算公式查附注:表1~表7。
0.48869 弧度η0.50615 弧度ω0.57596 弧度ε0.40143 弧度中间参数角θarctg(tgω×cosφ)0.52063 弧度中间参数角βarctg(tgε×cosη)0.35548 弧度中间参数角γφ+η0.99484 弧度ABC中心角α1arccos(cos θ×cosβ×cosγ-sinθ×sinβ)1.2976 弧度∠ABC180-α1×180/π105.65 度投影角φ注:角度符号为标准格式(见上0.50615 弧度η图)。
中心角计算采用的计算公式查附注:表1~表7。
0.33161 弧度ω0.40143 弧度ε0.34907 弧度中间参数角θarctg(tgω×cosφ)0.35548 弧度中间参数角βarctg(tgε×cosη)0.33145 弧度中间参数角γφ+η0.83776 弧度BCD中心角α1arccos(cos θ×cosβ×cosγ-sinθ×sinβ)1.07026 弧度∠BCD180-α1×180/π118.68 度空间弯曲角的计算步骤①,投影角的符号标为标准格式;②,查附注:表1~表7,找出中心角计算采用的计算公式;③,代入相应角度计算。
3,空间管AB,BC,CD实长计算投影角∠a注:角度符号为标准格式(见图一),以垂线为轴,顺时针为(+),逆时针为(-)。
并且保证必须是0.48869 弧度∠b-0.50615 弧度∠c此标准格式,否则此计算公式不0.33161 弧度适用。
∠d-0.57596 弧度∠e0.40143 弧度∠f-0.34907 弧度h1给定200.00 mmh2给定233.8 mmh3给定303.1 mm AB段长度L AB h1(1+tg2a+tg2d)0.5261.11 mm BC段长度L BC h2(1+tg2b+tg2e)0.5285.14 mm CD段长度L CD h3(1+tg2c+tg2f)0.5339.02 mm §14—2空间管计算演练题说明:演练题要求自己独立完成。
通过计算,检验是否掌握空间管计算的计算方法。
1,演练题一计算题1符合标准格式一,二面角计算名称符号计算结果单位投影角β1注:角度符号为标准格式(见上图)。
0.34907 弧度β'1 1.5708α1 1.5708 弧度β20.34907 弧度β'2 1.5708α20.40143 弧度二面角分角X1 arctg(tgα1×cosβ1/SINβ'1) 1.5708 弧度二面角分角X2 arctg(tgα2×cosβ2/SINβ'2)0.37954 弧度二面角θ(查表一)X1+X2 1.95033 弧度二面角θ180/π×(X1+X2)111.75 度二,空间弯曲角计算空间角∠ABC∠ABC为真实投影角110 度空间角α1180-∠ABC 70 度投影角ω注:角度符号为标准格式(见上图)。
中心角计算采用的计算公式查附注:表1~表7。
1.22173 弧度η 1.16937 弧度空间角α2arc(cosω×cosη) 1.43676 弧度空间角α2arc(cosω×cosη)×180/π82.32 度三,空间管AB,BC,CD实长计算投影角∠a注:角度符号为标准格式(见图一),以垂线为轴,顺时针为(+),逆时针为(-)。
并且保证必须是此标准格式,否则此计算公式不适用。
0 弧度∠b-1.22173 弧度∠c0 弧度∠d0 弧度∠e0 弧度∠f 1.16937 弧度h1给定149.25 mmh2给定54.69 mmh3给定140.8 mm AB段长度L AB h1(1+tg2a+tg2d)0.5149.25 mm BC段长度L BC h2(1+tg2b+tg2e)0.5159.90 mm CD段长度L CD h3(1+tg2c+tg2f)0.5360.35 mm计算题2是非标准格式,需变换成标准格式上图是通过作图求得的标准图,必须是标准格式才行。
不同投影格式计算公式不同。
一,二面角计算名称符号计算结果单位投影角β1注:角度符号为标准格式(见上图)。
0.40143 弧度β'1 1.5708 弧度α10.34907 弧度β20.40143 弧度β'2 1.5708 弧度α20.2618 弧度二面角分角X1 arctg(tgα1×cosβ1/SINβ'1)0.32328 弧度二面角分角X2 arctg(tgα2×cosβ2/SINβ'2)0.24182 弧度二面角θ(查表一)X1+X20.5651 弧度二面角θ180/π×(X1+X2)32.38 度二,空间弯曲角计算投影角ω注:角度符号为标准格式(见上图)。
中心角计算采用的计算公式查附注:表1~表7。
1.22173 弧度η 1.16937 弧度空间角α1arc(cosω×cosη) 1.43676 弧度空间角α1arc(cosω×cosη)×180/π82.32 度投影角ω注:角度符号为标准格式(见上图)。
中心角计算采用的计算公式查附注:表1~表7。
1.16937 弧度η 1.309 弧度空间角α2arc(cosω×cosη) 1.46949 弧度空间角α2arc(cosω×cosη)×180/π84.20 度三,空间管BC,CD,DE实长计算投影角∠a注:角度符号为标准格式(见图一),以垂线为轴,顺时针为(+),逆时针为(-)。
并且保证必须是-1.22173 弧度∠b0 弧度∠c 此标准格式,否则此计算公式不适用。
1.309 弧度∠d0 弧度∠e 1.16937 弧度∠f0 弧度h1给定54.69 mmh2给定140.8 mmh3给定39.09 mm BC段长度L BC h1(1+tg2a+tg2d)0.5159.90 mm CD段长度L CD h2(1+tg2b+tg2e)0.5360.35 mm DE段长度L DE h3(1+tg2c+tg2f)0.5151.03 mm计算题3符合标准格式一,二面角计算名称符号计算结果单位投影角β1注:角度符号为标准格式(见上0.2618 弧度β'1图)。