基于Matlab 的对过程控制系统的PID 整定
- 格式:doc
- 大小:39.00 KB
- 文档页数:4



基于MA TL AB 的PID 参数整定周 晖(船舶重工集团公司723研究所,扬州225001)摘要:比例积分微分(PID )控制器参数往往因整定不良、性能欠佳,对运行工况的适应性很差。
根据稳定边界法则,以某一控制模型为例介绍如何在MA TL AB 工具帮助下整定并验证PID 控制器参数。
关键词:比例积分微分;稳定边界法;控制器中图分类号:TN273 文献标识码:A 文章编号:CN3221413(2008)022*******PID Parameter R eduction B ased on MAT LABZHOU Hui(The 723Institute of CSIC ,Yangzhou 225001,China )Abstract :The parameter adaptability of p roportion 2integral 2differential (PID )cont roller to t he op 2erating sit uation is very bad sometimes because t he reduction and performance isn ’t good.According to t he stable boundary principle ,t his paper int roduces how to reduce and validate t he PID cont rol 2ler parameter wit h t he help of MA TL AB tool taking a certain cont rol model as an example.K ey w ords :proportion 2integral 2differential ;stable bo undary principle ;cont roller0 引 言PID 控制是最早发展起来的控制策略之一,因为它所涉及的设计算法和控制结构都很简单,因此,被广泛应用于过程控制和运动控制中。

控制系统PID参数整定方法的MATLAB仿真1. 引言PID控制器是一种常见的控制算法,广泛应用于自动控制系统中。
其通过调节三个参数:比例增益(Proportional gain)、积分时间常数(Integral time constant)和微分时间常数(Derivative time constant),实现对被控对象的稳态误差、响应速度和稳定性等性能指标的调节。
PID参数的合理选择对控制系统的性能至关重要。
本文将介绍PID控制器的经典整定方法,并通过MATLAB软件进行仿真,验证整定方法的有效性。
2. PID控制器的整定方法2.1 手动整定法手动整定法是根据经验和试错法来选择PID参数的方法。
具体步骤如下:1.将积分时间常数和微分时间常数设为零,仅保留比例增益,将比例增益逐渐增大直至系统产生较大的超调现象。
2.根据超调响应的情况,调整比例增益,以使系统的超调量接近所需的范围。
3.逐步增加微分时间常数,观察系统的响应速度和稳定性。
4.增加积分时间常数,以减小系统的稳态误差。
手动整定法的优点是简单易行,但需要经验和反复试验,对控制系统要求较高。
2.2 Ziegler-Nichols整定法Ziegler-Nichols整定法是一种基于试探和试错法的自整定方法,该方法通过调整系统的输入信号,观察系统的输出响应,从而确定PID参数。
具体步骤如下:1.将I和D参数设为零,仅保留P参数。
2.逐步增大P参数,直到系统的输出出现大幅度的振荡。
3.记录下此时的P参数值,记为Ku。
4.根据振荡的周期Tp,计算出系统的临界增益Kc = 0.6 * Ku。
5.根据系统的类型选择相应的整定法则:–P型系统:Kp = 0.5 * Kc,Ti = ∞,Td = 0–PI型系统:Kp = 0.45 * Kc,Ti = Tp / 1.2,Td = 0–PID型系统:Kp = 0.6 * Kc,Ti = Tp / 2,Td = Tp / 82.3 Cohen-Coon整定法Cohen-Coon整定法是基于频域曲线拟合的方法,主要应用于一阶和二阶系统的整定。

matlab自整定pid算法
MATLAB中有多种方法可以自整定PID算法,以下是其中两
种常见的方法:
1. Ziegler-Nichols方法:
- 首先,将PID控制器的P和I增益设置为零,将D增益设置
为一个较小的非零值。
- 增加P增益,直到系统出现持续的高频振荡。
记录下此时的
P增益,记为Ku。
- 根据振荡的周期T,计算出临界增益Kc:Kc = 0.6 * Ku。
- 将PID控制器的增益重新设置为零,根据以下公式计算PID
控制器的增益:Kp = 0.6 * Kc,Ki = 1.2 / (T * Kc),Kd = 0.075 / (T * Kc)。
- 将这些增益值设置到PID控制器中,进行实际的控制。
2. AMIGO方法:
- 首先,收集系统的开环响应数据,包括输入信号和输出信号。
- 使用AMIGO工具箱读取数据并进行预处理。
- 选择合适的模型结构,例如一阶传递函数、二阶传递函数等。
- 使用AMIGO工具箱中的模型校准方法,例如最小二乘法或
极大似然法,将模型参数校准到实际数据中。
- 根据得到的模型参数,计算PID控制器的增益值。
- 将这些增益值设置到PID控制器中,进行实际的控制。
根据具体的系统和要求,可以选择适合的自整定方法,并使用MATLAB进行实现。
Matlab自整定PID算法一、介绍PID算法PID控制算法是一种经典的反馈控制算法,PID分别代表比例(proportional)、积分(integral)和微分(derivative)。
它是一种线性控制算法,最早应用于工业控制领域,后来被广泛应用于自动化、机器人、航空航天等领域。
PID算法的基本原理是通过对系统的误差进行比例、积分和微分处理,来调节系统的控制量,使系统的输出值逐步趋近目标值。
二、Matlab中的PID控制Matlab作为一种功能强大的科学计算软件,提供了丰富的控制算法工具箱。
在Matlab中,可以通过内置的PID控制器对象来实现PID算法。
可以使用MATLAB提供的PID类对象,也可以自行实现PID算法的代码。
三、Matlab自整定PID算法对于控制系统中的PID参数(Kp、Ki、Kd),通常需要通过试错法来调节,这样既费时又费力。
Matlab提供了自整定PID控制器工具箱,可以根据系统的性能指标自动生成PID参数。
与传统的手动调节相比,自整定PID算法具有以下优势:1. 时间效率:自整定PID算法可以快速生成合适的PID参数,节省了调试时间,提高了工作效率。
2. 精度:自整定PID算法可以根据系统的性能指标精确地生成最优的PID参数,使系统的控制性能得到优化。
3. 应用广泛:自整定PID算法适用于不同类型的系统,包括传统的工业控制系统、机器人系统、航空航天系统等。
四、Matlab自整定PID算法的原理Matlab自整定PID算法的原理主要是基于系统的数学模型和系统的性能指标。
在实际应用中,通常需要对系统进行数学建模,提取系统的参数,并根据系统的性能要求来自动生成PID参数。
MATLAB的自整定PID算法主要包括以下步骤:1. 系统建模:将控制系统的数学模型转化为MATLAB的控制系统模型,提取系统的参数,如传递函数、状态空间模型等。
2. 设定性能指标:根据控制系统的性能要求,设定性能指标,如超调量、调节时间、稳定性等。
基于MATLAB的PID 控制器设计基于MATLAB的PID 控制器设计一、PID控制简介PID控制是最早发展起来的经典控制策略, 是用于过程控制最有效的策略之一。
由于其原理简单、技术成,在实际应用中较易于整定, 在工业控制中得到了广泛的应用。
它最大的优点是不需了解被控对象精确的数学模型,只需在线根据系统误差及误差的变化率等简单参数, 经过经验进行调节器参数在线整定, 即可取得满意的结果, 具有很大的适应性和灵活性。
积分作用:可以减少稳态误差, 但另一方面也容易导致积分饱和, 使系统的超调量增大。
微分作用:可提高系统的响应速度, 但其对高频干扰特别敏感, 甚至会导致系统失稳。
所以, 正确计算控制器的参数, 有效合理地实现PID控制器的设计,对于PID 控制器在过程控制中的广泛应用具有重要的理论和现实意义。
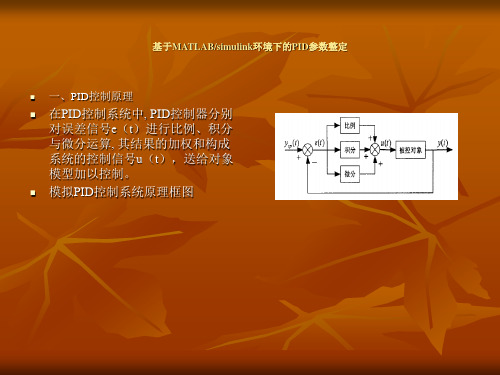
在PID控制系统中, PID控制器分别对误差信号e(t)进行比例、积分与微分运算, 其结果的加权和构成系统的控制信号u(t),送给对象模型加以控制。
PID控制器的数学描述为其传递函数可表示为:从根本上讲, 设计PID控制器也就是确定其比例系数Kp、积分系数T i 和微分系数T d , 这三个系数取值的不同, 决定了比例、积分和微分作用的强弱。
控制系统的整定就是在控制系统的结构已经确定、控制仪表和控制对象等处在正常状态的情况下, 适当选择控制器参数使控制仪表的特性和控制对象的特性相配合, 从而使控制系统的运行达到最佳状态, 取得最好的控制效果。
二、MATLAB的Ziegler-Nichols算法PID控制器设计。
1、PID控制器的Ziegler-Nichols参数整定在实际的过程控制系统中, 有大量的对象模型可以近似地由一阶模型来表示。
这个对象模型可以表示为sL-esT1KG(s)+=如果不能建立起系统的物理模型, 可通过试验测取对象模型的阶跃响应, 从而得到模型参数。
当然, 我们也可在已知对象模型的情况下, 利用MATLAB,通过使用step ( ) 函数得到对象模型的开环阶跃响应曲线。
基于Matlab 的对过程控制系统的PID 整定-企业管理论
文
基于Matlab 的对过程控制系统的PID 整定
孔凡杨
河南省心连心化肥有限公司河南新乡453700
摘要:本文就分析了串级控制系统的特点和设计,并分析了基于MATLAB 的增量式PID 算法应用在其中的应用,通过分析发现PID参数整定方法能够很好地实现串级控制系统的精度和稳定性。
关键词:MATLAB;串级控制;PID 整定
笔者在此介绍了一种采用基于MATLAB 的增量式PID 控制的双容无自衡串级贮槽液料控制系统,并在PID 参数整定方法的作用下实现了控制系统的良好控制效果。
1 串级控制系统的相关特点和设计分析
在对纯滞后和时间常数较大的对象控制中可使用串级控制系统,其对于系统控制质量的提高主要表现在以下几个方面,第一,是它能够很好地克服副回路中的二次干扰;第二,它能够使控制对象的时间常数减小;第三,它能够使动态特性在被控过程中得到改善,依此使控制系统的工作频率得以提高;第四,这种串级控制系统还能很好地适应操作条件和负荷的变化。
主回路和主参数的设计选择。
在某些条件下,最直接有效的质量指标也可被选为主参数,不然在选择主参数时相关人员还可以选择一个与产品质量有单值函数关系的参数,但是灵敏度和工艺过程的合理性是这个被选主参数必须满足的条件。
副回路和副参数的设计与选定。
较强的抑制扰动能力和较快的调节速度是串级控制系统副回路具备的主要优势,所以相关人员可以把尽可能多的一些扰动干扰放在副回路的设计中以充分利用副回路自身的优势,使其减少干扰对主参数的影响以提高其控制质量。
2 基于MATLAB 的串级控制系统分析
本文介绍的是一个串联式双容无自衡液位过程,由上方的进料管液料流进贮槽S1,然后再经过管道液料又流进贮槽S2,这时液料的流出受到变频调速器的控制,如果此变频调速器的工作频率是固定不变的,那么一个积分时间常数不变的积分环节就会在贮槽S2 中构成,在当前的工艺生产过程中液料位通常被要求在贮槽S2 中保持某一定值,令被控制量为h,使S1 中进料体积流量q 为控制变量,在这种情况下这个串联式双容无自衡液位过程的机构式可列为:
在这个串级控制系统中(如上图所示),副参数被选择为贮槽S1,主参数被选择为贮槽S2 的液位h,当控制系统运行时来自反馈的贮槽液位测量值就会被变频器收集并实现与设定值的对此,之后相关数据值就会被送入PID 模块进行计算,并实现输出频率的自动更改,以对液料流量和电机的转速实现调整,从而使贮槽液位实现稳定,和贮槽S1、S2 分别对应的液位传感器1 和2 将对其对应的贮槽信号的检测结果在A /D 转换的作用下传送到计算机,然后分别与两个PID 调节器设定值对比,并实现对其差别进行判断和计算。
MATLAB 的两个PID 算法程序被上位机所调用,PID1 的输入信号就是
贮槽S2 液料位信号与事先的系统设定值对比得到的偏差;然后该偏差会在PID1 中实现运算并将信号输出,然后就将其作为槽S1 的系统设定值,然后将贮槽S1 液料位信号与该设定值进行对比,再将此偏差输入PID2 进行运算,然后利用D/A 转换应用于运算结果,从而使电机的输出频率被改变,实现了对水泵转速的调整,从而使控制系统实现了对贮槽S1 控制,进而也控制了S2 的目的。
3 串级系统的PID 参数整定
在串级系统的整定中试凑法、两步和一步整定法是主要运用的工程整定方法。
具体如下,首先应选一适当的副调节器,对其设置要根据纯比例控制规律并放大倍数KC2,在主调节器的设置中也应先置于纯比例控制规律作用下,然后将实现整个控制系统的工作,并在这个过程中利用相关单回路整定方法使主调节器参数实现调整,并在施行干扰的情况下,观察相关的运行状况,并在KC1 和KC2 相互匹配原理的支持下实现对调节器参数的改进,经过对系统的多次调试,当液位在贮槽S2 中实现快速稳定于设定值时,反馈值也与设定值相同,当液位稳定后将扰动干扰加于贮槽S1,如果在副回路的校正作用下液位还受到影响的话,为了克服这种扰动的干扰主回路应该对此进一步实施调节,而保证扰动影响的消除,使液位处在设定值上。
依据此系统的工程整定方法中一步整定法对系统的参数进行整定如下:副调节器的放大倍数KC2 设定为2,然使将积分系数Ki2被设定为1000,之后对主调节器的参数整定根据4颐1 衰减曲线法实施,可以得到啄S1 为12.5%,TS1 为7s,参数整定后的实时控制曲线如下:
综上所述,这种采用基于MATLAB 的增量式PID 控制的双容无自衡串级贮槽液料控制系统,在PID 参数整定方法的作用下实现了控制系统的良好控制效果。
参考文献:
[1]何东健,刘忠超,范灵燕.基于MATLAB 的PID 控制器参数整定及仿真[J].西安科技大学学报,2006,26(4):511-514.
[2]唐贤伦,仇国庆,李银国,等.基于MATLAB 的PID 算法在串级控制系统中的应用[J].重庆大学学报(自然科学版),2005,28(9):61-63.
[3]赵永娟,孙华东.基于Matlab 的模糊PID 控制器的设计和仿真[J].微计算机信息,2009(1):48-49.。