PID控制算法的MATLAB仿真

题目：以PID控制进行系统仿真学院自动化学院专业班级工业自动化111班学生姓名黄熙晴目录1 引言 (1)1.1本论文研究内容 (1)2 PID控制算法 (1)2.1模拟PID控制算法 (1)2.2数字式PID控制算法 (3)2.3PID控制算法的改进 (5)2.3.1微分项的改进 (5)2.3.2积分项的改进 (9)2.4模糊PID控制算法 (11)2.4.1模糊推理的系统结构 (12)2.4.2 PID参数在线整定原则 (12)2.5PID控制器研究面临的主要问题 .................................. 错误！未定义书签。

3 MATLAB编程和仿真 (13)3.1PID控制算法分析 (13)3.2MATLAB仿真 (15)4结语 (20)参考文献...................................................................................... 错误！未定义书签。

1 引言PID控制器以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制的主要技术之一。

光学表面等离子共振生物传感技术受温度影响很大，因此设计高精度的温度控制器对于生物分析仪十分重要。

研究PID的控制算法是PID控制器整定参数优化和设定的关键技术之一。

在工业过程控制中，目前采用最多的控制方式依然是PID方式。

它具有容易实现、控制效果好、鲁棒性强等特点，同时它原理简单，参数物理意义明确，理论分析体系完整，并为工程界所熟悉，因而在工业过程控制中得到了广泛应用。

在实际的应用中，许多被控过程机理复杂，具有高度非线性、时变不确定性和纯滞后等特点，特别是在噪声、负载扰动等因素的影响下，参数复杂烦琐的整定过程一直困扰着工程技术人员。

为了减少参数整定的工作量，克服因环境变化或扰动作用造成系统性能的降低，就要提出一种PID控制参数的自动整定。

1.2本论文研究内容本文在介绍传统的PID控制算法，并对传统算法改进后，在学习的基础上提出一种模糊参数自整定方法，这种模糊控制的PID算法必须精确地确定对象模型。

控制系统PID参数整定方法的MATLAB仿真1. 引言PID控制器是一种常见的控制算法，广泛应用于自动控制系统中。

其通过调节三个参数：比例增益（Proportional gain）、积分时间常数（Integral time constant）和微分时间常数（Derivative time constant），实现对被控对象的稳态误差、响应速度和稳定性等性能指标的调节。

PID参数的合理选择对控制系统的性能至关重要。

本文将介绍PID控制器的经典整定方法，并通过MATLAB软件进行仿真，验证整定方法的有效性。

2. PID控制器的整定方法2.1 手动整定法手动整定法是根据经验和试错法来选择PID参数的方法。

具体步骤如下：1.将积分时间常数和微分时间常数设为零，仅保留比例增益，将比例增益逐渐增大直至系统产生较大的超调现象。

2.根据超调响应的情况，调整比例增益，以使系统的超调量接近所需的范围。

3.逐步增加微分时间常数，观察系统的响应速度和稳定性。

4.增加积分时间常数，以减小系统的稳态误差。

手动整定法的优点是简单易行，但需要经验和反复试验，对控制系统要求较高。

2.2 Ziegler-Nichols整定法Ziegler-Nichols整定法是一种基于试探和试错法的自整定方法，该方法通过调整系统的输入信号，观察系统的输出响应，从而确定PID参数。

具体步骤如下：1.将I和D参数设为零，仅保留P参数。

2.逐步增大P参数，直到系统的输出出现大幅度的振荡。

3.记录下此时的P参数值，记为Ku。

4.根据振荡的周期Tp，计算出系统的临界增益Kc = 0.6 * Ku。

5.根据系统的类型选择相应的整定法则：–P型系统：Kp = 0.5 * Kc，Ti = ∞，Td = 0–PI型系统：Kp = 0.45 * Kc，Ti = Tp / 1.2，Td = 0–PID型系统：Kp = 0.6 * Kc，Ti = Tp / 2，Td = Tp / 82.3 Cohen-Coon整定法Cohen-Coon整定法是基于频域曲线拟合的方法，主要应用于一阶和二阶系统的整定。

PID算法设计MATLAB课程设计一、课程目标知识目标：1. 掌握PID算法的基本原理，理解其参数调整对系统性能的影响；2. 学会使用MATLAB软件进行PID控制器的设计与仿真；3. 了解PID控制在实际工程中的应用及优化方法。

技能目标：1. 能够运用所学知识，独立设计简单的PID控制系统；2. 能够运用MATLAB软件进行PID控制器参数调整及系统性能分析；3. 能够通过课程学习，提高解决实际工程问题的能力。

情感态度价值观目标：1. 培养学生对自动控制技术的兴趣，激发其学习热情；2. 培养学生严谨的科学态度和团队协作精神；3. 增强学生对我国科技创新能力的信心，激发其为国家发展贡献力量的决心。

课程性质：本课程为实践性较强的课程，结合理论知识与实际操作，培养学生的动手能力和解决实际问题的能力。

学生特点：学生具备一定的自动控制理论基础，对MATLAB软件有一定了解，但对PID算法及其实际应用尚不熟悉。

教学要求：结合学生特点和课程性质，注重理论与实践相结合，以案例教学为主，充分调动学生的主观能动性，提高学生的实际操作能力。

在教学过程中，关注学生的个体差异，给予个性化指导，确保学生能够达到预设的课程目标。

通过课程学习，使学生能够具备独立设计PID控制系统并进行性能分析的能力。

二、教学内容1. PID算法基本原理：介绍PID控制器的定义、工作原理及其在自动控制中的应用；分析比例、积分、微分三个环节对系统性能的影响。

教材章节：第五章第二节2. MATLAB软件操作：回顾MATLAB软件的基本操作，重点掌握Simulink 环境下搭建仿真模型的方法。

教材章节：第四章3. PID控制器设计：讲解如何使用MATLAB/Simulink进行PID控制器的设计与参数调整；分析不同参数设置对系统性能的影响。

教材章节：第五章第三节4. PID控制系统仿真：通过实际案例，演示如何运用MATLAB进行PID控制系统的仿真，分析系统性能指标。

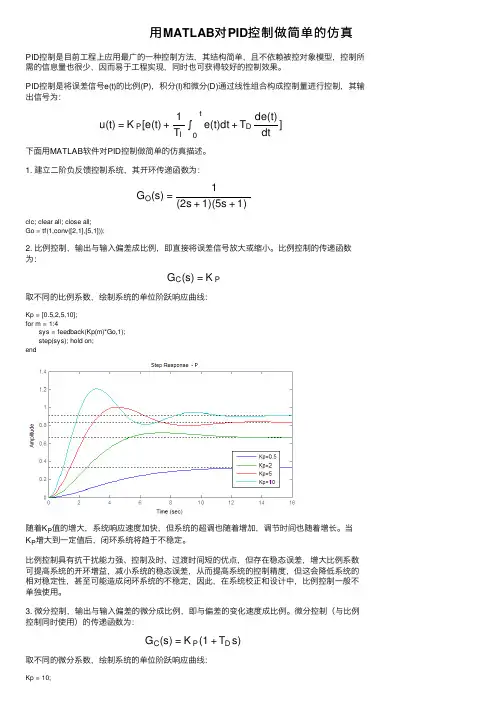
⽤MATLAB 对PID 控制做简单的仿真PID 控制是⽬前⼯程上应⽤最⼴的⼀种控制⽅法，其结构简单，且不依赖被控对象模型，控制所需的信息量也很少，因⽽易于⼯程实现，同时也可获得较好的控制效果。

PID 控制是将误差信号e(t)的⽐例(P)，积分(I)和微分(D)通过线性组合构成控制量进⾏控制，其输出信号为：下⾯⽤MATLAB 软件对PID 控制做简单的仿真描述。

1. 建⽴⼆阶负反馈控制系统，其开环传递函数为：clc; clear all; close all;Go = tf(1,conv([2,1],[5,1]));2. ⽐例控制，输出与输⼊偏差成⽐例，即直接将误差信号放⼤或缩⼩。

⽐例控制的传递函数为：取不同的⽐例系数，绘制系统的单位阶跃响应曲线：Kp = [0.5,2,5,10];for m = 1:4 sys = feedback(Kp(m)*Go,1); step(sys); hold on;end随着K P 值的增⼤，系统响应速度加快，但系统的超调也随着增加，调节时间也随着增长。

当K P 增⼤到⼀定值后，闭环系统将趋于不稳定。

⽐例控制具有抗⼲扰能⼒强、控制及时、过渡时间短的优点，但存在稳态误差，增⼤⽐例系数可提⾼系统的开环增益，减⼩系统的稳态误差，从⽽提⾼系统的控制精度，但这会降低系统的相对稳定性，甚⾄可能造成闭环系统的不稳定，因此，在系统校正和设计中，⽐例控制⼀般不单独使⽤。

3. 微分控制，输出与输⼊偏差的微分成⽐例，即与偏差的变化速度成⽐例。

微分控制（与⽐例控制同时使⽤）的传递函数为：取不同的微分系数，绘制系统的单位阶跃响应曲线：Kp = 10;u(t)=[e(t)+e(t)dt +]K P 1T I ∫t 0T D de(t)dt(s)=G O 1(2s +1)(5s +1)(s)=G C K P(s)=(1+s)G C K P T DTd = [0,0.4,1,4];for m = 1:4 G1 = tf([Kp*Td(m),Kp],[0,1]); sys = feedback(G1*Go,1); step(sys); hold on;end随着T D 值的增⼤，系统超调量逐渐减⼩，动态特征有改善。

下面用一个简单的例子作介绍：（本例不是特别针对实现什么功能，只是为了介绍方便）第一部分创建一个模糊逻辑（.fis文件）第一步：打开模糊推理系统编辑器步骤：在Commond Window 键入fuzzy回车打开如下窗口，既模糊推理系统编辑器第二步：使用模糊推理系统编辑器本例用到两个输入，两个输出，但默认是一个输人，一个输出步骤：1、添加一个输入添加一个输出得如下图2、选择Input、output(选中为红框)，在Name框里修改各输入的名称并将And method 改为prod，将Or method 改为probor提示：在命名时’_’在显示时为下标，可从上图看出。

第三步：使用隶属函数编辑器该编辑器提供一个友好的人机图形交互环境，用来设计和修改模糊推理系中各语言变量对应的隶属度函数的相关参数，如隶属度函数的形状、范围、论域大小等，系统提供的隶属度函数有三角、梯形、高斯形、钟形等，也可用户自行定义。

步骤：1、双击任何一个输入量（In_x、In_y）或输出量打开隶属度函数编辑器。

2、在左下处Range和Display Range处添加取值范围，本例中In_x和In_y的取值范围均为[0 10], Out_x和Out_y的取值范围均为[0 1]3、默认每个输入输出参数中都只有3个隶属度函数，本例中每个输入输出参数都需要用到五个，其余几个需要自己添加：选中其中一个输入输出参数点击Edit菜单，选Add MFS…打开下列对话框将MF type设置为trimf(三角形隶属度函数曲线，当然你也需要选择其他类型) 将Number of MFs设置为2点击OK按钮同样给其他三个加入隶属度函数4、选中任何一个隶属度函数（选中为红色），在Name中键入名称，在Type 中选择形状，在Params中键入范围，然后回车如下图：5、关闭隶属函数编辑器第四步：使用规则编辑器通过隶规则编辑器来设计和修改“IF...THEN”形式的模糊控制规则。

基于MATLAB的智能PID控制器设计与仿真摘要在工业生产中应用非常广泛的是PID控制器，是最早在经典控制理论基础上发展起来的控制方法，应用也十分广泛。

传统的PID控制器原理十分简单，即按比例、积分、微分分别控制的控制器，但是他的核心也是他的难点就是三个参数（比例系数Kp、积分系数Ki、微分系数Kd）的整定。

参数整定的合适，那么该控制器将凭借结构简单、鲁棒性好的优点出色的完成控制任务，反之则达不到人们所期望的控制效果。

人工神经网络模拟人脑的结构和功能而形成的信息处理系统，是一门十分前沿高度综合的交叉学科，并广泛应用于工程领域。

神经网络控制是把自动控制理论同他模仿人脑工作机制的数学模型结合起来，并拥有自学习能力，能够从输入—输出数据中总结规律，智能的处理数据。

该技术目前被广泛应用于处理时变、非线性复杂的系统，并卓有成效。

关键词自适应PID控制算法，PID控制器，神经网络Design and simulation of Intelligent PID Controllerbased on MATLABAbstractPID controller ,the control method which is developed on the basis of classical control theory, is widely used in industrial production.The Principle of traditional PID controller is very simple, which contains of the proportion, integral, differential three component, but its core task and difficulties is three parameter tuning(proportional coefficient Kp, integral coefficient Ki and differential coefficient KD).If the parameter setting is suitable, the controller can accomplish the control task with the advantages of simple structure and good robustness;but on the contrary, it can not reach the desired control effect which we what.Artificial neural network , the formation of the information processing system which simulate the structure and function of the human brain , is a very high degree of integration of the intersection of disciplines, and widely used in the field of engineering. Neural network control ,combining automatic control theory and the imitate mathematical model of the working mechanism of human brain , has self-learning ability, and can summarize the law of the input-output data , dealing with data intelligently .This technique has been widely used in the process of time-varying, nonlinear and complex system, and it is very effective.Key W ord:Adaptive PID control algorithm，PID controller，Neural network目录摘要 (I)Abstract (II)第一章绪论 (1)1.1 课题研究背景及意义 (1)第二章 PID控制器 (2)2.1 PID控制原理 (2)2.2常规PID控制器的算法理论 (3)2.2.1 模拟PI D控制器 (3)2.2.2 数字P I D控制算法 (3)2.2.3常规PID控制的局限 (5)2.2.4 改进型PID控制器 (5)第三章人工神经网络 (8)3.1 人工神经网络的原理 (8)3.2神经网络PID控制器 (8)3.2.1神经元PID控制器 (8)3.2.2 单神经元自适PID应控制器 (9)3.3 BP神经网络参数自学习的PID控制器 (12)第四章MATAB仿真 (16)4.1 仿真过程 (16)第五章结论与展望 (24)致谢 (25)参考文献 (25)华东交通大学毕业设计（论文）第一章绪论1.1 课题研究背景及意义在工业生产中应用非常广泛的是PID控制器，是最早在经典控制理论基础上发展起来的控制方法，应用也十分广泛。

基于MATLAB的PID控制器参数整定及仿真PID控制器是一种经典的控制器，在工业自动化控制系统中广泛应用。

其主要功能是根据系统的误差信号，通过调整输出信号的比例、积分和微分部分来减小误差，并达到系统的稳定控制。

PID控制器参数整定是指确定合适的比例常数Kp、积分常数Ki和微分常数Kd的过程。

本文将介绍基于MATLAB的PID控制器参数整定及仿真的方法。

首先，在MATLAB中建立一个包含PID控制器的模型。

可以通过使用MATLAB的控制系统工具箱来实现这一过程。

在工具箱中，可以选择合适的建模方法，如直接设计模型、积分节点模型或传输函数模型。

通过这些工具，可以方便地建立控制系统的数学模型。

其次，进行PID控制器参数整定。

PID控制器参数整定的目标是通过调整比例常数Kp、积分常数Ki和微分常数Kd，使系统的响应特性达到最佳状态。

常用的PID参数整定方法有经验法、试误法、Ziegler-Nichols方法等。

1.经验法：根据系统的特性和经验，选择合适的PID参数。

这种方法常用于初步整定，但可能需要根据实际情况调整参数。

2.试误法：通过逐步试验和调整PID参数，使系统的输出响应逐渐接近期望值，从而达到最佳控制效果。

3. Ziegler-Nichols方法：该方法是一种经典的系统辨识方法，通过测试系统的临界稳定性，得到系统的传递函数参数，并据此计算出合适的PID参数。

最后，进行PID控制器参数整定的仿真。

在MATLAB中，可以通过使用PID模块进行仿真。

可以输入相应的输入信号和初始参数，观察系统的输出响应，并通过调整参数，得到最佳的控制效果。

总结起来，基于MATLAB的PID控制器参数整定及仿真的过程包括：建立控制系统模型、选择PID参数整定方法、进行PID参数整定、进行仿真实验。

PID控制器参数整定的好坏直接影响控制系统的工作性能。

通过基于MATLAB的仿真实验，可以方便地调整和优化控制系统的PID参数，提高系统的响应速度、稳定性和抗干扰性能。

PID的MATLAB仿真程序：%PID Controler 不完全微分clear all;close all;ts=20;sys=tf([1],[60,1],'inputdelay',80);dsys=c2d(sys,ts,'zoh');[num,den]=tfdata(dsys,'v');u_1=0;u_2=0;u_3=0;u_4=0;u_5=0;ud_1=0;y_1=0;y_2=0;y_3=0;error_1=0;ei=0;for k=1:1:100time(k)=k*ts;rin(k)=1.0;%Linear modelyout(k)=-den(2)*y_1+num(2)*u_5;D(k)=0.01*rands(1);yout(k)=yout(k)+D(k);error(k)=rin(k)-yout(k);%PID Controller with partly differential ei=ei+error(k)*ts;kc=0.30;ki=0.0055;TD=140;kd=kc*TD/ts; Tf=180;Q=tf([1],[Tf,1]); %Low Freq Signal FilterM=2; %M=1不完全微分，%M=2普通Pid控制！！if M==1%Using PID with Partial differentialalfa=Tf/(ts+Tf);ud(k)=kd*(1-alfa)*(error(k)-error_1)+alf a*ud_1;u(k)=kc*error(k)+ud(k)+ki*ei;ud_1=ud(k);elseif M==2 %Using Simple PIDu(k)=kc*error(k)+kd*(error(k)-error_1)+ ki*ei;end%Restricting the output of controllerif u(k)>=10u(k)=10;endif u(k)<=-10u(k)=-10;endu_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=u(k);y_3=y_2;y_2=y_1;y_1=yout(k);error_1=error(k);endfigure(1);plot(time,rin,'b',time,yout,'r');xlabel('time(s)');ylabel('rin,yout');由仿真结果可以看出，采用不完全微分型PID算法，引入不完全微分后能有效克服普通PID的不足，尽管不完全微分算法比普通PID控制算法要复杂的多，但由于其良好的控制特性，近年来越来越广泛的应用。

模糊PID控制及其MATLAB实现姓名：专业班级：学号：授课教师：摘要PID（比例积分微分）控制具有结构简单、稳定性能好、可靠性高等优点,尤其适用于可建立精确数学模型的控制系统。

而对于一些多变量、非线性、时滞的系统，传统的PID控制器并不能达到预期的效果。

随着模糊数学的发展，模糊控制的思想逐渐得到控制工程师们的重视，各种模糊控制器也应运而生。

而单纯的模糊控制器有其自身的缺陷—控制效果很粗糙、控制精度无法达到预期标准。

但利用传统的PID控制器和模糊控制器结合形成的模糊自适应的PID控制器可以弥补其缺陷；它将系统对应的误差和误差变化率反馈给模糊控制器进而确定相关参数，保证系统工作在最佳状态，实现优良的控制效果。

论文介绍了参数自适应模糊PID控制器的设计方法和步骤。

并利用MATLAB 中的SIMULINK 和模糊逻辑推理系统工具箱进行了控制系统的仿真研究，并简要地分析了对应的仿真数据。

关键词: 经典PID控制; 模糊控制; 自适应模糊PID控制器; 参数整定; MATLAB仿真ABSTRACTPID(Proportion Integration Differentiation) control, with lots of advantages including simple structure, good stability and high reliability, is quite suitable to establish especially the control system which accurate mathematical model is available and needed. However, taken multivariable, nonlinear and time-lag into consideration, traditional PID controller can not reach the expected effect.Along with the development of Fuzzy Mathematics, control engineers gradually pay much attention to the idea of Fuzzy Control, thus promoting the invention of fuzzy controllers. However, simple fuzzy controller has its own defect, where control effect is quite coarse and the control precision can not reach the expected level. Therefore, the Fuzzy Adaptive PID Controller is created by taking advantage of the superiority of PID Controller and Fuzzy Controller. Taken this controller in use, the corresponding error and its differential error of the control system can be feed backed to the Fuzzy Logic Controller. Moreover, the three parameters of PID Controller is determined online through fuzzification, fuzzy reasoning and defuzzification of the fuzzy system to maintain better working condition than the traditional PID controller.Meanwhile，the design method and general steps are introduced of the Parameter self-setting Fuzzy PID Controller. Eventually, the Fuzzy Inference Systems Toolbox and SIMULINK toolbox are used to simulate Control System. The results of the simulation show that Self-organizing Fuzzy Control System can get a better effect than the Classical PID controlled evidently.Keywords: Classic PID control; Fuzzy Control; Parameters tuning; the Fuzzy Adaptive PID Controller; MATLAB simulation目录第一章绪论 (1)1.1 研究的背景及意义 (1)1.2 经典PID控制系统的分类与简介 (2)1.2.1 P控制 (2)1.2.2 PI控制 (2)1.2.3 PD控制 (2)1.2.4 比例积分微分（PID）控制 (2)1.3 模糊逻辑与模糊控制的概念 (3)1.3.1 模糊控制相关概念 (3)1.3.2 模糊控制的优点 (4)1.4 模糊控制技术的应用概况 (4)1.5 本文的研究目的和内容 (5)第二章PID控制 (6)2.1 PID的算法和参数 (6)2.1.1 位移式PID算法 (6)2.1.2 增量式PID算法 (7)2.1.3 积分分离PID算法 (7)2.1.4 不完全微分PID算法 (8)2.2 PID参数对系统控制性能的影响 (9)2.2.1 比例系数K P对系统性能的影响 (9)2.2.2 积分时间常数T i对系统性能的影响 (9)2.2.3 微分时间常数T d对系统性能的影响 (9)2.3 PID控制器的选择与PID参数整定 (10)2.3.1 PID控制器的选择 (10)2.3.2 PID控制器的参数整定 (10)第三章模糊控制器及其设计 (11)3.1 模糊控制器的基本结构与工作原理 (11)3.2 模糊控制器各部分组成 (11)3.2.1 模糊化接口 (11)3.2.2 知识库 (12)3.2.3 模糊推理机 (12)3.2.4 解模糊接口 (13)3.3模糊推理方式 (13)3.3.1 Mamdani模糊模型（迈达尼型） (13)3.3.2 Takagi-Sugeno模糊模型(高木-关野) (13)3.4模糊控制器的维数确定 (14)3.5 模糊控制器的隶属函数 (15)3.6模糊控制器的解模糊过程 (17)3.7 模糊PID控制器的工作原理 (18)第四章模糊PID控制器的设计 (19)4.1 模糊PID控制器组织结构和算法的确定 (19)4.2 模糊PID控制器模糊部分设计 (19)4.2.1 定义输入、输出模糊集并确定个数类别 (19)4.2.2 确定输入输出变量的实际论域 (20)4.2.3 定义输入、输出的隶属函数 (20)4.2.4 确定相关模糊规则并建立模糊控制规则表 (20)第五章模糊PID控制器的MATLAB仿真 (24)5.1 模糊PID控制的仿真 (24)5.1.1 FIS编辑器 (24)5.1.2 隶属函数 (25)5.1.3 模糊规则库 (25)5.2 对模糊控制器编程仿真 (27)第六章结语 (31)参考文献 (32)第一章绪论1.1 研究的背景及意义随着越来越多的新型自动控制应用于实践，其控制理论的发展也经历了经典控制理论、现代控制理论和智能控制理论三个阶段。

基于matlab的pid控制仿真课程设计PID（比例-积分-微分）控制器是一种常见的控制算法，被广泛应用于工业控制系统中。

在本文中，我们将介绍基于MATLAB的PID控制仿真课程设计。

首先，我们将简要介绍PID控制器的原理和特点，然后介绍如何使用MATLAB进行PID控制的仿真。

PID控制器是一种反馈控制器，可以通过比例、积分和微分三部分来调节控制系统的输出。

比例部分根据误差的大小进行调节，积分部分用于消除稳态误差，微分部分用于抑制系统振荡。

通过调节PID控制器的参数，可以使系统的稳定性、响应速度和稳态误差达到预期的要求。

在MATLAB中，可以使用控制系统工具箱来进行PID控制的仿真。

首先，我们需要定义一个系统模型，可以是连续时间系统或离散时间系统。

然后，我们可以使用PID控制器对象来创建一个PID控制器。

PID控制器的参数可以通过试错法、模型辨识等方法进行调节。

一旦系统模型和PID控制器被定义，我们可以使用MATLAB中的仿真工具来进行PID控制器的仿真。

通常，我们将输入信号作为控制器的参考信号，将输出信号作为系统的输出，并将控制器的输出作为系统的输入。

然后，我们可以观察系统的响应，并根据需要调整控制器的参数。

在进行PID控制仿真实验时，我们可以通过选择不同的控制器参数、改变控制器的结构、调整参考信号等方式来研究控制系统的性能。

例如，我们可以改变比例增益来改变系统的稳定性和响应速度，增加积分时间常数来减小稳态误差，增加微分时间常数来抑制系统振荡等。

在课程设计中，我们可以设计不同的控制实验，并分析不同参数对系统性能的影响。

例如，可以研究比例增益对系统稳定性和响应速度的影响，或者研究积分时间常数对稳态误差的影响等。

同时，我们还可以通过比较PID控制和其他控制算法（如PI控制、PD控制等）来评估PID控制的优势和局限性。

在进行PID控制仿真实验时，我们应该注意以下几点。

首先，选择合适的系统模型，确保模型能够准确地描述实际系统的行为。

控制系统pid参数整定方法的matlab仿真
控制系统PID参数整定方法的MATLAB仿真，可以分为以下几个步骤：
1. 建立模型。

在MATLAB中建立你要进行PID参数整定的模型，比如电机速度控制系统或温度控制系统。

2. 设计控制器。

根据建立的模型，设计出对应的PID控制器，并将其加入到系统中。

3. 确定初始参数。

在进行PID参数整定前，需要确定PID控制器的初始参数。

通常可以选择Ziegler-Nichols方法、Chien-Hrones-Reswick方法等经典的PID参数整定法则来确定初始参数。

4. 仿真模拟。

使用MATLAB中的仿真工具，对整定后的PID控制器进行仿真模拟，并记录下系统的响应曲线和各项性能指标。

5. 调整参数。

根据仿真结果，对PID控制器的参数进行适当的调整，以达到更理想的控制效果。

6. 再次仿真模拟。

调整完参数后，再次使用MATLAB中的仿真工具，对整定后的PID控制器进行仿真模拟，并比较其与上一次仿真的差异，以确认调整是否合理。

7. 实现控制。

最后，将优化后的PID控制器应用到实际控制系统中，进行控制。

总的来说，PID参数整定是一个相对复杂的过程，需要根据具体情况选择合适的方法和工具。

MATLAB作为一种强大的数学计算软件，可以提供丰富的工具和函数，方便进行控制系统的建模和仿
真，也可以帮助我们更好地进行PID参数整定。

PID控制算法的MATLAB仿真假设我们现在要设计一个PID控制器来控制一个被控对象，该对象的传递函数为G(s)。

首先，我们需要确定PID控制器的参数。

这些参数包括比例增益Kp、积分时间Ti和微分时间Td。

在Simulink中，我们可以使用以下步骤来进行PID控制的仿真：1. 打开MATLAB，并在工具栏上选择Simulink模块。

2. 在Simulink模块中，选择一个PID控制器模块，并将其拖放到工作区域中。

4.将被控对象的传递函数G(s)添加到工作区域中，并将其与PID控制器模块连接起来。

5.添加一个把期望值作为输入的信号源，并将其连接到PID控制器模块的输入端口上。

6.添加一个作为输出的信号源，并将其与被控对象的输出端口连接起来。

7. 在Simulink模块中运行仿真。

下面以一个简单的例子来说明PID控制的仿真过程。

假设我们要控制一个小车的速度，将其速度控制在一个期望值上。

小车的动力学方程可以表示为：m * V_dot = F - B * V其中，m为小车的质量，V为小车的速度，F为施加在小车上的力，B 为摩擦系数。

首先，我们需要将动力学方程转化为传递函数的形式。

假设小车的传递函数为：G(s)=1/(m*s+B)在Simulink中，可以通过使用Transfer Fcn模块来表示传递函数。

在工作区域中添加该模块，并设置其参数为1 / (m * s + B)。

接下来，我们需要添加PID控制器模块，并设置其参数。

假设我们选择Kp=1,Ti=0.5,Td=0.1作为PID控制器的参数。

将信号源（期望值）和输出信号（小车速度）连接到PID控制器模块。

然后，将PID控制器的输出连接到小车动力学方程的输入端口。

最后，点击Simulink模块中的“运行”按钮，即可开始仿真。

在进行仿真时，可以观察小车速度是否能够达到期望值，并调整PID控制器的参数以获得更好的控制效果。

通过以上步骤，在MATLAB中可以很方便地进行PID控制的仿真。