理论力学2016年南京航空航天大学硕士研究生考试真题
- 格式:pdf
- 大小:254.86 KB
- 文档页数:3
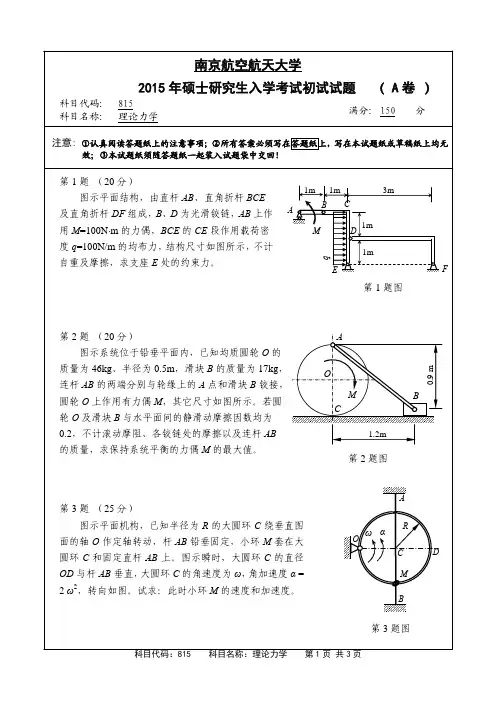

南京航空航天⼤学考研理论⼒学习题册12⼀、概念题1.在⼀组平⾏轴中,刚体对质⼼轴的转动惯量()。
①最⼤②最⼩2.图⽰A、O、C三轴皆垂直于矩形板的板⾯。
已知⾮均质矩形板的质量为m,对A轴的转动惯量为J,点O为板的形⼼,点C 为板的质⼼。
若长度AO = a,CO = e,AC = l,则板对形⼼轴O的转动惯量为()。
①J-ma2②J+ma2③J-m(l2-e2)④J-m(l2+e2)3.图⽰均质圆环形盘的质量为m,内、外直径分别为d和D。
则此盘对垂直于盘⾯的中⼼轴O的转动惯量为()。
①md2/8②mD2/8③m(D2-d2)/8④m(D2+d2)/84.细绳跨过滑轮(不计滑轮和绳的重量),如图所⽰,⼀端系⼀砝码,⼀猴沿绳的别⼀端从静⽌开始以等速v向上爬,猴和砝码等重。
则砝码的速度()。
①⼤⼩等于v,⽅向向下②⼤⼩等于v,⽅向向上③⼤⼩不等于v④砝码不动5.均质杆AB,质量为m,两端⽤张紧的绳⼦系住,绕轴O转动,如图所⽰。
则杆AB对O轴的动量矩为()。
① 5/6ml2ω② 13/12 ml2ω③ 4/3 ml2ω④1/12ml2ω6.均质圆环绕z轴转动,在环中的A点处放⼀⼩球,如图所⽰。
在微扰动下,⼩球离开A点运动。
不计摩擦,则此系统运动过程中()。
①ω不变,系统对z轴动量矩守恒②ω改变,系统对z轴动量矩守恒③ω不变,系统对z轴动量矩不守恒④ω改变,系统对z轴动量矩不守恒7.如图所⽰,⼀半径为R,质量为m的圆轮,在下列两种情况下沿平⾯作纯滚动:(1)轮上作⽤⼀顺时针的⼒偶矩为M的⼒偶;(2)轮⼼作⽤⼀⼤⼩等于M/R的⽔平向右的⼒F。
若不计滚动摩擦,则两种情况下()。
①轮⼼加速度相等,滑动摩擦⼒⼤⼩相等②轮⼼加速度不相等,滑动摩擦⼒⼤⼩相等③轮⼼加速度相等,滑动摩擦⼒⼤⼩不相等④轮⼼加速度不相等,滑动摩擦⼒⼤⼩不相等8.⼀均质杆OA与均质圆盘在圆盘中⼼A处铰接,在图⽰位置时,OA杆绕固定轴O转动的⾓速度为ω,圆盘相对于杆OA的⾓速度也为ω。

2016江苏南京航空航天大学普通物理考研真题一填空题(每题 3 分,共 75 分)1 已知质点的运动学方程为,当 t =2 s 时,加速度的大小为 a =______________。
2 以初速率 V0 、抛射角抛出一物体,则其抛物线轨道最高点处的曲率半径为______________。
(重力加速度 g 为已知常数。
)3 质量为m 的小球自高为 y0处沿水平方向以速率 v0抛出,与地面碰撞后跳起的最大高度为,水平速率为,则碰撞过程中地面对小球的竖直冲量的大小为______________ 。
(重力加速度 g 为已知常数。
)4 一质量为 1kg 的物体,置于水平地面上,物体与地面之间的静摩擦系数=0.20,滑动摩擦系数=0.16,现对物体施一水平拉力 F=t+0.96(SI),则 2 秒末物体的速度大小 v =______________。
(已知重力加速度 g=9)5 地球的质量为 m,太阳的质量为 M,地心与日心的距离为 R,引力常量为 G,则地球绕太阳作圆周运动的轨道角动量为 L=_______________。
6 半径为 r=1.5m 的飞轮,初角速度=10,角加速度,则在t___________时角位移为零。
7 质量分别为m 和2m 的两物体(都可视为质点),用一长为l 的轻质刚性细杆相连,系统绕通过杆且与杆垂直的竖直固定轴 O 转动,已知 O 轴离质量为2m 的质点的距离为,质量为m 的质点的线速度为v 且与杆垂直,则该系统对转轴的角动量(动量矩)大小为___________________。
8 图示的曲线分别表示了氢气和氦气在同一温度下分子速率的分布情况。
由图可知,氢气分子的最概然速率为_______________。
(已知氢气的摩尔质量是,氦气的摩尔质量是。
)9 3 mol 的理想气体开始时处在压强 p1 =6 atm、温度 T1 =500 K 的平衡态。
经过一个等温过程,压强变为 p2 =3 atm。

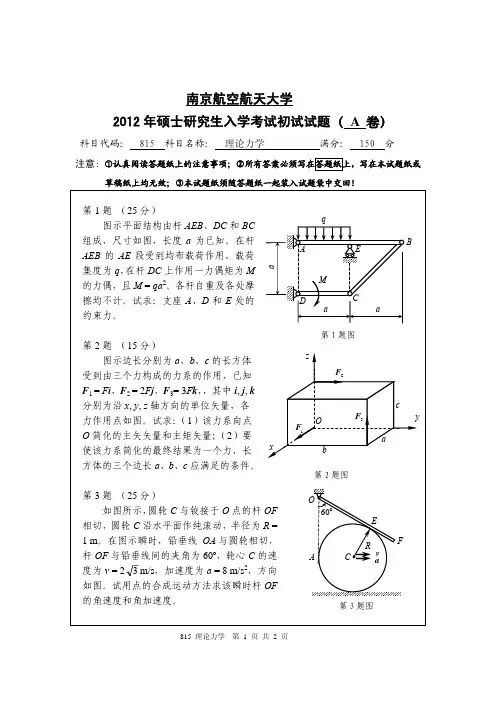

一、概念题1. 如图所示,半径为R ,质量为m 1的均质滑轮上,作用一常力矩M ,吊升一质量为m 2的重物。
当重物上升高度h 时,力矩M 所作的功为( )。
① Mh /R ② m 2gh③ Mh/R -m 2gh ④ 02.若质点的动能保持不变,则( )。
① 其动量必守恒 ② 质点必作直线运动③ 质点必作匀速直线运动 ④ 质点必作变速运动3.汽车靠发动机的内力做功,( )。
① 汽车肯定向前运动 ② 汽车肯定不能向前运动③ 汽车动能肯定不变 ④ 汽车动能肯定变化4.三棱柱B 沿三棱柱A 的斜面运动,三棱柱A 沿光滑水平面向左运动。
已知A 的质量为m 1,B 的质量为m 2;某瞬时A 的速度为v 1,B 沿斜面的速度为v 2。
则此时三棱柱B 的动能为 ( )。
① 22221v m ② 2212)(21v v m − ③ )(2122212v v m − ④ ]sin )cos [(212222212θθv v v m +−5.一质量为m ,半径为r 的均质圆轮以匀角速度ω沿水平面作纯滚动,均质杆OA 与圆轮在轮心O处铰接,如图所示。
设OA 杆长l = 4r ,质量M = m /4。
在图示杆与铅垂线的夹角φ = 60°时,其角速度ωOA = ω/2,则此时该系统的动能为( )。
① 222425ωmr T = ② 221211ωmr T = ③ 2267ωmr T = ④ 2232ωmr T =6.均质圆盘A ,半径为r ,质量为m ,在半径为R 的固定圆柱面内作纯滚动,如图所示。
则圆盘的动能为( )。
① 2243ϕ mr T = ② 2243ϕ mR T = ③ 22)(21ϕ r R m T −= ④ 22)(43ϕ r R m T −=7.图示均质圆盘沿水平直线轨道作纯滚动,在盘心移动了距离s 的过程中,水平常力F T 的功A T =( );轨道给圆轮的摩擦力F f 的功A f =( )。
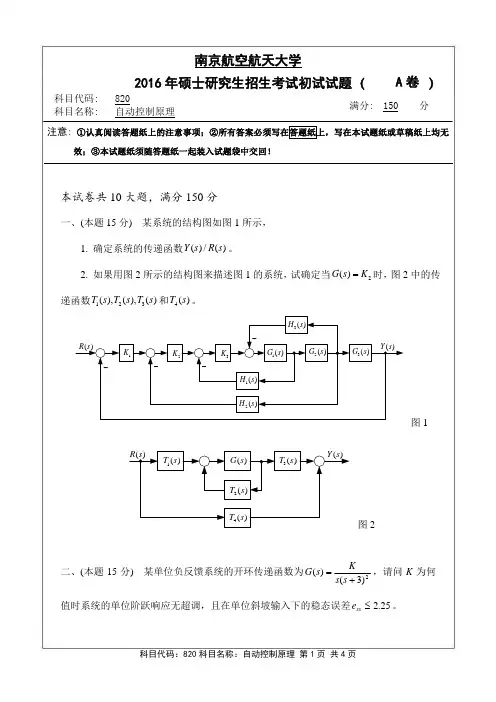

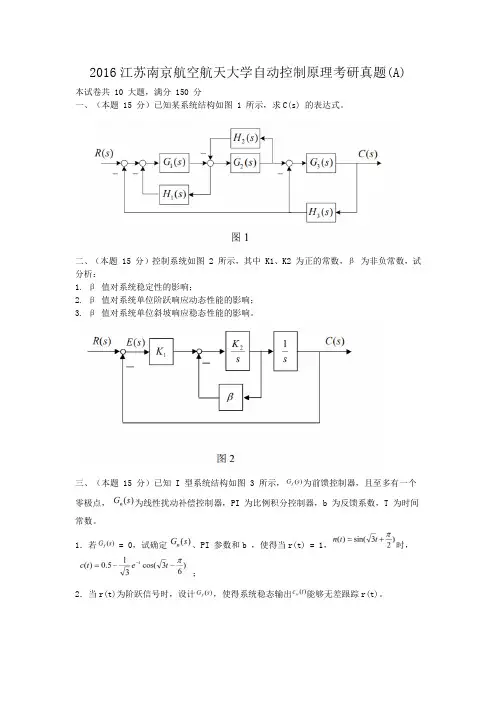
2016江苏南京航空航天大学自动控制原理考研真题(A)本试卷共 10 大题,满分 150 分一、(本题 15 分)已知某系统结构如图 1 所示,求C(s) 的表达式。
二、(本题 15 分)控制系统如图 2 所示,其中 K1、K2 为正的常数,β为非负常数,试分析:1. β值对系统稳定性的影响;2. β值对系统单位阶跃响应动态性能的影响;3. β值对系统单位斜坡响应稳态性能的影响。
三、(本题 15 分)已知 I 型系统结构如图 3 所示,为前馈控制器,且至多有一个零极点,为线性扰动补偿控制器,PI 为比例积分控制器,b 为反馈系数,T 为时间常数。
1.若 = 0,试确定、PI 参数和b ,使得当r(t) = 1,时,;2.当r(t)为阶跃信号时,设计,使得系统稳态输出能够无差跟踪r(t)。
四、(本题 15 分)系统结构如图 4 所示,其开环传递函数在s = −2之左具有一对重极点,试确定闭环系统处于临界阻尼时的a 、b 。
五、(本题 15 分)已知某单位反馈三阶系统,当输入信号r(t) = 2 + 0.5t 时,稳态误差为 0.5,系统开环幅相曲线如图 5 所示,试分析:1. 求系统临界稳定时的开环增益 Kc ;2. 若穿越频率ωx = 1,求系统的相角裕度γ,并绘制开环对数幅频渐近曲线;3. 试设计串联校正环节,使校正后系统满足截止频率ωc ≥ 1、相角裕度γ≥ 45°。
六、(本题 15 分)设系统结构图如图 6 所示,其中。
1. 试绘制a = 0 时的开环幅相曲线,并用奈氏判据判断该系统的闭环稳定性;2. a > 0 ,若系统开环截止频率ωc 为 4,问能否满足相角裕度γ >的要求;3. 讨论参数a 对系统稳定性的影响。
七、(本题 15 分)已知离散系统的结构图如图 7 所示,试分析:1. 判断系统稳定性,并分析采样周期T 对系统稳定性的影响;2. 若采样周期T = 0.4 ,输入信号为单位阶跃函数时,求c(3T) 。
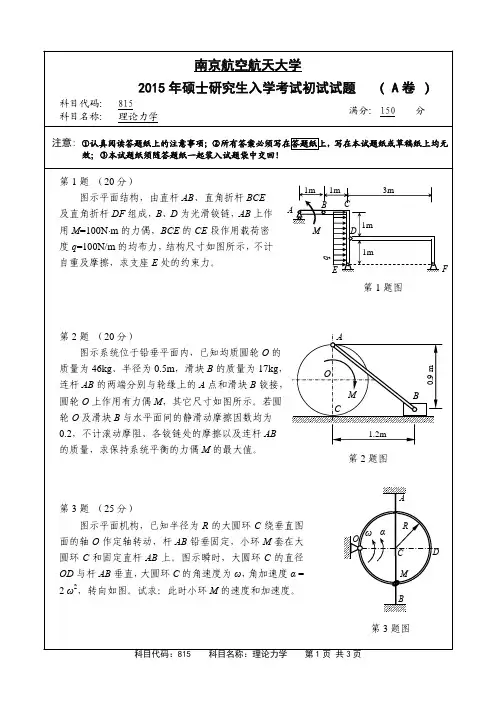
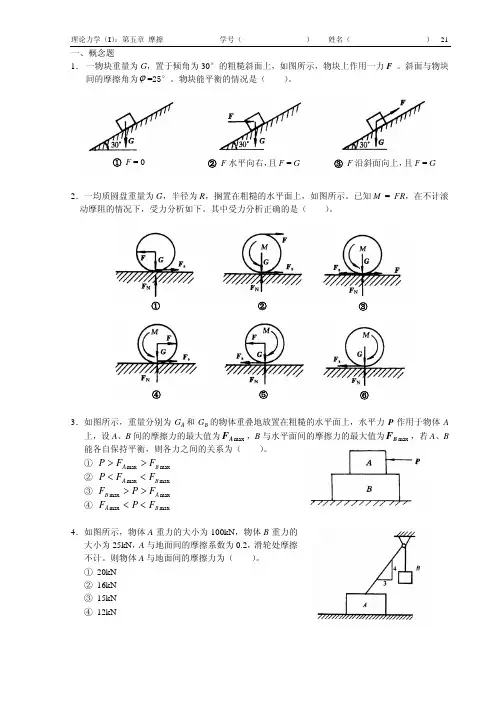
一、概念题1. 一物块重量为G ,置于倾角为30°的粗糙斜面上,如图所示,物块上作用一力F 。
斜面与物块间的摩擦角为ϕ=25°。
物块能平衡的情况是( )。
2.一均质圆盘重量为G ,半径为R ,搁置在粗糙的水平面上,如图所示。
已知M = FR ,在不计滚动摩阻的情况下,受力分析如下。
其中受力分析正确的是( )。
3.如图所示,重量分别为G A 和G B 的物体重叠地放置在粗糙的水平面上,水平力P 作用于物体A上,设A 、B 间的摩擦力的最大值为max A F ,B 与水平面间的摩擦力的最大值为max B F ,若A 、B 能各自保持平衡,则各力之间的关系为( )。
① max max B A F F P >>② max max B A F F P <<③ max max A B F P F >>④ max max B A F P F <<4.如图所示,物体A 重力的大小为100kN ,物体B 重力的大小为25kN ,A 与地面间的摩擦系数为0.2,滑轮处摩擦不计。
则物体A 与地面间的摩擦力为( )。
① 20kN② 16kN③ 15kN④ 12kN① F = 0 ② F 水平向右,且F = G ③ F 沿斜面向上,且F = G ① ②③④ ⑤⑥5.如图所示,当左右两木板所受的压力均为F 时,物体A夹在木板中间静止不动。
若两端木板所受压力各为2F ,则物体A 所受到的摩擦力为( )。
① 与原来相等② 是原来的两倍③ 是原来的四倍6.如图所示,已知重物重量为P = 100N ,用力F = 500N 的压力压在一铅直面上,其摩擦系数s f = 0.3,则重物受到的摩擦力为( )。
① 150kN② 100kN③ 500kN④ 30kN7.一物块重量为P ,放在倾角为α的斜面上,如图所示,斜面与物块间的摩擦角为m ϕ,且αϕ>m 。
今在物块上作用一大小也等于P 的力,则物块能在斜面上保持平衡时力P 与斜面法线间的夹角β的最大值应是( )。
a
A
y
D
q
南京航空航天大学
2012年硕士研究生入学考试初试试题( A 卷)
科目代码: 815 科目名称: 理论力学 满分: 150 分
注意:①认真阅读答题纸上的注意事项;②所有答案必须写在答题纸上,写在本试题纸或草稿纸上均无效;③本试题纸须随答题纸一起装入试题袋中交回!
815 理论力学第 1 页共 2 页
815 理论力学第 2 页共 2 页
南京航空航天大学
2013年硕士研究生入学考试初试试题( A 卷)
科目代码: 815 科目名称: 理论力学 满分: 150 分
注意:①认真阅读答题纸上的注意事项;②所有答案必须写在答题纸上,写在本试题纸或草稿纸上均无效;③本试题纸须随答题纸一起装入试题袋中交回!
科目代码:815 科目名称:理论力学第 1 页共 2 页
科目代码:815 科目名称:理论力学第 2 页共 2 页。
南京航空航天大学2016年硕士研究生招生考试初试试题(A 卷 )科目代码: 917满分: 150分科目名称:工程热力学(专业学位)注意: ①认真阅读答题纸上的注意事项;②所有答案必须写在答题纸上,写在本试题纸或草稿纸上均无效;③本试题纸须随答题纸一起装入试题袋中交回!一、简答题(60分)1. (5分)有人认为一个物体的温度越高,其含有的热量越高,因此能够对外做出更多的功。
请就此观点进行简要分析。
2. (5分)试判定比体积、比热力学能、比焓、比熵以及比热这5个参数,哪些是状态参数?3. (5分)不可逆过程就是指工质不能恢复到初始状态的热力过程。
请简要分析该说法是否正确。
4. (5分)如图1所示,有任意两个热力过程a-b 和a-c 。
假设b 和c 点处于同一个绝热等熵线上,请分析和判定ab U ∆和ac U ∆的大小关系。
图15. (5分)现有1kg 的某理想气体,其温度同环境温度相同。
有人认为由于其温度同环境温度一致,因此该理想气体的热力学能为零,并无法对外输出功。
请简要分析该观点是否正确。
6. (5分)气体在喷管内绝热流动,无论是否可逆,出口速度都可以用()2022f c h h =-来计算,这是否意味着可逆过程和不可逆过程所得到的效果是相同的?请简要分析。
假设忽略进出口势能差。
7. (6分)理想气体流经某绝热节流装置,节流前温度为300K ,压力为1MPa ,节流后压力降低为0.7MPa 。
请分析节流后该气体的温度是大于、小于还是等于300K 。
假设忽略进出口的动能和势能变化。
8. (6分)某绝热储气罐内,存储有温度为25℃的空气。
试预估当储气罐内压力处于什么范围时,打开放气阀排气,会在阀门附近出现结冰的现象?假设环境压力为0.1MPa ,相对湿度不为零。
9. (8分)某可逆正向循环如图2所示,过程1-2为温度随熵线性变化的过程,过程2-3为等熵过程,过程3-1是等温过程。
试求该循环的热效率。
南航理论力学11考研真题1.动量定理适用于( ).①惯性坐标系②与地球园连的坐标系③相对于地球作匀角速转动的坐标系④粗对于地球作匀速直线运动的坐标系正确答案:①2.质点系动量守恒的条件是( ).①作用于质点系的外力主矢恒等于零②作用于质点系的内力主矢恒等于零③作用于质点系的约束反力主矢恒等于零④作用于质点系的主动力主矢恒等于零正确答案:①3.弹球铅重落地并弹回,设落地和弹回瞬时的速度大小均为v.则地面反力冲量的大小/( ).①1-0②/-mv③1-2mv④因碰地时间未知,故无法计算正确答案:③p A>p B③p₁“p₂④不能确定正确答案:●正确答案:③4.两个完全相同的圆盘,放在光滑水平面上,如图所示。
在两个圆盘的不同位置上,分别作用两个相同的力F和P,设两圆盘从静止开始运动。
某瞬时两圆盘动量p,和pa的关系是( ).p₁<p₁5.匀质杆AB重G,其A端置于光滑水平面上,B端用绳子悬挂,如图所示。
取坐标系Oxy,此时该杆质心C的x坐标x=θ若将图子剪断,则( ).①杆倒向地面的过程中,其质心C运动的轨迹为圆弧②杆倒至地面后,xC>0③杆倒至地面后,xC=0④杆倒至地面后,xC<0正确答案:①③K=8.72Ns④K-4Ns正确答案:①正确答案:④6. 图示四连杆机构中,各均质杆长度为O₁A=O₂B=AB=20cm,它们的质量相等,均为m=1kg₋在图示瞬时,OAA杆转动的角速度ω=√2rad/8,O1A与O₂B两杆的倾角均为45ᵇ,此时该机构的动量K大小为( ).①K-0.4Ns②K-0.483 Ns③K-0.6Ns④K=0.766Ns所示,已知圆盘的质量m=20kg, 半径R=10cm,在图示位置时,OA杆的倾角为30°,其转角的角速度m=1 rad%。
固盘相对于 OA杆转动的角速度ω2=4md2s,OB=10√3cm,则此时圆盘的动量K大小为( ).K=6.93N⋅②K-8Ns8.图示平面四连杆机构中,曲柄O₁A、O₂B 和连杆AB皆可视为质量为为ω,则该阶时此系统的动量为( ).①2mwd②3mmd③4mod④6mmd正确答案:③9.图示平面机构中,物块A的质量为m,可沿水平直线轨道滑动;均质杆AB 的质量为m₁,长为21,其A端与物块铰接,B端圆连一质量为m,的重质点。
梦想不会辜负每一个努力的人
南京航空航天大学
2016年硕士研究生招生考试初试试题(A卷)科目代码:860
满分:150 分
科目名称:道路工程材料
注意:①认真阅读答题纸上的注意事项;②所有答案必须写在答题纸上,写在本试题纸或草稿纸上均无效;③本试题纸须随答题纸一起装入试题袋中交回!
一、简答题(每题5分,共30分)
1.1 胶凝材料及分类?
1.2 引起水泥体积安定性不良的原因?
1.3 石油沥青针入度?
1.4 钢材的锈蚀和防锈?
1.5 预防混凝土的碱-骨料反应措施?
1.6 石灰的熟(消)化的特点?
二、论述题(每道题20分,共120分)
2.1 论述普通混凝土对骨料的技术质量要求?
2.2 论述SBS(丁苯橡胶)改性沥青特点?
2.3 道路硅酸盐水泥特点?
2.4 混凝土的碳化?对钢筋混凝土性能有哪些影响?
2.5 论述钢材的拉伸性能?
2.6 硬化混凝土的变形性能?
科目代码:860科目名称:道路工程材料第1页共1页。