下载文档原格式
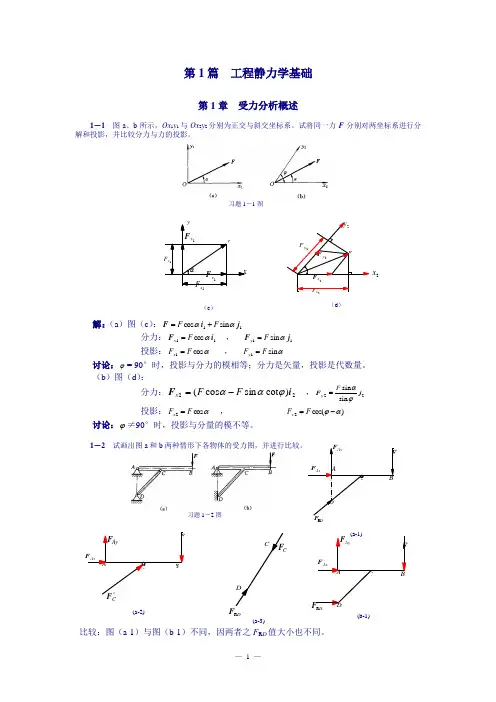
C(a-2)DR(a-3)(b-1)DR第1篇 工程静力学基础第1章 受力分析概述1－1 图a 、b 所示，Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一力F 分别对两坐标系进行分解和投影，并比较分力与力的投影。
习题1－1图解：（a ）图（c ）：11 s i n c o s j i F ααF F +=分力：11 cos i F αF x = ， 11 s i n j F αF y =投影：αcos 1F F x = ， αs i n 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
（b ）图（d ）： 分力：22)cot sin cos (i F ϕααF F x -= ，22sin sin j F ϕαF y = 投影：αcos 2F F x = ， )cos(2αϕ-=F F y讨论：ϕ≠90°时，投影与分量的模不等。
1－2 试画出图a 和b习题1－2图比较：图（a-1）与图（b-1）不同，因两者之F R D 值大小也不同。
（c ）2x（d ）1－3 试画出图示各物体的受力图。
习题1－3图B或(a-2)(a-1)(b-1)F(c-1) 或(b-2)(e-1)F(a)1－4图a 所示为三角架结构。
荷载F 1作用在铰B 上。
杆AB 不计自重，杆BC 自重为W 。
试画出b 、c 、d 所示的隔离体的受力图，并加以讨论。
习题1－4图1－5图示刚性构件ABC 由销钉A 和拉杆D 支撑，在构件C 点作用有一水平力F 。
试问如果将力F 沿其作用线移至D 或E （如图示），是否会改为销钉A 的受力状况。
解：由受力图1－5a ，1－5b 和1－5c 分析可知，F 从C 移至E ，A 端受力不变，这是因为力F 在自身刚体ABC 上滑移；而F 从C 移至D，则A 端受力改变，因为HG 与ABC 为不同的刚体。
1(f-1)'A(f-2)1(f-3)F F'F 1(d-2)AF yB 21(c-1)F A B1FDx y(b-2)1(b-3)F yB 2 F A B1B F习题1－5图AxF'(b-3)E D(a-3)B(b-2)(b-1)F 'CDDF EFBC(c)AxF1－6 试画出图示连续梁中的AC 和CD 梁的受力图。
2014年10月10日基础部分——静力学第2 章力系的等效与简化力系分类：平面力系空间力系第2章力系的等效和简化力在平面上的投影F xy矢量力在坐标轴上的投影z标量？o90=γzzF xyϕ（二次投影法（二次投影法）（一次投影法（一次投影法）ik jkj i F z y x F F F ++=OxyAF思考：投影与分力间的联系？k j i F z y x F F F ++=zy x F F F F ++=ik j即：对正交坐标系，分力的大小和投影的大小相等。
？即代数和合力投影定理合力投影定理⎪⎭⎪⎬⎫2-1-1 力对点之矩（力矩）xy zOhz)y,A(x,BF矢量r 即矩心z z)(F MOxyzOhz)y,A(x,BFr矩心)(F M O zz)(F M O z定位矢zyxF F F z y x k j i ikjxyzOhz)y,A(x,BFr矩心)(F M OzyxF F F z y x k j i y z z x ？0,0==z F z定义zz代数量力F 对z 轴的矩2-1-2 力对轴之矩力对轴之矩是力使物体绕某一轴F xy在什么情况下M Oz (F )= 0?[思考]0F平行于z 轴F通过z轴)(FOzM hFxy±=当力与轴共面时，力对该轴之矩等于零。
解析表达式另定义xyzOhz)y,A(x,BFr)(F M O )(F Oz M []zO )(F M =力对点之矩与力对轴之矩的关系?[例2-1] xyzOA BFxyF [解法1] 按定义计算[解法2] 按解析式计算2)0,,(a a FF F F F z y x 22,22,0=−==22?)(=F Ox M ?)(=F Oy M2-1-3 合力矩定理定理矢量和点合力矩定理z汇交力系存在合力；那其它力系呢？z轴合力矩定理[例2-2] O )(F M ？[]ααsin cos )(231l l l F −−解：合力矩定理平面力对点之矩OAr yF xF ?=d如何判断两力系等效？M CF BF A力系1F CM EM D力系22-2-1 力系的特征量——主矢与主矩主矢力系中所有力的矢量和。
eBook材料力学习题详细解答教师用书(第13章)2006-01-18范 钦 珊 教 育 教 学 工 作 室FAN Qin-Shan’s Education & Teaching Studio习题13－1 习题13－2 习题13－3 习题13－4 习题13－5 习题13－6 习题13－7 习题13－8第13章 动载荷与疲劳强度概述13－1 图示的No.20a 普通热轧槽钢以等减速度下降，若在0.2s 时间内速度由1.8m/s 降至0.6m/s ，已知l =6m ，b =1m 。
试求槽钢中最大的弯曲正应力。
解：No.20a 槽钢的线密度63.22=ρkg/m槽钢的加速度62.08.16.0−=−=a m/s 2 由自重引起的均布载荷集度：g q ρ=1(↓)由惯性力引起的均布载荷集度： a q ρ=2(↓) (加速度↑)总的均布载荷集度：)(21a g q q q +=+=ρ由总载荷（动载荷＋静载荷）引起的弯矩：)(4432824max a g q q q M M C +=×=××+××−==ρ=4×22.63(9.8+6)=1430 N ·m于是，槽钢横截面上的最大正应力MPa 1591022414306min dmax ..=×==−W M C σ13－2 钢制圆轴AB 上装有一开孔的匀质圆盘如图所示。
圆盘厚度为δ，孔直径300mm 。
圆盘和轴一起以匀角速度ω转动。
若已知：δ=30mm ，a =1000mm ，e =300mm；轴习题13－1图习题13－2图直径d =120mm ，ω=40rad/s ；圆盘材料密度33m kg 108.7×=ρ。
试求由于开孔引起的轴内最大弯曲正应力（提示：可以将圆盘上的孔作为一负质量（-m ），计算由这一负质量引起的惯性力）。
解：将圆盘上的孔作为一负质量（-m ），计算由这一负质量引起的惯性力：222I π4F me D e ==××××ωρδω由此引起的附加动约束力：2IF F F B A == 动载荷引起的附加最大动弯矩发生在C 截面，其值为：a F a F M A I max 21== 于是，最大附加弯曲动应力：22dmax dmax 3π24672MPa π32.a D e M d W⋅⋅===ρδωσ13－3 质量为m 的匀质矩形平板用两根平行且等长的轻杆悬挂着，如图所示。
