清华大学范钦珊版理论力学复习材料-第1章
- 格式:ppt
- 大小:4.73 MB
- 文档页数:79



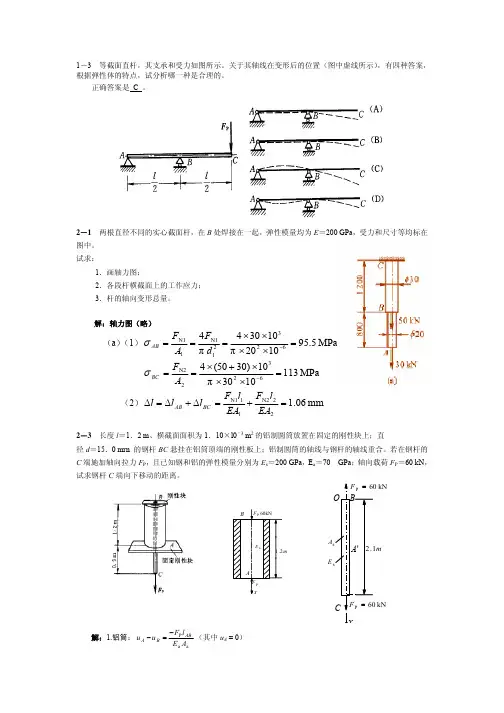
习题1-1图 习题1-2图习题1-3图习题1-4图习题1-5图习题1-6图 材料力学习题集第1章 引 论1-1 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M 。
关于固定端处横截面A -A 上的内力分布,有四种答案,根据弹性体的特点,试分析哪一种答案比较合理。
正确答案是 C 。
1-2 图示带缺口的直杆在两端承受拉力F P 作用。
关于A -A 截面上的内力分布,有四种答案,根据弹性体的特点,试判断哪一种答案是合理的。
正确答案是 D 。
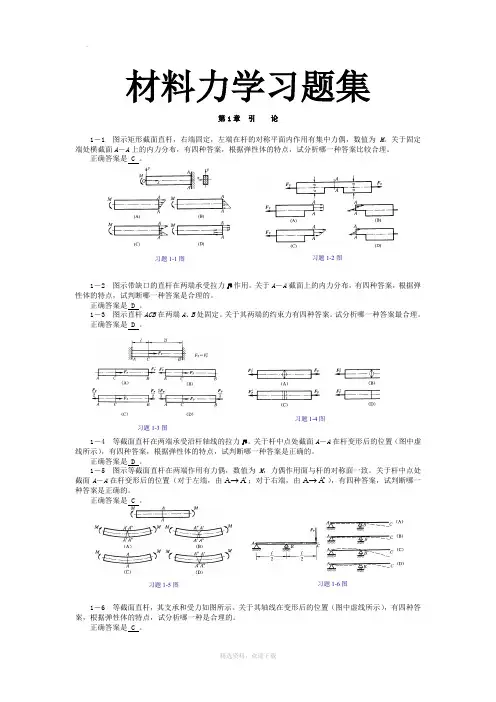
1-3 图示直杆ACB 在两端A 、B 处固定。
关于其两端的约束力有四种答案。
试分析哪一种答案最合理。
正确答案是 D 。
1-4 等截面直杆在两端承受沿杆轴线的拉力F P 。
关于杆中点处截面A -A 在杆变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试判断哪一种答案是正确的。
正确答案是 D 。
1-5 图示等截面直杆在两端作用有力偶,数值为M ,力偶作用面与杆的对称面一致。
关于杆中点处截面A -A 在杆变形后的位置(对于左端,由A A '→;对于右端,由A A ''→),有四种答案,试判断哪一种答案是正确的。
正确答案是 C 。
1-6 等截面直杆,其支承和受力如图所示。
关于其轴线在变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试分析哪一种是合理的。
正确答案是 C 。
习题2-1图习题2-2图习题2-3图习题2-4图ABABC)(ql 2lM QF QF 454141第2章 杆件的内力分析2-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A ))(d d Q x q x F =;Q d d F x M=; (B ))(d d Q x q x F -=,Q d d F x M-=; (C ))(d d Q x q x F -=,Q d d F x M=; (D ))(d d Q x q x F =,Q d d F xM-=。



绪论理论力学运动机械运动运动变形机械运动 材料力学变形理论力学的局限性:¾¾相对论力学量子力学多数工程问题都是适用的。
z 远小于光速z 宏观20世纪以前 20世纪中例如:金茂大厦楼高420.5m共88 层中庭楼高492m 地上101层,地下3层上海环球金融中心台北101 (Taipei 101)楼高508 m地上101层,地下5层建筑高632m上海中心大厦哈利法塔楼高?(迪拜塔)828m紫峰大厦(Zifeng Tower)楼高450 m地上89层,地下3层浦东开发区桥面结构立柱与缆索桥面结构立柱与缆索上海南浦大桥垮塌前的大桥垮塌后的大桥法庭以外的问题力学素质的重要性简单力学问题高等力学问题脚上的力量假设人体重量为750N 3000N 3500N 4500N 6000N12500N•单跨双曲石拱桥•不用一根钢筋•一千四百多年依然能承受数吨汽车直道弯道连接直接连接缓和弯道长征火箭家族长征三号乙“神舟”五号载人飞船发射升空“神舟”七号载人飞船发射升空Space Shuttle Discovery发现号日挑战者号发射升空原因:O形密封圈泄漏。
日哥伦比亚号重返大气层时解原因:起飞时隔热泡沫塑料脱落,撞坏机翼。
交会对接神九飞船天宫一号太阳能电池帆板车头车身长江三峡工程荷兰拦海大坝坝宽?32公里力学¾¾z若已知推力和跑道可能长度,则需要多大的初速度和一定的时间间隔后才能达到飞离甲板时的速度。
z若已知初速度、一定的时间间隔后飞离甲板时的速度,则需要弹射器施加多大推力,或者确定需要多长的跑道。
目标与雷达之间的距离雷达方位角速度加速度。

2014年10月10日基础部分——静力学第2 章力系的等效与简化力系分类:平面力系空间力系第2章力系的等效和简化力在平面上的投影F xy矢量力在坐标轴上的投影z标量?o90=γzzF xyϕ(二次投影法(二次投影法)(一次投影法(一次投影法)ik jkj i F z y x F F F ++=OxyAF思考:投影与分力间的联系?k j i F z y x F F F ++=zy x F F F F ++=ik j即:对正交坐标系,分力的大小和投影的大小相等。
?即代数和合力投影定理合力投影定理⎪⎭⎪⎬⎫2-1-1 力对点之矩(力矩)xy zOhz)y,A(x,BF矢量r 即矩心z z)(F MOxyzOhz)y,A(x,BFr矩心)(F M O zz)(F M O z定位矢zyxF F F z y x k j i ikjxyzOhz)y,A(x,BFr矩心)(F M OzyxF F F z y x k j i y z z x ?0,0==z F z定义zz代数量力F 对z 轴的矩2-1-2 力对轴之矩力对轴之矩是力使物体绕某一轴F xy在什么情况下M Oz (F )= 0?[思考]0F平行于z 轴F通过z轴)(FOzM hFxy±=当力与轴共面时,力对该轴之矩等于零。
解析表达式另定义xyzOhz)y,A(x,BFr)(F M O )(F Oz M []zO )(F M =力对点之矩与力对轴之矩的关系?[例2-1] xyzOA BFxyF [解法1] 按定义计算[解法2] 按解析式计算2)0,,(a a FF F F F z y x 22,22,0=−==22?)(=F Ox M ?)(=F Oy M2-1-3 合力矩定理定理矢量和点合力矩定理z汇交力系存在合力;那其它力系呢?z轴合力矩定理[例2-2] O )(F M ?[]ααsin cos )(231l l l F −−解:合力矩定理平面力对点之矩OAr yF xF ?=d如何判断两力系等效?M CF BF A力系1F CM EM D力系22-2-1 力系的特征量——主矢与主矩主矢力系中所有力的矢量和。
第一篇静力学工程力学是范围较大的一门学科,涉及静力学、运动学、动力学、材料力学等方面的知识,是诸多工程技术的研究基础,在工程实际应用中起着重要的基础学科作用。
本篇根据高职教育的特点,只对部分知识作一简单介绍,为学习机械原理与机械零件、机械制造技术及相关专业技术奠定必要的基础,主要介绍工程静力学的基础内容。
第1章静力学基础本章要点●掌握力、刚体、平衡和约束的概念●掌握静力学公理●掌握约束的基本特征及约束反力的画法●掌握单个物体与物体系统的受力分析及受力图。
●掌握力多边形法则及平面汇交力系合成与平衡的几何条件1.1 力和力矩1.1.1 力的概念力的概念产生于人类从事的生产劳动当中。
当人们用手握、拉、掷及举起物体时,由于肌肉紧张而感受到力的作用,这种作用广泛存在于人与物及物与物之间。
例如,奔腾的水流能推动水轮机旋转,锤子的敲打会使烧红的铁块变形等。
1.力的定义力是物体之间相互的机械作用,这种作用将使物体的机械运动状态发生变化,或者使物体产生变形。
前者称为力的外效应;后者称为力的内效应。
2.力的三要素实践证明,力对物体的作用效应,决定于力的大小、方向(包括方位和指向)和作用点的位置,这三个因素就称为力的三要素。
在这三个要素中,如果改变其中任何一个,也就改变了力对物体的作用效应。
例如:用扳手拧螺母时,作用在扳手上的力,因大小不同,或方向不同,或作用点不同,它们产生的效果就不同(图1-1a)。
1.1.2 作用在刚体上的力的效应与力的可传性力是一个既有大小又有方向的量,而且又满足矢量的运算法则,因此力是矢量(或称向量)。
矢量常用一个带箭头的有向线段来表示(图1-1b),线段长度AB按一定比例代表力的大小,线段的方位和箭头表示力的方向,其起点或终点表示力的作用点。
此线段的延伸称为力的作用线。
用黑体字F代表力矢,并以同一字母的非黑体字F代表该矢量的模(大小)。
4.力的单位力的国际制单位是牛顿或千牛顿,其符号为N,或kN。
材料力学课后答案范钦珊普通高等院校基础力学系列教材包括“理论力学”、“材料力学”、“结构力学”、“工程力学静力学材料力学”以及“工程流体力学”。
目前出版的是前面的3种“工程力学静力学材料力学”将在以后出版。
这套教材是根据我国高等教育改革的形势和教学第一线的实际需求由清华大学出版社组织编写的。
从2002年秋季学期开始全国普通高等学校新一轮培养计划进入实施阶段新一轮培养计划的特点是加强素质教育、培养创新精神。
根据新一轮培养计划课程的教学总学时数大幅度减少为学生自主学习留出了较大的空间。
相应地课程的教学时数都要压缩基础力学课程也不例外。
怎样在有限的教学时数内使学生既能掌握力学的基本知识又能了解一些力学的最新进展既能培养学生的力学素质又能加强工程概念。
这是很多力学教育工作者所共同关心的问题。
现有的基础教材大部分都是根据在比较多的学时内进行教学而编写的因而篇幅都比较大。
教学第一线迫切需要适用于学时压缩后教学要求的小篇幅的教材。
根据“有所为、有所不为”的原则这套教材更注重基本概念而不追求冗长的理论推导与繁琐的数字运算。
这样做不仅可以满足一些专业对于力学基础知识的要求而且可以切实保证教育部颁布的基础力学课程教学基本要求的教学质量。
为了让学生更快地掌握最基本的知识本套教材在概念、原理的叙述方面作了一些改进。
一方面从提出问题、分析问题和解决问题等方面作了比较详尽的论述与讨论另一方面通过较多的例题分析特别是新增加了关于一些重要概念的例题分析著者相信这将有助于读者加深对于基本内容的了解和掌握。
此外为了帮助学生学习和加深理解以及方便教师备课和授课与每门课材料力学教师用书lⅣ程主教材配套出版了学习指导、教师用书习题详细解答和供课堂教学使用的电子教案。
本套教材内容的选取以教育部颁布的相关课程的“教学基本要求”为依据同时根据各院校的具体情况作了灵活的安排绝大部分为必修内容少部分为选修内容。
每门课程所需学时一般不超过60。
范钦珊2004年7月于清华大学前言为了减轻教学第一线老师不必要的重复劳动同时也为了给刚刚走上材料力学教学岗位的青年教师提供教学参考资料我们将“材料力学”教材中全部习题作了详细解答编写成册定名为“材料力学教师用书”。
C(a-2)DR(a-3)(b-1)DR第1篇 工程静力学基础第1章 受力分析概述1-1 图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一力F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
习题1-1图解:(a )图(c ):11 s i n c o s j i F ααF F +=分力:11 cos i F αF x = , 11 s i n j F αF y =投影:αcos 1F F x = , αs i n 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
(b )图(d ): 分力:22)cot sin cos (i F ϕααF F x -= ,22sin sin j F ϕαF y = 投影:αcos 2F F x = , )cos(2αϕ-=F F y讨论:ϕ≠90°时,投影与分量的模不等。
1-2 试画出图a 和b习题1-2图比较:图(a-1)与图(b-1)不同,因两者之F R D 值大小也不同。
(c ) 22x(d )1-3 试画出图示各物体的受力图。
习题1-3图B或(a-2)B(a-1)(b-1)F(c-1) 或(b-2)(e-1)F(a)1-4 图a 所示为三角架结构。
荷载F 1作用在铰B 上。
杆AB 不计自重,杆BC 自重为W 。
试画出b 、c 、d 所示的隔离体的受力图,并加以讨论。
习题1-4图1-5 图示刚性构件ABC 由销钉A 和拉杆D 支撑,在构件C 点作用有一水平力F 。
试问如果将力F 沿其作用线移至D 或E (如图示),是否会改为销钉A 的受力状况。
解:由受力图1-5a ,1-5b 和1-5c 分析可知,F 从C 移至E ,A 端受力不变,这是因为力F 在自身刚体ABC 上滑移;而F 从C 移至D,则A 端受力改变,因为HG 与ABC 为不同的刚体。
1(f-1)'A(f-2)1O(f-3)F F'F 1(d-2)F yB 21(c-1)F A B1B FDx y(b-2)1(b-3)F yB 2 A A B1B F习题1-5图AxF(b-3)E D(a-3)B(b-2)(b-1)F 'CBC(c)AxF1-6 试画出图示连续梁中的AC 和CD 梁的受力图。