当前位置：文档之家 › 李雅普诺夫稳定性理论 (2)

李雅普诺夫稳定性理论 (2)

  • 格式：ppt
  • 大小：1016.50 KB
  • 文档页数：40

下载文档原格式

  / 40

合集下载

李雅普诺夫稳定性分析方法-文档资料

李雅普诺夫稳定性分析方法-文档资料

用泰勒展开,并取到一 次项,忽略高次项,故有 x 2 s i n x x 0 2 2 x 0 x s i n x 0 c o s x 0 x
• 从而有
y a y b y 0 b y x 0 2 s i n x 0 ( 2 x 0 c o s x 0 ) x
1.自治系统
• 定义地:自治系统定义为不受外部影响即没 有输入作用的一类系统.
• 一般情形的系统描述: x f(x ,t),x (t0 ) x 0 ,t [t0 , ] • 线性时变系统的描述: x A (t)x ,x (t0 ) x 0 ,t t0 , • 线性时不变的描述: xA x ,x (t0 ) x 0 ,t [t0 , )
• 则有
y(s)2x0cosx0 x(s) s2asb
G(s)
• 故线性模型G(s)描述了非线性方程在 x 0 处 x 和 y 的运动特性,而Laypunov第一方法, 则是根据G(s)的特征值来分析其在小扰动 范围内运动稳定性.
（2）李雅普诺夫第二方法
• 也称直接法,属于直接根据系统结构判断内 部稳定性的方法.
一.系统运动稳定性的性质.
• 运动稳定性的实质,归结为系统平衡状态的 稳定性.
• 平衡状态的稳定性问题实际就是:偏离平衡 状态的受扰运动能否只依靠系统内部的结 构因素,或者使之限制在平衡状态的有限临 域内,或者使之同时返回平衡状态.
• 从而要讨论三个重要概念:
1.自治系统. 2.平衡状态. 3.受扰运动.
• 显然 by0x02sinx0代入后,得到
y a y b y ( 2 x 0 c o s x 0 ) x
• 两边进行拉氏变换得(初始状态 y0 0 ),则
现代控制理论习题之李雅普诺夫稳定判据

现代控制理论习题之李雅普诺夫稳定判据


⎧ 1 = − x1 + x 2 + x1 ( x1 2 + x 2 2 ) ⎪x (2) ⎨ 2 = − x1 − x 2 + x 2 ( x1 2 + x 2 2 ) ⎪ ⎩x
【解】 ： （1）采用非线性系统线性化的方法，在平衡点原点处线性化得：
A= ∂f ∂x T ⎡ ∂f 1 ⎢ ∂x =⎢ 1 ⎢ ∂f 2 ⎢ ∂x ⎣ 1 ∂f 1 ⎤ ⎡1 − 3 x1 2 ⎡1 − 1⎤ −1 ⎤ ∂x 2 ⎥ ⎥ =⎢ =⎢ ⎥ 2⎥ ∂f 2 ⎥ 1 − 3x 2 ⎦ ⎢ 1 ⎥ x = 0 ⎣1 1 ⎦ ⎣ ∂x 2 ⎥ ⎦ x =0
t − t0 = − 1 1 0.05 v ( x, t ) =− ln = 10.955 v( x0 , t0 ) λ2 100
ηmin
ln
4-7
试确定下列非线性系统在原点处的稳定性。
6
第四章
Lyapunov 稳定性理论
⎧ 1 = x1 − x 2 − x1 3 ⎪x (1) ⎨ 2 = x1 + x 2 − x 2 3 ⎪ ⎩x
0.5 1
= 0.75 > 0 ， 0.5 0.5
v( x) = x T Px 正定。 ∆v (k ) = x T (k )(G T PG − P ) x (k )
3 0⎤ ⎡1 3 0⎤ ⎡1 − 3 1⎤ ⎡ 1 0.5 0.5⎤ ⎡ 1 ⎥ ⎢− 3 − 2 − 3⎥ − ⎢− 3 − 2 − 3⎥ ⎥ ⎢0.5 1 G T PG − P = ⎢ 3 − 2 0 0 ⎥ ⎥ ⎢ ⎥⎢ ⎥⎢ ⎢ ⎢ 1⎥ 0 0⎥ 0 0⎥ ⎦ ⎣1 ⎦ ⎢ ⎣1 ⎦⎢ ⎣0.5 0 ⎦⎢ ⎣0 − 3 0 ⎥ ⎡ 8 4.5 7 ⎤ ⎥ =⎢ ⎢4.5 6 1.5⎥ ⎢ 7 1.5 8 ⎥ ⎦ ⎣ 8 4.5 7
李雅普诺夫第二法

李雅普诺夫第二法


12/23/2012
2 V ( x) ( x1 x2 )( x1 x2 ) 2x1x1 x2 x2 ( x12 x2 )
当 x 时， ( x) ，所以系统在其原点处大范围 V 渐近稳定。
12/23/2012
4.3 李雅普诺夫第二法
x1 x1 x2 例4-8 系统的状态方程为 x2 x1 x2
,
,
可见此二次型函数是正定的，即
12/23/2012
4.3 李雅普诺夫第二法
4.3.2 几个稳定性判据 定理 设系统的状态方程为
x f ( x),
如果平衡状态 xe 0, 即， f ( xe ) 0 如果存在标量函数V(x) 满足：
1） V ( x) 对所有x具有一阶连续偏导数。 2） V ( x) 是正定的；
12/23/2012
4.3 李雅普诺夫第二法
例 设 x x1
x2
x3
T
2 1) V ( x) ( x1 x2 )2 x3
因为V（0） 0，而且对非零向量 ，有x a，a， T 0, x （ - 0） 也使V（x） 0，所以V（x）是半正定的。
2 2) V ( x) x12 x2因为V（0） 0，而且对非零向量 ，有x 0， a） 0, x （ 0， T 也使V（x） 0，所以V（x）是半正定的。
12/23/2012
4.3 李雅普诺夫第二法
2. 二次型标量函数
设 x1，x2 ，xn为n个变量， 二次型标量函数可写为
p11 p V ( x) xT Px x1 x2 xn 21 pn1 其中，P为实对称矩阵。 p12 p22 p1n x1 x2 pnn xn
现代控制理论第四章-李雅普诺夫稳定性

现代控制理论第四章-李雅普诺夫稳定性


0s
0
1
s
0 1 1 1 1
(s
s 1 1)(s 1)
s
1 1
可见传递函数的极点 s 1位于s的左半平面，故系统
输出稳定。这是因为具有正实部的特征值2 1 被系统的零
点 s 1 对消了，所以在系统的输入输出特性中没被表现出
来。由此可见，只有当系统的传递函数W(s)不出现零、极
点对消现象，并且矩阵A的特征值与系统传递函数W(s)的
2020/3/22
6
现代控制理论
第4章 李亚普诺夫稳定性分析
4.2 李亚普诺夫第二法的概述
1892年俄国学者李亚普诺夫发表了《运动稳定性一般 问题》，最早建立了运动稳定性的一般理论，并把分析常 微分方程组稳定性的全部方法归纳为两类。第一类方法先 求出常微分方程组的解，而后分析其解运动的稳定性，称 为间接方法；第二类方法不必求解常微分方程组，而是提 供出解运动稳定性的信息，称为直接方法，它是从能量观 点提供了判别所有系统稳定性的方法。
即Xe f ( X e ,t) ，0 则把 叫X e做系统的平衡状态。
对于线性定常系统 X AX而言，其平衡状态满足
Xe AX e ，0 若A是非奇异矩阵，则只有 X e ，0 即对线性系 统而言平衡状态只有一个，在坐标原点；反之，则有无限
多个平衡状态。
对于非线性系统而言，平衡状态不只一个。
2020/3/22
9
现代控制理论
第4章 李亚普诺夫稳定性分析
3、李亚普诺夫第二法
李亚普诺夫第二法建立在这样一个直观的物理事实上：
如果一个系统的某个平衡状态是渐近稳定的，即
im
t
X
X，e 那么随着系统的运动，其储存的能量将随时间
李雅普诺夫第二方法简介

李雅普诺夫第二方法简介


定义1: 假设V(x)为在域x H内定义的一个连续函数,
V(0)0. (1)如果在此域内恒有V(x)0,则称函数V为半正定. (2)如果对一切x0,都有V(x)0,称函数V为正定. （3）如果函数V是定正(半正定), 则称函数V是负定(半负定).
例 V(x1，x2 ) x12 x22 2x1x2 半正定
x2
u2
u1
v0
ε x1
u3
例:考虑如下系统关于零解的稳定性： x 5x
首先构造一个正定函数：
V (x ) x 2
显 然 ， V ( x ) 0 x 0 ,且 V ( x ) 0 x 0 。
现 在 ， 我 们 考 虑 V 沿 上 述 微 分 方 程 的 解 对 时 间 t的 导 数 ， 有
x 1 2(t) x2 2(t) x 1 2(t0) x2 2(t0)。
例：考虑小阻尼线性振动系统：
x1 x 2 x 2 x1 x 2
研 究 其 平 衡 状 态 x 1 0 , x 2 0 的 稳 定 性 。 若 取 v(x)x1 2x2 2,则 有
v x v 1 x 1 x v 2 x 2 2 x 1 x 2 2 x 2 ( x 1 x 2 ) 2 x 2 2 0
V(x, y) x y2 y2.
正定
V(x, y) 1 y2 g (1 cos x). 2l
正定
V(x, y) ax2 bxy cy2
a 0, 4ac b2 0.
a 0,
4ac b2 0.
V(x, y) 1 y2 x g(s)ds,
2
0
xg(x) 0.
正定 负定
V (x1,x2)3 x1 22 x1 x22 x2 2
易于验证，这是一个正定函数。
李雅普诺夫稳定性分析(二)

李雅普诺夫稳定性分析(二)


由于变换后的对角线矩阵的对角线上的元素都大 于零，故矩阵P为正定的。因此，系统为大范围 渐近稳定的。 此时，系统的李雅普诺夫函数和它沿状态轨线对 时间t的全导数分别为
1 T 3 1 V ( x ) = x Px = x x > 0 2 1 2 0 T T − 1 V ′(x) = −x Qx = x x < 0 0 − 1
T
例5-10 控制系统方块图如下图所示。 要求系统渐近稳定，试确定增益的取值范围。
x3
k s +1
1 s+2
x2
1 s
x1
-
解: 由图可写出系统的状态方程为 ɺ 1 0 x1 x1 0 x = 0 x ɺ2 −2 1 2 x3 − k 0 − 1 x 3 ɺ
例5-9 试确定用如下状态方程描述的系统的平衡态稳 定性。 ′ x1 0 1 x1 x′ = − 1 − 1 x 2 2 解: 设选取的李雅普诺夫函数为 V(x)=xTPx 由定理5-7可知，上式中的正定矩阵P满足李雅普 诺夫方程 PA+ATP=-I. 于是，令对称矩阵P为
由于V’(x)正半定，但其只在x1=0，x2=0时才恒为零， 而在其他状态不恒为零，因此由定理5-6的2)可知， 系统的该平衡态为不稳定的。
下面将前面讨论的李雅普诺夫稳定性的判定方法 作一小结
V(x) 正定(>0) V’(x) 负定(<0) 结论 该平衡态渐近稳定
负半定(≤0)且不恒为0 正定(>0) 该平衡态渐近稳定 (对任意非零的初始状态的解) 正定(>0) 正定(>0) 正定(>0) 负半定(≤0)且恒为0 (对某一非零的初始状态的解) 正定(>0) 该平衡态稳定 但非渐近稳定 该平衡态不稳定
李雅普诺夫Lyapunov稳定性理论李雅普诺夫

李雅普诺夫Lyapunov稳定性理论李雅普诺夫


现代控制理论的稳定性判据
李雅普诺夫（Lyapunov）稳定性理论
李雅普诺夫（Lyapunov）稳定性理论
李雅普诺夫，俄国数学力学专家， 俄罗斯科学院院士，意大利林琴 科学院 以及法国巴黎科学院的外籍院士。 1892年在他的博士论文《运动稳定性的一般 问题》（The general problem of the stability motion） 中系统地研究了由微分方程描述的一般运动系统的稳定性 问题，建立了著名的Lyapunov方法，为现代控制和非线性 控制奠定了基础。 Lyapunov稳定性理论对于控制理论学科的发展产生了深刻 的影响，已成为现代控制理论的一个非常重要的组成部分。
时，从任意初态出发的解始终位于以 x e 为球心，半径为 的闭 球域S ( ) 内，即
x(t; x0 , t0 ) xe , t t0
则称系统的平衡状态 x 在李雅普诺夫意义下稳定。
e
当系统做不衰减的震荡运动
时，将描绘出一条封闭曲线 ，只要不超出 S ( ) ，则认为是 稳定的。
初始状态有界，随时间
推移，状态向量距平衡 点的距离可以维持在一 个确定的数值内，而到 达不了平衡状态。
x2
S ( )
xe
S ( )
x1
任给一个球域S ( ) ，若存在一个球域S ( ) ，使得从 S ( )出发的 轨迹不离开S ( )，则称系统的平衡状态是李雅普诺夫意义下稳定 的。 若 与初始时刻 t 0无关，则 称系统的平衡状态x e是一致
x2
S ( )
xe
S ( )
x1
近，直至到达平衡状态后
停止运动。
3、大范围渐近稳定 当初始条件扩展到整个状态空间，且平衡状态均具 有渐近稳定性时，称此平衡状态是大范围渐近稳定的。 几何意义：
李雅普诺夫稳定性分析(二)

李雅普诺夫稳定性分析(二)


但是，如果我们一时找不到这样的李雅普诺夫函 数，也并不意味着平衡态就不是渐近稳定的。 2) 对于渐近稳定的平衡态，满足条件的李雅普诺夫 函数总是存在的，但并不唯一。 3) 对于非线性系统，虽然具体的李雅普诺夫函数可 证明所讨论的系统在平衡态的邻域内是渐近稳定的， 但并不意味着在其他的区域系统是或不是渐近稳定 的; 4) 李雅普诺夫第二法的结论并没有指明寻找李雅普 诺夫函数的方法。 寻找李雅普诺夫函数的方法将依具体的系统和状 态方程而具体分析。
2 V (x) = x12 + x2 2 ′ ′ V ′(x) = 2 x1 x1 + 2 x2 x2 = −2 x2 ≤ 0
由于V’(x)是负半定函数，由定理5-5的1)可知， 系统为一致稳定的。
′ x1 = x2 ′ x2 = − x1 − x2
对例5-5，选取李雅普诺夫函数为
1 2 2 V ( x , t ) = ( x1 + x2 ) 2 + 2 x1 + x2 2
T
例5-10 控制系统方块图如下图所示。 要求系统渐近稳定，试确定增益的取值范围。
x3
k s +1
1 s+2
x2
1 s
x1
-
解: 由图可写出系统的状态方程为 ɺ 1 0 x1 x1 0 x = 0 x ɺ2 −2 1 2 x3 − k 0 − 1 x 3 ɺ
解出p11、p12和p22，得
p11 p12 1 3 1 P= = 2 1 2 p12 p22
为了验证对称矩阵P的正定性，用合同变换法 检验如下:
1 3 1 行( 2) −(1) / 3→( 2) 1 9 0 P= ⇒ 2 1 2 列( 2)−(1) / 3→( 2) 6 0 5
《现代控制理论》李雅普诺夫稳定性分析

《现代控制理论》李雅普诺夫稳定性分析

向量和矩阵的范数
1、向量空间上的欧几里德范数（即向量长度）
其欧几里德范数定义为：
一般
一、向量和矩阵的范数
预备知识
矩阵范数
矩阵 的范数定义为：
【例】
Hale Waihona Puke ， 则即:矩阵每个元素平方和开根号
预备知识
2、矩阵范数
1．二次型函数：由n个变量
组成的二次齐次多项式，称（n元）二次型函数
2．二次型函数的矩阵表示
则系统在原点处的平衡状态是不稳定的。
为唯一的平衡状态。
定理4：设系统状态方程为
李雅普诺夫主要的稳定性定理
例题
[例] 设系统状态方程为
试确定系统的稳定性。
解 xe=0
,
是该系统惟一的平衡状态。
由于当
时
,所以系统在原点处的平衡状态是
大范围渐近稳定的。
选取
李雅普诺夫主要的稳定性定理
例题
[例] 已知定常系统状态方程为
定义：若所有有界输入引起的零状态响应输出有界，则称系统为有界输入输出稳定。
李雅普诺夫第一方法—间接法
定理3：连续定常系统 传递函数为： 系统 BIBO 稳定的充要条件为：传递函数的所有极点均位于S左半平面。
【例】试分析系统渐近稳定和BIBO稳定。
李雅普诺夫主要的稳定性定理
讨论续
这是一个矛盾的结果,表明
也不是系统的
受扰运动解。综合以上分析可知,
当
时,显然有
根据定理9-12可判定系统的原点平衡状态是大范围渐近稳定的。
李雅普诺夫主要的稳定性定理
线性系统稳定性分析
一.线性定常系统李雅普诺夫稳定性分析
线性定常连续系统
系统状态方程为
李雅普诺夫稳定性基本定理

李雅普诺夫稳定性基本定理

➢ 下面我们讨论对所有动态系统的状态方程的稳 定性分析都适用的Lyapunov第二法。 Lyapunov's second method
Lyapunov第二法又称为直接法(direct method) 。 ➢ 它是在用能量观点分析稳定性的基础上建立起来的。 ✓ 若系统平衡态渐近稳定，则系统经激励后，其储存 的能量将随着时间推移而衰减。当趋于平衡态时， 其能量达到最小值。
中的坐标平移，将平衡态xe移到原点。 ➢ 因此, 上式又可转换成如下原点平衡态的线性状态方程:
x’=Ax
判别非线性系统平衡态xe稳定性的Lyapunov第一法的思想为: ➢ 通过线性化，将讨论非线性系统平衡态稳定性问题转换 到讨论线性系统 x’=Ax 的稳定性问题。
Lyapunov第一法的基本结论是:
由上述Lyapunov第一法的结论可知, 该方法与经典控制理论 中稳定性判据的思路一致, 需求解线性化状态方程或线性状 态方程的特征值, 根据特征值在复平面的分布来分析稳定性。
➢ 值得指出的区别是:
✓ 经典控制理论讨论在有界输入下的输出稳定性问题, 而Lyapunov方法讨论状态稳定性问题。
➢ 由于Lyapunov第一法需要求解线性化后系统的特征值, 因此该方法也仅能适用于非线性定常系统或线性定常系 统，但是不能推广用于时变系统。
➢ 则称函数V(x)为区域上的正定函数。Positive definite function
从定义可知，所谓正定函数，即指除零点外恒为正值的标量 函数。由正定函数的定义，相应地可定义 ➢ 负定函数 negative definite function ➢ 非负定(又称半正定或正半定)函数 non-negative definite function; positive semi-definite function ➢ 非正定函数(又称半负定或负半定) non-positive definite function; negative semi-definite function ➢ 不定函数。 indefinite function
李雅普诺夫稳定性(2)

李雅普诺夫稳定性(2)


x f (x)
的任何轨迹线的时间导数是半负定的，即
V dV (x) V x V f (x) 0 dt x x
那么称V (x) 为系统的李雅普诺夫函数。
x2
x2
V V3
V V2
V
V V1
0
V1 V2 V3 x1
x1
x(t)
x(t)
李雅普诺夫理论基础
几何解释：表示 V(x) 值的点总是指向杯底，或指向越来 越小的V (x)值等高线。
R a 1
李雅普诺夫理论基础
x1
极限环
从任何一个非零初始状态开始的系统轨线都渐近地趋近 一个极限环。这意味着如果选择稳定性定义中的 R 为足够小，使得半径为 R 的圆完全落入极限环的封 闭曲线内，那么在靠近原点处开始的系统轨线最终将 越出这个圆,因此原点是不稳定的。
李雅普诺夫理论基础
2、渐近稳定性与指数稳定性
李雅普诺夫理论基础
例：对于一阶系统 x ax bx5
原点是这个系统的两平衡点之一。这个系统在原点附近的
线性化是：
x ax
应用李雅普诺夫线性化方法，得出该非线性系统的下述稳
定性性质：
（1）a 0 渐近稳定； （2）a 0 不稳定；
（3）a 0 不能从线性化说明系统稳定性性源自。在第三种情况下，非线性系统为
征值都严格在左半复平面内），那么平衡点是渐近稳定的 （对实际的非线性系统）；
2、如果线性化后的系统是不稳定的（即如果 A的所有特征
值至少有一个严格在右半复平面内），那么平衡点是不稳 定的（对实际的非线性系统）；
3、如果线性化后的系统是临界稳定的（即如果 A 的所有特
征值都在左半复平面内，但至少有一个在 j 轴上），那 么不能从线性近似中得出任何结论（其平衡点对于非线性 系统可能是稳定的，渐近稳定的，或者是不稳定的）。

基于MATLAB的李雅普诺夫第二法稳定性分析

基于MATLAB的李雅普诺夫第二法稳定性分析引言：对于一个给定的控制系统，稳定性是系统的一个重要特性。

稳定性是系统正常工作的前提，是系统的一个动态属性。

在控制理论工程中，无论是调节器理论、观测器理论还是滤波预测、自适应理，都不可避免地要遇到系统稳定性问题，而且稳定性分析的复杂程度也在急剧增长。

当已知一个系统的传递函数或状态空间表达式时, 可以对其系统的稳定性进行分析；当系统的阶次较高时，分析、计算的工作量很大, 给系统的分析带来很大困难。

运用MATLAB 软件，其强大的科学计算能力和可视化编程功能, 为控制系统稳定性分析提供了强有力的工具。

一．MATLAB 语言简介MATLAB 是MATrix LABoratory 的缩写, 它是MA TLAB是美国MathWorks公司出品的商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境。

它具有强大的矩阵计算能力和良好的图形可视化功能, 为用户提供了非常直观和简洁的程序开发环境, 因此被称为第四代计算机语言。

MA TLAB 发展至今, 现已集成了许多工具箱, 一般来说, 它们都是由特定领域的专家开发的, 用户可以直接是用工具箱学习、应用和评估不同的方法而不需要自己编写代码，大大提高了分析运算的效率，为此MA TLAB 语言在控制工程领域已获得了广泛地应用。

二．控制系统稳定性的基本概念稳定性是控制系统的重要特性, 也是系统能够正常运行的首要条件。

如何分析系统的稳定性并提出保证系统稳定的措施, 是自动控制理论的基本任务之一。

1892年，俄国数学家李雅普诺夫（Lyaponov）提出了分析稳定性的两种方法。

第一种方法，通过对线性化系统特征方程的根的分析情况来判断稳定性，称为间接法。

此时，非线性系统必须先线性近似，而且只能使用于平衡状态附近。

第二种方法，从能量的观点对系统的稳定性进行研究，称为直接法，对线性、非线性系统都适用。

李雅普诺夫第二定理英文表示

李雅普诺夫第二定理英文表示
摘要：
1.李雅普诺夫第二定理的英文表示
2.李雅普诺夫第二定理的定义和含义
3.李雅普诺夫第二定理的应用领域
4.李雅普诺夫第二定理的重要性
正文：
李雅普诺夫第二定理是稳定性理论中的一个重要定理，它主要用于判断一个系统是否稳定。

这个定理的英文表示为"Lyapunov"s Second Theorem"。

李雅普诺夫第二定理的定义和含义是：如果一个系统的状态方程是线性的，并且存在一个正半定矩阵P，使得系统的状态方程可以写成x" = Ax + Bu 的形式，其中A、B、U 都是已知矩阵，x 是状态向量，那么这个系统就是稳定的。

这里的稳定性指的是，系统在经过任意的初始状态后，都会趋于一个稳定的状态，也就是说，系统的状态不会无限制地偏离稳定状态。

李雅普诺夫第二定理的应用领域非常广泛，它不仅可以用于线性系统的稳定性分析，还可以用于非线性系统的稳定性分析。

在工程领域，李雅普诺夫第二定理被广泛应用于控制系统的设计和分析，例如，飞机的自动驾驶系统、汽车的巡航控制系统等都离不开李雅普诺夫第二定理的应用。

李雅普诺夫第二定理的重要性在于，它为我们提供了一个判断系统稳定性的工具，可以帮助我们在设计系统时避免系统的不稳定，从而保证系统的正常运行。

李雅普诺夫第二方法判断负定

李雅普诺夫第二方法判断负定嘿，咱今儿来聊聊李雅普诺夫第二方法判断负定这事儿啊！这可真是个有点奇妙的玩意儿呢。

你想啊，就好像咱在走一条路，得判断这条路是不是稳当，能不能走得通。

李雅普诺夫第二方法就像是个厉害的导航仪，帮咱看清这条路的情况。

说起来，这负定是个啥呢？它就好像是个标志，告诉我们系统是不是稳定地朝着某个方向走。

如果是负定的，那就好像有个小箭头一直指着稳定的方向，让我们心里有底。

咱可以想象一下，一个摇摇晃晃的不倒翁，它为啥不会倒呢？就是因为它内在有某种力量在维持着平衡呀，这就有点像负定的感觉。

当系统呈现出负定时，就好像不倒翁找到了自己的平衡之道。

那怎么用李雅普诺夫第二方法去判断这个负定呢？这可得有点技巧啦！就像我们要分辨一个东西是好是坏，得从各个方面去观察、去分析。

要看看那些个数学式子啦，函数啦，是不是符合负定的特征。

这可不是随随便便就能搞定的事儿哦！得仔细琢磨，认真思考。

就好像解一道很难的谜题，得一点点地去寻找线索，去拼凑出答案。

你说，要是咱能轻松地就用这个方法判断出负定，那该多厉害呀！就像有了一双火眼金睛，能看穿一切不稳定的因素。

而且哦，这李雅普诺夫第二方法可不只是在数学里有用，在好多实际问题中也大有用处呢！比如说在工程领域，要是能判断出系统是不是稳定负定，那就能保证工程的安全和可靠啦。

想象一下，如果一座大桥在建造的时候没有考虑到稳定性，那后果得多可怕呀！但有了李雅普诺夫第二方法，就好像给大桥加上了一道保险，让我们能放心地走在上面。

总之呢，李雅普诺夫第二方法判断负定这事儿，真的是很有意思也很重要的。

我们得好好去研究它，去掌握它，让它为我们的学习和工作带来帮助呀！难道不是吗？这可真的是值得我们花时间和精力去弄明白的呀！。

非线性系统李雅普诺夫稳定性分析(2)


克拉索夫斯基法(6/7)
例4-12 试确定如下非线性系统的平衡态的稳定性:
xf(x)x13x1x2x2x23
解 由于f(x)连续可导且
f ( x ) f ( x ) ( 3 x 1 x 2 ) 2 ( x 1 x 2 x 2 3 ) 2 0
可取作李雅普诺夫函数,因此,有
J(x) fx(x)13
➢ 由克拉索夫斯基定理可知,系统的平衡态xe=0是渐近稳定 的条件是J(x)+J(x)为负定矩阵函数。
✓ 由负定矩阵的性质知,此时雅可比矩阵J(x)的对角线 元素恒取负值,因此向量函数f(x)的第i个分量必须包 含变量xi,否则,就不能应用克拉索夫斯基定理判别该 系统的渐近稳定性。
➢ 将克拉索夫斯基定理推广到线性定常连续系统可知:对称 矩阵A+A负定,则系统的原点是大范围渐近稳定的。
fi
(0)
ki,1
fi
0 (xi xi
)
ki,2
xi 0
fi( x i)
k i,2 x i fi( x i) k i,1 x i
xi
图5-8 一类静态非线性特性
➢ 上述非线性函数fi(xi)为通过坐标原点,且介于直线ki,1xi和 ki,2xi之间的任意形状的曲线函数,因此具有一定的代表性, 可用来描述一大类非线性系统。
x14
a12 2
x
1
1
a22
x
a12
➢ 由于0<a12<a22,故V(x)是正定的。 ✓ 因此,该系统原点是渐近稳定的。
✓ 当||x||→∞时,有V(x)→∞,所以该系统原点是系统大范 围渐近稳定的。
阿依捷尔曼法(1/10)
5.4.3 阿依捷尔曼法

李亚普诺夫判稳第二法 现代控制理论 教学PPT课件


假设 V ( x) 0
V ( x) 2(1 x2 )2 x22
a.x2 (t) 0, x1任意
x2
(t )
0
x2
x2
(t ) (t )
0 0
x1 (t )
x1
(t
)
0 0
意味只有零平衡状态才满足。
b.x2 (t) 1, x1任意
x2
(t
)
1
x2 x2
(t (t
) )
1 0
由判据3，系统在零平衡状态是不稳定的。
2021年4月30日
第5章第19页
例5.18 分析此系统的稳定性。
解1）求平衡状态
xe1 xe2
0 0
2）选择能量函数
0 x 1
1 1 x
a.V ( x) 2x12 x22 0 V ( x) 4x1x1 2x2x2 4x1(x2 ) 2x2 (x1 x2 ) 2x1x2 2x22,不定
2021年4月30日
第5章第18页
例5.16分析系统的稳定性。
x
Ax,
A
1 1
1 1
解1）求平衡状态
2）选择能量函数
xe1
xe
2
0 0
V ( x) x12 x22 0 V ( x) 2x1x1 2x2 x2 2x1(x1 x2 ) 2x2 (x1 x2 ) 2(x12 x22 ) 0
x1 (t )
R L
x1 (t )
1 L
x2 (t)
iR L
x2 (t)
1 C
x1 (t )
u
Cy
y(t) x2 (t)
电容能量 电感能量
T
Q2 2C
1 2

李雅普诺夫第二法

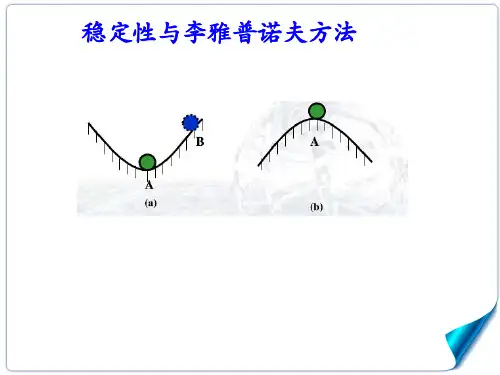
李雅普诺夫第二法李雅普诺夫第二法又称直接法，它是从能量观点进行稳定性分析的，它的基本思想是建立在这样一个物理事实基础之上，即：由经典力学理论可知，对于一个振动系统，如果系统的总能量随时间增长而连续减少，直到平衡状态为止，那么振动系统是稳定的。

1）渐进稳定的判据定理1设系统的状态方程为(,)x f x t =其中平衡状态为0e x =，满足(0,)0f t =，如果存在一个具有连续一阶偏导数的标量函数(,)v x t ，且满足以下条件：（1）(,)v x t 是正定的；（2）(,)vx t 是负定的。

则系统在原点处的平衡状态是一致渐进稳定的。

此外，如果当||||x →∞,有(,)v x t →∞，则在原点处的平衡状态是大范围一致渐进稳定的。

2）渐进稳定的判据定理1设系统的状态方程为(,)x f x t =其中平衡状态为(0,)0f t =，如果存在一个具有连续一阶偏导数的标量函数(,)v x t ，且满足以下条件：（1）(,)v x t 是正定的；（2）(,)vx t 是负定的。

（3）(,)v x t 在0x ≠时不恒等于零，则系统在原点处的平衡状态是大范围渐进稳定的。

3）李雅普诺夫意义下稳定的判别定理设系统的状态方程为=x f x t(,)其中平衡状态为(0,)0f t=，如果存在一个具有连续一阶偏导数的标量函数v x t，且满足以下条件：(,)（1）(,)v x t是正定的；（2）(,)是负定的。

v x t（3）则系统在原点处的平衡状态在李雅普诺夫意义下是一致稳定的。

4）不稳定的判别定理设系统的状态方程为=x f x t(,)其中平衡状态为(0,)0f t=，如果存在一个具有连续一阶偏导数的标量函数v x t，且满足以下条件：(,)（1）(,)v x t是正定的；（2）(,)是正定的。

v x t则系统在原点处的平衡状态是不稳定。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。


上式为向量函数的雅可比矩阵。
f f1
令
f2 fn
T
x x1 x2 xn
T
x x f ( xe )
f A T x
x xe
x x xe
则线性化系统方程为：
x Ax
结论： 1) 若 Re(i ) 0 i 1,2,, n ，则非线 性系统在 xe 处是渐进稳定的，与 g ( x) 无关。 2) 若 Re(i ) 0 Re( j ) 0 i j 1,, n 则不稳定。 3) 若 Re(i ) 0，稳定性与 g ( x)有关，
f x f ( xe ) T x
其中：
( x xe ) g ( x)
x xe
g ( x) --级数展开式中二阶以上各项之和)
f1 x f 1 T x f n x1 f1 x2 f n x2 f1 xn f n xn
g ( x) 0 则是李雅普诺夫意义下的稳定性。
5.4 李雅普诺夫第二法(直接法)
稳定性定理：
f ( x, t ) 设系统状态方程：x 其平衡状态满足 f (0, t ) 0 ，假定 状态空间原点作为平衡状态( xe 0)，并设 在原点领域存在 V ( x, t )对 x 的连续的一阶 偏导数。
A非奇异： A奇异：
Axe 0 xe 0 Axe 0 有无穷多个 xe
b.非线性系统
f ( xe , t ) 0 可能有多个 xe x
eg. x 1 x1
2 x1 x2 x x
令
3 2
1 0 x
xe 1 0

5.3 李雅普诺夫第一法（间接法） 利用状态方程解的特性来判断系统稳定性。 1. 线性定常系统稳定性的特征值判据：
Ax x(0) x0 t 0 x
1）李氏稳定的充要条件：
Re(i ) 0
i 1,2, n
即系统矩阵A的全部特征值位于复平面左半 部。
Байду номын сангаас
2.
非线性系统的稳定性分析： 假定非线性系统在平衡状态附近可展 开成台劳级数，可用线性化系统的特征值 判据判断非线性系统的平衡状态处的稳定 性。 设非线性系统状态方程： f ( x) f ( x) --非线性函数 x 在平衡状态 xe 0附近存在各阶偏导 数，于是：
如果对每个实数 0 都对应存在另 一个实数 ( , t0 ) 0 满足
x0 xe ( , t0 )
的任意初始态 x0 出发的运动轨迹
x(t; x0 , t0 )，在t 都满足：
x(t; x0 , t0 ) xe , t t0
则称 xe 是李雅普诺夫意义下稳定的。

当 与 t 0 无关 大范围一致渐近稳定。 必要条件：在整个状态空间中只有一个平 衡状态xe
有多小，只要 s( ) 4. 不稳定性：不管 ， 内由 x0 出发的轨迹超出 s( )以外，则称此 平衡状态是不稳定的。
线性系统的平衡状态不稳定 表征系统不稳定。 非线性系统的平衡状态不稳定 只说明存在局 发散的轨迹。至于是否趋 于无穷远 域外是否存在其它平衡状态。 s( ) 若存在极限环，则系统仍是李雅普诺夫意义下 的稳定性。
t

都有 lim x(t; x0 , t0 ) xe 0
初始条件扩展到整个空间，且是渐近稳定性。
s( ) ,
x xe大范围稳定
线性系统(严格)：如果它是渐近稳定的，必
是有大范围渐近稳定性(线性系统稳定性与初
始条件的大小无关)。 非线性系统：只能在小范围一致稳定，由状 态空间出发的轨迹都收敛 xe 或其附近。
定理1：若(1) V ( x, t ) 正定； . (2) V ( x, t ) 负定； 则原点是渐近稳定的。 . 说明： V ( x, t ) 负定 能量随时间连续单调 衰减。 定理2：若(1) V . ( x, t ) 正定； (2) V . ( x, t ) 负半定； (3) V [ x(t ; x0 , t ), t ] 在非零状态不 恒为零，则原点是渐近稳定的。
2 0 x
0 xe3 1

0 xe2 1
0
4.
孤立的平衡状态：在某一平衡状态的充分 小的邻域内不存在别的平衡状态。 对于孤立的平衡状态，总可以经过适当的 坐标变换，把它变换到状态空间的原点。
5.2 李雅普诺夫意义下的稳定 1.李氏意义下的稳定
奈魁斯特判据，对数判据，根轨迹判据 非线性系统：相平面法(适用于一，二阶非 线性系统)
1982年，俄国学者李雅普诺夫提出的稳定
性定理采用了状态向量来描述，适用于单 变量，线性，非线性，定常，时变，多变 量等系统。 应用：自适应，最优控制，非线性控制等。
主要内容： 李氏第一法（间接法）：求解特征方程 的特征值 李氏第二法（直接法）：利用经验和技巧 来构造李氏函数
与 t 0 有关 时变：
定常系统： 与t 0无关，xe 是一致稳定的。 注意： －向量范数(表示空间距离) 欧几里得范数。
2.渐近稳定 1）是李氏意义下的稳定
x(t ; x0 , t0 ) xe 0 2）lim t
与t0无关 一致渐近稳定
3.大范围内渐近稳定性
对 x0 s( )
研究的目的和意义:稳定性是自动控制系统
正常工作的必要条件，是一个重要特征。 要求：在受到外界扰动后，虽然其原平衡 状态被打破，但在扰动消失后，仍然能恢 复到原来的平衡状态，或者趋于另一平衡 状态继续工作。 稳定性：系统在受到小的外界扰动后，系 统状态方程解的收敛性，而与输入作用无 关。
经典控制理论稳定性判别方法：代数判据，
5.1 稳定性基本概念
1.自治系统：输入为0的系统 x =Ax+Bu(u=0)
=f(x,t)的解为 x(t; x0 , t0 ) 2.初态 x
x(t0 , x0 , t0 ) x0 初态
3.平衡状态：

xe 系统的平衡状态 e f ( xe , t ) 0 x n Ax a.线性系统 xR x