平面的基本性质(2)
- 格式:ppt
- 大小:2.00 MB
- 文档页数:2






高中数学的必修二数学平面的基本性质知识点平面的基本性质教学目标1、知识与能力:(1)巩固平面的基本性质即四条推断出公理和三条推论.(2)能使用公理和推论进行解题.2、过程与方法:(1)体验在空间确定一个平面的过程与方法;(2)掌握利用平面的基本性质证明三点共线、三线共点、多线共面的方法。
3、情感成见与价值观:培养学生认真观察的态度,慎密思考的习惯,提高学生审美能力和空间想象的能力。
教学重点平面的三条基本性质即三条推论.教学难点准确运用三条公理和推论解题.教学过程一、问题情境问题1:空间共点的三条直线二维能确定几个平面?空间互相对角线平行的三条直线呢?问题2:如何判断办公桌的四条腿内则的底端是否在一个平面内?二、温故知新公理1一处如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.公理2如果两个平面有两个一个公共设施点,那么它们还有其它公用点,这些公共点的集合是经过这个公共给定点的一条直线.公理3经过不在同一条直线上的三点,有且只有一个平面.推论1经过一条直线和这条直线外的一点,有且只有一个平面.推论2经过两条直角直线,有且只有一个平面.推论3经过两条平行平行线,有且只有一个平面.公理4(平行公理)平行于同一条直线的两条直线互相平行.把作出以上各公理及推论进行对比:三、数学运用基础训练:(1)已知:;求证:直线AD、BD、CD共面.证明:——公理3推论1——公理1同理可证,,直线AD、BD、CD共面【解题反思1】1。
逻辑要严谨2.书写要规范3.证明共面的步骤:(1)确定平面——公理3及其3个推论(2)证线“归”面(线在面内如:)——公理1(3)作出结论。
变式1、如果直线两两交汇,那么这三条直线是否共面?(口答)变式2、已知空间不共面的二点,过其中任意三点可以三维空间确定一个平面,由这四个一两个点能确知几个平面?变式3、四条线段顺次首尾连接,所得的图形一定是平面曲面图形吗?(口答)(2)已知直线满足:;求证:直线证明:——公理3推论3——公理1直线共面提高训练:已知,求证:四条直线在同一平面内.思路分析:考虑由直线a,b确定一个平面,再证明直线c,l在此平面上,但十分困难。




0441.平面的基本性质与推论(2)课型:新授课编制人:年级主任:班级:姓名:编号:0441.2.1 平面的基本性质与推论(2)一、学习目的1、会判别空间两直线的位置关系.2、了解两异面直线的定义,会求两异面直线所成的角.3、能用公理4处置一些复杂的相关效果.二、基础知识1、空间两条直线的位置关系有且只要三种:______________、________________、________________.2、异面直线的定义:________________________________的两条直线叫做异面直线.3、公理4:平行于同一条直线的两条直线____________.4、等角定理:空间中假设两个角的两边区分对应________,那么这两个角________或________.5、异面直线所成的角:直线a,b是异面直线,经过空间任一点O,作直线a′,b′,使________,________,我们把a′与b′所成的______________叫做异面直线a与b所成的角(或夹角).假设两条直线所成的角是________,那么我们就说这两条异面直线相互垂直,两条异面直线所成的角的取值范围是________.三、基础自测:1、区分在两个相交平面内的两条直线间的位置关系是( )A.异面 B.平行 C.相交 D.以上都有能够2、假定a和b是异面直线,b和c是异面直线,那么a和c的位置关系是( )A.异面或平行 B.异面或相交 C.异面 D.相交、平行或异面3、以下四个结论中假命题的个数是( )①垂直于同不时线的两条直线相互平行;②平行于同不时线的两直线平行;③假定直线a,b,c满足a∥b,b⊥c,那么a⊥c;④假定直线l1,l2是异面直线,那么与l1,l2都相交的两条直线是异面直线.A.1 B.2 C.3 D.44、如图,长方体ABCD—A′B′C′D′中,AB=23,AD=23,AA′=2.(1)BC和A′C′所成的角是多少度?(2)AA′和BC′所成的角是多少度?四、典型例题:例1、如下图,空间四边形ABCD中,E、F、G、H区分是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.假定在例1中,假设再加上条件AC=BD,那么四边形EFGH是例2 如右图,正方体ABCD—A′B′C′D′.(1)哪些棱所在直线与直线BA′是异面直线?(2)直线BA′和CC′的夹角是多少?例3、如图,在三棱锥A-BCD中,E,F,G区分是AB,BC,AD的中点,∠GEF=120°,那么BD和AC所成角的度数为________.例4、如下图,正方体AC1中,E、F区分是A1B1、B1C1的中点,求异面直线DB1与EF所成角的大小.五、课堂练习1、如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.(1)求四棱锥O-ABCD的体积;(2)求异面直线OC与MD所成角的正切值的大小.2、空间四边形ABCD中,AB=CD且AB与CD所成的角为30°,E、F区分是BC、AD的中点,求EF与AB所成角的大小.【当堂检测】1、正方体ABCD—A′B′C′D′中:(1)BC′与CD′所成的角为________;(2)AD与BC′所成的角为________.2、一个正方体纸盒展开后如下图,在原正方体纸盒中有如下结论:①AB⊥EF;②AB与CM所成的角为60°;③EF与MN是异面直线;④MN∥CD.以上结论中正确结论的序号为________.。
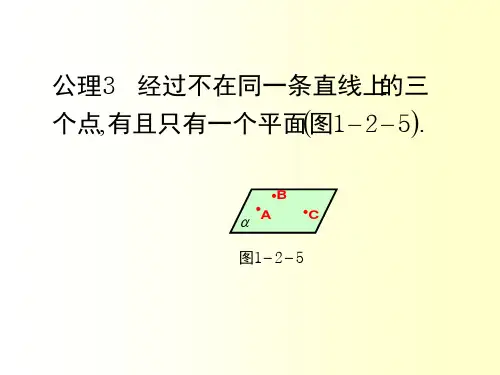
1.2.1平面的基本性质及推论(二)教学目标:理解推论1、2、3的内容及应用教学重点:理解推论1、2、3的内容及应用教学过程:推论1:直线及其外一点确定一个平面(一) 推论2:两相交直线确定一个平面(二) 推论3:两平行直线确定一个平面(四)例1已知:空间四点A 、B 、C 、D 不在同一平面内.求证:AB 和CD 既不平行也不相交.证明:假设AB 和CD 平行或相交,则AB 和CD 可确定一个平面α,则α⊂AB ,α⊂CD ,故α∈A ,α∈B , α∈C ,α∈D .这与已知条件矛盾.所以假设不成立,即AB 和CD 既不平行也不相交.卡片:1、反证法的基本步骤:假设、归谬、结论;2、归谬的方式:与已知条件矛盾、与定理或公理矛盾、自相矛盾.例2已知:平面α⋂平面β=a ,平面α⋂平面γ=b ,平面γ⋂平面β=c 且c b a 、、不重合.求证:c b a 、、交于一点或两两平行.证明:(1)若三直线中有两条相交,不妨设a 、b 交于A .因为,β⊂a ,故β∈A ,同理,γ∈A ,故c A ∈.所以c b a 、、交于一点.(2)若三条直线没有两条相交的情况,则这三条直线两两平行.综上所述,命题得证.例3已知ABC ∆在平面α外,它的三边所在的直线分别交平面α于R Q P 、、.求证:R Q P 、、三点共线. 证明:设ABC ∆所在的平面为β,则R Q P 、、为平面α与平面β的公共点,所以R Q P 、、三点共线.卡片:在立体几何中证明点共线,线共点等问题时经常要用到公理2.例4正方体1111D C B A ABCD -中,E 、F 、G 、H 、K 、L 分别是、、、111D A DD DC BC BB B A 、、111的中点.求证:这六点共面. 证明:连结BD 和KF , 因为 L E 、是CB CD 、的中点,所以 BD EL //. 又 矩形11B BDD 中BD KF //,所以 EL KF //,所以 EL KF 、可确定平面α,所以 L K F E 、、、共面α,同理 KL EH //, A B C PQ R αC A A B B C D DEF G H K L 1111故 L K H E 、、、共面β.又 平面α与平面β都经过不共线的三点L K E 、、,故 平面α与平面β重合,所以E 、F 、G 、H 、K 、L 共面于平面α.同理可证α∈G ,所以,E 、F 、G 、H 、K 、L 六点共面.卡片:证明共面问题常有如下两个方法:(1)接法:先确定一个平面,再证明其余元素均在这个平面上;(2)间接法:先证明这些元素分别在几个平面上,再证明这些平面重合.课堂练习:1.判断下列命题是否正确(1)如果一条直线与两条直线都相交,那么这三条直线确定一个平面. ( )(2)经过一点的两条直线确定一个平面. ( )(3)经过一点的三条直线确定一个平面. ( )(4)平面α和平面β交于不共线的三点A 、B 、C . ( )(5)矩形是平面图形. ( )2.空间中的四点,无三点共线是四点共面的 条件.3.空间四个平面两两相交,其交线条数为 .4.空间四个平面把空间最多分为 部分.5.空间五个点最多可确定 个平面.6.命题“平面α、β相交于经过点M 的直线a ”可用符号语言表述为 .7.梯形ABCD 中,AB ∥CD ,直线AB 、BC 、CD 、DA 分别与平面α交于点E 、G 、F 、H .那么一定有G 直线EF ,H 直线EF .8.求证:三条两两相交且不共点的直线必共面.小结:本节课学习了平面的基本性质的推论及其应用课后作业:略。