下载文档原格式
高等数学(下)教案曲面及其方程教学目标：1. 理解曲面的概念，掌握曲面的基本性质。
2. 学习曲面的方程表示方法，掌握常见曲面的方程。
3. 能够利用曲面方程进行曲面的绘制和分析。
教学内容：一、曲面的概念与基本性质1. 曲面的定义2. 曲面的基本性质2.1 曲面的导数2.2 曲面的切线和法线2.3 曲面的曲率2.4 曲面的切平面和法平面二、曲面的方程表示方法1. 参数方程表示法2.1 参数方程的定义2.2 参数方程的求导和积分2. 普通方程表示法2.1 普通方程的定义2.2 普通方程的求导和积分3. 柱面和二次曲面的方程3.1 柱面的方程3.2 二次曲面的方程三、常见曲面的方程1. 圆锥面的方程2. 椭圆面的方程3. 双曲面的方程4. 抛物面的方程5. 直纹面的方程四、曲面的绘制和分析1. 利用参数方程绘制曲面2. 利用普通方程绘制曲面3. 曲面的切线和法线分析4. 曲面的曲率分析5. 曲面的切平面和法平面分析教学方法：1. 采用多媒体教学，通过图形和动画展示曲面的形状和性质。
2. 通过例题讲解和练习，使学生掌握曲面方程的求解和分析方法。
3. 引导学生运用曲面方程解决实际问题，提高学生的应用能力。
教学评价：1. 课堂讲解和练习的参与度。
2. 学生对曲面方程的掌握程度。
3. 学生能够运用曲面方程进行曲面的绘制和分析。
教学资源：1. 教学PPT和动画演示。
2. 曲面方程的相关教材和参考书。
3. 计算机软件进行曲面的绘制和分析。
六、曲面的切平面和法线1. 切平面的定义与性质6.1 切平面的定义6.2 切平面的性质2. 法线的定义与性质6.3 法线的定义6.4 法线的性质3. 切平面和法线的求法6.5 切平面和法线的求法七、曲面的曲率1. 曲率的定义与性质7.1 曲率的定义7.2 曲率的性质2. 曲率的计算7.3 曲率的计算方法3. 曲面的弯曲程度分析7.4 曲面的弯曲程度分析八、曲面的绘制与分析实例1. 实例一：圆锥面的绘制与分析8.1 圆锥面的参数方程8.2 圆锥面的普通方程8.3 圆锥面的切平面和法线分析2. 实例二：椭圆面的绘制与分析8.4 椭圆面的参数方程8.5 椭圆面的普通方程8.6 椭圆面的切平面和法线分析3. 实例三：双曲面的绘制与分析8.7 双曲面的参数方程8.8 双曲面的普通方程8.9 双曲面的切平面和法线分析九、曲面在实际问题中的应用1. 曲面在工程中的应用9.1 曲面在机械设计中的应用9.2 曲面在建筑设计中的应用2. 曲面在自然科学中的应用9.3 曲面在光学中的应用9.4 曲面在声学中的应用十、复习与练习1. 复习本章内容10.1 复习曲面的概念与基本性质10.2 复习曲面的方程表示方法10.3 复习常见曲面的方程2. 课堂练习10.4 完成课堂练习题3. 课后作业10.5 布置课后作业教学方法：1. 采用案例教学法，通过具体实例讲解曲面的绘制与分析方法。
课题：10.1平面的基本性质课题：10.1平面的基本性质【教学目标】1.知识目标：理解和掌握平面的三个基本性质，并学会应用性质进行一些简单的分析和判断。
2. 能力目标：通过实例和多媒体进行直观教学，培养学生的观察能力和空间想象能力。
通过应用性质进行一些简单的分析和判断，培养逻辑思维能力。
3.情感目标：（1）通过创设主题式故事情境，增强学习兴趣。
（2）结合生活，进行“数学来源于生活”的唯物主义观念教育。
（3）通过问题解决，培养学生合作交流、独立思考等良好的个性品质，以及勇于批判、敢于创新的科学精神。
【教学重点】平面的基本性质。
因为研究空间图形时，往往将有关点、线归结到一个平面内，再利用平面图形的性质解决。
所以要求学生对基本性质有较深刻的理解。
【教学难点】平面的基本性质的掌握与运用。
因为平面的基本性质既抽象又枯燥，而中职幼师专业的学生想象和思维都较弱，所以掌握与运用三个平面的基本性质会有一定的难度。
【教学方法】遵循学生的认知规律，结合多媒体将具体与抽象、感性与理性、动手与动脑有机地结合在一起。
进行思考、交流，师生共同讨论等学法。
根据中职学生想象能力、思维能力较弱的特点，尽量从直观入手，因此考虑通过创设既靠近生活，又体现数学本质，并且能从情感上激发学生主动、深入思考的有效情境（主题式故事情境）作为载体的启发式教法。
【教学过程】图9−5公理1作为判断和证明直线是否在平图9−8反映了只要“两面共一点”，就两面共一线，且过这一点，线唯把信封的一角竖立在桌面上，那么信封所在平面和桌面所在平面只交于一点，对吗？如图：在长方体ABCD—A1B1C1D1是棱A1B1上的中点，画出C1三点所确定的平面α与长方体表面的交线。
数学1第1章集合1.1集合的含义及其表示1.2子集、全集、补集1.3交集、并集第2章函数概念与基本初等函数Ⅰ2.1函数的概念和图象函数的概念和图象函数的表示方法函数的简单性质映射的概念2.2指数函数分数指数幂指数函数2.3对数函数对数对数函数2.4幂函数2.5函数与方程二次函数与一元二次方程用二分法求方程的近似解2.6函数模型及其应用数学2第3章立体几何初步3.1空间几何体棱柱、棱锥和棱台圆柱、圆锥、圆台和球中心投影和平行投影直观图画法空间图形的展开图柱、锥、台、球的体积3.2点、线、面之间的位置关系平面的基本性质空间两条直线的位置关系直线与平面的位置关系平面与平面的位置关系第4章平面解析几何初步4.1直线与方程直线的斜率直线的方程两条直线的平行与垂直两条直线的交点平面上两点间的距离点到直线的距离4.2圆与方程圆的方程直线与圆的位置关系圆与圆的位置关系4.3空间直角坐标系空间直角坐标系空间两点间的距离数学3第5章算法初步5.1算法的意义5.2流程图5.3基本算法语句5.4算法案例第6章统计6.1抽样方法6.2总体分布的估计6.3总体特征数的估计6.4线性回归方程第7章概率7.1随机事件及其概率7.2古典概型7.3几何概型7.4互斥事件及其发生的概率数学4第8章三角函数8.1任意角、弧度8.2任意角的三角函数8.3三角函数的图象和性质第9章平面向量9.1向量的概念及表示9.2向量的线性运算9.3向量的坐标表示9.4向量的数量积9.5向量的应用第10章三角恒等变换10.1两角和与差的三角函数10.2二倍角的三角函数10.3几个三角恒等式数学5第11章解三角形11．1正弦定理11．2余弦定理11．3正弦定理、余弦定理的应用第12章数列12．1等差数列12．2等比数列12．3数列的进一步认识第13章不等式13．1不等关系13．2一元二次不等式13．3二元一次不等式组与简单的线性规划问题13．4基本不等式选修系列11-1第1章常用逻辑用语1．1命题及其关系1．2简单的逻辑联结词1．3全称量词与存在量词第2章圆锥曲线与方程2．1圆锥曲线2．2椭圆2．3双曲线2．4抛物线2．5圆锥曲线与方程第3章导数及其应用3．1导数的概念3．2导数的运算3．3导数在研究函数中的应用3．4导数在实际生活中的应用1-2第1章统计案例1．1假设检验1．2独立性检验1．4聚类分析第2章推理与证明2．1合情推理与演绎推理2．2直接证明与间接证明2．3公理化思想第3章数系的扩充与复数的引入3．1数系的扩充3．2复数的四则运算3．3复数的几何意义第4章框图4．1流程图5．2结构图选修系列22-1第1章常用逻辑用语1．1命题及其关系1．2简单的逻辑连接词1．3全称量词与存在量词第2章圆锥曲线与方程2．1圆锥曲线2．2椭圆2．3双曲线2．4抛物线2．5圆锥曲线的统一定义2．6曲线与方程第3章空间向量与立体几何3．1空间向量及其运算3．2空间向量的应用2-2第1章导数及其应用1．1导数的概念1．2导数的运算1．3导数在研究函数中的应用1．4导数在实际生活中的应用1．5定积分第2章推理与证明2．1合情推理与演绎推理2．2直接证明与间接证明2．4公理化思想第3章数系的扩充与复数的引入6．1数系的扩充3．2复数的四则运算3．3复数的几何意义2-3第1章计数原理1．1两个基本原理1．2排列1．3组合1．4计数应用题1．5二项式定理第2章概率2．1随机变量及其概率分布2．2超几何分布2．3独立性2．4二项分布2．5离散型随机变量的均值与方差2．6正态分布第3章统计案例3．1假设检验3．2独立性检验3．3线性回归分析4．4聚类分析。
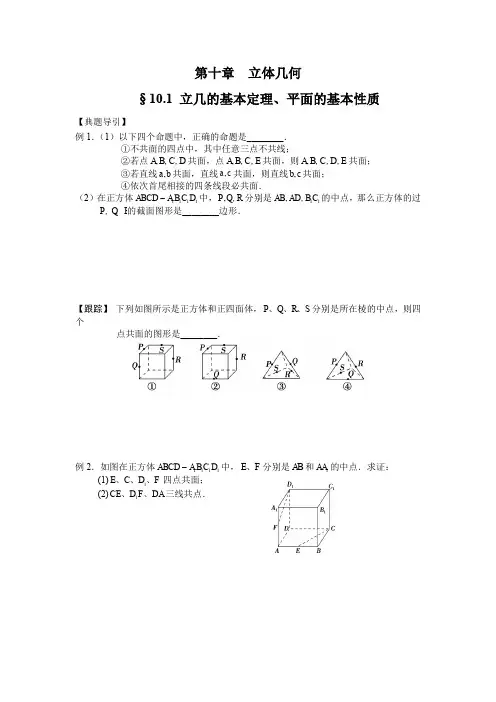
第十章 立体几何§10.1 立几的基本定理、平面的基本性质【典题导引】例1．（1）以下四个命题中，正确的命题是________．①不共面的四点中，其中任意三点不共线；②若点,A B C D ,,共面，点,A B C E ,,共面，则,A B C D E ,,,共面； ③若直线,a b 共面，直线,a c 共面，则直线,b c 共面； ④依次首尾相接的四条线段必共面．（2）在正方体1111ABCD A B C D -中，,P Q R ,分别是11,AB AD B C ,的中点，那么正方体的过 P Q R ,,的截面图形是________边形．【跟踪】 下列如图所示是正方体和正四面体，P Q R S 、、、分别是所在棱的中点，则四个点共面的图形是________．例2．如图在正方体1111ABCD A B C D -中，E F 、分别是AB 和1AA 的中点．求证：(1)1E C D F 、、、四点共面； (2)1CE D F DA 、、三线共点．例3．在正方体1111ABCD A B C D -中，对角线1A C 与平面1BDC 交于点O ，AC BD ,交于点M ，求证：点1,C O M ,共线．例4．如图，正方体1111ABCD A B C D -中，E 为棱1DD 的中点． （1）求证：1//BD 平面ACE ；（2）求证：平面ACE ⊥平面11BB D ．ABCD 1A 1B 1C 1DE【课后巩固】1．在平行六面体1111ABCD A B C D -中，既与AB 共面又与1CC 共面的棱的条数为________．2．给出以下命题：①和一条直线都相交的两条直线在同一平面内；②三条两两相交的直线在同一平面内；③有三个不同公共点的两个平面重合；④两两平行的三条直线确定三个平面．其中正确命题的个数是________．3．123,l l l ,是空间三条不同的直线，给出下列四个命题： ①122313,//l l l l l l ⊥⊥⇒； ②122313,//l l l l l l ⊥⇒⊥；③123123////l l l l l l ⇒,,共面； ④123,l l l ,共点123,l l l ⇒,共面． 其中正确命题的序号是________．4．在正方体1111ABCD A B C D -中，,E F 分别是棱1111,A B A D 的中点，则1A B 与EF 所成角的大小为________．5．如果两条异面直线称为“一对”，那么在正方体的十二条棱中共有异面直线________对．6．如图，在正方体1111ABCD A B C D -中，,M N 分别为棱111,C D C C 的中点，有以下四个结论：①直线AM 与1CC 是相交直线；②直线AM 与BN 是平行直线； ③直线BN 与1MB 是异面直线； ④直线AM 与1DD 是异面直线． 其中正确的结论为________(注：把你认为正确的结论的序号都填上)．7．对于不同的直线,m n 和不同的平面,,αβγ，有如下四个命题： ①若//m α，m n ⊥，则n α⊥； ②若m α⊥，m n ⊥，则//n α； ③若αβ⊥，γβ⊥，则//αγ；④若m α⊥，//m n ，n β⊂，则αβ⊥． 其中是真命题的是________．8．在正方体1111ABCD A B C D -中，,E F 分别为棱11,AA CC 的中点，则在空间中与三条直线11,,A D EF CD 都相交的直线有________条．9．如图，四边形ABEF 和ABCD 都是直角梯形，90BAD FAB ∠=∠=︒，12BC AD =且//BC AD ，12BE FA =且//BE FA ，,G H 分别为FA FD ,的中点．(1)证明：四边形BCHG 是平行四边形；(2),C D F E ,,四点是否共面？为什么？10．如图，正方体1111ABCD A B C D -中，E 为棱1DD 的中点． （1）求证：1//BD 平面ACE ；（2）求证：平面ACE ⊥平面11BB D ．11．如图，在直四棱柱ABCD ﹣A 1B 1C 1D 1中， E ，F 分别是AB ，BC 的中点，A 1C 1 与B 1D 1交于点O .（1）求证：A 1，C 1，F ，E 四点共面；（2）若底面ABCD 是菱形，且OD ⊥A 1E ，求证：OD ⊥平面A 1C 1FE .（第11图）1EABA B C D 1A 1B 1C 1D E。
10.1平面及其基本性质（4）——课后作业
1．画水平放置的边长为6cm的正方形的直观图．
2、用斜二测画法画长、宽、高分别为8、6、4的长方体的直观图．
3、在水平放置的平面上有一个边长为3cm的正三角形，请画出其直观图.
4、画出如图水平放置的直角梯形OABC的直观图
5．如图，若平行四边形''''A B C D 是用斜二测画法画出的水平放置的平面图形ABCD 的直观图．已知''4A B =cm ，'''45D A B ∠=︒，平行四边形''''A B C D 的面积为28cm ，则原平面图形ABCD 中AD 的长度为__________．
6．设△ABC 是水平放置的等边三角形．以其底边BC 所在直线为x 轴，底边BC 上的高所在直线为y 轴，建立平面直角坐标系，并用斜二测画法画出它的直观图，则原三角形的面积与其直观图的面积之比为________．
巩固题
7．判断下列命题的真假：
（1）一条直线和一个点确定一个平面；（ ）
（2）若点A 、B 在圆O 上，则A 、B 、O 可以确定一个平面；（ ）
（3）如果两个平面至少有三个公共点，那么这两个平面重合．（ ）
8．求证：三角形是一个平面图形（即三角形的三边在同一个平面上）．
9．已知空间中三条直线a 、b 、c 两两平行，那么这三条直线共面吗？如果直线a 、b 、c 两两平行，直线d 与直线a 、b 、c 都相交，那么直线a 、b 、c 共面吗？请说明理由．。
高中数学目录江苏高中数学教材目录苏教版高中数学有: 《必修一》、《必修二》、《必修三》、《必修四》、《必修五》【文理兼学】《选修1,1》【文科】、《选修1,2》【文科】第1章集合1.1集合的含义及其表示 1.2子集、全集、补集 1.3交集、并集第2章函数概念与基本初等函数?2.1函数的概念和图象函数的概念和图象函数的表示方法函数的简单性质映射的概念2.2指数函数分数指数幂指数函数2.3对数函数对数对数函数2.4幂函数2.5函数与方程二次函数与一元二次方程用二分法求方程的近似解 2.6函数模型及其应用数学2第3章立体几何初步 3.1空间几何体棱柱、棱锥和棱台圆柱、圆锥、圆台和球中心投影和平行投影直观图画法空间图形的展开图柱、锥、台、球的体积 3.2点、线、面之间的位置关系平面的基本性质空间两条直线的位置关系直线与平面的位置关系平面与平面的位置关系第4章平面解析几何初步4.1直线与方程直线的斜率直线的方程两条直线的平行与垂直两条直线的交点平面上两点间的距离点到直线的距离4.2圆与方程圆的方程直线与圆的位置关系圆与圆的位置关系 4.3空间直角坐标系空间直角坐标系空间两点间的距离数学3第5章算法初步 5.1算法的意义5.2流程图5.3基本算法语句 5.4算法案例第6章统计6.1抽样方法6.2总体分布的估计 6.3总体特征数的估计 6.4线性回归方程第7章概率7.1随机事件及其概率 7.2古典概型7.3几何概型7.4互斥事件及其发生的概率数学4第8章三角函数8.1任意角、弧度8.2任意角的三角函数 8.3三角函数的图象和性质第9章平面向量9.1向量的概念及表示 9.2向量的线性运算 9.3向量的坐标表示 9.4向量的数量积9.5向量的应用第10章三角恒等变换 10.1两角和与差的三角函数 10.2二倍角的三角函数10.3几个三角恒等式数学5第11章解三角形11(1正弦定理11(2余弦定理11(3正弦定理、余弦定理的应用第12章数列12(1等差数列12(2等比数列12(3数列的进一步认识第13章不等式13(1不等关系13(2一元二次不等式 13(3二元一次不等式组与简单的线性规划问题13(4基本不等式选修系列11-1第1章常用逻辑用语 1(1命题及其关系 1(2简单的逻辑联结词 1(3全称量词与存在量词第2章圆锥曲线与方程 2(1圆锥曲线2(2椭圆2(3双曲线2(4抛物线2(5圆锥曲线与方程第3章导数及其应用 3(1导数的概念3(2导数的运算3(3导数在研究函数中的应用3(4导数在实际生活中的应用1-2第1章统计案例1(1假设检验1(2独立性检验1(3线性回归分析 1(4聚类分析第2章推理与证明 2(1合情推理与演绎推理 2(2直接证明与间接证明 2(3公理化思想第3章数系的扩充与复数的引入3(1数系的扩充3(2复数的四则运算 3(3复数的几何意义第4章框图4(1流程图5(2结构图选修系列22-1第1章常用逻辑用语 1(1命题及其关系 1(2简单的逻辑连接词1(3全称量词与存在量词第2章圆锥曲线与方程 2(1圆锥曲线2(2椭圆2(3双曲线2(4抛物线2(5圆锥曲线的统一定义 2(6曲线与方程第3章空间向量与立体几何 3(1空间向量及其运算 3(2空间向量的应用 2-2 第1章导数及其应用 1(1导数的概念1(2导数的运算1(3导数在研究函数中的应用 1(4导数在实际生活中的应用 1(5定积分第2章推理与证明2(1合情推理与演绎推理 2(2直接证明与间接证明 2(3数学归纳法2(4公理化思想第3章数系的扩充与复数的引入6(1数系的扩充3(2复数的四则运算 3(3复数的几何意义 2-3第1章计数原理1(1两个基本原理1(2排列1(3组合1(4计数应用题1(5二项式定理第2章概率2(1随机变量及其概率分布 2(2超几何分布2(3独立性2(4二项分布2(5离散型随机变量的均值与方差2(6正态分布第3章统计案例3(1假设检验3(2独立性检验3(3线性回归分析4(4聚类分析我也是江苏高中文科生了.....现在读高三想想就要高考了啊所以我更加能体会到你的急迫得数学者得天下这是很正确的想要学好数学首先要吃透课本很多高考题都是来自于课本改编做了历年的江苏数学高考卷不难发现 160分总分基础分大概有100以上....所以基础很重要不要一味的抓难题把该做对的都做对争取不失分在这样的基础上逐渐提高做题的速度.....现在我们每天都会有小练习来练习速度...这样剩余的时间就是可以提高的部分.... 现在一轮复习速度不会很快也比较基础所以尽量跟老师走不懂得题目一定要想办法搞清楚不要有漏洞还有平常做的那些卷子要综合起来看看那些地方失分比较严重然后进行针对性的联系不要盲目买参考书做题那样不仅浪费时间而且效率也不高问:江苏很注重语数外，我的语文和英语，不比班级尖子生差，只是我数学，往往比他们少近20分，是数学，让我不够优秀。
