9.1 平面的基本性质(1)

课题：10.1平面的基本性质课题：10.1平面的基本性质【教学目标】1.知识目标：理解和掌握平面的三个基本性质，并学会应用性质进行一些简单的分析和判断。

2. 能力目标：通过实例和多媒体进行直观教学，培养学生的观察能力和空间想象能力。

通过应用性质进行一些简单的分析和判断，培养逻辑思维能力。

3.情感目标：（1）通过创设主题式故事情境，增强学习兴趣。

（2）结合生活，进行“数学来源于生活”的唯物主义观念教育。

（3）通过问题解决，培养学生合作交流、独立思考等良好的个性品质，以及勇于批判、敢于创新的科学精神。

【教学重点】平面的基本性质。

因为研究空间图形时，往往将有关点、线归结到一个平面内，再利用平面图形的性质解决。

所以要求学生对基本性质有较深刻的理解。

【教学难点】平面的基本性质的掌握与运用。

因为平面的基本性质既抽象又枯燥，而中职幼师专业的学生想象和思维都较弱，所以掌握与运用三个平面的基本性质会有一定的难度。

【教学方法】遵循学生的认知规律，结合多媒体将具体与抽象、感性与理性、动手与动脑有机地结合在一起。

进行思考、交流，师生共同讨论等学法。

根据中职学生想象能力、思维能力较弱的特点，尽量从直观入手，因此考虑通过创设既靠近生活，又体现数学本质，并且能从情感上激发学生主动、深入思考的有效情境（主题式故事情境）作为载体的启发式教法。

【教学过程】图9−5公理1作为判断和证明直线是否在平图9−8反映了只要“两面共一点”，就两面共一线，且过这一点，线唯把信封的一角竖立在桌面上，那么信封所在平面和桌面所在平面只交于一点，对吗？如图：在长方体ABCD—A1B1C1D1是棱A1B1上的中点，画出C1三点所确定的平面α与长方体表面的交线。

平面 (一)1-）；教学目标:初步了解平面的概念；了解平面的基本性质（公理3能正确使用集合符号表示有关点、线、面的位置关系；能运用平面的基本性质解决一些简单的问题．重点难点:正确使用集合符号表示点、线、面的位置关系，平面的基本性质引入新课1．平面的概念：光滑的桌面、平静的湖面等都是我们熟悉的平面形象，数学中的平面概念是现实平面加以抽象的结果．平面的特征：平面没有大小、厚薄和宽窄，平面在空间是无限延伸的．2．平面的画法：3．平面的表示方法：4．用数学符号来表示点、线、面之间的位置关系：点与直线的位置关系：点与平面的位置关系：直线与平面的位置关系：5．平面的基本性质：公理1：文字语言描述为：符号语言表示为：公理2：文字语言描述为：符号语言表示为：公理3：文字语言描述为：符号语言表示为：例题剖析1辨析：10个平面重叠起来，要比5个平面重叠起来厚．（）有一个平面的长是50米，宽是20米．（）黑板面是平面．（）平面是绝对的平，没有大小，没有厚度，可以无限延展的抽象的数学概念．（）2（1）点A 在平面α内，点B 不在平面α内，点A ，B 都在直线a 上；（2）平面α与平面β相交于直线m ，直线a 在平面α内且平行于直线m ．4 如图，ABC ∆中，若BC AB ，在平面α内，判断AC 是否在平面α内．巩固练习1．为什么许多自行车后轮旁只安装一只撑脚？2．四条线段顺次首尾相接，所得的图形一定是平面图形吗？3已知ABC ∆在平面α外，它的三边所在直线分别交平面α于点P 、Q 、R ，求证：P 、Q 、R 三点共线。

课题：9．1平面的基本性质(二)教学目的：1理解公理一、三,并能运用它解决点、线共面问题2理解公理二,并能运用它找出两个平面的交线及“三线共点”和“三点共线”问题教学重点：平面基本性质的三条公理及其作用．教学难点：（1）对“有且只有一个”语句的理解．（2）确定两相交平面的交线．授课类型：新授课课时安排：1课时教具：多媒体、实物投影仪内容分析：平面的基本性质是研究空间图形性质的理论基础，也是以后演绎推理的逻辑依据．平面的基本性质是通过三条公理及其重要推论来刻划的，通过这些内容的教学，使学生初步了解从具体的直观形象到严格的数学表述的方法，使学生的思维从直觉思维上升至分析思维，使学生的观念逐步从平面转向空间．本课以平面基本性质的三条公理及公理3的三个推论为主要内容，既有学生熟悉的事实，又有学生初次接触的证明，因此以“设问——实验——归纳”法和讲解法相结合的方式进行教学．首先，对于平面基本性质的三条公理，因为是“公理”，无需证明，教学中以系列设问结合模型示范引导学生共同思考、观察和实验，从而归纳出三条公理并加以验证．其中公理1应以直线的“直”和“无限延伸”来刻划平面的“平”和“无限延展”；公理2要抓住平面在空间的无限延展特征来讲；公理3应突出已知点的个数和位置，强调“三个点”且“不在同一直线上”．通过三条公理的教学培养学生的观察能力和空间观念，加深对“有且只有一个”语句的理解．对于公理3的三个推论的证明，学生是初次接触“存在性”和“唯一性”的证明，应引导学生以公理3为主要的推理依据进行分析，逐渐摆脱对实物模型的依赖，培养推理论证能力，证明过程不仅要进行口头表述，而且教师应进行板书，使学生熟悉证明的书写格式和符号．最后，无论定理还是推论，都要将文字语言转化为图形语言和符号语言，并且做到既不遗漏又不重复且忠于原意．教学过程：一、复习引入：1．平面的概念：平面是没有厚薄的，可以无限延伸，这是平面最基本的属性常见的桌面，黑板面，平静的水面等都是平面的局部形象一个平面把空间分成两部分，一条直线把平面分成两部分2．平面的画法及其表示方法：①在立体几何中，常用平行四边形表示平面当平面水平放置时，通常把平行四边形的锐角画成45，横边画成邻边的两倍画两个平面相交时，当一个平面的一部分被另一个平面遮住时，应把被遮住的部分画成虚线或不画②一般用一个希腊字母α、β、γ……来表示，还可用平行四边形的对角顶点的字母来表示如平面α，平面AC等3．空间图形是由点、线、面组成的点、线、面的基本位置关系如下表所示：Aα A α∈ 点A 在平面α内 A αA α∉ 点A 不在平面α内 b a A a b A =直线a 、b 交于A 点 a αa α⊂直线a 在平面α内 aα a α=∅ 直线a 与平面α无公共点a Aα a A α= 直线a 与平面α交于点Al αβ= 平面α、β相交于直线l集合中“∈”的符号只能用于点与直线，点与平面的关系，“⊂”和“ ”的符号只能用于直线与直线、直线与平面、平面与平面的关系，虽然借用于集合符号，但在读法上仍用几何语言． a α=∅或a A α=二、讲解新课：1 平面的基本性质立体几何中有一些公理，构成一个公理体系．人们经过长期的观察和实践，把平面的三条基本性质归纳成三条公理．公理 1 如果一条直线的两点在一个平面内，那么这条直线上的所有点都在这个平面内 推理模式：A AB B ααα∈⎫⇒⊂⎬∈⎭． 如图示： 或者：∵,A B αα∈∈，∴AB α⊂应用：这条公理是判定直线是否在平面内的依据，也可用于验证一个面是否是平面，如泥瓦工用直的木条刮平地面上的水泥浆．①判定直线在平面内；②判定点在平面内模式：a A A a αα⊂⎧⇒∈⎨∈⎩． 公理1说明了平面与曲面的本质区别．通过直线的“直”来刻划平面的“平”，通过直线的“无限延伸”来描述平面的“无限延展性”，它既是判断直线在平面内，又是检验平面的方法．公理2如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线推理模式：A A l A ααββ∈⎫⇒∈=⎬∈⎭ 如图示：BA α或者：∵,A A αβ∈∈，∴,l A l αβ=∈应用：①确定两相交平面的交线位置；②判定点在直线上公理2揭示了两个平面相交的主要特征，是判定两平面相交的依据，提供了确定两个平面交线的方法．指出:今后所说的两个平面(或两条直线),如无特殊说明,均指不同的平面(直线)公理3 经过不在同一条直线上的三点，有且只有一个平面推理模式：,, ,,,,A B C A B C A B C ααβ⎫⎪∈⇒⎬⎪∈⎭不共线与β重合或者：∵,,A B C 不共线，∴存在唯一的平面α，使得,,A B C α∈.应用：①确定平面；②证明两个平面重合“有且只有一个”的含义分两部分理解，“有”说明图形存在，但不唯一，“只有一个”说明图形如果有顶多只有一个，但不保证符合条件的图形存在，“有且只有一个”既保证了图形的存在性，又保证了图形的唯一性．在数学语言的叙述中，“确定一个”，“可以作且只能作一个”与“有且只有一个”是同义词，因此，在证明有关这类语句的命题时，要从“存在性”和“唯一性”两方面来论证．实例:(1)门:两个合页,一把锁；(2)摄像机的三角支架；(3)自行车的撑脚公理3及其下一节要学习的三个推论是空间里确定一个平面位置的方法与途径，而确定平面是将空间问题转化为平面问题的重要条件，这个转化使得立体几何的问题得以在确定的平面内充分使用平面几何的知识来解决，是立体几何中解决相当一部分问题的主要的思想方法．2 平面图形与空间图形的概念如果一个图形的所有点都在同一个平面内，则称这个图形为平面图形，否则称为空间图形例1 求证:三角形是平面图形已知：三角形ABC求证：三角形ABC是平面图形证明：∵三角形ABC的顶点A、B、C不共线∴由公理3知，存在平面α使得A、B、Cα∈再由公理1知，AB、BC、CAα⊂∴三角形ABC上的每一个点都在同一个平面内∴三角形ABC 是平面图形例2 点A ∉平面BCD ，,,,E F G H 分别是,,,AB BC CD DA 上的点，若EH 与FG 交于（这样的四边形ABCD 就叫做空间四边形） 求证：P 在直线BD 上 证明：∵EH FG P =，∴P EH ∈，P FG ∈，∵,E H 分别属于直线,AB AD ，∴EH ⊂平面ABD ，∴P ∈平面ABD ，同理：P ∈平面CBD ，又∵平面ABD 平面CBD BD =，所以，P 在直线BD 上四、课堂练习：1 下面是一些命题的叙述语（A 、B 表示点，a 表示直线，α、β表示平面）A ．∵αα∈∈B A ,，∴α∈AB ． B ．∵βα∈∈a a ,，∴a =βα ．C ．∵α⊂∈a a A ,，∴A α∈．D ．∵α⊂∉a a A ,，∴α∉A ．其中命题和叙述方法都正确的是（ ）2．下列推断中，错误的是（ ）A ．ααα⊂⇒∈∈∈∈lB l B A l A ,,,B ．B B A A =⇒∈∈∈∈βαβαβα ,,,C ．αα∉⇒∈⊄A l A l ,D ．βα∈∈C B A C B A ,,,,,，且A 、B 、C 不共线βα,⇒重合3．一个平面把空间分成____部分，两个平面把空间最多分成____部分，三个平面把空间最多分成____部分．4．判断下列命题的真假，真的打“√”，假的打“×”（1）空间三点可以确定一个平面 （ ）（2）两条直线可以确定一个平面 （ ）（3）两条相交直线可以确定一个平面 （ ）（4）一条直线和一个点可以确定一个平面 （ ）（5）三条平行直线可以确定三个平面 （ ）（6）两两相交的三条直线确定一个平面 （ ）（7）两个平面若有不同的三个公共点，则两个平面重合（ ）（8）若四点不共面，那么每三个点一定不共线 （ ）5．看图填空（1）AC ∩BD =（2）平面AB 1∩平面A 1C 1=（3）平面A 1C 1CA ∩平面AC =（4）平面A 1C 1CA ∩平面D 1B 1BD =（5）平面A 1C 1∩平面AB 1∩平面B 1C =（6）A 1B 1∩B 1B ∩B 1C 1=答案：1. C 2. C 3. 2,4,8 4. ⑴×⑵×⑶√⑷×⑸×⑹×⑺×⑻√5.⑴O ⑵A 1B 1⑶O ⑷OO 1⑸B 1⑹B 1五、小结 ：本课主要的学习内容是平面的基本性质，三条公理中公理1用于判定直线是否在平面内，公理2用于判定两平面相交，公理3是确定平面的依据．“确定一个平面”与“有且只有一个平面”是同义词．“有”即“存在”，“只有一个”即“唯一”．所以证明有关“有且只有一个”语句的命题时，要证两方面——存在性和唯一性．证A 1明的方法是反证法和同一法六、课后作业：七、板书设计（略）八、课后记：。

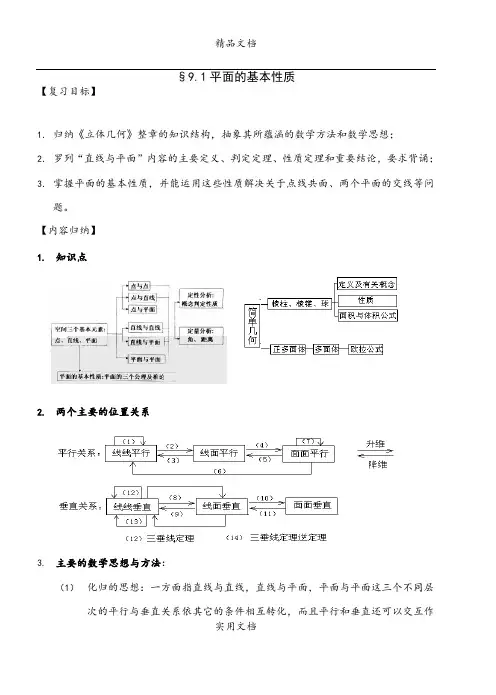
§9.1平面的基本性质【复习目标】1．归纳《立体几何》整章的知识结构，抽象其所蕴涵的数学方法和数学思想；2．罗列“直线与平面”内容的主要定义、判定定理、性质定理和重要结论，要求背诵；3．掌握平面的基本性质，并能运用这些性质解决关于点线共面、两个平面的交线等问题。

【内容归纳】1.知识点2.两个主要的位置关系3.主要的数学思想与方法：（1）化归的思想：一方面指直线与直线，直线与平面，平面与平面这三个不同层次的平行与垂直关系依其它的条件相互转化，而且平行和垂直还可以交互作实用文档用产生交互关系；另一方面指将复杂的空间图形化归为基本的空间图形，或将空间问题化归为平面几何的问题来解决，在立体几何的综合计算中，这一点尤为重要；（2）分类讨论的思想；空间的元素的关系按某种标准进行分类，是位置关系论证的基础；（3）几何计算中应注意“割”、“补”、“等积变换”等转化手段。

4.学习中的能力培养（1）丰富的空间想象能力：会识图、利用图形思考，掌握空间图形的简单变换并进行必要的转化；或借助于典型几何体——正四面体、正方体等，它们是空间几何体的基本结构，往往隐含于一些复杂的几何体中，善于从纷乱的空间图形中，抓住基本结构，常常是解立体几何的关键；（2）严密的逻辑思维和论证能力：想得清楚，说得明白，写得严谨；（3）文字语言、图形语言、符号语言的运用与转化的能力：（4）计算能力：掌握计算空间的距离和角的常用方法，做到“作图合理、论证到位、计算准确，方法合理。

5．平面的基本性质（三个公理及三个推论）（1）如果一条直线上有两点在一个平面内，那么这条直线上所有的点都在这个平面内；（2）如果两个平面有一个公共点，那么它们有且仅有一条通过这点的公共直线；（3）经过不在同一直线上的三点，有且仅有一个平面；推论1：经过一条直线和这条直线外一点，有且仅有一个平面；推论2：经过两条相交直线，有且仅有一个平面；实用文档实用文档推论3：经过两条平行直线，有且仅有一个平面；【典型例题】例1 判断下列命题的正误：（1） 首尾相结的四条线段在同一个平面内；（ ）（2） 三条互相平行的线段在同一个平面内；（ ）（3） 两两相交的三条直线在同一个平面内；（ ）（4） 若四个点中的三个点在同一条直线上，那么这四个点在同一个平面内；（ ）（5） 互相垂直的两条直线，有且仅有一个公共点；（ ）（6） 经过一点有且仅有一条直线垂直于已知直线；（ ）（7） 垂直于同一条直线的两条直线平行；（ ）（8） 两平行线之一垂直于一直线，则另一条也垂直于此直线；（ ）（9） 若,A l A α∈∈，,B l B α∈∈，则l α⊂；（ ）（10） 若,A A αβ∈∈，,B B αβ∈∈，则AB αβ⋂=；（ ）（11） 若,l A l α⊄∈，则A α∉；（ ）（12） 若,,A B C α∈，,,A B C β∈，且,,A B C 不共线，则α与β重合.（ ） 例2 已知正方体1AC 中，E 、F 分别为11C D 、11C B 中点，AC ∩BD=P ，Q EF C A = 11，求证：（1）D 、B 、F 、E 四点共面；（2）若C A 1交平面DBFE 于R 点，则P 、Q 、R 三点共线。

平面的基本性质【教学目标】1.会用符号语言规范地表述空间点、直线、平面之间的位置关系．2.理解关于平面的三个公理和三个推论【重点、难点】能用图形、文字、符号三种语言描述三个公理，理解关于平面的三个公理和三个推论．【核心素养】1. 通过对空间点、线、面位置关系的学习，培养学生直观想象素养．2．借助于三个基本事实与推论的应用，培养学生逻辑推理素养.【新课讲解】(1)平面的基本性质①公理1：过不在一条直线上的三点，有且只有一个平面．基本事实1也可简单地说成，不共线的三点确定一个平面．②公理2：如果一条直线上的两个点在一个平面内，那么这条直线在这个平面内． 用符号表示为：⎭⎬⎫A ∈αB ∈α⇒AB ⊂α. ③公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线． 用符号表示为： ⎭⎬⎫P ∈αP ∈β⇒α∩β＝l 且P ∈l . (2)基本公理的推论①推论1：经过一条直线和这条直线外的一点，有且只有一个平面． ②推论2：经过两条相交直线，有且只有一个平面．③推论3：经过两条平行直线，有且只有一个平面．【深入学习】例．下列说法正确的是( )A ．三点可以确定一个平面B ．一条直线和一个点可以确定一个平面C ．四边形是平面图形D ．两条相交直线可以确定一个平面D [A 错误，不共线的三点可以确定一个平面．B 错误，一条直线和直线外一个点可以确定一个平面．C 错误，四边形不一定是平面图形．D正确，两条相交直线可以确定一个平面．]例2．证明：两两相交且不共点的三条直线在同一平面内．[解]已知：如图所示，l1∩l2＝A，l2∩l3＝B，l1∩l3＝C．求证：直线l1，l2，l3在同一平面内．法一：∵l1∩l2＝A，∴l1和l2确定一个平面α.∵l2∩l3＝B，∴B∈l2.又∵l2⊂α，∴B∈α.同理可证C∈α.又∵B∈l3，C∈l3，∴l3⊂α.∴直线l1，l2，l3在同一平面内．法二：∵l1∩l2＝A，∴l1，l2确定一个平面α.∵l2∩l3＝B，∴l2，l3确定一个平面β.∵A∈l2，l2⊂α，∴A∈α.∵A∈l2，l2∈β，∴A∈β.同理可证B∈α，B∈β，C∈α，C∈β.∴不共线的三个点A，B，C既在平面α内，又在平面β内．∴平面α和β重合，即直线l1，l2，l3在同一平面内．。