2020最新版QC七大手法之直方图教材
- 格式:pptx
- 大小:597.50 KB
- 文档页数:39



QC七大手法-直方图一、什么是QC七大手法QC(Quality Control)七大手法是一种常用于解决质量问题和提高产品质量的方法。
它包含了七种常用的统计学手法,分别是:直方图、控制图、散点图、因果图、帕累托图、箱线图和流程图。
这些手法可以帮助我们分析和解决质量问题,以达到质量改进的目的。
本文将重点介绍其中一种手法——直方图。
二、直方图的基本概念直方图是一种用于显示数据分布情况的图表。
它通过将数据划分为一系列间隔,然后统计每个间隔内数据出现的频率,最终通过矩形条来呈现数据的分布情况。
直方图通常用于展示连续变量或离散变量的频率分布,可以帮助我们了解数据的分布规律和集中趋势。
三、绘制直方图的步骤1. 数据收集首先,我们需要收集相关的数据。
这些数据可以是产品的尺寸数据、质量数据或其他与质量有关的数据。
2. 数据整理在绘制直方图之前,我们需要对数据进行整理和分类。
将数据按照一定的规则进行分组,并记录每组数据的频数。
3. 确定间隔和组数在进行数据分组时,我们需要确定数据的间隔和组数。
间隔一般是根据数据的最大值和最小值来确定的,组数可以根据实际情况进行调整。
4. 绘制直方图绘制直方图可以使用各类数据分析软件、编程语言或绘图工具。
在绘图时,我们需要将每组数据的频数表示为相应的矩形条,并将矩形条按照一定的间隔排列。
5. 添加标题和注解为了使直方图更具可读性,我们可以添加标题和注解。
标题可以简要描述直方图的目的和内容,注解可以解释数据的分布情况和统计指标。
6. 分析直方图通过观察直方图,我们可以了解数据的分布情况和集中趋势。
例如,我们可以通过直方图来判断数据是正态分布、偏态分布还是离散分布。
同时,我们还可以通过直方图来确定数据的中位数、均值和标准差等统计指标。
四、直方图在QC中的应用直方图在QC中有广泛的应用,可以帮助我们分析和解决质量问题。
以下是直方图在QC中的一些常见应用场景:1. 检测质量问题通过绘制产品尺寸、质量或其他相关数据的直方图,我们可以快速发现质量问题。



频数 (频率)直方图二、频数 (频率)直方图(一) 直方图的作法为研究一批产品的质量情况,需要研究它的某个质量特性 (这里为了叙述简单起见,仅讨论一个质量特性,有必要时也可以同时讨论多个质量特性)X的变化规律。
为此,从这批产品(总体)中抽取一个样本 (设样本量为n),对每个样本产品进行该特性的测量 (观测)后得到一组样本观测值,记为x1,x2,…,x n,这便是我们通常说的数据。
为了研究数据的变化规律,需要对数据进行一定的加工整理。
直方图是为研究数据变化规律而对数据进行加工整理的一种基本方法。
下面用一个例子来说明直方图的概念及其作法。
[例1.3-3]食品厂用自动装罐机生产罐头食品,从一批罐头中随机抽取100个进行称量,获得罐头的净重数据如下:342 352 346 344 343 339 336 342 347 340 340 350 347 336 341 349 346 348 342 346 347 346 346 345 344 350 348 352 340 356 339 348 338 342 347 347 344 343 349 341 348 341 340 347 342 337 344 340 344 346 342 344 345 338 351 348 345 339 343 345 346 344 344 344 343 345 345 350 353 345 352 350 345 343 347 354 350 343 350 344 351 348 352 344 345 349 332 343 340 346 342 335 349 348 344 347 341 346 341 342为了解这组数据的分布规律,对数据作如下整理:(1)找出这组数据中的最大值x max,及最小值x min,计算它们的差R=x max -x min ,R称为极差,也就是这组数据的取值范围。

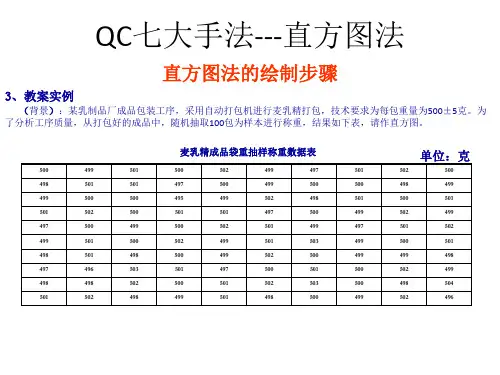

直方图1、概念直方图是指:将某期间所收集的计量值数据(如:尺寸、重量、硬度……等)经分组整理成次数分 配表,并以柱形予以图形化,以掌握这些数据所代表的情报。
直方图主要应用于:展示过程的分布情况. 图1表示了直方图的基本形状。
2、直方图的制作步骤A 、收集数据,至少要收集50〜100个数据;B 、参照下表确定组数(或用N 的平方根确定):表1分组对照表C 、确定组距(a )、找出最大数据X max 和最小数据X min ;(b )、求全距R 。
区=最大数据X max —最小数据X min (注:异常值除外); (c )、求组距C 。
C 二全距R :组数K ;(d)、从测定单位的整数倍之数据中,找出接近的C 值的适当数据作为组距。
D 、决定各组参数及次数分配表(a )、取数据最小测量单位的1/2为组界值的单位; (b )、第一个境界值=最小值-1/2X 最小测量单位;第二个境界值=第一个境界值+组距; 第三个境界值=第二个境界值+组距; 其它依此类推。
(c )、求各组之中心值。
该组之上组界(较大组界值)+该组这组界(较小组界值)中心值二 -------------------------------------------------21次数(d)、制作次数分配表。
如下表:表2次数分配表E X轴的最大值与最小值之间以等长度标出刻度。
如图2:直方图图2直方图F、在图上标出图名,记入搜集数据的时间和其他必要的记录。
总次数(频数1统计特征值X平均值)与S(标准偏差)是直方图上的重要数据,一定要标出.3、直方图的作用①、由图形可以比较容易掌握制程的全貌(如:中心趋势,离散趋势,分配形状);②、可了解制程的安定或异常状况;③、与规格进行比较可判断制程能力。
4、直方图的常见分布形状图3常态型直方图蔓延。
图5离岛型直方图④、双峰型--制程分布有两个高峰,表示制程为两种不同分配组合,需进行层别。
图6双峰型直方图⑤、缺齿型一一制程分布参差不齐,表示制程呈不正常分配,可能是:--测量问题,如:测量有偏差、数字四舍五入;——分组不恰当(如数据太少或组数太多);——数据有修改或伪造。

QC七大手法(一)-—直方图的制作直方图的作用:展示过程的分布情况,了解总体数据的中心和变异,并推测发展趋势.步骤一:搜集数据n,全部均匀的加以随机抽样.所搜集的数据应大于50以上.138 142 145 140 141 步骤二:找出最大值L和最小值S139 140 141 138 138 139 最大值L=148 最小值S=121144 138 139 136 137 137 步骤三:求全距(R)=最大值—最小值又叫极差131 127 138 137 137 133 R = L —S = 148 —121 = 27140 130 136 138 138 132 步骤四:决定组数K145 141 135 131 136 131 (1)其为: k=1+3.32log n n = 60134 136 137 133 134 132 (2) 公式一般对数据之分组可参照下表:135 134 132 134 129 数据数组数137 132 130 135 135 134 ~50 5~7136 131 131 139 136 135 51~100 6~10 例:取7组102~250 7~12250~10~20步骤五:求组距(h) (1 )组距=全距÷组数(h =R÷K)(2 )为便于计算平均数及标准差,组距常取为2,5或10的倍数。
例:h =27/7 =3.86, 组距取4 = 组界步骤六:求各组上组界,下组界(由小而大顺序)(1)第一组下组界=最小值—(最小测定单位/ 2 )第一组上组界=第一组下组界+组界第二组下组界=第一组上组界(2)最小测定单位整数位之最小测定单位1 小数点1位之最小测定单位为0。
1小数点2位之最小测定单位为0.01(3)最小数应在最小一组内,最大数应在最大一组内; 若有数字小于最小一组下组界或大于最大一组上组界值时,应自动加一组。
例:第一组=121—1/2=120.5~124.5 第二组=124.5~128.5 第三组=128.5~132.5第四组=132.5~136.5 第五组=136.5~140。
QC七大手法之直方圖教育訓練講義一、何謂直方圖?將所彙集的數據、特性值或結果值,用一定的範圍在橫軸上加以分成幾個相等的區間,將各區間內的測定值所出現的次數累積起來的面積用柱型畫出的圖形。
二、目的直方圖可以了解產品在規格標準之下分布的型態、製程的中心值與差異的大小等情形。
三、實施步驟1彙集數據並且紀錄在紙上彙集數據時對於抽樣分佈必須特別注意,不可指取某些部份樣品,應就全部均勻的加以抽查。
數據的彙集最好在50~100組之間。
2.找出數據中最大值與最小值將最大值與最小值分別找出,紀錄在每行底列,再根據底列的數據找出全體的最大值與最小值。
3.計算全距(R)R=最大值-最小值4.決定組數與組距組數就是直方圖柱型數量,組數的計算是根據數量的多寡來決定。
可由數據分組數參考表(表1),即可決定組數。
表1另外也可以用公式計算。
公式:組數(K)=1+3.23log n組距的計算方式:組距=全距÷組數為了方便計算平均數與標準差,組距通常是2、5或10的倍數。
5.決定各組的上組界與下組界組界的決定由最小一組的下組界為基準以下列公式求出:最小一組的下組界=全部數據的最小值-量測值最小位數(一般是1)×0.5 最小一組的上組界=最小一組的下組界+組距最小二組的下組界=最小一組的上組界如此各組依此類推,計算到最大一組的上組界。
6.決定組的中心點計算方式:(上組界+下組界)÷2 =組的中心點1.製作次數分配表將所有的數據依照數值的大小記入各組的組界內,然後計算各組界的次數。
2.製作直方圖以橫軸表示測量值的變化,縱軸表示次數,橫軸與縱軸取出適當的長度標上記號,然後將各組的組界分別標示在橫軸上,各組次數的多少則用柱型畫在各組距上,柱與柱之間不能有間隙,如此就完成直方圖。
可在空白處填上主題、規格、平均值、數據來源、日期等資料。
一、注意事項1.直方圖可根據山型圖案分佈形狀來觀察製品工程是否正常。
2.產品規格分佈圖案可與目標、標準規格做比較,看看是否差異過大。