SPSS回归分析作业
- 格式:doc
- 大小:564.00 KB
- 文档页数:22

回归分析实验内容:基于居民消费性支出与居民可支配收入的简单线性回归分析【研究目的】居民消费在社会经济的持续发展中有着重要的作用。
影响各地区居民消费支出的因素很多,例如居民的收入水平、商品价格水平、收入分配状况、消费者偏好、家庭财产状况、消费信贷状况、消费者年龄构成、社会保障制度、风俗习惯等等。
为了分析什么是影响各地区居民消费支出有明显差异的最主要因素,并分析影响因素与消费水平的数量关系,可以建立相应的经济模型去研究。
【模型设定】我们研究的对象是各地区居民消费的差异。
由于各地区的城市与农村人口比例及经济结构有较大差异,现选用城镇居民消费进行比较。
模型中被解释变量Y选定为“城市居民每人每年的平均消费支出”。
从理论和经验分析,影响居民消费水平的最主要因素是居民的可支配收入,故可以选用“城市居民每人每年可支配收入”作为解释变量X,选取2010年截面数据。
1、实验数据表1:2010年中国各地区城市居民人均年消费支出和可支配收入数据来源:《中国统计年鉴》2010年2、实验过程作城市居民家庭平均每人每年消费支出(Y)和城市居民人均年可支配收入(X)的散点图,如图1:从散点图可以看出居民家庭平均每人每年消费支出(Y)和城市居民人均年可支配收入(X)大体呈现为线性关系,所以建立如下线性模型:Y=a+bX表2模型汇总b模型R R方调整R方标准估计的误差1 .965a.932 .930 877.29128a.预测变量:(常量),可支配收入X(元)。
b.因变量:消费性支出Y(元)表3相关性表4系数a3、结果分析表2模型汇总:相关系数为0.965,判定系数为0.932,调整判定系数为0.930,估计值的标准误877.29128表3是相关分析结果。
消费性支出Y与可支配收入X相关系数为0.965,相关性很高。
表4是回归分析中的系数:常数项b=704.824,可支配收入X 的回归系数a=0.668。
a的标准误差为0.034,回归系数t的检验值为19.921,P值为0,满足95%的置信区间,可认为回归系数有显著意义。

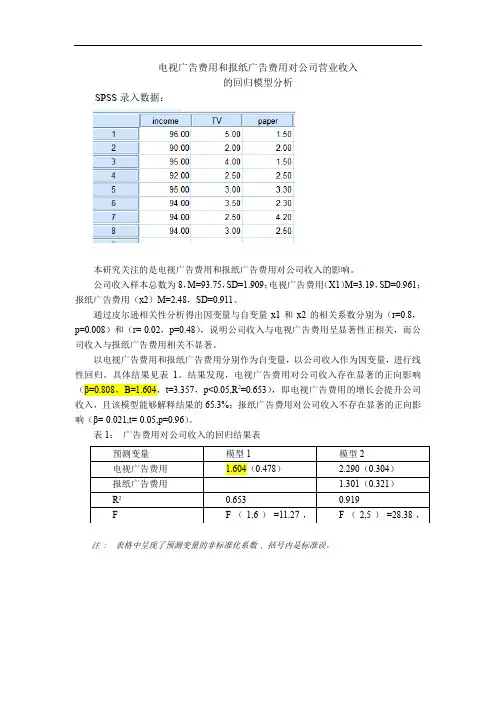
电视广告费用和报纸广告费用对公司营业收入的回归模型分析SPSS录入数据:本研究关注的是电视广告费用和报纸广告费用对公司收入的影响。
公司收入样本总数为8,M=93.75,SD=1.909;电视广告费用(X1)M=3.19,SD=0.961;报纸广告费用(x2)M=2.48,SD=0.911。
通过皮尔逊相关性分析得出因变量与自变量x1和x2的相关系数分别为(r=0.8,p=0.008)和(r=-0.02,p=0.48),说明公司收入与电视广告费用呈显著性正相关,而公司收入与报纸广告费用相关不显著。
以电视广告费用和报纸广告费用分别作为自变量,以公司收入作为因变量,进行线性回归。
具体结果见表1。
结果发现,电视广告费用对公司收入存在显著的正向影响(β=0.808,B=1.604,t=3.357,p<0.05,R2=0.653),即电视广告费用的增长会提升公司收入,且该模型能够解释结果的65.3%;报纸广告费用对公司收入不存在显著的正向影响(β=-0.021,t=-0.05,p=0.96)。
表1:广告费用对公司收入的回归结果表注: 表格中呈现了预测变量的非标准化系数, 括号内是标准误。
以电视广告费用和报纸广告费用同时作为自变量,以公司收入作为因变量,则两个费用对公司收入存在显著的正向影响(β电视=1.153,B电视=2.29,t=7.532,p<0.05;β报纸=0.621,B报纸=1.301,t=4.057,p<0.052, R2=0.919),即电视广告和报纸广告费用的同时增长会提升公司收入,且该模型能够解释结果的91.9%。
共线性分析:VIF电视广告=1.448,VIF报纸广告=1.448,均小于5,说明电视广告和报纸广告之间共线性可能性较低。
思路及步骤:1、公司收入样本总数为8,M=93.75,SD=1.909;电视广告费用M=3.19,SD=0.961;报纸广告费用M=2.48,SD=0.911。

SPSS作业6:回归分析(一)回归分析多元线性回归模型的基本操作:(1)选择菜单Analyze-Regression-Linear;(2)选择被解释变量(能源消费标准煤总量)和解释变量(国内生产总值、工业增加值、建筑业增加值、交通运输邮电业增加值、人均电力消费、能源加工转换效率)到对应框中;(3)在Method框中,选择Enter方法;在Statistics框中,选择Estimates、Model fit、Covariancematrix、Collinearity diagnostics选项;在Plots框中,选择ZRESED到Y框,ZPRED到X框,再选择Histogram和Normal plot;(4)选择菜单Analyze-Non Test-1-Sanple K-S;选择菜单Analyze-Correlate-Brivariate;结果如下:Regression能源消费需求的多元线性回归分析结果(强制进入策略)(一)Model Summary bModel R R Square Adjusted R Square Std. Error of the Estimate1 .990a.980 .973 8480.38783a. Predictors: (Constant), 能源加工转换效率/%, 交通运输邮电业增加值/亿元, 工业增加值/亿元, 人均电力消费/千瓦时, 建筑业增加值/亿元, 国内生产总值/亿元b. Dependent Variable: 能源消费标准煤总量/万吨分析:被解释变量和解释变量的复相关系数为0.990,判定系数为0.980,调整的判定系数为0.973,回归方程的估计标准误差为8480.38783。
该方程有6个解释变量,调整的判定系数为0.973,,接近于1,所以拟合优度较高,被解释变量可以被模型解释的部分较多,未能解释的部分较少。
分析:由上可知,被解释变量的总离差平方和为5.882E10,回归平方和及均方分别为5.766E10和9.611E9,剩余平方和及均方分别为1.151E9和7.192E7,F检验统计量的观测值为133.636,对应的概率p值近似为0。

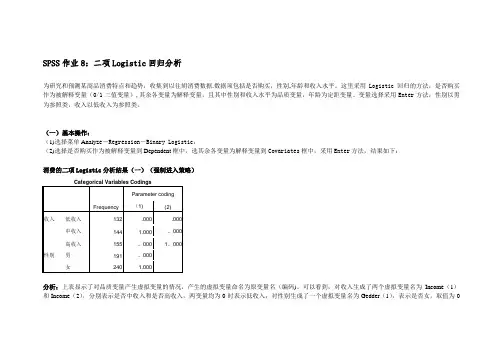
SPSS作业8:二项Logistic回归分析为研究和预测某商品消费特点和趋势,收集到以往胡消费数据.数据项包括是否购买,性别,年龄和收入水平。
这里采用Logistic回归的方法,是否购买作为被解释变量(0/1二值变量),其余各变量为解释变量,且其中性别和收入水平为品质变量,年龄为定距变量。
变量选择采用Enter方法,性别以男为参照类,收入以低收入为参照类。
(一)基本操作:(1)选择菜单Analyz e-Regression-Binary Logistic;(2)选择是否购买作为被解释变量到Dependent框中,选其余各变量为解释变量到Covariates框中,采用Enter方法,结果如下:消费的二项Logistic分析结果(一)(强制进入策略)Categorical Variables CodingsFrequency Parameter coding (1) (2)收入低收入132 .000 .000中收入144 1.000 。
000高收入155 。
000 1。
000性别男191 。
000女240 1.000分析:上表显示了对品质变量产生虚拟变量的情况,产生的虚拟变量命名为原变量名(编码)。
可以看到,对收入生成了两个虚拟变量名为Income(1)和Income(2),分别表示是否中收入和是否高收入,两变量均为0时表示低收入;对性别生成了一个虚拟变量名为Gedder(1),表示是否女,取值为0时表示为男。
消费的二项Logistic 分析结果(二)(强制进入策略)Block 0: Beginning BlockClassification Table a,bObserved Predicted是否购买 Percentage Correct不购买购买Step 0是否购买不购买 269 0 100。
购买162。
0 Overall Percentage62。
4a 。
Constant is included in the model 。
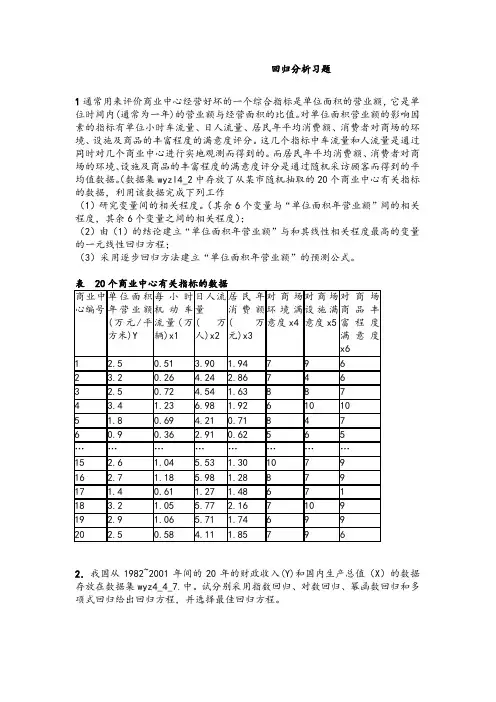
回归分析习题1通常用来评价商业中心经营好坏的一个综合指标是单位面积的营业额,它是单位时间内(通常为一年)的营业额与经营面积的比值。
对单位面积营业额的影响因素的指标有单位小时车流量、日人流量、居民年平均消费额、消费者对商场的环境、设施及商品的丰富程度的满意度评分。
这几个指标中车流量和人流量是通过同时对几个商业中心进行实地观测而得到的。
而居民年平均消费额、消费者对商场的环境、设施及商品的丰富程度的满意度评分是通过随机采访顾客而得到的平(数据集wyzl4_2中存放了从某市随机抽取的20个商业中心有关指标均值数据。
的数据,利用该数据完成下列工作(1)研究变量间的相关程度。
(其余6个变量与“单位面积年营业额”间的相关程度,其余6个变量之间的相关程度);(2)由(1)的结论建立“单位面积年营业额”与和其线性相关程度最高的变量的一元线性回归方程;(3)采用逐步回归方法建立“单位面积年营业额”的预测公式。
2.我国从1982~2001年间的20年的财政收入(Y)和国内生产总值(X)的数据存放在数据集wyz4_4_7.中。
试分别采用指数回归、对数回归、幂函数回归和多项式回归给出回归方程,并选择最佳回归方程。
1. 解:(1)变量间的相关性分析利用SPSS 软件构造所有变量的散点图矩阵和相关矩阵,结果见图1和表1 从散点图矩阵直观可以看出Y “单位面积年营业额”与x2“日人流量 (万人) ”和x3“居民年消费额(万元) ”线性关系较密切。
x2“日人流量 (万人) ”与x6 “对商场商品丰富程度满意度” 线性关系较密切从表1得)3,(x y ρ=0.795**,)2,(x y ρ=0.790**,)6,(x y ρ=.0 .697**, 说明 Y “单位面积年营业额”与x3“居民年消费额(万元) ”,x2“日人流量 (万人) ”,x6 “对商场商品丰富程度满意度”及x5 “对商场设施满意度”在0 .01 水平(双侧)上显著相关线性关。
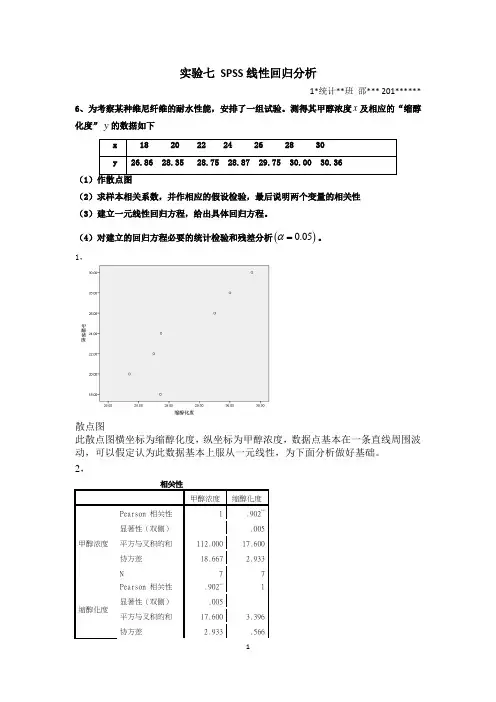
实验七 SPSS 线性回归分析1*统计**班 邵*** 201******6、为考察某种维尼纤维的耐水性能,安排了一组试验。
测得其甲醇浓度x 及相应的“缩醇化度”y 的数据如下(1(2)求样本相关系数,并作相应的假设检验,最后说明两个变量的相关性 (3)建立一元线性回归方程,给出具体回归方程。
(4)对建立的回归方程必要的统计检验和残差分析()0.05α=。
1,散点图此散点图横坐标为缩醇化度,纵坐标为甲醇浓度,数据点基本在一条直线周围波动,可以假定认为此数据基本上服从一元线性,为下面分析做好基础。
2,相关性甲醇浓度缩醇化度甲醇浓度Pearson 相关性 1.902**显著性(双侧).005平方与叉积的和 112.000 17.600 协方差 18.6672.933N7 7 缩醇化度Pearson 相关性.902**1显著性(双侧) .005 平方与叉积的和 17.600 3.396 协方差2.933.566N 7 7**. 在 .01 水平(双侧)上显著相关。
相关性检验-Pearson简单相关系数原假设:认为甲醇浓度和缩醇化度不存在线性关系。
从表中可知,甲醇浓度和缩醇化度的简单相关系数是0.902。
他们的相关系数检验的P值为0.005,因此,给定显著性水平为0.05或0.01时,都应该拒绝原假设,认为两总体存在线性关系。
相关系数旁两个(**)是说明这两个变量的相关性很强。
总之,甲醇浓度和缩醇化度从在极强的正的线性相关性。
建立一元线性模型Y=A+BX原假设:变量甲醇浓度的偏回归系数与0无显著差异。
此表各数列数据项的含义依次为:偏回归系数,对应的概率P值,偏回归系数的标准误,标准化的偏回归系数,回归系数显著性检验中T的观测值,对应的概率p值,解释变量的容忍度和方差膨胀因子。
依据该表可以进行回归系数显著性检验,写出回归方程Y=25.506+0.157X该表还可以检验相关系数的显著性,甲醇浓度的P值为0.005,在显著水平为0.05或0.01下,都应拒绝原假设,认为变量甲醇浓度的偏回归系数与0有显著差异。

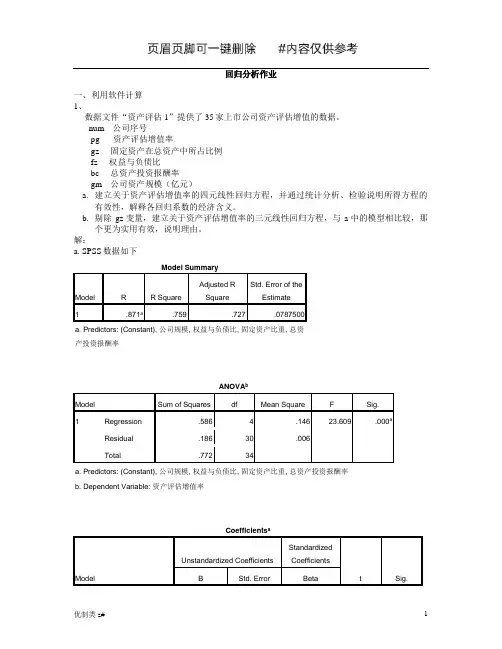
回归分析作业一、利用软件计算1、数据文件“资产评估1”提供了35家上市公司资产评估增值的数据。
num---公司序号pg---- 资产评估增值率gz----固定资产在总资产中所占比例fz----权益与负债比bc----总资产投资报酬率gm---公司资产规模(亿元)a.建立关于资产评估增值率的四元线性回归方程,并通过统计分析、检验说明所得方程的有效性,解释各回归系数的经济含义。
b.剔除gz变量,建立关于资产评估增值率的三元线性回归方程,与a中的模型相比较,那个更为实用有效,说明理由。
解:a.SPSS数据如下Model SummaryModel R R Square Adjusted RSquareStd. Error of theEstimate1 .871a.759 .727 .0787500a. Predictors: (Constant), 公司规模, 权益与负债比, 固定资产比重, 总资产投资报酬率ANOVA bModel Sum of Squares df Mean Square F Sig.1 Regression .586 4 .146 23.609 .000aResidual .186 30 .006Total .772 34a. Predictors: (Constant), 公司规模, 权益与负债比, 固定资产比重, 总资产投资报酬率b. Dependent Variable: 资产评估增值率Coefficients aModel Unstandardized CoefficientsStandardizedCoefficientst Sig.B Std. Error Beta1 (Constant) .396 .145 2.736 .010固定资产比重.079 .082 .092 .972 .339权益与负债比.062 .016 .416 3.918 .000总资产投资报酬率.602 .130 .493 4.618 .000公司规模-.044 .014 -.304 -3.201 .003 a. Dependent Variable: 资产评估增值率Residuals Statistics aMinimum Maximum Mean Std. Deviation NPredicted Value -.084652 .494055 .172240 .1312429 35Residual -1.5000236E-1.1493797 .0000000 .0739727 35Std. Predicted Value -1.957 2.452 .000 1.000 35Std. Residual -1.905 1.897 .000 .939 35a. Dependent Variable: 资产评估增值率由Model Summary和ANOVA表可知,R为0.871,决定系数R2为0.759,校正决定系数为0.727。
回归分析一.实验描述:中国民航客运量的回归模型。
为了研究我国民航客运量的变化趋势及其成因,我们以民航客运量作为因变量Y,以国民收入(X1)、消费额(X2)、铁路客运量(X3)、民航航线里程(X4)、来华旅游入境人数(X5)、为主要影响因素。
数据如下表。
试建立Y与X1--X5之间的多元线性回归模型。
二.实验过程描述及实验结果(1)该表格中输出了5个自变量和1个因变量的一般统计结果,包括各自变量与因变量的平均值,标准差和个案数16。
该表格中列出了各个变量之间的相关性,从该表格可以看出因变量Y和自变量X1之间的相关系数为0.989,相关性最大,。
因变量Y与自变量X3之间相关系数为0.227,相关性最小。
(3)该表格输出的是被引入或从回归方程中被剔出的各变量。
说明进行线性回归分析时所采用的方法是全部引入法Enter。
因变量为Y。
(4)该表格输出的是常用统计量。
从该表看出相关性系数R为0.999,判定系数R2为0.998,调整的判定系数为0.997,回归估计的标准误差为49.49240。
该表格输出的是方差分析表。
从这部分结果看出:统计量F为1.128E3;相伴概率值小于0.01,拒绝原假设说明多个自变量与因变量Y之间存在线性回归关系。
Sum of Squares一栏中分别代表回归平方和(1.382E7),残差平方和(24494.981)以及总平方和(1.384E7),df为自由度。
判定系数R2=0.99855。
该表格为回归系数分析。
其中Unstandardized Coefficients为非标准化系数,Standardized Coefficients为标准化系数,t为回归系数检验统计量,sig为相伴概率值。
由表知t检验的相伴概率值均小于0.01,拒绝原假设,说明个变量与因变量之间均有显著线性相关关系。
从表格中可以看出该多元线性回归方程为:y=450.909+0.354 X1-0.561 X2-0.007 X3+21.578 X4+0.435 X5该表格为残差统计结果表。
国家失业率GDP增长率
美 5.8 3.2
日 2.1 5.6
法 6.1 3.5
德 3.0 4.5
解:
一元线性回归模型
各种检验结果如下:
(一)相关系数r
标准误差17
判定系数,相关系数
存在与有显著性的线性相关
(二)回归系数显著性检验(t检验)
的t检验值分别为 6.897和 -4.429
显著性水平(sig)分别为 0.0062和 0.021 都小于 0.05
因此检验通过,也可查(自由度为 5-2=3),因为都大于 3.182
从而t检验通过
(三)F检验
F检验值为19.6163 显著性水平为 0.0214,小于0.05,因此 F检验通过也可查F分布表的得
F检验值大于(1,3)
F检验通过
(四)DW统计量(用来检验之间是否存在自相关的一种方法)
DW 检验值为 3.0723
4-DW=0.9237 不能确定是否具有自相关(有自相关不可拿来进行预测)
综上所诉,所得模型可以用来预测
当时 y=6.37。
统计与数据挖掘实验学生姓名:学号:学院:经济与管理学院指导老师:专业:日期:2016/1/19数据挖掘——回归分析一.回归分析概述回归分析是一种应用极为广泛的数量分析方法。
它用于分析事物之间的统计关系,侧重考察变量之间的数量变化规律,并通过回归方程的形式描述和反映这种关系,帮助人们准确把握变量受其他一个或多个变量影响的程度,进而为预测提供科学依据。
二.回归分析一般步骤1.确定回归方程中解释变量和被解释变量2.确定回归模型3.建立回归方程4.对回归方程进行各种检验5.利用回归方程进行预测三.回归分析例题为研究高等院校人文社会科学研究中立项课题数受哪些因素的影响,收集某年31个省市自治区部分高校有关社科研究方面的数据,并利用线性回归分析方法进行分析。
这里,被解释变量为立项课题总数,解释变量为投入总人数、投入高级职称的人数、投入科研事业费,专著数,论文数、获奖数。
1.数据结构定义:A 先在spss变量窗口对数据结构进行定义,并相应的定义标签定义结果如下。
B 紧接着在spss数据编辑窗口进行相应的数据录入。
(共31组数据)2.用spss进行回归分析A.选择菜单:分析-回归-线性。
B.选择观测变量到因变量列表和因子框中。
控制变量有几个不同的取值就表示控制变量有几个水平。
C.分析结果如下由于该方程中有多个解释变量,因此,应参考调整系数的判定系数,为0.924,较接近1,因此,认为拟合优度较高,被解释变量可以被模型解释的部分较多,不能被解释的部分较少。
F检验统计量的观测值为61.532,对应的概率P值近似为0.小于显著性水平a,应拒绝回归方程显著性检验的原假设,认为各回归系数不同时为0,被解释变量与解释变量全体的线性关系是显著地,可建立线性模型。
如果显著性水平a为0.05,除投入人数以外,其他变量的回归系数显著性t检验的概率P-值都大于显著性水平a,因此不应拒绝原假设,认为这些偏回归系数与0无显著差异,它们与被解释变量的线性关系是不显著的,不应该保留在方程中。
SPSS对主成分回归实验报告一、实验目的本实验的目的是利用SPSS软件对主成分回归进行分析,通过降维处理建立回归模型,并对模型结果进行解释和评估。
二、实验数据本实验使用的数据为一个假设情景中的模拟数据,包含自变量x1、x2、x3和因变量y。
数据集共有100个样本,样本量较小,主成分回归的效果可以更好地展示。
三、分析方法及步骤1.导入数据首先,在SPSS软件中导入实验数据,并进行必要的数据预处理,例如检查数据的缺失情况和异常值,并进行处理。
2.主成分分析使用PCA方法对自变量进行降维处理。
在SPSS软件中,选择“分析”菜单下的“尺度分析”选项,选择需要进行主成分分析的自变量,并设置合适的选项参数,例如保留主成分的方差解释比例。
3.主成分得分计算利用主成分分析得到的特征值和特征向量信息,对样本数据集进行主成分得分计算,得到降维后的自变量。
4.主成分回归通过主成分得分和因变量之间的回归分析,建立主成分回归模型。
在SPSS软件中,选择“分析”菜单下的“回归”选项,将主成分得分作为自变量,因变量作为被解释变量,进行回归分析。
通过观察回归模型的系数、显著性检验和拟合优度等指标,对主成分回归模型进行评估。
5.结果解释和模型选择根据主成分回归的结果,解释模型中各个主成分的影响程度和对因变量的贡献。
通过模型评估指标和领域知识的综合考虑,选择合适的主成分回归模型。
四、结果分析通过SPSS软件分析主成分回归模型后,得到了以下结果:1.主成分分析的解释方差比为0.785,表示保留的主成分能够解释原始变量78.5%的方差。
2.主成分得分的系数表明,对于因变量y的预测,主成分1和主成分3具有显著正向影响,而主成分2则具有显著负向影响。
3.模型的拟合优度(例如R方)为0.602,说明主成分回归模型可以解释因变量y的60.2%变异。
综合以上结果,我们可以得出结论:在这个假设情景中,使用主成分回归对于因变量y的预测具有一定的效果,但存在一些主成分对因变量y的贡献不显著的情况。
回归分析作业一、利用软件计算1、数据文件“资产评估1”提供了35家上市公司资产评估增值的数据。
num---公司序号pg---- 资产评估增值率gz----固定资产在总资产中所占比例fz----权益与负债比bc----总资产投资报酬率gm---公司资产规模(亿元)a.建立关于资产评估增值率的四元线性回归方程,并通过统计分析、检验说明所得方程的有效性,解释各回归系数的经济含义。
b.剔除gz变量,建立关于资产评估增值率的三元线性回归方程,与a中的模型相比较,那个更为实用有效,说明理由。
解:由Model Summary和ANOVA表可知,R为,决定系数R2为,校正决定系数为。
拟合的回归模型F值为,P值为0,所以拟合的模型是有统计意义的。
从系数的t检验可以看出,只有固定资产比重的sig值=>,说明只有固定资产比重对资产评估增值率的影响是不显著的,其他自变量对固定资产增值的比率均有显著的影响。
线性回归方程为:pg=+++-0.044gmα1=表示,在权益与负债比、总资产投资报酬率和公司规模不变的条件下,固定资产比重每增加1个单位,资产评估增值率增加。
α2=表示,在固定资产比重、总资产投资报酬率和公司规模不变的条件下,权益与负债比每增加1个单位,资产评估增值率增加。
α3=表示,在固定资产比重、权益与负债比和公司规模不变的条件下,总资产投资报酬率每增加1个单位,资产评估增值率增加。
α4=表示,在固定资产比重、权益与负债比和总资产投资报酬率不变的条件下,公司规模每增加1亿元,资产评估增值率减少为。
从系数的t检验可以看出,该模型的回归系数都通过检验。
所以,剔除 gz 变量,建立关于资产评估增值率的三元线性回归方程为:pg=++-0.040gmb更为有效实用,因为所有的回归系数都通过了t检验,并且b模型估计的标准误较小。
2、数据文件“房产销售”提供了20件房地产的销售价格和评估的数据(美元):y----销售价格; x1----地产评估价值; x2----房产评估价值;x3----面积(平方英尺)。
a.建立适当的关于销售价格的多元线性回归模型.b.利用模型预测地产评估价值为2000,房产评估价值为12000,面积为1100的销售价格,并给出预测值的95%的置信区间。
c.通过对模型的统计检验说明预测值的可信度。
解:a.SPSS数据如下由图表所知,地产价值的sig值过高,所以地产价值对销售价格的影响不显著。
把地产价值剔除后,所得的数据如下:由Coefficients表所知,回归方程为:y=++b.解:通常先做enter,然后做逐步(1)对原数据进行回归分析,得到回归方程为:y=++(2)地产评估价值为2000,房产评估价值为12000,面积为1100的销售价格的95%的置信区间为:(,)。
(3)该模型的Adjusted R Square=,也就是这两个自变量可以解释%的因变量变差,应该说是预测的可信度比较高;并且残差符合正态性、独立性和方差齐次性,模型成立,即有95%的可能性b的预测值在区间内。
3、大多数公司都提供了β估计值,以反映证券的系统风险。
一种股票的β值所测量的是这种股票的回报率与整个市场平均回报率之间的关系。
这个指标的名称就来自简单线性回归中的斜率参数β。
在这种回归中,因变量是股票回报率(Y)。
而自变量则是市场回报率(X)。
值大于1的股票被称为“攻击性”证券,因为它们的回报率变动(向上或向下)得比整个市场的回报率快。
相反,β值小于1的股票被称为“防御性”证券,因为它们的回报率变动的比市场回报率慢。
值接近1的股票被称为“中性”证券,因为它们的回报率反映市场回报率。
下面表中的数据是随机抽选的7个月内某只特定的股票的月回报率及整个市场的回报率。
试对这些数据完成简单线性回归分析。
根据你的分析结果,你认为这只股票是属于攻击性,防御性,还是中性解:得到回归方程:y=。
β值为线性回归斜率参数>1,所以,该股票属于“攻击性股票”。
4、参考上题。
股票的β值是否依赖于计算回报率的时间长度因为有些经济商号用的是按月数据计算的β值,另一些经济商号则用按年数据计算的β值,所以这个问题对投资者来说很重要。
H.莱维分别研究了三类股票的时间长度(月)和平均β值。
将时间长度从一个月逐步增加到30个月,莱维计算了年间144只股票的回报率。
根据他所得的β值,这144只股票中有38只攻击性股票,38只防御性股票,以及68只中性股票。
下表中给出的这三类股票对不同时间水平的平均β值。
A、对于攻击性股票、防御性股票和中性股票三种情况,分别求表达平均β值Y与时间长度X之间关系的最小二乘简单线性回归方程。
B、对每一类股票检验假设:时间长度是平均β值的有效线性预测器,检验时用α=。
C、对每一类股票,构造直线斜率的95%置信区间,哪只股票的β值随时间长度的增大而线性增大5个人计算机(PC 机)正以非凡的技术在发展,PC 机的零售价格也是这样。
由于购买时间和机器特点不同,一台PC 机的零售价格可能发生戏剧性的变化。
不久前收集了一批IBM PC 机和IBM PC 兼容机的零售价格数据,共有N=60,见数据文件“计算机价格”。
这些数据被用来拟合多元回归E (Y )=β0+β1 x 1+β2x 2 其中:Y=零售价格(美元)x 1=微处理器速度(兆赫)⎩⎨⎧= 286CPU0 386CPU1芯片芯片Xa 、 试写出最小二乘预测方程。
b 、 此模型是否适合于预测用α=进行检验。
c 、 构造β1 的90%置信区间,并对此区间作出解释。
d 、 本模型中的CPU 芯片(x 2)是否是价格(Y )的有效预测器用α=进行预测。
6、在工厂中,准确估计完成一项作业所需的工时数对于诸如决定雇佣工人的数量,确定向客户报价的最后期限,或者作出与预算有关的成本分析决策等决策管理来说是极端重要的。
一名锅炉筒制造商想预测在一些在未来预测项目中装配锅炉筒所需的工时数。
为了用回归方法实现此目标,他收集了35个锅炉的项目数据(数据文件“锅炉”)。
除工时(Y)外,被测量的变量有锅炉工作容量(X1=磅/小时),锅炉设计压力(X2=磅/平方英寸),锅炉的类型(X3=1,如在生产领域装配;X3=0,如在使用领域装配),以及炉筒类型(X4=1,蒸汽炉筒;X4=0,液体炉筒)。
A、试检验假设:锅炉容量(X1)与工时数(Y)之间有正线性关系。
B、试检验假设:锅炉压力(X3)与工时数(Y)之间有正线性关系。
C、构造β1的95%置信区间并对结果做出解释。
D、构造β3的95%置信区间。
Correlations工时y容量x1工时y Pearson Correlation1.827** Sig. (2-tailed).000N3535容量x1Pearson Correlation.827**1 Sig. (2-tailed).000N3535 **. Correlation is significant at the level (2-tailed).Correlations工时y压力x2工时y Pearson Correlation1.657**Sig. (2-tailed).000N3535压力x2Pearson Correlation.657**1Sig. (2-tailed).000N3535**. Correlation is significant at the level (2-tailed).Coefficients aModel Unstandardized CoefficientsStandardizedCoefficientst Sig.95% Confidence Interval for BB Std. Error Beta Lower Bound Upper Bound1(Constant).005容量x1.009.001.903.000.007.011压力x2.661.388.007.549炉类型x3.531.001筒类型x4.392.000a. Dependent Variable: 工时y7Cushman & Wakefield 股份有限公司,采集了美国市场上办公用房的空闲率和租金率的数据。
对于18个选取的销售地区,这些地区的中心商业区的综合空闲率(%)和平均租金率(美元/平方英尺)的数据(The Wall Journal Almanac1988)见文件“办公用房”。
a.用水平轴表示空闲率,对这些数据画出散点图。
b.这两个变量之间显出什么关系吗c.求出在办公用房的综合空闲率已知时,能用来预测平均租金率的估计的回归方程。
d.在显著水平下检验关系的显著性。
e.估计的回归方程对数据的拟合好吗请解释。
f.在一个综合空闲率是25%的中心商业区,预测该市场的期望租金率。
g.在劳德代尔堡的中心商业区,综合空闲率是%,预测劳德代尔堡的期望租金率。
Correlations综合空闲平均租金综合空闲Pearson Correlation1**Sig. (2-tailed).0038.PJH&D公司正在决定是否为公司新的文字处理系统签订一项维修合同。
公司的管理人员认为,维修费用与该系统的使用时间有关。
采集的每周时间(小时)和面维修费用(千美元)的统计资料见“文字处理系统”。
a.求出年维修费用对于每周使用时间的估计的回归方程。
b.在显著水平下,检验在(a)中求出关系的显著性。
c.PJH&D公司预期每周使用文字处理系统的时间是30小时,求出该公司的年维修费用的95%的预测区间。
d.如果维修合同的费用是每年3000美元,你建议签订这个合同吗,为什么e.f.ANOVA bModel Sum of Squares df Mean Square F Sig.1Regression1.000ag.9.对于一个较大的人口密集的地区,当地交通部门想要确定公共汽车的使用时间和年维修费用之间是否存在某种关系。
由10辆公共汽车组成一个样本,采集的数据见文件“交通”。
a.利用最小二乘法求出估计的回归方程。
b.在 =的显著水平下,通过检验是否看出二变量之间存在一个显著的关系。
c.最小二乘法回归线给出了观测数据一个好的拟合吗请做出解释。
d.如果有一辆特定的公共汽车已使用了4年,求出这辆车年维修费用的一个95%的预测区间。
10.美国心脏协会经过10年的研究,得到了与发生中风有关的年龄、血压和吸烟的统计资料。
假设这一研究的部分数据为文件“中风风险”。
我们将病人在今后10年内发生中风的概率(乘100)看作为中风风险。
我们用一个虚拟变量来定义病人是否为吸烟者,1表示是吸烟者,0表示不是吸烟者。
a.利用这些数据,建立一个中风风险关于个人的年龄、血压和是否吸烟的估计的回归方程。