SPSS 统计分析多元线性回归分析方法操作与及分析

SPSS多元线性回归分析实例操作步骤在数据分析领域，多元线性回归分析是一种强大且常用的工具，它能够帮助我们理解多个自变量与一个因变量之间的线性关系。

接下来，我将为您详细介绍使用 SPSS 进行多元线性回归分析的具体操作步骤。

首先，准备好您的数据。

数据应该以特定的格式整理，通常包括自变量和因变量的列。

确保数据的准确性和完整性，因为这将直接影响分析结果的可靠性。

打开 SPSS 软件，在菜单栏中选择“文件”，然后点击“打开”，找到您存放数据的文件并导入。

在导入数据后，点击“分析”菜单，选择“回归”，再点击“线性”。

这将打开多元线性回归的对话框。

在“线性回归”对话框中，将您的因变量拖放到“因变量”框中，将自变量拖放到“自变量”框中。

接下来，点击“统计”按钮。

在“统计”对话框中，您可以选择一些常用的统计量。

例如，勾选“估计”可以得到回归系数的估计值；勾选“置信区间”可以得到回归系数的置信区间；勾选“模型拟合度”可以评估模型的拟合效果等。

根据您的具体需求选择合适的统计量，然后点击“继续”。

再点击“图”按钮。

在这里，您可以选择生成一些有助于直观理解回归结果的图形。

比如，勾选“正态概率图”可以检查残差的正态性；勾选“残差图”可以观察残差的分布情况等。

选择完毕后点击“继续”。

然后点击“保存”按钮。

您可以选择保存预测值、残差等变量，以便后续进一步分析。

完成上述设置后，点击“确定”按钮，SPSS 将开始进行多元线性回归分析，并输出结果。

结果通常包括多个部分。

首先是模型摘要，它提供了一些关于模型拟合度的指标，如 R 方、调整 R 方等。

R 方表示自变量能够解释因变量变异的比例，越接近 1 说明模型拟合效果越好。

其次是方差分析表，用于检验整个回归模型是否显著。

如果对应的p 值小于给定的显著性水平（通常为 005），则说明模型是显著的。

最重要的是系数表，它给出了每个自变量的回归系数、标准误差、t 值和 p 值。

回归系数表示自变量对因变量的影响程度，p 值用于判断该系数是否显著不为 0。

SPSS 统计分析多元线性回归分析方法操作与分析实验目的：引入1998~2008年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量，来研究上海房价的变动因素。

实验变量：以年份、商品房平均售价（元/平方米）、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。

实验方法：多元线性回归分析法软件：spss19.0操作过程：第一步：导入Excel数据文件1.open data document——open data——open；2. Opening excel data source——OK.第二步：1.在最上面菜单里面选中Analyze——Regression——Linear ，Dependent（因变量）选择商品房平均售价，Independents（自变量）选择城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率、房屋空置率；Method 选择Stepwise.进入如下界面：2.点击右侧Statistics，勾选Regression Coefficients（回归系数）选项组中的Estimates；勾选Residuals（残差）选项组中的Durbin-Watson、Casewise diagnostics默认；接着选择Model fit、Collinearity diagnotics；点击Continue.3.点击右侧Plots，选择*ZPRED（标准化预测值）作为纵轴变量，选择DEPENDNT（因变量）作为横轴变量；勾选选项组中的Standardized Residual Plots（标准化残差图）中的Histogram、Normal probability plot；点击Continue.4.点击右侧Save，勾选Predicted Vaniues（预测值）和Residuals（残差）选项组中的Unstandardized；点击Continue.5.点击右侧Options，默认，点击Continue.6.返回主对话框，单击OK.输出结果分析：1.引入/剔除变量表Variables Entered/Removed aModel Variables Entered Variables Removed Method1 城市人口密度(人/平方公里) . Stepwise (Criteria:Probability-of-F-to-enter<= .050,Probability-of-F-to-remove >=.100).2 城市居民人均可支配收入(元) . Stepwise (Criteria:Probability-of-F-to-enter<= .050,Probability-of-F-to-remove >=.100).a. Dependent Variable: 商品房平均售价（元/平方米）该表显示模型最先引入变量城市人口密度(人/平方公里)，第二个引入模型的是变量城市居民人均可支配收入(元)，没有变量被剔除。

SPSS 统计分析多元线性回归分析方法操作与分析实验目的：引入1998~2008年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量，来研究上海房价的变动因素。

实验变量：以年份、商品房平均售价（元/平方米）、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。

实验方法：多元线性回归分析法软件：spss19.0操作过程：第一步：导入Excel数据文件1.open data document——open data——open；2. Opening excel data source——OK.第二步：1.在最上面菜单里面选中Analyze——Regression——Linear ，Dependent（因变量）选择商品房平均售价，Independents（自变量）选择城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率、房屋空置率；Method 选择Stepwise.进入如下界面：2.点击右侧Statistics，勾选Regression Coefficients（回归系数）选项组中的Estimates；勾选Residuals（残差）选项组中的Durbin-Watson、Casewise diagnostics默认；接着选择Model fit、Collinearity diagnotics；点击Continue.3.点击右侧Plots，选择*ZPRED（标准化预测值）作为纵轴变量，选择DEPENDNT（因变量）作为横轴变量；勾选选项组中的Standardized Residual Plots（标准化残差图）中的Histogram、Normal probability plot；点击Continue.4.点击右侧Save，勾选Predicted Vaniues（预测值）和Residuals（残差）选项组中的Unstandardized；点击Continue.5.点击右侧Options，默认，点击Continue.6.返回主对话框，单击OK.输出结果分析：1.引入/剔除变量表Variables Entered/Removed aModel Variables Entered Variables Removed Method1 城市人口密度(人/平方公里) . Stepwise (Criteria:Probability-of-F-to-enter<= .050,Probability-of-F-to-remove >=.100).2 城市居民人均可支配收入(元) . Stepwise (Criteria:Probability-of-F-to-enter<= .050,Probability-of-F-to-remove >=.100).a. Dependent Variable: 商品房平均售价（元/平方米）该表显示模型最先引入变量城市人口密度(人/平方公里)，第二个引入模型的是变量城市居民人均可支配收入(元)，没有变量被剔除。

spss多元回归分析的报告怎么做：怎么做回归报告分析s pss 多元线性回归spss操作spss回归分析结果解释spss多元线性回归结果篇一：SPSS多元线性回归分析实例操作步骤SPSS 统计分析多元线性回归分析方法操作与分析实验目的：引入1998~2008年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量，来研究上海房价的变动因素。

实验变量：以年份、商品房平均售价（元/平方米）、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。

实验方法：多元线性回归分析法软件：spss19.0操作过程：第一步：导入Excel数据文件1. open data document——open data——open；2. Opening excel data source——OK.第二步：1.在最上面菜单里面选中Analyze——Regression——Linear ，Dependent（因变量）选择商品房平均售价，Independents（自变量）选择城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率、房屋空置率；Method选择Stepwise.进入如下界面：2.点击右侧Statistics，勾选Regression Coefficients（回归系数）选项组中的Estimates；勾选Residuals（残差）选项组中的Durbin-Watson、Casewise diagnostics默认；接着选择Model fit、Collinearity diagnotics；点击Continue.3.点击右侧Plots，选择*ZPRED（标准化预测值）作为纵轴变量，选择DEPENDNT（因变量）作为横轴变量；勾选选项组中的Standardized Residual Plots（标准化残差图）中的Histogram、Normal probability plot；点击Continue.4.点击右侧Save，勾选Predicted Vaniues（预测值）和Residuals （残差）选项组中的Unstandardized；点击Continue.5.点击右侧Options，默认，点击Continue.6.返回主对话框，单击OK.输出结果分析：1.引入/剔除变量表该表显示模型最先引入变量城市人口密度(人/平方公里)，第二个引入模型的是变量(转载于: 写论文网:spss 多元回归分析的报告怎么做)城市居民人均可支配收入(元)，没有变量被剔除。

SPSS多元线性回归分析实例操作步骤多元线性回归是一种常用的统计分析方法，用于探究多个自变量对因变量的影响程度。

SPSS（Statistical Package for the Social Sciences）是一款常用的统计软件，可以进行多元线性回归分析，并提供了简便易用的操作界面。

本文将介绍SPSS中进行多元线性回归分析的实例操作步骤，帮助您快速掌握该分析方法的使用。

步骤一：准备数据在进行多元线性回归分析之前，首先需要准备好相关的数据。

数据应包含一个或多个自变量和一个因变量，以便进行回归分析。

数据可以来自实验、调查或其他来源，但应确保数据的质量和可靠性。

步骤二：导入数据在SPSS软件中，打开或创建一个新的数据集，然后将准备好的数据导入到数据集中。

可以通过导入Excel、CSV等格式的文件或手动输入数据的方式进行数据导入。

确保数据被正确地导入到SPSS中，并正确地显示在数据集的各个变量列中。

步骤三：进行多元线性回归分析在SPSS软件中，通过依次点击"分析"-"回归"-"线性"，打开线性回归分析对话框。

在对话框中，将因变量和自变量移入相应的输入框中。

可以使用鼠标拖拽或双击变量名称来快速进行变量的移动。

步骤四：设置分析选项在线性回归分析对话框中，可以设置一些分析选项，以满足具体的分析需求。

例如，可以选择是否计算标准化回归权重、残差和预测值，并选择是否进行方差分析和共线性统计检验等。

根据需要，适当调整这些选项。

步骤五：获取多元线性回归分析结果点击对话框中的"确定"按钮后，SPSS将自动进行多元线性回归分析，并生成相应的分析结果。

结果包括回归系数、显著性检验、残差统计和模型拟合度等信息，这些信息可以帮助我们理解自变量对因变量的贡献情况和模型的拟合程度。

步骤六：解读多元线性回归分析结果在获取多元线性回归分析结果之后，需要对结果进行解读，以得出准确的结论。

SPSS多元线性回归在医学统计分析中的应用操作及分析之前我们详细讲解了因变量为二分类的变量的影响因素的分析，采用二元Logistic回归分析。

但是在实际情况中，有些因变量的数据类型为连续数值型变量，并无特定的分类，这时候要分析他的影响因素，就无法采用logistics 回归，由于变量数据为线性数值，这里就要采用线性回归模型来分析。

本次我们就来详细讲解SPSS多元线性回归在医学统计分析中的应用操作。

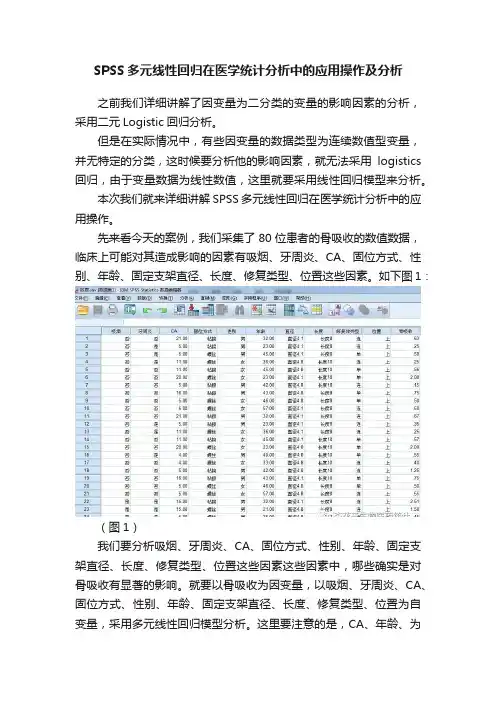
先来看今天的案例，我们采集了80位患者的骨吸收的数值数据，临床上可能对其造成影响的因素有吸烟、牙周炎、CA、固位方式、性别、年龄、固定支架直径、长度、修复类型、位置这些因素。

如下图1：（图1）我们要分析吸烟、牙周炎、CA、固位方式、性别、年龄、固定支架直径、长度、修复类型、位置这些因素这些因素中，哪些确实是对骨吸收有显著的影响。

就要以骨吸收为因变量，以吸烟、牙周炎、CA、固位方式、性别、年龄、固定支架直径、长度、修复类型、位置为自变量，采用多元线性回归模型分析。

这里要注意的是，CA、年龄、为线性变量，可以直接作为自变量，但是吸烟、牙周炎这些属于分类变量，本应先对其进行虚拟化，才能作为自变量，但是由于这里的分类变量全部为二分类，因此虚拟化操作和当前实际一致，因此可直接作为自变量。

关于如何做多分类自变量虚拟化的线性回归，我们将在今后的文章中再另行详解。

下面进行SPSS多元线性回归的操作步骤①点击“分析”--“回归”--“线性”，在弹出的回归对话框中，将骨吸收选入因变量框中，将其他变量选入自变量框中。

（图2）（图3）②进行相关的输出和参数设置，点击右侧“自助抽样”按钮，在弹出的对话框中勾选“执行自助抽样”，“置信区间”级别填写95。

然后点击继续，确定按钮。

（图4）③得到输出结果，并进行分析。

这里我们只对重要的表格进行详细讲解分析。

（图5）模型摘要这张表，主要看R方为52.6%，大于50%，说明数据与模型拟合程度较好。

如何用SPSS进行多元线性回归1、导入数据首先打开SPSS软件，选中打开其他文件，然后把查找范围定位到数据所在位置（我这里是在桌面），然后在文件类型上选择你的文件类型（我这里是Excel），然后选中数据文件，点击打开。

在弹出的对话框中点击确定2、进行描述性统计首先点击菜单栏中的分析-描述统计-描述出现如下页面，选中想要进行描述性统计的变量到右边变量框中。

如图所示，点击选项，选择需要SPSS汇报的描述性统计：结果如图，这里只选择平均值、标准偏差、最小值和最大值：得出描述性统计如图：注意：结果是可以复制粘贴到Excel里面的。

3、相关性分析首先点击菜单栏中的分析-相关-双变量同样按照描述性统计的操作，把想要进行分析的变量选中，选择Pearson相关系数，并进行双尾检验（一般性操作），点击确定即可。

得出如下结果：一般来讲，相关系数大于0.6就说明可能会存在多重共线性问题，而且相关系数比较显著（右上角有两个星号，说明结果在0.01的水平上显著），结论：GYZCZ和SCALE可能存在多重共线性。

4、回归以及回归诊断首先点击分析-回归-线性因变量和自变量选择好，如图所示：点击右上角的Statistics，出现如下菜单，选择共线性诊断和Durbin-Watson检验（检验序列相关性），然后点击继续。

点击右上角的绘图，出现如下界面，按照图示进行选择，这一步是为了进行异方差的初步验证，然后点击继续。

以上全部设定好了之后，点击确定即可。

主要结果分析：可决系数R方值为0.432，调整后的R方是0.414，说明模型拟合程度还不错（一般大于0.3都还能接受）。

D.W.值为0.828，说明存在正的序列相关性（如果是横截面数据，则不需要考虑，如果是时间序列数据就需要考虑用差分法、广义最小二乘、可行的广义最小二乘等方法）F值通过检验（显著性为0.000），说明模型的整体线性性满足。

共线性诊断：看方差膨胀因子（VIF），GYZCZ与SCALE的VIF值大于10，说明存在多重共线性，需要剔除这两个变量。

多元回归分析中的变量选取——SPSS的应用统计学在多元回归分析中，变量选取是一个非常重要的步骤，可以决定模型的准确性和可解释性。

本文将介绍如何使用SPSS进行变量选取，并给出一些常用的变量选取方法。

首先，打开SPSS软件并加载数据集。

然后，在菜单栏中选择“分析”→“回归”→“线性”。

将要分析的依赖变量（因变量）和独立变量（自变量）移动到右边的框中。

点击“方法”选项卡，打开“变量选择”对话框。

SPSS提供了多种变量选取方法，其中一种常用的方法是逐步回归分析。

逐步回归是一种逐渐添加或删除变量的方法，以找到与因变量最相关的自变量组合。

在“变量选择”对话框中，选择“逐步”方法，然后点击“设置”按钮配置选择变量的条件。

逐步回归有两种选择变量的模式：进入模式和删除模式。

进入模式是逐渐从模型中添加自变量，直到没有其他显著的自变量可以添加为止。

删除模式则是一开始将所有自变量添加到模型中，然后逐渐删除非显著的自变量，直到只剩下显著的变量。

在设置条件中，可以选择标准化方法、统计水平以及要使用的模式。

标准化方法有“逐步前向”和“逐步后向”两种选择。

逐步前向是添加变量到模型中，逐渐增加F值，逐步后向则是删除变量，逐渐减小F值。

在统计水平中，可以设置进入模型和离开模型的显著性水平。

通常设置为0.05或0.01点击“确定”后，SPSS将运行逐步回归分析，并显示结果。

结果中将显示模型的显著性、自变量的标准化系数、F值等信息。

在分析的同时，SPSS还会生成一份逐步回归的报告，其中包含了模型的统计指标、显著性检验等内容。

除了逐步回归，SPSS还提供了其他常用的变量选取方法，如逐步逆选择、全部进入、最佳子集等。

每种方法都有其适用的情况，根据具体的研究目的和数据特点选择合适的方法。

值得注意的是，变量选取只是多元回归分析中的一部分，它可以帮助我们找到与因变量最相关的自变量组合，但并不能保证得到最优模型。

因此，在进行变量选取之后，还需要对所选自变量进行进一步的检验和解释，以确保所建立的模型具有合理性和可解释性。

spss多元线性回归分析结果解读SPSS多元线性回归分析结果解读1. 引言多元线性回归分析是一种常用的统计分析方法，用于研究多个自变量对因变量的影响程度及相关性。

SPSS是一个强大的统计分析软件，可以进行多元线性回归分析并提供详细的结果解读。

本文将通过解读SPSS多元线性回归分析结果，帮助读者理解分析结果并做出合理的判断。

2. 数据收集与变量说明在进行多元线性回归分析之前，首先需要收集所需的数据，并明确变量的含义。

例如，假设我们正在研究学生的考试成绩与他们的学习时间、家庭背景、社会经济地位等因素之间的关系。

收集到的数据包括每个学生的考试成绩作为因变量，以及学习时间、家庭背景、社会经济地位等作为自变量。

变量说明应当明确每个变量的测量方式和含义。

3. 描述性统计分析在进行多元线性回归分析之前，我们可以首先对数据进行描述性统计分析，以了解各个变量的分布情况。

SPSS提供了丰富的描述性统计方法，如均值、标准差、最小值、最大值等。

通过描述性统计分析，我们可以获得每个变量的分布情况，如平均值、方差等。

4. 相关性分析多元线性回归的前提是自变量和因变量之间存在一定的相关性。

因此，在进行回归分析之前，通常需要进行相关性分析来验证自变量和因变量之间的关系。

SPSS提供了相关性分析的功能，我们可以得到每对变量之间的相关系数以及其显著性水平。

5. 多元线性回归模型完成了描述性统计分析和相关性分析后，我们可以构建多元线性回归模型。

SPSS提供了简单易用的界面，我们只需要选择因变量和自变量，然后点击进行回归分析。

在SPSS中，我们可以选择不同的回归方法，如逐步回归、前向回归、后向回归等。

6. 回归结果解读在进行多元线性回归分析后，SPSS将提供详细的回归结果。

我们可以看到每个自变量的系数、标准误差、t值、显著性水平等指标。

系数表示自变量与因变量之间的关系程度，标准误差表示估计系数的不确定性，t值表示系数的显著性，显著性水平则表示系数是否显著。

多元线性回归是一种用于描述一个或多个变量(自变量)之间关系的统计学方法。

多元线性回归可以用来预测或估计一个自变量（也称为解释变量）的值，基于一组其他的自变量（也称为预测变量）的值。

SPSS是一款专业的统计分析软件，可以用来进行多元线性回归分析。

使用SPSS进行多元线性回归的步骤如下：
1.准备数据：在SPSS中，你需要准备待分析的数据，包括自变量和因变量。

2.执行回归分析：在SPSS中，可以使用“分析”菜单中的“回归”选项，在此菜单中选择“多元线性回归”，并确定自变量和因变量。

3.分析结果：多元线性回归的结果将会显示在一个表格中，包括拟合参数，R方值，F 检验等。

通过对这些结果的分析，可以了解自变量对因变量的影响程度。

4.模型检验：SPSS也可以用于检验多元线性回归模型的合理性，包括残差分析、多重共线性检验、异方差性检验等。

多元线性回归分析是一项重要的数据分析技术，SPSS是一款功能强大的统计分析软件，提供了多元线性回归分析的完整功能，可以帮助研究者更好地探索数据的内在规律，从而更好地理解和把握数据的特点。

3 利用SPSS10.0进行多元线性回归分析【例】同上例。

第一步，录入或调入数据。

完全类同于一元线性回归分析，不赘述（图1）。

图1 录入或调入的数据第二步，回归操作。

多元线性分析的详细步骤的基本进程与一元线性回归分析相似，稍有不同。

⑴打开线性回归对话框。

即沿着主菜单的Analyse→Regression→Linear…路径打开Linear Regression选项框（图2）。

⑵将“运输业产值”置于因变量（Dependent）的空白栏，将“工业产值”、“农业产值”和“固定资产投资”置于自变量（Independent(s)）的空白栏（图3）。

⑶在统计（Statistics）选项框中，除了选择“Durbin-Watson”外，还应该选择“Part and partial correlations”(部分与偏相关，给出零阶相关系数、偏相关系数和部分相关系数)以及“Collinearity diagnostics（共线性诊断）”。

然后继续。

⑷在Plot选项框中，除了可以选择“Histogram”（直方图）和“Normal probability plot”(正态概率图)外，还可选择“Produce all partial plot(s)”（给出所有自变量与因变量的残差散点图）。

然后继续。

⑸修改显著性水平或置信度，可以进入Save对话框，改变Prediction intervals的Confidence intervals（置信区间）；修改逐步回归的F临界值，可以进入Option选项框，改变Stepping method criteria中的F值或者F概率。

如果对此缺乏足够的知识，可由系统默认。

然后继续。

⑹在线性回归对话框中，Method一栏由系统默认为enter（让所有的自变量都参入回归）。

完成上述设置以后，点击“OK”确定（图3），立即可以得到回归结果（Output）。

图2 线性回归对话框图3 设置变量图4 统计选项框的设置图5 图形对话框的设置在Variables Entered/Removed （变量取舍即变量的输入或剔除）表中，给出的采用的变量、剔除的变量和回归方法（enter ）,此表中没有剔除变量。

如何使用SPSS进行多元统计分析第一章：SPSS简介SPSS（Statistical Package for the Social Sciences）是一种功能强大且广泛使用的统计分析软件。

它能够处理大量数据，进行各种统计分析和数据挖掘，是研究人员和数据分析师常用的工具。

第二章：设置数据在进行多元统计分析之前，首先需要设置数据。

SPSS支持导入外部数据文件，如Excel、CSV等格式。

用户可以在SPSS中创建新的数据集并录入数据，也可以导入已有数据集。

在设置数据时，需要注意数据的变量类型、缺失值处理以及数据的清洗与转换。

第三章：描述统计分析描述统计分析是理解数据的第一步。

SPSS提供了丰富的描述统计方法，包括平均数、标准差、最小值、最大值、频数分布等。

用户可以通过简单的命令或者界面操作来生成各种描述统计结果，并进一步进行数据的可视化展示。

第四章：相关性分析相关性分析是多元统计分析的常用方法之一。

SPSS提供了丰富的相关性分析工具，如Pearson相关系数、Spearman等。

用户可以通过相关分析来检测不同变量之间的关系，并进一步探索变量之间的线性或非线性关系。

第五章：线性回归分析线性回归分析是一种预测性分析方法，在多元统计分析中应用广泛。

SPSS可以进行简单线性回归分析和多元线性回归分析。

用户可以通过线性回归分析来建立模型，预测因变量与自变量之间的关系，并进行参数估计和显著性检验。

第六章：因子分析因子分析是一种常用的降维技术，用于发现隐藏在数据中的潜在变量。

SPSS提供了主成分分析、最大似然因子分析等方法。

用户可以通过因子分析来降低变量的维度，提取数据中的主要信息。

第七章：聚类分析聚类分析是一种用于将数据样本划分成相似组的方法。

SPSS支持多种聚类算法，如K均值聚类、层次聚类等。

用户可以通过聚类分析来识别数据中的固有模式和群体。

第八章：判别分析判别分析是一种用于将样本分类的方法，常用于研究预测变量对分类变量的影响。

SPSS 统计分析多元线性回归分析方法操作与分析实验目的：引入1998~2008年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量，来研究上海房价的变动因素。

实验变量：以年份、商品房平均售价（元/平方米）、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。

实验方法：多元线性回归分析法软件：操作过程：第一步：导入Excel数据文件1.open data document——open data——open；2. Opening excel data source——OK.第二步：1.在最上面菜单里面选中Analyze——Regression——Linear ，Dependent（因变量）选择商品房平均售价，Independents（自变量）选择城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率、房屋空置率；Method选择Stepwise.进入如下界面：2.点击右侧Statistics，勾选Regression Coefficients（回归系数）选项组中的Estimates；勾选Residuals（残差）选项组中的Durbin-Watson、Casewise diagnostics默认；接着选择Model fit、Collinearity diagnotics；点击Continue.3.点击右侧Plots，选择*ZPRED（标准化预测值）作为纵轴变量，选择DEPENDNT（因变量）作为横轴变量；勾选选项组中的Standardized Residual Plots（标准化残差图）中的Histogram、Normal probability plot；点击Continue.4.点击右侧Save，勾选Predicted Vaniues（预测值）和Residuals（残差）选项组中的Unstandardized；点击Continue.5.点击右侧Options，默认，点击Continue.6.返回主对话框，单击OK.输出结果分析： 1.引入/剔除变量表该表显示模型最先引入变量城市人口密度 (人/平方公里)，第二个引Variables Entered/Removed aModel Variables Entered Variables RemovedMethod1城市人口密度 (人/平方公里). Stepwise (Criteria: Probability-of-F-to-enter <= .050,Probability-of-F-to-remove >= .100).2城市居民人均可支配收入(元). Stepwise (Criteria: Probability-of-F-to-enter <= .050,Probability-of-F-to-remove >= .100).a. Dependent Variable: 商品房平均售价（元/平方米）入模型的是变量城市居民人均可支配收入(元)，没有变量被剔除。

SPSS多元线性回归分析报告实例操作步骤步骤1：导入数据首先，打开SPSS软件，并导入准备进行多元线性回归分析的数据集。

在菜单栏中选择"File"，然后选择"Open"，在弹出的窗口中选择数据集的位置并点击"Open"按钮。

步骤2：选择变量在SPSS的数据视图中，选择需要用于分析的相关自变量和因变量。

选中的变量将会显示在变量视图中。

确保选择的变量是数值型的，因为多元线性回归只适用于数值型变量。

步骤3：进行多元线性回归分析在菜单栏中选择"Analyze"，然后选择"Regression"，再选择"Linear"。

这将打开多元线性回归的对话框。

将因变量移动到"Dependent"框中，将自变量移动到"Independent(s)"框中，并点击"OK"按钮。

步骤4：检查多元线性回归的假设在多元线性回归的结果中，需要检查多元线性回归的基本假设。

这些假设包括线性关系、多重共线性、正态分布、独立性和等方差性。

可以通过多元线性回归的结果来进行检查。

步骤5：解读多元线性回归结果多元线性回归的结果会显示在输出窗口的回归系数表中。

可以检查各个自变量的回归系数、标准误差、显著性水平和置信区间。

同时，还可以检查回归模型的显著性和解释力。

步骤6：完成多元线性回归分析报告根据多元线性回归的结果，可以编写一份完整的多元线性回归分析报告。

报告应包括简要介绍、研究问题、分析方法、回归模型的假设、回归结果的解释以及进一步分析的建议等。

下面是一个多元线性回归分析报告的示例：标题：多元线性回归分析报告介绍：本报告基于一份数据集，旨在探究x1、x2和x3对y的影响。

通过多元线性回归分析，我们可以确定各个自变量对因变量的贡献程度，并检验模型的显著性和准确性。

研究问题：本研究旨在探究x1、x2和x3对y的影响。

只有一个自变量和因变量的线性回归称为简单线性回归，但是实际上，这样单纯的关系在现实世界中几乎不存在，万事万物都是互相联系的，一个问题的产生必定多种因素共同作用的结果。

对于有多个自变量和一个因变量的线性回归称为多重线性回归，有的资料上称为多元线性回归，但我认为多元的意思应该是真的因变量而非自变量的，而且多重共线性这个说法，也是针对多个自变量产生的，因此我还是赞同叫做多重线性回归。

多重线性回归是适用条件和简单线性回归类似，也是自变量与因变量之间存在线性关系、残差相互独立、残差方差齐性，残差呈正态分布，但是由于自变量多于1个，因此还需要要求自变量之间不存在相关性，即不存在多重共线性，但是完全不存在相关的两个变量是不存在的，因此条件放宽为只要不是强相关性，都可以接受。

多重线性回归在SPSS中的操作过程和简单线性回归一样，只是设置的内容多了一些，并且由于考察的信息较多，建议设定分析步骤，常用的步骤为1. 绘制散点图，判断是否存在线性趋势2. 初步建模，包括设定变量筛选方法3. 残差分析，分析建模之后的残差的正态性，独立性，方差齐性等问题4. 强影响点和多重共线性的判断5. 根据以上分析结果修正模型，并重复3-4，直到模型达到最优效果分析一回归一线性本例研究的是猪的痩肉呈和三个部程肉最的关系.因变量只能选入一个，而自变量可U納入多个，在自变量选择上，根据专业经验"a 们认为这些自喪量都比校重要*因哉吏最的筛选方法选择向启法V Dur^rbWatson(U)區个務羽斷9)© X^tf (o )： [3[标爪丧在毓计量按钮中，除了 默认的估计和模型拟合 度之外.我们再选择共 线性诊断、Durbin.- Tatsom 个案诊断・这 三个的作用分别是，判 断共线性、栓查残差的 独立性以及强影响点的 判断在绘制按钮中•主要是输岀残差的统 ifS ＞我们迭择直方團和正态談率 S ＞也可以根据左侧的统计量绘制散 点图•左侧统计童依次为， DEPEHDHT ：因变量•ZPRED:标准化荻测值 ♦ZRESID:标准化残差 •DRESID:ft 除的残差•ADJPREDziS 整的残差 •SRESID: Student •SDRVSID: Student* 除残差 本例我幻在X 轴选择标准化预测值.T 轴选择标准化残差.并选择标准化残 差的直方图和正态談率囲II7 E ・X>A>・HaQWS：♦IP! 1 wn (j )■・■ w 押n £ ®>M»3Wfc —w. ct<rPM>・B^OeB«004N ■ ■ Mfti )<rwa1^ or*r>VMMCCMofFitcr 》W) ・■(*m«CCM<£)■保存按钮用来将一些分 析结果保存在数据中， 以便后续分析，在此我 们不做选择/復SWU 含度廻) 臼負方實化®ElHfc®性SW 相关和■«关也兰Ji 取廨 UV )[</在等式中包含當运（!）@茨列表从稼个案（丄）0按时携降个案®卫便用均値替横（旦）[址缤]取消 ttro结果中，首先看到筛选 变量摘要.因为我们选 择的是向后筛选法，首 先将所有变量纳入模型 中.结果中首先显示转 入三个变量.其次可以 看到.最终将肌肉面积 这个变量移除了.因为 它超过了我们设定的概 率值不链大于0. 1的范 S具次嘗岀的结果是模型孔忌.町以看 出有两个模型，-个是三个变莹全部 迭入时的模型，一个是期除肌肉面枳 变量后的模型，可见，剔除该变量之 后.R 方有所降低，世是调整R 方増 大.说明則除之后的模聖比之前的晏 奸，而且标准误差也有所降低.D-■检 验值在0-4ZfS]>说明残差独立性良好选择按钮用来设置变量 筛选的条件，以及是否 在模型中包含常量，并 且可以对缺失值进行处 理.在此我们选择默认 即可输入的雯量 移上的隹 方法 1 2II 肉量■肌由茴 积供向量b •肌肉面积输入向后（准则:F-to-remove >=.100叭僭 主）msjR R 方 仪”方 •：・e古.rDurbin- Watson1917- &41 $19 462492.>ie b$38$24・45创12 358[挣进方法标慮©）使用F 的韵率Q ） 近丙:]05 瞒邂）| io I ◎便用F«（V ）输入/诈夫的娈量Wa 因変量坡肉量 b.已输入所育诸求B 丁至b 廉ifflg 他(*i). Fol Vnl-aB ScAtwwaa BC ensb t n (京②.审 n®«i iFna e F ；哄=(煮IBn® VHft 模型的整体方差检验显 示，两个模型均有统计 学童义，井且回归部分 的数值也相差不大模型系致表显示，M 肉面积这个变童没有 统计学意义.将其期 除之后，其余变量的 系数值并未发生巨大 变牝，后续的容差和 ▼IF 值为共线性统计 量，容差越接近th K ▼IF 值越接近5,说明 共线性越严重.从本 例情况来看■问題不 大后续的结果也是共线性的诊断，从特 征值指标耒看.除了笫一维之外.其 余的均比较接近.而第一维作为笫一 个主成分，值很大时正當的。

SPSS多元线性回归分析实例操作步骤SPSS（Statistical Package for the Social Sciences）是一种统计分析软件，广泛应用于社会科学研究领域。

其中，多元线性回归分析是SPSS中常用的一种统计方法，用于探讨多个自变量与一个因变量之间的关系。

本文将演示SPSS中进行多元线性回归分析的操作步骤，帮助读者了解和掌握该方法。

一、数据准备在进行多元线性回归分析之前，首先需要准备好数据。

数据应包含一个或多个因变量和多个自变量，以及相应的观测值。

这些数据可以通过调查问卷、实验设计、观察等方式获得。

确保数据的准确性和完整性对于获得可靠的分析结果至关重要。

二、打开SPSS软件并导入数据1. 启动SPSS软件，点击菜单栏中的“文件（File）”选项；2. 在下拉菜单中选择“打开（Open）”选项；3. 导航到保存数据的文件位置，并选择要导入的数据文件；4. 确保所选的文件类型与数据文件的格式相匹配，点击“打开”按钮；5. 数据文件将被导入到SPSS软件中，显示在数据编辑器窗口中。

三、创建多元线性回归模型1. 点击菜单栏中的“分析（Analyse）”选项；2. 在下拉菜单中选择“回归（Regression）”选项；3. 在弹出的子菜单中选择“线性（Linear）”选项；4. 在“因变量”框中，选中要作为因变量的变量；5. 在“自变量”框中，选中要作为自变量的变量；6. 点击“添加（Add）”按钮，将自变量添加到回归模型中；7. 可以通过“移除（Remove）”按钮来删除已添加的自变量；8. 点击“确定（OK）”按钮，创建多元线性回归模型。

四、进行多元线性回归分析1. 多元线性回归模型创建完成后，SPSS将自动进行回归分析并生成结果；2. 回归结果将显示在“回归系数”、“模型总结”和“模型拟合优度”等不同的输出表中；3. “回归系数”表显示各个自变量的回归系数、标准误差、显著性水平等信息；4. “模型总结”表提供模型中方程的相关统计信息，包括R方值、F 统计量等；5. “模型拟合优度”表显示模型的拟合优度指标，如调整后R方、残差平方和等；6. 可以通过菜单栏中的“图形（Graphs）”选项，绘制回归模型的拟合曲线图、残差图等。

spss多重线性回归逐步回归法操作和结果解释方法∙∙|∙浏览：16524∙|∙更新：2012-11-24 22:30∙1∙2∙3∙4∙5∙6∙7分步阅读一键约师傅百度师傅最快的到家服务，最优质的电脑清灰！spss经常用到的一个回归方法是stepwise，也就是逐步回归，它指的是每次只纳入或者移除一个变量进入模型，这个方法虽然好用，但是最后可能出现几个模型都比较合适，你就要比较这几个模型的优劣，这是个麻烦事，这里就给大家简单的分析分析。

方法/步骤1.打开spss以后，打开数据，这些都准备好了以后，我们开始拟合方程，在菜单栏上执行：analyze---regression---linear，打开回归拟合对话框2.在这里，我们将因变量放大dependent栏，将自变量都放到independent栏3.将method设置为stepwise，这就是逐步回归法4.点击ok按钮，开始输出拟合结果5.我们看到的第一个表格是变量进入和移除的情况，因为这个模型拟合的比较好，所以我们看变量只有进入没有移除，但大部分的时候变量是有进有出的，在移除的变量这一栏也应该有变量的6.第二个表格是模型的概况，我们看到下图中标出来的四个参数，分别是负相关系数、决定系数、校正决定系数、随机误差的估计值，这些值（除了随机误差的估计值）都是越大表明模型的效果越好，根据比较，第四个模型应该是最好的7.方差分析表，四个模型都给出了方差分析的结果，这个表格可以检验是否所有偏回归系数全为0，sig值小于0.05可以证明模型的偏回归系数至少有一个不为零8.参数的检验，这个表格给出了对偏回归系数和标准偏回归系数的检验，偏回归系数用于不同模型的比较，标准偏回归系数用于同一个模型的不同系数的检验，其值越大表明对因变量的影响越大。

END经验内容仅供参考，如果您需解决具体问题(尤其法律、医学等领域)，建议您详细咨询相关领域专业人士。

作者声明：本篇经验系本人依照真实经历原创，未经许可，谢绝转载。