当前位置：文档之家 › 高等代数教案张禾瑞版

高等代数教案张禾瑞版

  • 格式：docx
  • 大小：28.03 KB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

高等代数(张禾瑞版)教案-第4章线性方程组

高等代数(张禾瑞版)教案-第4章线性方程组

第四章 线 性 方 程 组4.1 消元法教学目的：1、掌握线性方程组的和等变换，矩阵的初等变换等概念。

理解线性方程组的和等变换是同解变换，以及线性方程组的初等变换可用增广矩阵的相应的行初等变换代替。

2、熟练地掌握用消元发解线性方程组，以及判断线性方程组有没有解和解的个数。

设方程组:a 11x 1+a 12x 2+…+a 1n x n =b 1; a 21x 1+a 22x 2+…+a 2n x n =b 2; (1) ……………………………… a m1x 1+a m2x 2+…+a mn x n =b m . 1 线性方程组的初等变换: 例1解线性方程组:21 x 1 +31x 2 + x 3=1 (2) x 1+ 35x 2 +3 x 3=32x 1+34x 2+5 x 3=2从第一和第三方程分别减去第二个方程的21倍和2倍,来消去前两个方程中的未知量x 1(即把x 1的系数化为零).我们得到:-21 x 1 -21 x 3= -21 x 1+ 35x 2+3 x 3=3-2 x 2- x 3=-4为了计算的方便,我们把第一个方程乘以-2后,与第二个方程交换,得:x1+35x 2+3x 3= 3 x 2+ x 3= 1 -2x 2- x 3=-4把第二个方程的2倍加到第三个方程,来消去后一方程中的未知量x 2,我们得到:x 1+35x 2+3x 3= 3 x 2+ x 3= 1x 3=-2现在很容易求出方程组的解.从第一个方程减去第三个方程的3倍,再从第二个方程减去第三个方程(相当于把x 3的值-2代入第一和第二个方程),得x 1+35x 2=9 x 2=3 x 3=-2再从第一个方程减去第二个方程的35倍(相当于把x 2的值3代入第一个方程),得 x 1=4x 2=3 x 3=-2这样我们就求出了方程组(2)的解.分析一下以上的例子,我们看到,我们对方程组施行了三种变换: 1) 交换两个方程的位置;2) 用一个不等于零的数乘某一个方程; 3) 用一个数乘某一个方程后加到另一个方程. 我们把这三种变换叫做线性方程组的初等变换. 由初等代数知道,以下定理成立.定理4.1.1 初等变换把一个线性方程组边为一个与它同解的线性方程组. 2 矩阵： 利用线性方程组(1)的系数可以排成如下的一个表:(3) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛a aa aa a a a a mn m m n n............ (2)12222111211, 而利用(1)的系数和常数项又可以排成下表:(4) ⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛b aaa b a a b a a a b a a a m mnm m nn ............... (2)133231222221111211.定义1 由st 个数c ij 排成一个s 行t 列的表⎪⎪⎪⎪⎪⎭⎫⎝⎛c c c cc c c c c st s s t t212222111211叫作一个s 行t 列（或s ⨯t ）矩阵。

高等代数电子教案

高等代数电子教案

定理2.6.4 设f (x)与g (x)是R [x]的两个多项式,它们的次数都 不大于n.若是以R中n + 1个或更多的不同的数来代 替x时,每次所得f (x)与g (x)的值都相等,那么 f (x) = g (x) . 证 令 u (x) = f (x) – g (x) 若f (x)≠g (x), 换一句话说, u (x) ≠0 ,那么u (x)是一个 次数不超过n的多项式,并且R中有n + 1个或更多的 根. 这与定理2.6.3矛盾.
当x = c时f (x)的值 f (c) .
综合除法
设f ( x) a0 x n a1 x n 1 a 2 x n 2 a n 1 x a n , 并且设
(1) 其中
f ( x) ( x c) q ( x) r ,
q( x)b x
0 n 1
.... bn 1
f ( x) a0 a1 x ai x a m x , j n g ( x) b0 b1 x b j x bn x ,
i m
c0 , c1 ,cm n .
由于f (x)和g (x)都是本原多项式,所以p不能整除f (x)
的所有系数,也不能整除g (x)的所有系数.令 ai 和b j各
这样,欲求系数 bk ,只要把前一系数 bk 1 乘以c再加 上对应系数 a k ,而余式的 r 也可以按照类似的规律 求出. 因此按照下所指出的算法就可以很快地陆续 求出商式的系数和余式:
c | a0 b0
a1 cb0 b1
a 2 a n 1 cb1 cbn 2 b2 bn r
比较等式(1)中两端同次项的系数,我们得到
a 0 b0 , a1 b1 cb0 , a 2 b2 cb1 , a n 1 bn 1 cbn 2 , a n r cbn 1 .

高等代数教案设计(张禾瑞版)

高等代数教案设计(张禾瑞版)
教学方法
1.讲授法。2.讨论法。3.讲练结合
教学内容及
时间安排
§1 一元多项式的定义和运算2学时
§2 多项式的整除性4学时
习题课 2学时
§3 多项式的最大公因式2学时
§4 多项式的分解2学时
习题课 2学时
§5 重因式2学时
§6 多项多函数，多项式的根2学时
习题课 2学时
§7 复数和实数域上多项式2学时
§4 整数的一些整除性质2学时
§5 数环和数域2学时
习题课 2学时
学习指导
1.复习教材和笔记中本章内容。
2.让学生阅读北京师范大学，高等代数 第一章
3.让学生阅读《高等代数辅助教材》 第一章。
作业及思考题
教材第一章习题：第6页：6、7； 第14页：5、10；第18页：1、4、5；
第29页：2、4、5；第25页：3、5。
§8 有理数域上多项式4学时
习题课 2学时
学习指导
1.复习教材和笔记中本章内容。
2.让学生阅读北京师范大学，高等代数 第二章
3.让学生阅读《高等代数辅助教材》 第二章。
作业及思考题
教材第二章复习思考题：第31页：3 ；第38页：5、6、7；第48页：6、7、9、10、11 ；第56页：3、5、6；第59页：3、4、5 ；第65页：4、7、8；第71页：2、3、4、5； 第80页：2、3、4。
教学难点
矩阵运算及运算规则、矩阵可逆条件及求逆矩阵的方法，求矩阵的秩。初等变换与初等矩阵的关系，矩阵乘积的秩和矩阵乘积的行列式。
教学方法
1.讲授法。2.讨论法。3.讲练结合
教学内容及
时间安排
§1 矩阵的运算2学时
习题课 2学时
§2 可逆矩阵，矩阵乘积的行列式4学时

高等代数电子教案(Ⅲ)

高等代数电子教案(Ⅲ)

进一步，设 f ( x) a0 a1 x an x . 是F上一个多项式，而 L(V ), 以σ代替x，以 a 0 代替 a 0 ，得到V的一个线性变换
n
a0 a1 an n .
这个线性变换叫做当 记作 f ( ).
x 时f (x)的值，并且
7.4 不变子空间 7.5 本征值和本征向量 7.6 可以对角化矩阵
7.1 线性映射
学习内容 线性映射的定义、线性变换的象与核.
§7.1.1 线性映射的定义
设F是一个数域，V和W是F上向量空间. 定义1 设σ是V 到W 的一个映射. 如果下列条 件被满足，就称σ是V 到W 的一个线性映射： ①对于任意 , V , ( ) ( ) ( ). ②对于任意 a F , V , (a ) a ( ) 容易证明上面的两个条件等价于下面一个条件： ③对于任意 a, b F 和任意 , V ,

设 L(v), σ的负变换－σ指的是V到V的映射 : ( ). 容易验证，－σ也是V的线性变换，并且 （4） ( )
线性变换的数乘满足下列算律：
(5) (6) (7) (8)
k ( ) k k , (k l ) k l , (kl) k (l ), 1 ,
f x 与它对应，根据导数的基本性质，这样定义 的映射是F[x]到自身的一个线性映射.
例8 令C[a, b]是定义在[a, b]上一切连续实函数所
成的R上向量空间，对于每一 f x Ca,b, 规定
f x 仍是[a, b]上一个连续实函数，根据积分的
基本性质，σ是C[a, b]到自身的一个线性映射.

高等代数电子教案(Ⅲ)

高等代数电子教案(Ⅲ)
7.4 不变子空间 7.5 本征值和本征向量 7.6 可以对角化矩阵
7.1 线性映射
学习内容 线性映射的定义、线性变换的象与核.
§7.1.1 线性映射的定义
设F是一个数域，V和W是F上向量空间. 定义1 设σ是V 到W 的一个映射. 如果下列条 件被满足，就称σ是V 到W 的一个线性映射： ①对于任意 , V , ( ) ( ) ( ). ②对于任意 a F , V , (a ) a ( ) 容易证明上面的两个条件等价于下面一个条件： ③对于任意 a, b F 和任意 , V ,
进一步，设 f ( x) a0 a1 x an x . 是F上一个多项式，而 L(V ), 以σ代替x，以 a 0 代替 a 0 ，得到V的一个线性变换
n
a0 a1 an n .
这个线性变换叫做当 记作 f ( ).
x 时f (x)的值，并且
例3 令A是数域F上一个m × n矩阵，对于n元列空 间的 F m 每一向量
x1 x2 x n
规定： 是一个m×1矩阵，即是空间 F m的一个向量， σ是 到 F n 的一个线性映射. Fm
例4 令V 和W是数域F 上向量空间.对于V 的每一向 量ξ令W 的零向量0与它对应，容易看出这是V 到 W的一个线性映射，叫做零映射.
令 k ，那么对于任意 a, b F 和任意 , V ,
(a b ) k ( (a b )) k (a ( ) b ( ))
ak ( ) bk ( ) a 的一个线性变换.
如果线性映射 : V W 有逆映射 1 ，那么是W 到V 的一个线性映射. 建议同学给出证明.

高等代数教案

高等代数教案

高等代数教案 The pony was revised in January 2021
高等代数
教案
秦文钊
一、章（节、目）授课计划第页
二、课时教学内容第页
二、课时教学内容第页
一、章（节、目）授课计划第页
二、课时教学内容第页
一、章（节、目）授课计划第页
二、课时教学内容第页
二、课时教学内容第页
二、课时教学内容第页
一、章（节、目）授课计划第页
二、课时教学内容第页
二、课时教学内容第页
一、章（节、目）授课计划第页
二、课时教学内容第页
二、课时教学内容第页
二、课时教学内容第页
一、章（节、目）授课计划第页
二、课时教学内容第页
二、课时教学内容第页
a的代数余子式.称为元素
ij
二、课时教学内容第页
二、课时教学内容第页
一、章（节、目）授课计划第页
二、课时教学内容第页
二、课时教学内容第页
一、章（节、目）授课计划第页
二、课时教学内容第页
二、课时教学内容第页。

高等代数教案(张禾瑞版)

第29页：2、4、5；第25页：3、5。
教研室审阅意见
同意上述安排。
教研室主任签字：王书琴
2005年2月28日
高等代数教案第二章首页
授课内容
第二章多项式
第2．1节——第2。8节
所需课时
28学时
主要教材或
参考资料
1．北京师范大学高等代数高等教育出版社，1997
2．北京大学编高等代数高等教育出版社，1995
知识目标：教学目的和教学基本要求：
（1）掌握集合，子集，空集等基本概念，明确集合、
子集合之间的关系及表示方法。
（2） 掌握映射、单射、满射及双射的基本概念。
（3） 掌握数学归纳原理、最小数原理，第二数学归纳法原理应用。
（4） 掌握带余除法，最大公因数，互素概念和方法。
（5） 掌握数环，数域及最小数域—有理数域为基本概念。
教学目标
知识目标：教学目的和教学基本要求：
（1）掌握排列、n阶行列式的定义和基本性质
（2）掌握子式、余子式、代数余子式及行列式的依行依列展开，克拉默定理。
（3）熟练掌握用化上三角形式，依行依列展开法，以及用行列式性质，建立递推公式，克拉默定理等方法计算行列式，证明行列式的性质及基本理论。
能力目标：（1）训练学生领会和把握n阶行列式的定义和基本性质。
（2）掌握n阶行列式的基本理论、性质，并且能应用这些理论进行n阶行列式的计算以及论证问题。
教学重点
n阶行列式的定义和基本性质、行列式的依行依列展开、克拉默定理、
熟练掌握用化上三角形式、依行依列展开法、以及用行列性质、范德蒙
行列式等方法计算行列式，证明行列式的性质及基本理论。
教学难点
子式、余子式、代数余子式及行列式的依行依列展开、克拉默定理应用、

高等代数(高教版张禾瑞著)课件ppt版(9章)

本章节主要讨论了二次型及其相关概念。首先引入了二次型的定义，即数域F上的n元二次齐次多项式，并阐述了其与对称矩阵的关系。接着，详细探讨了线性变换对二次型的影响，通过变量的线性变换可以得到一个新的二次型，并指出了线性变换矩阵P的重要性。进一，引入了矩阵的合同概念，阐述了合同关系的自反性、对称性和传递性，并指出合同的矩阵具有相同的秩，且与一个对称矩阵合同的矩阵仍是对称的。这些内容为后续深入理解和应用二次型及其相关理论打下了坚实的基础。

《高等代数》教学大纲

《高等代数》课程教学大纲课程类型：专业基础课适用对象：数学教育专业专科生总学时：216学时先修课程：数学分析、空间解析几何等参考书目：1．张禾瑞，郝炳新编，高等代数（M），北京：高等教育出版社，2007年5月。

2．丘维声编，高等代数（M），北京：高等教育出版社，1996年12月。

3. 陈志杰主编，高等代数与解析几何（M）（上下），北京：高等教育出版社、Springer出版社，2000年6月。

4．孟道骥著，高等代数与解析几何（M）（上下），北京: 科学出版社, 1998年。

一、课程的教学目的与任务本课程的教学目的是让学生在掌握一元多项式和线性代数的基础知识、基本理论和基本技能的基础上，初步熟悉和掌握抽象的、严格的代数方法，理解具体与抽象、特殊与一般、有限与无限的辩证关系，提高抽象思维、逻辑推理、分析问题和解决问题的能力。

通过本课程的学习使学生了解和掌握现代数学研究的基本特征和思想方法，培养和提高其抽象思维，推理论证及独立创造的能力。

二、课程的基本要求1．掌握一元多项式理论，并能够深刻把握因式分解与求解的关系；2．熟练掌握矩阵的运算，并能够认识到它的等价分类；3. 充分理解借助线性空间刻画的线性变换的意义，并能够借助不变子空间的直和分解，掌握矩阵的相似分类；4. 熟练掌握欧氏空间的刻划与相应的变换的刻画；5. 通过对二次型的掌握，了解双线性函数的刻画。

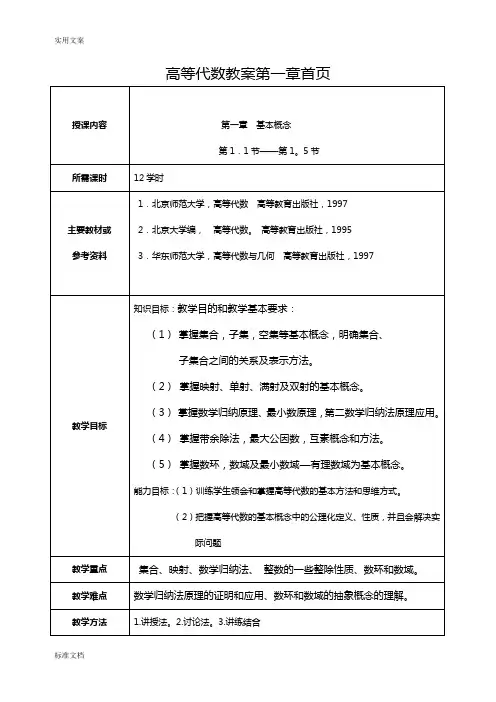
三、各章节授课内容、教学方法第一章：基本概念[教学目的与要求]1.理解集合的概念，了解元素与集合之间的关系、集合与集合之间关系以及几何运算，并掌握相应的算律的证明。

2.了解映射、单射、满射、双射等概念，并会判断其类型。

3.掌握最小数原理和数学归纳法，会用数学归纳法证明相关命题。

4.了解整数整除的一些性质并会用其证明响应的命题。

5.了解数环、数域的概念，会判断数环和数域。

[教学重点与难点] 数学归纳法、判断数环和数域[授课方法] 以课堂讲授为主，课堂讨论、习题课及自学为辅[授课内容]第一节集合第二节映射第三节数学归纳法第四节整数的一些整除性质第五节数环和数域第二章：多项式[教学目的与要求]1. 理解数域F上一元多项式的定义,多项式相乘,次数,一元多项式环等概念。

第2章 高等代数张禾瑞

的最高次项,非负整数n叫做多项式
a0 a1x a2 x 2 an x n an 0 的次数. 记作
0 f x
注：
系数全为零的多项式没有次数,这个多项式叫做 零多项式，记为 0 .
2.1.4 多项式的运算
多项式的加法
给定数环R上两个多项式
f x a0 a1x a2 x 2 an x n gx b0 b1x b2 x 2 bm x m
那么由上面定理的证明得 f xgx 0
推论2 f xgx f xhx, f x 0 gx hx
证 由 f xgx f xhx得 f xgx hx 。但 f x 0
所以由推论1必有 gx hx 0 ,即
gx hx
例 当 a,b, c 是什么数时，多项式
f x ax3 bx 2 c b x3 x 2
f x a0 a1x a2 x 2 an x n , an 0
gx b0 b1x b2 x 2 bm x m , bm 0
且 m n 那么
f x gx a0 b0 a1 b1 x a2 b2 x 2 an bn x n （1）
f xgx a0b0 a0b1 a1b0 x anbm x nm
数为零的项；若是某一个i次项的系数是1 ，那 么这个系数可以省略不写。
2.1.2 相等多项式
定义
若是数环R上两个一元多项式 , f (x) 和g (x)有完全 相同的项,或者只差一些系数为零的项, 那么 f (x) 和 g (x)就说是相等 .
f (x) = g (x)
2.1.3 多项式的次数
an xn叫做多项式 a0 a1 x a2 x 2 an x n an 0
按降幂书写:
f x a0 x n a1 x n1 an1 x an g x b0 x m b1 x m1 bm1 x bm
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（4）掌握坐标的定义、坐标变换公式、线性空间同构的概念。
（5）掌握齐次线性方程组解空间的理论，并能运用这些理论于论证和计算。
能力目标：（1）训练学生能熟练应用基、维数、维数公式理论解决问题。
（2）能应用矩、坐标变换公式、线性空间同构、齐次线性方程组解空间的理论论证和计算。
教学重点
向量空间的定义和性质，子空间的定义及充要条件、线性相关性及其理论、替换定理、基、维数、维数公式及相关的理论，子空间的运算和等价命题、坐标的定义、坐标变换公式、线性空间同构、齐次线性方程组解空间的理论。
（4）掌握矩阵相似于对角阵的条件及特征向量是线性无关的，用其证明问题。
（5）掌握不变子空间的概念和性质。
（6）利用线性变换进行相关论证。
能力目标：（1）会求线性变换在基下的矩阵、矩阵的特征值和特征向量、能应用线性变换与矩阵相似理论论证问题。
（2）会判断一个子空间是否为线性变换的不变子空间。
教学重点
线性映射，线性变换的定义与运算规则；线性变换在基下的矩阵、线性变换与矩阵对应关系。矩阵特征值和特征向量的概念及求法；矩阵相似于对角阵的条件，不变子空间的概念和性质。
（2）掌握多项式的基本理论中的公理化定义、性质，并且能应用这些理论进行推理论证、计算和解决问题。
教学重点
一元多项式的定义和运算、整除性、最大公因式、分解、重因式、
多项多函数、根，复数域、实数域和有理数域上多项式。
教学难点
整除性、最大公因式的存在、重因式、多项多函数、根，复数域、实数域和有理数域上的不可约多项式、算术基本定理。
教学重点
集合、映射、数学归纳法、 整数的一些整除性质、数环和数域。
教学难点
数学归纳法原理的证明和应用、数环和数域的抽象概念的理解。
教学方法
1.讲授法。2.讨论法。3.讲练结合
教学内容及
时间安排
§1 集合 2学时
§2 映射 2学时
§3 数学归纳法 2学时
§4 整数的一些整除性质 2学时
§5 数环和数域 2学时
授课内容
第四章线性方程组
第4．1节——第4。3节
所需课时
12学时
主要教材或
参考资料
1．北京师范大学高等代数高等教育出版社，1997
2．北京大学编高等代数高等教育出版社，1995
3．华东师范大学高等代数与几何高等教育出版社，1997
教学目标
知识目标：教学目的和教学基本要求：
（1）掌握矩阵三种初等变换的意义
（2）掌握n阶行列式的基本理论、性质，并且能应用这些理论进行n阶行列式的计算以及论证问题。
教学重点
n阶行列式的定义和基本性质、行列式的依行依列展开、克拉默定理、
熟练掌握用化上三角形式、依行依列展开法、以及用行列性质、范德蒙
行列式等方法计算行列式，证明行列式的性质及基本理论。
教学难点
子式、余子式、代数余子式及行列式的依行依列展开、克拉默定理应用、
教学方法
1.讲授法。2.讨论法。3.讲练结合
教学内容及
时间安排
§1 一元多项式的定义和运算2学时
§2 多项式的整除性4学时
习题课2学时
§3 多项式的最大公因式2学时
§4 多项式的分解2学时
习题课2学时
§5 重因式2学时
§6 多项多函数，多项式的根2学时
习题课2学时
§7 复数和实数域上多项式2学时
§8 有理数域上多项式4学时
教学难点
线性变换在不同基下的矩阵与矩阵与矩阵的相似。矩阵的特征值和特征向量以及矩阵的相似的关系；矩阵相似于对角阵的条件，不变子空间及空间分解。
能力目标：（1）训练学生能熟练进行矩阵运算，矩阵三种初等变换，求逆矩阵。
（2）能应矩阵三种初等变换，初等矩阵以及矩阵的秩和行列式，矩阵可逆的条件等理论论证问题。
教学重点
矩阵加法，数乘、乘法运算规则，分块运算规则，逆矩阵的定义，可逆的条件及用伴随矩阵及初等变换两种求逆矩阵的方法，初等变换方法求矩阵的秩，能用分块矩阵求某些分块阵的逆矩阵。初等变换与初等矩阵的关系，矩阵秩定义及等价叙述，初等矩阵以及矩阵的秩和行列式
2005年2月28日
高等代数教案第二章首页
授课内容
第二章多项式
第2．1节——第2。8节
所需课时
28学时
主要教材或
参考资料
1．北京师范大学高等代数高等教育出版社，1997
2．北京大学编高等代数高等教育出版社，1995
3．华东师范大学高等代数与几何高等教育出版社，1997
教学目标
知识目标：教学目的和教学基本要求：
（2）掌握逆矩阵的定义，可逆的条件及简单的运算性质。
（3）熟练掌握用伴随矩阵及初等变换两种求逆矩阵的方法，会用初
变换方法求矩阵的秩，能用分块矩阵求某些分块阵的逆矩阵。
（4）了解初等变换与初等矩阵的关系，掌握矩阵秩定义及等价叙述
掌握矩阵等价分解的形式。
（5）能用某些概念和性质进行初等的推理和证明，特别是用等价分解的方法证明某些问题。
习题课 2学时
学习指导
1.复习教材和笔记中本章内容。
2.让学生阅读北京师范大学，高等代数 第一章
3.让学生阅读《高等代数辅助教材》 第一章。
作业及思考题
教材第一章习题：第6页：6、7； 第14页：5、10；第18页：1、4、5；
第29页：2、4、5；第25页：3、5。
教研室审阅意见
同意上述安排。
教研室主任签字：王书琴
教学目标
知识目标：教学目的和教学基本要求：
（1）掌握排列、n阶行列式的定义和基本性质
（2）掌握子式、余子式、代数余子式及行列式的依行依列展开，克拉默定理。
（3）熟练掌握用化上三角形式，依行依列展开法，以及用行列式性质，建立递推公式，克拉默定理等方法计算行列式，证明行列式的性质及基本理论。
能力目标：（1）训练学生领会和把握n阶行列式的定义和基本性质。
1训练学生领会和把握阶行列式的基本理论性质并且能应用这些理论进行阶行列式的定义和基本性质行列式的依行依列展开克拉默定理熟练掌握用化上三角形式依行依列展开法以及用行列性质行列式等方法计算行列式证明行列式的性质及基本理论
高等代数教案第一章首页
授课内容
第一章 基本概念
第1．1节——第1。5节
所需课时
12学时
（1）掌握一元多项式的概念和运算规则，整除互素的概念及简单性质并能进行相关论证。
（2）掌握最大公因式概念和求法，因式分解定理及有关因式的条件，在复数实数范围内进行因式分解的理论结果。
（3）掌握多项式有理根判别，有理不可约多项式的概念，艾森斯坦判别法及应用。
能力目标：（1）训练学生领会和把握多项式的概念和运算规则。
主要教材或
参考资料
1．北京师范大学，高等代数 高等教育出版社，1997
2．北京大学编， 高等代数。 高等教育出版社，1995
3．华东师范大学，高等代数与几何 高等教育出版社，1997
教学目标
知识目标：教学目的和教学基本要求：
（1）掌握集合，子集，空集等基本概念，
学习指导
1.复习教材和笔记中本章内容。
2.让学生阅读北京师范大学，高等代数第二章
3.让学生阅读《高等代数辅助教材》第二章。
作业及思考题
教材第二章复习思考题：第31页：3；第38页：5、6、7；第48页：6、7、9、10、11；第56页：3、5、6；第59页：3、4、5；第65页：4、7、8；第71页：2、3、4、5；第80页：2、3、4。
（2）掌握消去法解线性方程组的方法
掌握矩阵的秩，线性方程组可解的判别法及有解、无解、唯一解的理论和解法。
能力目标：（1）训练学生理解和领会矩阵三种初等变换的意义
（2）能应用消去法解线性方程组、以及能熟练应用矩阵的秩，线性方程组可解的判别法的理论。
教学重点
矩阵三种初等变换、应用消去法解线性方程组、
矩阵的秩，线性方程组可解的判别法及有解、无解、唯一解的理论和解法。
2.让学生阅读北京师范大学，高等代数第四章
3.让学生阅读《高等代数辅助教材》第四章。
作业及思考题
教材第三章复习思考题：
第152页：1、2、3；第159页：1、2、4、5、6；
第168页：1、2、3、5；第180页：1、2、4。
教研室审阅意见
同意上述安排。
教研室主任签字：王书琴
2005年2月28日
高等代数教案第五章首页
n阶行列式计算、证明行列式的性质及基本理论。
教学方法
1.讲授法。2.讨论法。3.讲练结合
教学内容及
时间安排
§1 线性方程组和行列式2学时
§2 排列2学时
§3n阶行列式4学时
习题课2学时
§4 子式和代数余子式，行列式的依行依列展开4学时
§5 克拉默规则2学时
习题课2学时
学习指导
1.复习教材和笔记中本章内容。
教学难点
矩阵运算及运算规则、矩阵可逆条件及求逆矩阵的方法，求矩阵的秩。初等变换与初等矩阵的关系，矩阵乘积的秩和矩阵乘积的行列式。
教学方法
1.讲授法。2.讨论法。3.讲练结合
教学内容及
时间安排
§1 矩阵的运算2学时
习题课2学时
§2 可逆矩阵，矩阵乘积的行列式4学时
§3 矩阵的分块2学时
习题课2学时
学习指导
教学难点
矩阵三种初等变换、矩阵的秩，线性方程组可解的判别法及有解、无解、唯一解的理论。
教学方法
1.讲授法。2.讨论法。3.讲练结合
教学内容及
时间安排
§1 消元法2学时
§2 矩阵的秩线性方程组可解的判别法4学时
习题课2学时
§3 线性方程组的公式解2学时
习题课2学时
学习指导
1.复习教材和笔记中本章内容。