浅谈分形
- 格式:doc
- 大小:40.00 KB
- 文档页数:5

浅谈分形统计吴争程福州大学管理学院统计系(350002)E-mail:wuzhengcheng618@摘 要:如果真实世界不是按标准正态分布的,那我们在正态的假设前提下所做的统计推断就可能出错。
分形描述一种更符合现实的分布,它承认现实是混乱和复杂的。
分形统计与高斯统计的不同在于如何看待不确定性。
分形认为不确定性不等于随机性,混沌系统是在随机的初始条件按照特定规则产生的,是随机性和确定性的结合,是局部随机和全局秩序。
其实高斯统计是分形混沌方法的特例。
认识分形的意义在于排除先验思想的干扰,真正认清要研究的问题和对象。
关键词:分形 混沌 统计1.什么是分形和分形统计分形(Fractal)是关于动力系统或超复杂系统的轨迹在某一空间上的维数不是整数而是分数的一种说法。
分形最早源于几何学概念,可以用来描述大多数自然形状和时间序列。
分形认为事物是不可逆的,有时间方向上的变化;分形对象具有广泛的规模变化范围;分形用分形维来描述对象是如何充满空间的,分形是可以是粗糙的,不连续的,它的维数可以是整数的也可以是分数的,它不像传统的认为物体只有整数维:一维直线、二维平面、三维立体。
分形形状在空间上显示自相似性,分形时间序列在时间上显示自相似性。
简单的说,分形是指一个对象,其部分以某种方式与整体相关,其各个组成部分是自相似的。
一切具有分形性质的形状或序列,其特点在于局部的随机性和整体全局的秩序。
分形认为不确定性不等于随机性,不确定性是以初始条件的敏感性为前提,并由此反映过程的稳定与不稳定性。
分形分布具有如下特征:(1)自相似性:只要特征指数α和偏斜度参数β保持不变,无论规模参数c如何变化均不会改变同一范围内的概率。
序列是无穷可分的,具有自相似的统计结构。
(2)跳跃性(非连续性):分形分布的胖尾是由反馈效应导致的,在时间序列里的反馈效应在过程当中产生了跳跃。
分形过程中的大变化是从少量的大变化产生的,而不是正态分布中所暗示的大量的小变化产生。

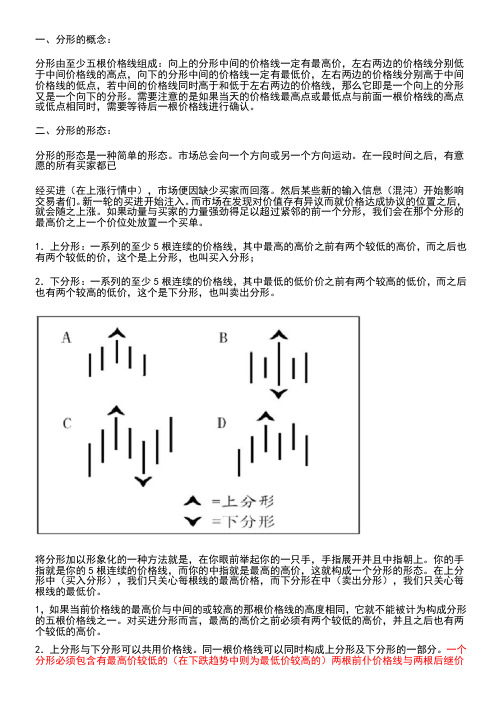
一、分形的概念:分形由至少五根价格线组成:向上的分形中间的价格线一定有最高价,左右两边的价格线分别低于中间价格线的高点,向下的分形中间的价格线一定有最低价,左右两边的价格线分别高于中间价格线的低点,若中间的价格线同时高于和低于左右两边的价格线,那么它即是一个向上的分形又是一个向下的分形。
需要注意的是如果当天的价格线最高点或最低点与前面一根价格线的高点或低点相同时,需要等待后一根价格线进行确认。
二、分形的形态:分形的形态是一种简单的形态。
市场总会向一个方向或另一个方向运动。
在一段时间之后,有意愿的所有买家都已经买进(在上涨行情中),市场便因缺少买家而回落。
然后某些新的输入信息(混沌)开始影响交易者们。
新一轮的买进开始注入。
而市场在发现对价值存有异议而就价格达成协议的位置之后,就会随之上涨。
如果动量与买家的力量强劲得足以超过紧邻的前一个分形,我们会在那个分形的最高价之上一个价位处放置一个买单。
1.上分形:一系列的至少5根连续的价格线,其中最高的高价之前有两个较低的高价,而之后也有两个较低的价,这个是上分形,也叫买入分形;2.下分形:一系列的至少5根连续的价格线,其中最低的低价价之前有两个较高的低价,而之后也有两个较高的低价,这个是下分形,也叫卖出分形。
将分形加以形象化的一种方法就是,在你眼前举起你的一只手,手指展开并且中指朝上。
你的手指就是你的5根连续的价格线,而你的中指就是最高的高价,这就构成一个分形的形态。
在上分形中(买入分形),我们只关心每根线的最高价格,而下分形在中(卖出分形),我们只关心每根线的最低价。
1,如果当前价格线的最高价与中间的或较高的那根价格线的高度相同,它就不能被计为构成分形的五根价格线之一。
对买进分形而言,最高的高价之前必须有两个较低的高价,并且之后也有两个较低的高价。
2.上分形与下分形可以共用价格线。
同一根价格线可以同时构成上分形及下分形的一部分。
一个分形必须包含有最高价较低的(在下跌趋势中则为最低价较高的)两根前仆价格线与两根后继价格线:在买进分形中,我们只关心每根价格线的最高价;在卖出分形中,我们只关心每根价格线的最低价.三、分形的种类:分形买进信号位于上半部分,分形卖出信号位于下半部分。

分形在建筑造型设计中的应用探讨
分形是一种几何形态,具有自相似性的特点,常被用于建筑造型设计中。
它可以将简
单的几何形状无限重复,并生成复杂而美丽的建筑形态。
本文将探讨分形在建筑造型设计
中的应用。
分形可以用于建筑的外观设计。
通过将分形几何形状应用于建筑表面,可以创造出独
特的外观效果。
这种设计可以使建筑在视觉上更加丰富,吸引人们的目光。
将分形形状应
用于建筑外墙的装饰,可以产生出错综复杂的几何图案,给人以立体感和动态感。
分形还可以用于建筑的结构设计。
通过将分形几何形状应用于建筑结构中,可以提供
更好的结构稳定性和抗风性能。
分形结构的特点是具有多层次的组织结构和多尺度的形态,可以将力学负荷分散到各个部分,提高了结构的稳定性。
分形结构还可以减少建筑的材料
使用量,降低施工成本。
分形可以用于建筑的空间布局设计。
通过将分形几何形状应用于建筑内部的空间布局,可以创造出多样化的空间体验。
通过分形形状的重复和变形,可以创造出错落有致的楼梯
空间,使人们在行走的过程中感受到不同的空间层次和节奏感。
分形在建筑造型设计中的应用非常广泛。
它可以用于建筑的外观设计、结构设计、空
间布局设计和环境设计等方面。
分形的特点是可以将简单的几何形状无限重复,并生成复
杂而美丽的建筑形态。
通过应用分形,可以使建筑更加个性化、稳定、美观,并提供丰富
多样的空间体验。
相信随着科学技术的进步,分形在建筑设计中的应用会越来越广泛。

分形理论概述范文
分形(fractal)是一种多尺度的普遍几何结构,可以在物理、化学、生物学等多个学科中发现。
它的定义是“在一定范围内具有相同结构的几
何结构”。
它以极好的逼真度表示自然界的复杂结构,并具有丰富而细腻
的结构。
分形理论是一种解释复杂性和自相似性的抽象理论。
它以上帝视角试
图诠释宇宙的样式和结构,以更深层次的视角来描述自然界的秩序和复杂性,并且可以揭示宇宙的发展规律。
它为解释自然界的许多复杂问题提供
了一个新的途径和方法,从而促进了一系列学科教育、学习、研究和应用
的发展。
分形理论的主要内容主要由三部分组成,分别是:(1)分形几何学,
它探索和研究的是自然界中可以表示为无限复杂结构的几何形状。
(2)分
形演化论,它试图探讨宇宙中各种复杂系统的演化机理。
(3)分形分析理论,它研究多尺度系统的结构,并认为复杂系统在不同尺度上都具有相同
的基本结构。
分形理论的基本概念是复杂性和自相似性,也就是说,复杂的系统在
不同尺度上具有相同的性质。
它采用多尺度的视角来描述宇宙中的系统,
试图把宇宙的复杂性抽象化,以更深层次的视角来描述宇宙的秩序和复杂性。

生物学中的分形及其应用分形是一种自相似的几何形态,其外貌可以在各种尺度下重复出现。
它的概念起源于20世纪60年代,由于它的独特性质和广泛适用性,被广泛应用于自然科学和人文科学领域。
在生物学中,分形被用于研究生物体的结构和生物过程的动态变化。
本文将从不同角度探讨生物学中分形的应用。
一、分形在生物组织的研究中的应用生物组织的形态复杂、层次分明,分形的自相似形态是其最基本特征之一。
通过分析生物组织的形态特征,可以对生物组织的结构和功能进行探究。
目前,分形被广泛应用于生物组织病理学和分子生物学领域。
研究人员通过分析组织切片的图像,对生物组织中不同分支的分形维度变化进行研究,从而揭示生物组织的内在规律。
二、分形在生物图像处理中的应用生物图像处理是分析生物物体结构和功能的重要手段。
以往的图像处理方式多为基于几何模型的算法,缺乏考虑生物物体内在规律的信息。
而分形则通过自相似形态,在光学显微镜和计算机成像技术中实现了深入应用。
分形的优势在于它可以通过统计量描述复杂的分形图像,是一种有效的生物图像分析方法。
在分形应用于生物图像处理中,不仅可以对生物图像的分形特征进行描述,而且还可以发现其生物学意义。
三、分形在生物信号处理中的应用生物信号处理是诊断和治疗领域中的重要分支之一。
分形在生物信号处理中也表现出了其独特优势。
例如,在对脑电信号进行分析时,可以通过分析多种频谱分析手段和分形的方法,获取脑电信号的丰富信息,提高诊断效率。
四、分形在生物进化和系统演化中的应用生物进化和系统演化是生物学的两个核心问题。
分形在生物进化和系统演化中的应用可以揭示生物进化过程中的内在规律,发现物种间的相关性,并通过分析不同生物的分型特征,得出它们在系统演化中的本质联系。
总的来说,分形在生物学中的应用是广泛的。
它的独特性质使得它在探索生命科学的基本问题上具有巨大的潜力。
未来,随着相关技术的不断发展,分形在生物学中的应用还将继续拓展。
浅谈高分子材料学中的分形浅谈高分子材料学中的分形[摘要]分形学目前已涉及诸多科学领域与生活领域,由于具有分形特性的物质可能具有某种特殊性质及功能,从而促使科学工作者们去研究分形的物理、数学及其他方面的机制,探索无序系统内部隐含的某种规律,并用分形维数值将无序系统有序化。
[关键词]分形自相似分维高分子分形理论与耗散结构理论、混沌理论被认为是70年代科学上的三大发现。
1967年曼德布罗特(B.B.Mandelbort)在美国权威的《科学》杂志上发表了题为《英国的海岸线有多长?》的著名论文。
指出海岸线在形貌上是自相似的,也就是局部形态和整体形态的相似。
实际上,具有自相似性的形态广泛存在于自然界及社会生活中,曼德布罗特把这些部分与整体以某种方式相似的形体称为分形(fractal)。
并在此基础上,形成了研究分形性质及其应用的科学,也就是现在的分形理论(fractaltheory),自相似原则和迭代生成原则是分形理论的重要原则。
由于分形理论研究的特殊性,以及他在自然界应用的广泛性,目前分形理论已迅速成为描述、处理自然界和工程中非平衡和非线性作用后的不规则图形的强有力工具。
自分形理论发展以来,国内外对分形理论在各方面的应用进行了大量的理论和实践,材料学中也一样,分型理论目前已渗透到了材料学的各个领域,尤其是高分子材料,下面就分形理论在高分子材料学中的应用做一浅议。
一、分形维数的测定方法根据研究对象的不同,大致可以分为以下五类:改变观测尺度求维数;根据观测度关系求维数;根据相关函数求维数;根据分布函数求维数;根据频谱求维数,分形在材料科学中应用时,一般应用的测定分维方法是:盒维数法、码尺法和小岛法。
二、分形理论在高分子结构中的研究(一)高分子链结构中的分形由于高分子尺寸随链结构象而不断变化,对这类问题的处理属于统计数学中的“无规飞行”。
但若从分形的角度来看,则高分子具有明显的分形特征并可以跟踪监测。
对高分子中普遍存在的自回避行走也是如此,只是表现出不同的分形行为。
浅谈分形曼德布罗(B. B. Mandelbrot)说过:“云不是球形的,山不是锥形的,海岸不是圆形的。
”在自然界中,许多物体的形状和现象是十分复杂的:纵横交错的江河流域,婉转悦耳的古琴音乐中的旋律,蜿蜒盘旋的山岳高峰,星际空间物质的分布,尘粉无规则运动的轨迹,人体复杂的血管分布,如此等等。
像如此不定型的东西,在欧式几何中是无法解释分析的。
因此“分形”应运而生。
说到分形(fractal),先来看看分形的定义。
分形这个词最早是分形的创始人曼德布罗提出来的,他给分形下的定义就是:分形是由一些与其整体以某种方式相似的部分所组成的形体。
很显然,在曼德布罗的分形定义中,含有“不规则”和“支离破碎”的意思。
但是迄今为止,分形还没有非常具体明确的科学定义。
1989年法尔科内提出类似但较为全面的定义:(i)分形集都具有任意小尺度下的比例细节,或者说它具有精细的结构。
(ii)分形集不能用传统的几何语言来描述,它既不是满足某些条件的点的轨迹,也不是某些简单方程的解集。
(iii)分形集具有某种自相似形式,可能是近似的自相似或者统计的自相似。
(iv)一般,分形集的“分形维数”,严格大于它相应的拓扑维数。
(v)在大多数令人感兴趣的情形下,分形集由非常简单的方法定义,可能以变换的迭代产生。
定义总是抽象的,下面先介绍几种理想的或典型的分形结构,以便对定义中的分形集,自相似性,分形维数,拓扑维数,迭代等有所了解,从而对分形有具体而形象的认识。
(1)康托尔集(Cantor set)。
假设一条为单位长度的线段,将其设为基本区间[0,1],把它三等分,分点分别为1/3,2/3,去掉该线段中间的三分之一,这样留下的部分将是两段长度分别为三分之一的线段,总长度为2/3,用集合表示为[0,1/3] ∪[2/3,1]。
接下去我们再把这两条线段分别去掉中间的三分之一,这时留下的部分将是四条长度各为九分之一的线段,总长度为4/9,用集合表示为[0,1/9] ∪[2/9,1/3] ∪[2/3,7/9]∪[8/9,1]。
如此不断地循环操作,最终得到的点的集合就是康托尔三分集。
这就是一个分形图案。
(如图)由图,显而易见,当线段分到一定程度时,每一个线段的长度将无限接近于0, 但是在原线段的分点1/3,2/3,1/9,2/9,7/9,8/9……处的点又属于这个点集,因而康托尔三分集不是一个空集。
(2)Koch(柯克)曲线。
从平面上一条单位长的直线段开始,在它的1/3和2/3处撑起一个边长为1/3的等边三角形,并去掉这个底边。
在这个变换中,得到一条折线,线段的总长度将增加三分之一,成为4/3。
不断重复这个变换,即对上一步所得图案中的每一条线段进行同样的处理,这时,曲线的总长度将按4/3的n次方递增而趋于无穷大,随着n的不断增大,折线的总长度也在不断加大,然而很显然,它并不会铺满整个平面。
这就是柯克曲线。
康托尔点集柯克曲线由以上的理想的分形几何图形,我们会发现它们都是一种很玄妙的图形。
从分形(fractal)的词义简单理解,分形具有破碎的和不规则的含义,在任意小的尺度上都有着精细的结构,如果将其分为不同的部分,不论大小,每一部分的形状都和整体一样。
从理论上说,分形可以定义为“非整数维数的点集”。
集合是分形理论中的一个基本数学概念.一个分形集实际上就是某些特殊的点所组成的集合。
就如康托尔三分集所展现的,这个分形就是由经过特别方式而选取出来的无数点所构成的点集。
从分形图案的特点去理解它。
分形图案有一系列有趣的特点,它们都具有可分和相似性或自仿射性,对某些变换的不变性、内部结构的无限性等。
我认为分形的自相似性是指把小区域的分布放大后便得到了大区域的分布,也就是不论采取怎样大小的表达对它进行测量时,分形图形都不变。
自仿射性是指:把考察的对象的一部分沿各个方向以不同比例放大后,其形态与整体相同或相似。
如(柯克)曲线,这种自相似可以完全规则的自相似,也可以是无规则的自相似。
分形图案往往和它自身的一部分相似,换句话说,把它的一部分按一定的尺度放大,就又会得到它自身(可能是确切地,也可能是近似地)。
我们还会发现分形图案内部结构复杂精细。
总之这种自相似性所产生的明显后果就是在不同程度的放大后,图形的样子看起来基本相同或相似的。
而具有自相似性或自仿射性结构的体系就是分形体。
从维数方面看,我们会发现分形的另一个特征就是维数不必为整数。
分形维数是用来描述分形结构疏密分布的一个特征量。
分形维数分为拓扑维数、豪斯多夫维数、容量维数和相似维数。
下面就康托尔三分集和Koch(柯克)曲线的容量维进行介绍。
容量维数是从被测几何体容量大小进行分析计算的。
由上面的康托尔三分集,我们知道,随着不断的三等分再去掉中间的三分之一,康托尔集最后是由无数个处处稀疏的点组成的,它不是一个空集,因此它的容量维数必定大于0,同时又因为这些点是稀落的,并不能填满整条线段,因此它的维数又小于1,所以康托尔三分集是一个维数在0和1之间的分形图案,它的维数并不是整数。
同理,可以发现Koch(柯克)曲线是在不断地三等分和加边,最终得到一条长度不断增大的折线,显然Koch(柯克)曲线这个分形结构的容量维不会比1小,但是尽管它的长度不断扩大,边不断增多,最终它并不会铺满整个平面,所以它的容量维数不会大于2。
综上柯克曲线是一种维数大于1而小于2的分形图案。
在欧式几何中,所研究的形状的维数都是整数,分数维是不存在的,但是分形就具有这种怪异的性质,而且在大自然、社会生活中普遍存在。
理想的分形结构还有席尔宾斯基垫片(S I e r p I n s k i gasket),席尔宾斯基地毯(Sierpinski carpet),门杰海绵(M e n g e r sponge)等,但是这些都是理想的人为的规则自相似结构,在真实的客观世界中,物体总要受到外界环境或自身固有的各种随机性作用,这使得在现实生活中的分形结构不可能是严格的规则自相似,而只能是大体上或者大部分的自相似,也就是无规分形。
如在显微镜下观察落入溶液中的一粒花粉,会看见它不间断地做无规则运动,也就是物理中的布朗运动,这是花粉在大量液体分子的无规则碰撞下表现的平均行为。
布朗粒子的轨迹,由各种尺寸的折线连成。
但是这些折线并不代表花粉实际运动中的轨迹,只要有足够的分辨率,或者将记录的时间缩短,就可以发现原以为是直线段的部分,其实由大量更小尺度的折线连成。
又如在某些电化学反应中,电极附近沉积的固态物质,以不规则的树枝形状向外增长。
受到污染的一些流水中,粘在藻类植物上的颗粒和胶状物,不断因新的沉积而生长,成为带有许多须须毛毛的枝条状。
还有微观世界中晶体的生长;宏观世界中太阳黑子的活动,奇形怪状的星云分布,等等;曲折绵延的海岸线,河流的走向,树枝的分叉以及地震震级的分布等;就连我们人体血液循环系统中血管的分支和脑电波分布都是分形的。
下面具体介绍几种自然或生活常见的分形现象。
(1)电击穿。
电击穿的种类很多,最常见的就是大气中的闪电。
众所周知闪电是云层间的正电荷和负电荷的电势差超过一定的限度时发生的自然现象。
也就是说云层间的气体受到巨大电流的冲击后被电离了,瞬间变为导体,使得闪电的形状是枝状。
电击穿也可以发生在其他的绝缘体中,但发生电击穿时,所形成的图案却很相似。
电击穿是一种无规则的生长过程,近年来才认识到电击穿所产生的形状是分形,它的分形维约是1.7 。
(2)地震。
地震是地球内部的岩石突然断裂而引起的地球表面的动荡。
地震具有多种分形性质,其中地震的次数在时间上的分布就是一种。
地震研究者采取了分形几何的方法来研究地震在时间上的分布。
其中就运用到了康托尔三分集。
在用于地震时,研究者对康托尔三分集进行了改造,仍是把一条单位长度的直线段进行三等分,但去掉的不是中间的三分之一,而是随机地任意去掉三个线段中的一个。
这样产生了无规则的康托尔三分集。
利用康托尔集是为了说明地震的群集现象,并且分割不是无限次进行下去的,因为在有限的时间间隔内,地震并不是无限次的。
由此计算出的分形维数可以用来描述群集的程度:群集的程度越高,分形维的值就越大(3)雪花。
在显微镜下,无论是1毫米、1/10毫米还是1/1000毫米的尺度,雪花边缘上的图案和形状几乎是相同的。
分形在生活中的应用十分普遍。
分形理论的根本出发点是局部与整体的相似性。
应用于预测时,往往是由局部推及整体,探索事物的发展规律。
因而分形理论在滑坡预测预报中有着重要的应用。
同时,分形理论还应用于医学。
美国克拉克森大学的研究人员发现,与健康细胞相比,癌细胞在外观上具有更为显著的分形特征。
以此为依据,他使用新的图像检测方法,对来自12位患者的300个细胞样本进行检查的结果表明,其准确度接近100%。
据此他断言,基于物理的方法,将达到甚至超过传统生化检测方法在单细胞水平上的检测能力。
在服饰艺术,绘画作品,动漫设计等方面,分形几何也得到了广泛的应用。
传统的图案设计受到人脑想象力的限制,而且后续的修改过程也比较烦琐,而利用分形的自相似性,再结合计算机,可以在短时间内构造出千变万化而又具有任意高分辨率结构的分形图案。
不止这样,分形还可以用来描述许多其他领域的事物,如股票市场的价位变化、湍流的波动起伏、地质活动、行星轨道、动物群体行为、社会经济学模式,甚至音乐也可以通过图形来表达。
在当今的社会中,分形已经得到了广泛的应用,分形理论应用的研究前景是不容小视的,它具有强大的潜力,在不久的将来必定会开阔更广大的天空!。