线性代数-向量及其线性运算
- 格式:ppt
- 大小:2.56 MB
- 文档页数:54



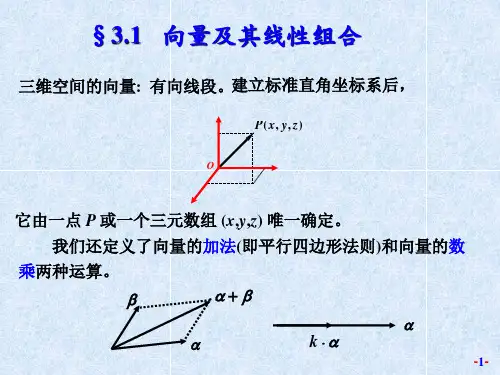

向量的线性运算向量的加法和数乘向量的线性运算:向量的加法和数乘向量是数学中一个重要的概念,它在许多领域中都有广泛的应用。
在线性代数中,向量的线性运算是一项基础且重要的内容。
本文将重点介绍向量的加法和数乘两种线性运算,以及它们的性质和应用。
一、向量的加法向量的加法是指将两个向量相应位置上的元素进行相加得到一个新的向量。
设有两个向量:向量A = (a₁, a₂, ..., aₙ)和向量B = (b₁,b₂, ..., bₙ),则它们的加法可表示为:A +B = (a₁ + b₁, a₂ + b₂, ..., aₙ + bₙ)其中,a₁ + b₁表示A和B的第一个元素相加,a₂ + b₂表示A和B的第二个元素相加,以此类推。
需要注意的是,参与加法运算的两个向量必须有相同的维度,即拥有相同数量的元素。
向量的加法具有以下性质:1. 交换律:对于任意两个向量A和B,有A + B = B + A。
即向量的加法满足交换律,顺序可以交换而不影响结果。
2. 结合律:对于任意三个向量A、B和C,有(A + B) + C = A + (B +C)。
即向量的加法满足结合律,可以按照任意顺序进行多次加法运算。
3. 零向量:对于任意向量A,存在一个全零向量0,使得A + 0 = A。
即任何向量与零向量进行加法运算,结果仍为原向量本身。
向量的加法有着广泛的应用,例如在力学中,将多个力的作用效果用向量的加法表示;在几何学中,将多个向量的位移用向量的加法表示等等。
二、向量的数乘向量的数乘是指将一个实数乘以一个向量的每个元素得到一个新的向量。
设有一个向量A = (a₁, a₂, ..., aₙ),实数k,则它们的数乘可表示为:kA = (ka₁, ka₂, ..., kaₙ)即向量A的每个元素都乘以k得到新的元素。
这里的实数k称为标量,而向量A称为向量kA的标量倍。
需要注意的是,标量与向量进行数乘时,不改变向量的维度。
向量的数乘具有以下性质:1. 结合律:对于任意实数k₁和k₂以及向量A,有(k₁k₂)A =k₁(k₂A)。

向量的线性运算向量是线性代数中的重要概念,线性运算是对向量进行数学操作的方法。
本文将介绍向量的线性运算包括加法、减法、数乘,以及向量的线性组合。
一、向量的加法向量的加法是指将两个向量相加得到一个新的向量,符号为“+”。
设有向量A和向量B,记作A+B=C,其中C是向量A和向量B的和向量。
向量的加法满足以下几个性质:1. 交换律:A+B=B+A2. 结合律:(A+B)+C=A+(B+C)3. 零向量:对于任意向量A,有A+0=A,其中0是零向量,即所有分量都为0的向量。
二、向量的减法向量的减法是指将一个向量减去另一个向量得到一个新的向量,符号为“-”。
设有向量A和向量B,记作A-B=C,其中C是向量A和向量B的差向量。
向量的减法可以转化为向量的加法,即A-B=A+(-B),其中-表示取反操作。
三、向量的数乘向量的数乘是指将一个向量乘以一个实数得到一个新的向量。
设有向量A和实数k,记作kA=B,其中B是向量A的数乘结果。
向量的数乘满足以下性质:1. 分配律:k(A+B)=kA+kB2. 结合律:(kl)A=k(lA),其中k和l为实数四、向量的线性组合向量的线性组合是指将若干个向量按照一定的权重进行相加得到一个新的向量。
设有向量A1、A2、...、An和实数k1、k2、...、kn,向量的线性组合记作k1A1+k2A2+...+knAn。
向量的线性组合可以看作是向量的加法和数乘运算的组合。
向量的线性运算在向量空间中有着重要的应用。
通过向量的线性组合,我们可以表示出向量空间中的各种线性关系,诸如线性相关性、线性无关性、生成子空间等概念。
在实际问题中,向量的线性运算也有广泛的应用。
例如,物理学中常用向量的线性组合来表示力、速度、加速度等物理量;经济学中则常用向量的线性组合来表示商品的组合、市场的供求关系等。
综上所述,向量的线性运算包括加法、减法、数乘和线性组合。
通过这些运算,我们可以对向量进行各种数学操作,方便地进行向量的运算和分析,也为解决实际问题提供了有力的工具。

向量的线性运算线性运算是数学中的一个重要概念,它在许多不同领域中都有广泛的应用。
在线性代数中,线性运算指的是对向量进行加法、标量乘法和一些其他操作的过程。
这些操作可以用于解决很多实际问题,在计算机科学、物理学、工程学以及经济学等领域都有重要应用。
在线性代数中,一个向量通常可以表示为一个由多个数值组成的有序集合。
例如,一个二维向量可以表示为(x, y),其中x和y分别表示向量在x和y轴上的分量。
对于一个n维向量,可以用类似的方式表示为(x1, x2, ..., xn)。
首先,让我们来看一下向量的加法。
向量的加法是指两个向量按照对应分量相加的操作。
例如,对于向量a=(2, 3)和向量b=(1, -1),它们的和a+b=(2+1, 3+(-1))=(3, 2)。
向量的加法可以用于解决很多实际问题,如计算机图形学中的坐标变换、力学中的力合成等。
其次,我们来介绍一下向量的标量乘法。
向量的标量乘法是指一个向量与一个实数相乘的操作。
例如,对于向量a=(2, 3)和标量c=2,它们的标量乘积c*a=(2*2, 3*2)=(4, 6)。
向量的标量乘法可以用于调节向量大小、计算向量的线性组合等。
除了加法和标量乘法之外,还有一些其他的向量运算。
例如,向量的点积和向量的叉积是两个非常重要的运算。
向量的点积是指两个向量按照对应分量相乘再相加的操作。
例如,对于向量a=(2, 3)和向量b=(1, -1),它们的点积a·b=2*1+3*(-1)=2-3=-1。
向量的点积可以用于计算向量的长度、计算向量之间的夹角等。
向量的叉积是指两个三维向量按照一定规则进行运算得到的新向量。
向量的叉积在物理学中常用于计算力学中的力矩、电磁学中的磁场等。
线性运算在许多实际问题中都有广泛的应用。
在计算机科学中,线性运算被广泛应用于计算机图形学中的坐标变换、计算机视觉中的特征提取等。
在物理学中,线性运算被广泛应用于力学中的力合成、电磁学中的电磁场计算等。

向量的线性运算及其性质向量是线性代数中的重要概念,是指由一组数按照一定规律排列而成的有序数列。
向量的线性运算是指在向量空间中,对两个或多个向量进行数学运算的过程,其中包括向量加法和数量乘法等两种基本运算。
一、向量加法向量加法是向量运算中最基本的一种运算方式。
在向量空间中,向量加法的定义是两个向量相同位置上的数值相加。
例如,对于向量a=(a1,a2,a3)和b=(b1,b2,b3),它们的加法定义为:a+b=(a1+b1,a2+b2,a3+b3)在向量加法中,满足加法交换律和结合律。
即对于任意向量a,b,c,有:a+b=b+a(a+b)+c=a+(b+c)此外,零向量也是一个特殊的向量,它的各个分量都为0,记为0。
对于任意向量a,都有:a+0=a二、数量乘法数量乘法是指一个向量乘以一个常数。
常数也称为标量,表示为k。
例如,对于向量a=(a1,a2,a3),其数量乘法定义为:ka=(ka1,ka2,ka3)在数量乘法中,也满足交换律和结合律。
即对于任意向量a,b 和任意实数k,有:k(a+b)=ka+kb(k1k2)a=k1(k2a)此外,特别地,当k=0时,有:0a=0这个公式表示了任何向量与零向量相乘结果都是零向量。
三、线性组合如果给定一个向量集合,可以通过线性组合的方式来构造出一个新的向量。
线性组合的形式是将每个向量分别与对应的系数相乘后相加,例如:k1a1+k2a2+k3a3其中k1,k2,k3为实数,a1,a2,a3为向量。
线性组合可以看作是向量加法和数量乘法的叠加,它有着很多重要的性质。
线性组合是向量空间中的重要概念,它可以用于描述向量之间的关系。
四、向量空间向量空间是指一组向量所组成的空间,其中的向量可以进行向量加法和数量乘法等线性运算。
向量空间必须满足以下条件:1. 零向量存在并唯一。
2. 加法和数量乘法满足交换律、结合律和分配律。
3. 对于任意向量a,都有它的相反向量-b,使得a+b=0。

第1讲 向量代数—向量及其线性运算主要内容1 向量的概念2 向量的线性运算3空间直角坐标系4利用坐标进行线形运算5向量的模、方向角、投影讲解提纲:第七章 空间解析几何与向量代数在平面解析中. 通过坐标法把平面上的点与一对有次序地数对应起来,就可以把平面上的图形和方程对应起来、统一起来,使得人们既可以用代数方法研究解决几何问题(这是解析几何的基本内容),也可以用几何方法解决代数问题.本章中我们先介绍向量的概念及向量的某些运算,然后再介绍空间解析几何,其主要内容包括平面和直线方程、一些常用的空间曲线和曲面的方程以及关于它们的某些基本问题.这些方程的建立和问题的解决是以向量作为工具的. 正像平面解析几何的知识对学习一元函数微积分是不可缺少的一样,本章的内容对以后学习多元函数的微分学和积分学将起到重要的作用.第一节 向量及其线性运算一、向量的概念.既有大小,又有方向。
例如位移、速度、加速度等等。
二、向量的线性运算:向量的加减法, 向量与数的乘法定理1 设向量0≠a , 那末向量b 平行于a 的充分必要条件是: 存在唯一的实数λ, 使a b λ=.定理1是建立数轴的理论依据. 我们知道,确定一条数轴, 需要给定一个点、一个方向及单位长度. 由于一个单位向量既确定了方向, 又确定了单位长度, 因此, 只需给定一个点及一个单位向量就确定了一条数轴.三、空间直角坐标系特钲四、利用坐标进行线形运算(=+b ak b a j b a i b a z z y y x x )()()+++++(=-b ak b a j b a i b a z z y y x x )()()-+-+- (=aλk a j a i a z y x )()()λλλ++五、向量的模、方向角、投影性质1 ϕcos ||Pr a a j u = (ϕ为向量a与u 轴的夹角);性质2 b j a j b a j u u uPr Pr )(Pr +=+;性质3 a j a j u uPr )(Pr λλ= (λ为实数).例题选讲:1.向量的线性运算例1 化简 13325.25b a a b b ⎛⎫--+-+ ⎪⎝⎭例2 在平行四边形ABCD 中, 设,,AB a AD b == 试用a和b 表示向量,,MA MB MC 和MD, 这里M 是平行四边形对角线的交点.解:由对角线互相平分,所以()2,a b A C A M +==即()2,a b MA -+=于是1()2MA a b =-+,111(),(),()222MC a b MD b a MB a b =+=-=-例3 在x 轴上取定一点O 作为坐标原点. 设A , B 是x 轴上坐标依次为21,x x的两个点, i是与x 轴同方向的单位向量, 证明 21().AB x x i =-2.空间两点间的距离例4 已知点)10,3,4(),4,1,2(B A ,写出以线段AB 为直径的球面方程。


线性代数的基本概念与运算线性代数是数学中的一个重要分支,研究向量空间及其上的线性变换。
它在许多领域中都有广泛的应用,如物理学、计算机科学、经济学等。
本文将介绍线性代数的基本概念与运算,包括向量、矩阵、线性变换等内容。
一、向量的基本概念与运算向量是线性代数中的基本概念之一。
它可以用有序的数对或数列表示,常用箭头表示。
向量有大小和方向两个特征,可以进行加法和数乘运算。
向量的加法是指将两个向量的对应分量相加,数乘是指将一个向量的每个分量乘以一个数。
向量的加法和数乘运算满足一些基本性质,如交换律、结合律和分配律。
这些性质使得向量的运算更加方便和灵活。
通过向量的运算,我们可以描述和计算许多实际问题,如力的合成、位移的计算等。
二、矩阵的基本概念与运算矩阵是线性代数中另一个重要的概念。
它是一个按照长方阵列排列的数表,由行和列组成。
矩阵可以表示向量、线性方程组和线性变换等。
矩阵的运算包括加法、数乘和乘法。
矩阵的加法是指将两个矩阵的对应元素相加,数乘是指将一个矩阵的每个元素乘以一个数,矩阵的乘法是指按照一定规则将两个矩阵相乘。
矩阵的乘法是线性代数中的核心运算之一。
它不仅可以用来解决线性方程组,还可以用来描述线性变换。
矩阵的乘法满足结合律,但不满足交换律。
这一点与普通的数乘运算不同,需要注意。
三、线性变换的基本概念与运算线性变换是线性代数中的重要概念之一,它是指一个向量空间到另一个向量空间的映射,保持向量加法和数乘运算。
线性变换可以用矩阵表示,通过矩阵乘法来描述其作用。
线性变换有许多重要的性质,如保持向量加法和数乘运算、保持零向量、保持线性组合等。
这些性质使得线性变换在实际问题中有广泛的应用,如图像处理、信号处理等。
线性变换的逆变换和复合变换也是线性代数中的重要概念。
逆变换是指将一个向量空间映射回原来的向量空间,复合变换是指将一个线性变换和另一个线性变换相结合。
总结:线性代数是数学中的一个重要分支,研究向量空间及其上的线性变换。