转子找静平衡教学资料
- 格式:doc
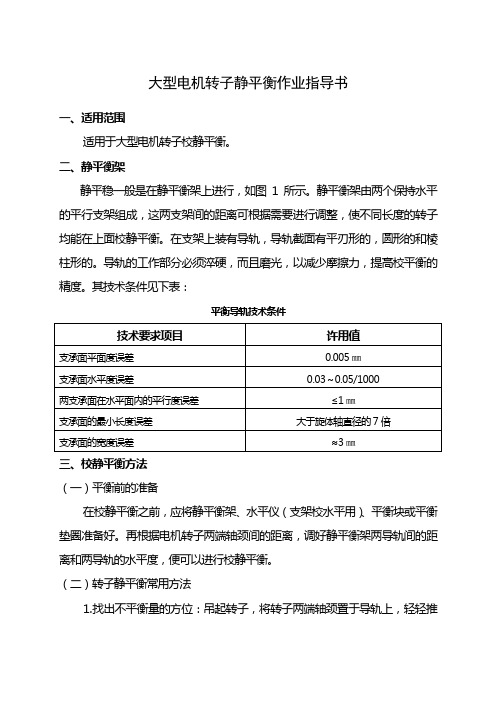
- 大小:278.00 KB
- 文档页数:11

转子静平衡转动机械在运行中有一项重要的技术指标就是振动。
振动要求越小越好。
转动机械振动原因很多,其中以转子质量不平衡而引起的振动最常见。
高速运行的转子即使存在数值很小的质量偏心,也会产生较大的不平衡离心力,这个振动通过支承部件以振动的形式表现出来。
转机长时间的超常振动会导致机组金属材料的疲劳而损坏,转子上的紧固件发生松动,间隙小的动静部件因振动会造成相互摩擦,产生热变形,甚至引起轴弯曲。
现在技术还不可能转动机械的振动,因此规定出振动的允许范围,并以此来衡量运行状态的优劣。
一、 转子分类及刚性转子不平衡现象转子可分为刚性转子与挠性转子两类。
刚性转子是指转子在不平衡力的作用下,转子轴线不发生挠曲变形;挠性转子是指转子在不平衡力的作用下,转子轴线发生挠曲变形。
由于绝对刚性转子的不存在,习惯上把转子在不平衡力的作用下,转子轴线没有显著变形,即挠曲造成的附加不平衡可以忽略不计的转子都作为刚性转子对待。
在转子找平衡工作中,若把转子设定为刚体,则可使转子复杂的埠平衡状态简化为一般的力系平衡关系,从而大大简化找平衡的方法。
假设某转子由两段组成,如图所示。
刚性转子因质量埠平衡产生的埠平衡现象由以下三种类型:(1)两段的重心1G 、2G 处于转子的同一侧,且在同一轴向截面内,如图所示。
静止时转子重心G 受地心引力的作用,转子不能在某一位置保持稳定,这种情况称为静不平衡。
(2)两段的重心1G 、2G 处在同一轴向截面内转子的两侧,如图所示。
若r G r G 21=,则转子处于静平衡状态。
但转动时,其离心力形成一个力偶,转子产生振动,这种情况称为动不平衡。
(3)两段的重心1G 、2G 不在同一轴向截面内,如图所示,这种情况既存在静不平衡,又存在动不平衡,称此情况为混合不平衡。
前两种类型纯属特例,实际上转子的不平衡现象都是以混合不平衡的状态出现的。
二、转子混合不平衡的力系平衡关系假定平面Ⅰ和平面Ⅱ为转子两段加平衡重量的轮盘(为了作图清晰,将轮盘画成矩形),如图所示。

转子(水泵叶轮)的静平衡和动平衡转子(水泵叶轮)的静平衡和动平衡作业指导书 1)静平衡在转子一个校正面上进行校正平衡,校正后的剩余不平衡量,以保证转子在静态时是在许用不平衡量的规定范围内,为静平衡又称单面平衡。
2)动平衡在转子两个校正面上同时进行校正平衡,校正后的剩余不平衡量,以保证转子在动态时是在许用不平衡量的规定范围内,为动平衡又称双面平衡。
2、转子平衡的选择与确定如何选择转子的平衡方式,是一个关键问题。
其选择有这样一个原则:只要满足于转子平衡后用途需要的前提下,能做静平衡的,则不要做动平衡,能做动平衡的,则不要做静动平衡。
原因很简单,静平衡要比动平衡容易做,动平衡要比静动平衡容易做,省功、省力、省费用。
那么如何进行转子平衡型式的确定呢,需要从以下几个因素和依据来确定:1)转子的几何形状、结构尺寸,特别是转子的直径D与转子的两校正面间的距离尺寸b之比值,以及转子的支撑间距等。
2)转子的工作转速。
3)有关转子平衡技术要求的技术标准,如GB3215、API610第八版、GB9239和ISO1940等。
3、转子做静平衡的条件在GB9239-88平衡标准中,对刚性转子做静平衡的条件定义为:"如果盘状转子的支撑间距足够大并且旋转时盘状部位的轴向跳动很小,从而可忽略偶不平衡(动平衡),这时可用一个校正面校正不平衡即单面(静)平衡,对具体转子必须验证这些条件是否满足。
在对大量的某种类型的转子在一个平面上平衡后,就可求得最大的剩余偶不平衡量,并除以支撑距离。
如果在最不利的情况下这个值不大于许用剩余不平衡量的一半,则采用单面(静)平衡就足够了?quot;从这个定义中不难看出转子只做单面(静)平衡的条件主要有三个方面:一个是转子几何形状为盘状;一个是转子在平衡机上做平衡时的支撑间距要大;再一个是转子旋转时其校正面的端面跳动要很小。
对以上三个条件作如下说明: 1)何谓盘状转子主要用转子的直径D与转子的两校正面间的距离尺寸b之比值来确定。


转子找静平衡和转子找动平衡细节2016-08-22郭晓东11、找静平衡的准备工作:(1)准备发一般常用的工具、量具、平衡铁块和仪表;(2)检查现场有无震动和风力的二扰;(3)检查平衡台是否符合质量要求;(4)检查轴的表面粗糙度和轴的弯曲度,椭圆、锥度。
2、静平衡台的种类及要求:(1)轨道平衡台①棱形轨和表面应保持光滑洁静。
②两轨的距离在不防碍叶轮转动情况下,尽量缩小些;两轨道不平行度不超过0.5mm/m,轨道倾斜度不超过0.6mm/m。
③平衡轴要有足够的刚度而不发生变形。
平衡轴的两端轴颈尺寸误差不超过±0.01mm;椭圆度不超过0.02mm,锥度不超过0.02mm;最在弯曲度不超过0.01mm。
④平衡台应稳定固牢靠,当转子在轨道上滚动数次后,其倾斜度和平行度均不发生变化。
(2)双轮转动平衡台:①轮盘应用45—#50钢制作或进行热处理以提高表面硬度。
②轮盘内的轴承应装配紧密且转动灵活。
③轮盘加工表面粗糙为内处圆不同心度不大于0.02mm。
④平衡轴应有足够的刚度来承受叶轮的重垂力面不发生变形,最大弯曲度不超过0.10mm/m;两端轴径误差不超过0.02mm,锥度不超过0.02mm。
⑤轮盘与轴径沿轴向表面应严密接触,不许有缝隙。
⑥轴的水平偏差不超过0.06mm/m。
(3)轴承平衡台:①其轴承应选用磨擦系数小的向心滚珠轴承,配合要紧密且转动灵活。
②轴安装水平度不超过0.06mm/m。
③轴承支架牢固,并有防尘设施。
④平衡轴的要求与前两种平衡台的要求一样。
⑤轴承注入少量的润滑油。
(4)在原设备上找静平衡①应清洗轴承并加入少量稀油润滑。
②拆开对轮连接销钉与电机解列。
③关闭进、出口挡板,必要时应进一步采取减少抽风措施,使叶轮能够自然停下后方能进行静平衡工作。
④盘车应灵活,不许有磨擦,碰撞现象。
2、找平衡的方法:(1)消除显著不平衡:将转子放在平衡台上,给转子一外力使其转动,待转子自由停止后,在其正上方做一记号,连续反复转数次,如果做记号的点仍停止在上方,此点即为轻点,即可在此处试加重量。

转子找静平衡1.找静平衡前,应按叶轮孔径选择一根专用静平衡假轴;2.清理导轨平衡架;3.找正导轨平衡架纵、横向水平;4.找显著静平衡:4.1. 将转子放在平衡架上,轴与轨道垂直,转子在平衡架轨道上往复滚动数次,转子在滚动时,不平衡重量所在位置自然是垂直向下的,作好记号,如果转子停止的位置始终不变,也就是转子垂直向下这一半径位置几次试验都一样,它就是转子偏重的一侧,可以在转子上作出记号;4.2. 在偏重的对侧(即停止时正好轴上方的半径上)试加重块,重块可以用橡皮泥、油灰,也可用橡皮泥、油灰加螺母,试加重块的重量根据反复试验确定,试加重块加上之后,会使转子转到任何位置都能停住;4.3. 称出试加重块重量,此重量为显著不平衡重量;4.4. 去不平衡重量,如是水泵叶轮,应在较重一侧减重量,可用铣床进行铣削,铣削的深度不要超过叶轮盖板厚度的1/3,铣削时可以从试加重块中心向二侧铣削,根据重块重量、铣刀直径、铣削深度、叶轮材质比重计算出弧长,划线进行铣削;4.5. 如果铣削位置与测量的加重块位置不相同,可进行如下换算;P1 =P×(r/r1)式中:P1—铣削重量r 1—铣削处的半径P —测量时加重块的重量r —测量时加重块的直径4.6. 检验除去不平衡重量后的叶轮,重新作静平衡。
如仍有不平衡重量,重复步骤4.1.~4.4.经平衡后,静平衡允许偏差数值近似为叶轮外径值乘以0.025克/毫米。
5.找剩余静不平衡:5.1. 在叶轮上画一配重圆,在这个圆周上减少或增加重块应是比较方便的;5.2. 将配重圆的圆周分八等分,按顺序在等分点上标上编号1、2、3、……8;5.3. 先使1点和轴心共处于一条水平线上,并在1点试加配重,逐渐增加,直到转子失去平衡,并在导轨上开始滚动为止。
并把使转子开始失去平衡的重量记录下来。
其它各点都照样作一遍;5.4. 把八个点所加重量的记录,用坐标的形势表示出来,如图所示:5.5. 从曲线上找出最大配重W最大和最小配重W最小,从而计算出转子剩余静不平衡重量W余:W余=1/2(W最大- W最小)g5.6. 从曲线上找出配重圆上最大配重点的位置(它不一定是八等分点当中的一个点),就在这个位置上加平衡重量W余(或在叶轮对称处去除平衡重量W余),消除剩余静不平衡。
2010年盐城建筑二模参考答案二、判断题:21、A 22、B 23、B 24、B 2 5、A 26、A 27、B 28、B三、填空题:29、2 30、四31、-200MPa 32、11.67KN 53.34KN.m33、0 34、bh3/3 35、0 P 36、7~10mm 37、宽相等 38、棱线交点投影;棱线的积聚投影 39、左 40、主次关系41. 1/200 42. 二平一侧43. 承压完整井44. 结构自防水45、10d最大弯矩46.递减47. 500mm48. 200mm 4 9. 标准值50. 6—12mm51. 可靠性52. 纵向受拉钢筋截面重心受压区边缘53. 0.5%--1.6%四、简答题:54、①清理板面浮渣杂物②浇水湿润,刷1:1素水泥浆,或设隔离层,随铺砼③设分格缝,水泥初凝后取出分格条④施工环境温度5--35oC,养护时间不少于14d55、①已浇砼抗压强度达到1.2②清理砼表面浆膜和松石,并冲洗干净,不得积水③铺一层水泥浆或与砼成分相同的水泥砂浆④分层浇筑和捣实56、①选择和易性好的砂浆,确保砂浆饱满和提高粘结强度②采用“三一”砌筑法③严禁用干砖砌筑57、正截面破坏斜截面破坏纵筋锚固破坏支座处的局部挤压破坏五、计算题:58、RA=15KN RB =15KN59、P=42.39KN60、σmax拉=36.2MPa σmax压=48.3 MPa61、略62、略63、解:(1)验算配箍率ρsv =sb nA sv 1×100%=2001503.502⨯⨯×100%=0.335%>ρsv,min (4分)配箍率满足要求。
(1分)(2)求斜截面承载力 V u =0.7f t bh 0+1.25fyvSA svh 0 (2分) =0.7×1.27×200×460+1.25×300×1503.502⨯×460 =197.5×103N=197.5kN (2分) (3) 复核梁的截面尺寸h W =h 0=h -a s =500-40=460mm (2分)h w /b =460/200=2.3<4.0 (2分)0.25×1.0×9.6×200×460=220.8×103N=220.8kN>V (2分) 截面满足要求。
转子的动平衡和静平衡1、定义1)静平衡在转子一个校正面上进行校正平衡,校正后的剩余不平衡量,以保证转子在静态时是在许用不平衡量的规定范围内,为静平衡又称单面平衡。
2)动平衡在转子两个校正面上同时进行校正平衡,校正后的剩余不平衡量,以保证转子在动态时是在许用不平衡量的规定范围内,为动平衡又称双面平衡。
2、转子平衡的选择与确定如何选择转子的平衡方式,是一个关键问题。
其选择有这样一个原则:只要满足于转子平衡后用途需要的前提下,能做静平衡的,则不要做动平衡,能做动平衡的,则不要做静动平衡。
原因很简单,静平衡要比动平衡容易做,动平衡要比静动平衡容易做,省功、省力、省费用。
那么如何进行转子平衡型式的确定呢?需要从以下几个因素和依据来确定:1)转子的几何形状、结构尺寸,特别是转子的直径D与转子的两校正面间的距离尺寸b之比值,以及转子的支撑间距等。
2)转子的工作转速。
3)有关转子平衡技术要求的技术标准,如GB3215、API610第八版、GB9239和ISO1940等。
3、转子做静平衡的条件在GB9239-88平衡标准中,对刚性转子做静平衡的条件定义为:"如果盘状转子的支撑间距足够大并且旋转时盘状部位的轴向跳动很小,从而可忽略偶不平衡(动平衡),这时可用一个校正面校正不平衡即单面(静)平衡,对具体转子必须验证这些条件是否满足。
在对大量的某种类型的转子在一个平面上平衡后,就可求得最大的剩余偶不平衡量,并除以支撑距离。
如果在最不利的情况下这个值不大于许用剩余不平衡量的一半,则采用单面(静)平衡就足够了?quot;从这个定义中不难看出转子只做单面(静)平衡的条件主要有三个方面:一个是转子几何形状为盘状;一个是转子在平衡机上做平衡时的支撑间距要大;再一个是转子旋转时其校正面的端面跳动要很小。
对以上三个条件作如下说明:1)何谓盘状转子主要用转子的直径D与转子的两校正面间的距离尺寸b之比值来确定。
在API610第八版标准中规定D/b<6时,转子只做单面平衡就可以了;D/b≥6时可以作为转子是否为盘状转子的条件规定,但不能绝对化,因为转子做何种平衡还要考虑转子的工作转速。
转子找静平衡
转子找静平衡
一、转子静不平衡的表现
若将转子放置在静平衡台上, 然后用手轻轻转动转子, 让它自由停下来 , 可能出现下列情况 :
(1) 当转子的重心在旋转轴心线上时 , 转子转到任一角度都可以停下来 , 这时转子处于静平衡状态 , 这种平衡称为随遇平衡。
(2) 当转子的重心不在旋转轴心线上时 :
若转子承受的转动力矩大于轴和导轨之间的滚动摩擦力矩 , 则转子就要转动 , 使原有不平衡重量位于正下方 , 这种静不平衡称为显著不平衡。
若转动力矩小于滚动摩擦阻力矩 , 转子虽有转动趋势 , 但不能使不平衡重量转向正下方, 这种静不平衡称为不显著不平衡。
二、找静平衡前的准备工作
(1)静平衡台
转子找静平衡是在静平衡台上进行的 , 其结构如图 11-2 所示 , 轨道断面的形状
如图 11-3。
静平衡台的大小和其轨道工作面宽度α需根据转子的大小、轻重而定。
轨道
工作面宽度应保证轴颈和轨道工作面不被压伤 , 对于转子重量小于 l t 时 ,工作面宽度
为 3~6mm, 重量为 1~6t 时 , 工作面宽度为 6~30mm; 轨道的长度约为轴径的 6~8 倍 , 其材料通常采用碳案工具钢或钢轨制作。
轨道工作面应仔细地研磨或用磨床加工 , 其表
面粗糙皮不大于0.4/。
静平衡台安装后, 需对轨道进行校正 , 轨道水平方向的斜度不得大于 O.1~0.3mm/m, 两轨道间不平行度允许偏差为 2mm/m 。
静平衡台的安放位置应设在无机械振动和背风
的地方 , 以免影响转子找平衡的结果。
(2)转子
找静平衡的转子应清理干净 , 转子上的全部零件要组装好 , 并不得有松动。
轴颈的
椭圆度和圆锥度不应大于 0.05mm, 轴颈不许有明显的伤痕。
若采用假轴找静平衡时 , 假
轴与转子的自己合不得松动 , 假轴的加工精度不得低于原轴的精度。
转子放在轨道上时 , 动作要轻 , 轴的中心线要与轨道垂直 .
转子找静平衡的工作 , 一般是在转子和轴检修完毕后进行 , 在找完平衡后 , 转子
与轴不应再进行修理。
(3)试加重量
在找平衡时 , 需要在转子上配加临时平衡重量 , 称为试加重量。
试加重量较轻的
常用油泥 , 重的可用油泥加铅块。
若转子上有平衡槽或平衡孔、平衡柱的 , 则应在这
些装置上直接固定试加平衡块。
三、找静平衡方法
1. 两次加重法
两次加重法
只适用于显著不
平衡的转子找静
平衡。
具体作法
如下:
(1)找出转
子不平
衡重量
的方向
将转子放在静平衡台的轨道上 , 往复滚动数次 , 则重的一侧必然垂直向下 , 如数
次的结果均一致 , 即下方就是转子不平衡重量 G 的位置 , 定此点为 A。
A 点的对称方
向 ,即为试加平衡重量的位置 , 定该点为 B , 如图 1l-4( α〉所示 .
(2) 求第一次试加平衡重量
将 AB 转到水平位置 , 在OB方向加上一个重量 S, 加上这个重量后 , 要使 A 点能自由地从水平位置向下转一角度Θ ,Θ在 300~450之间为宜。
然后称出 S 的重量 , 再将 S 还回原位 , 如图11-4(b ) 所示。
(3) 求第二次试加平衡重量
仍将 AB 转到水平位置 ( 通常将 AB 调转 1800). 又在S 上增加一个重量 P, 要求加上 P 重量后 ,B 点能自由向下转动一个角度 , 这个角度必须和第一次的转动角度一
致。
然后取下P 称出其的重量 , 如图11-4(C ) 所示。
(4)计算应加平衡重量
两次转动所产生的力矩为 : 第一次是 Gx-Sr; 第二次是( S 十 P)r-Gx 。
因两次转
动角度相等 , 故这两次的转动力矩也相等。
在转动时导轨对轴颈的摩擦力矩, 因两次转动条件完全相同,其摩擦力矩也就相等,故在列等式时可略去不计。
若使转子达到平衡 , 所加的平衡重量 Q 应满足 Qr=Gx的要求。
将Qr代入(11-1)式 , 得 :
平衡重量 Q, 必须固定在试加重量的位置 , 若不能固定在原试加重量位置 , 则要通过力的平衡公式另行计算。
〈 5) 检验
将平衡重量 Q 固定并盘动转子 ,
让其自由停下 , 经多次盘功 , 若每次
序的位置都不相同 , 则说明显著不平
衡己经消除。
2. 试加重量法
试加重量法适用于不显著不平衡的
转子找静平衡。
具体作法如下 :
(1) 将转子分成若干等分 (6~12 等分均可 ), 并将各等分点标上序号 ,
〈 2) 将 1 点的半径线置于水平位置 , 并在 1 点上加上适当的重量S1 , 使转子向下转动一个小角度Θ, 然后取下称重。
用同样方法依次找出其它各点试加重量。
在加试加
重重时 , 必须使各点转动方向一致 , 加重的半径 r一致 , 转动的角度Θ一致如图ll-5( α ) 所示 .
(3) 以试加重量 S 为纵座标 , 加重位置的序号为横应标 , 绘出如图 11-5(b ) 所示曲线。
曲线的最低点就是转子不显著不平衡重量 G 的位置。
但要注意 : 曲线的最低点不一定与最小试加重量的位置相重合。
因为最小试加重量的位置是在转子编制的序号上 , 而曲线的最低点只是试加重量的两条曲线的交点。
曲线的最高点是转子最轻点 , 也就是平衡重量应加的位置 , 同样要注意这曲线的最高点与试加重量最重点的区别。
(4) 根据图 11 一 5 可得下列平衡式 :
若使转子达到平衡,所加的平衡重量 Q 应满足 Qr=Gx 的要求。
将 Qr代人 (11-3 〉式,得
把计算出的平衡重量Q 加在曲线的最高点。
曲线的最高点往往是一段小弧 , 高点不明显 , 为了取得较佳的平衡效果 , 可在转子与曲线最高点相应位置的左右作几次平衡试验 , 求得最佳的加重位置。
3. 秒表法
秒表法找平衡的原理 : 一个不平衡转子放在静平衡台上 , 由于不平衡重量的作用 , 使转子在轨道上来回摆动。
转子的摆动周期与不平衡重量有关 , 不平衡重量越大 , 转子的摆动周期越短 , 反之周期越长。
用秒表测出转子各点的摆动周期 , 根据各点不同的摆动周期 , 通过绘图和计算即可求出转子不平衡重量的位置与大小。
其方法如下 :
(1)确定转子不平衡重量的位置
把转子分成若干等份( 一般为 8 等分 ), 选择一个试加重量 S , 依次加在半径相等的各等分点上。
每个等分点加上试加重量后就置于水平位置 ,然后放手让转子在轨道上来回自由摆动 , 直到停止 , 并用秒表测出摆动一个周期所需的时间。
当试加重量 S 和不平衡重量 G 重合时,转子总不平衡重量为 S 十C,因为不平衡重量的加大 , 转子更易摆动 , 同时摆动一个周期所需要的时间最短 , 以 t 表示最小周期 ; 当 S 加在 G 的对方时 , 转子的不平衡重量为 S -G,此时摆动一个周期所需的时间最长 , 以 T 表示最
大周期。
根据每点的摆动周期数绘制曲线图 , 如图 11-6所示。
不平衡重量的位置 , 于曲线最低点 , 因此这点是不平衡重量与试加重量的重合点。
平重量则应力日在曲线的最高点。
(2)确定转子不平衡重量的大小
转子在轨道上的摆动周期和不平衡重量的关系 ,根据数学分析和实验得出 : 不平衡
重量 G 与摆动周期tx的平方成反比。
即 :
式中B一一比例常数。
当试加重量 S 和不平衡重量 G 重合时 , 得 S +H, 如将 S+G 和最小周期 t 写成式 (11-5) 的形式 , 得 :
式中B’一一比例常数。
当S 和G 的方向相反时,转子不平衡重量为:S-G, 如将S-G与T也写成(11一5)的形式 ,
可得 :
〈11-6) 式除以 (11 一 7) 式 , 得 :
四、剩余不平衡重量的测定和静平衡质量的评定
转子在找好显著不平衡和不显著不平衡后, 往往还存在着轻微的不平衡现象 , 这种轻微的不平衡称为剩余不平衡。
找剩余不平衡的方法与用试加重量法找转子不显著不平衡的方法完全一样。
通过测试得出转子各等分点中的一对差值最大的数值 , 用大值减去小值之差除以 2, 其得数就是剩余不平衡重量。
剩余不平衡重量越小 , 静平衡的质量越高。
实践证明 : 转子找静平衡后剩余不平衡重量在额定转速下所产生的离心力不超过该转子重力的 5% 时 , 可以保证机组平稳地运行 , 即静平衡已经合格。
精品资料
转子找静平衡
一、转子静不平衡的表现
二、找静平衡前的准备工作
三、找静平衡方法
四、剩余不平衡重量的测定和静平衡质量的评定仅供学习与交流,如有侵权请联系网站删除谢谢11。