幻方小报

9格幻方的小技巧
1. 嘿，你知道吗，填 9 格幻方有个超棒的小技巧！比如在填数字的时候，先找到中间那个格子，把中间数填进去，这就像给整个幻方找到了中心呀！像 1 到 9 来填，把 5 填在中间。

2. 哇哦，还有一个很有用的哦！从最小的数字开始，按照一定顺序去填，这就像排着队一个一个来，多有序啊！比如依次从左上角开始填。

3. 嘿呀，注意啦！每行每列的数字之和要是一样的哦，这可不能马虎。

就好比是一群小伙伴，大家的实力都要差不多才行呢！比如填好后检查一下是不是每行每列的和都相等。

4. 哎呀呀，把数字对称着填也很不错哦！这就像照镜子一样，两边是一样的，多有意思！像左上角和右下角的数字可以对称着来填。

5. 嘿，填的时候要大胆尝试呀！别害怕错，就像冒险家一样去探索。

比如填一个数字感觉不太对，那咱就换个试试。

6. 哇，注意数字的奇偶性搭配哟！这就像跳舞的时候男女搭配一样重要呢！比如奇数和偶数合理分布。

7. 哈哈，最后别忘了整体检查一遍呀！这就像考试完检查试卷一样重要呢！看看有没有填错的地方。

我觉得呀，这些小技巧能让填 9 格幻方变得更有趣，也更容易，大家
赶紧去试试吧！。

1.五年级奥数幻方（一）学生版2.了解偶数阶幻方相关知识点3.深入学习三阶幻方一、幻方起源也叫纵横图,也就是把数字纵横排列成正方形,因此纵横图又叫幻方．幻方起源于我国,古人还为它编撰了一些神话．传说在大禹治水的年代,陕西的洛水经常大肆泛滥,无论怎样祭祀河神都无济于事,每年人们摆好祭品之后,河中都会爬出一只大乌龟,乌龟壳有九大块,横着数是3行,竖着数是3列,每块乌龟壳上都有几个点点,正好凑成1至9的数字,可是谁也弄不清这些小点点是什么意思．一次,大乌龟又从河里爬上来,一个看热闹的小孩惊叫起来：“瞧多有趣啊,这些点点不论横着加、竖着加还是斜着加,结果都等于十五！”于是人们赶紧把十五份祭品献给河神,说来也怪,河水果然从此不再泛滥了．这个神奇的图案叫做“幻方”,由于它有3行3列,所以叫做“三阶幻方”,这个相等的和叫做“幻和”．“洛书”就是幻和为15的三阶幻方．如下图：987654321我国北周时期的数学家甄鸾在《算数记遗》里有一段注解：“九宫者,二四为肩,六八为足,左三右七,戴九履一,五居中央．”这段文字说明了九个数字的排列情况,可见幻方在我国历史悠久．三阶幻方又叫做九宫图,九宫图的幻方民间歌谣是这样的：“四海三山八仙洞,九龙五子一枝连；二七六郎赏月半,周围十五月团圆．”幻方的种类还很多,这节课我们将学习认识了解它们．二、幻方定义幻方是指横行、竖列、对角线上数的和都相等的数的方阵,具有这一性质的33⨯的数阵称作三阶幻方,44⨯的数阵称作四阶幻方,55⨯的称作五阶幻方……如图为三阶幻方、四阶幻方的标准式样,知识点拨教学目标5-1-4-1.幻方（一）98765432113414151612978105113216三、解决这幻方常用的方法⑴适用于所有奇数阶幻方的填法有罗伯法．口诀是：一居上行正中央,后数依次右上连．上出框时往下填,右出框时往左填．排重便在下格填,右上排重一个样．⑵适用于三阶幻方的三大法则有： ①求幻和： 所有数的和÷行数（或列数）②求中心数：我们把幻方中对角线交点的数叫“中心数”,中心数＝幻和÷3． ③角上的数=与它不同行、不同列、不同对角线的两数和÷2．四、数独数独简介：（日语：数独 すうどく）是一种源自18世纪末的瑞士,后在美国发展、并在日本得以发扬光大的数学智力拼图游戏。

49 2 35 7 8 16
4、如何改变幻方：
改变数的位置还有可能满足上述规律吗？
4 92 357 816
8 16 357 492
2 94 753 618
6 18 753 294
上下换 左右换 上下左右换
4、探究改变幻方的规律： 共有8种：
4 92 357 816
83
59 2
618 7 53 2 94
276+951+438= 1665 672+159+834= 1665
2762+9512+438=2 1172421 6722+1592+8342= 1172421
4）每列看成的三位数和 =它逆转之后的三位数。
5）每列看成的三位数的平方和 =它逆转之后的三位数平方和
行也成立
3、探究幻方的规律（3）：
百子回归碑是一部 百年澳门简史，可 查阅四百年来澳门 沧桑巨变的重大历 史事件以及有关史 地、人文资料等。
中间两列上部（系十九
世纪）：“ 1887 ” 年《中葡条约》正式 签署，从此成为葡人 上百年（距今 100 余 13 年）“永久管理澳 门”的法律依据。又 如中间两列下部（系 二十世纪）：“ 49 ” 年中华人民公和国成 立，从此中国人民站 起来了；“ 97 ”年香 港回归祖国。
3接跟5+下a2有3来+3关你=1的们9+有看b+哪看25些幻行和b=, 17
35 5
能哪幻求些和出列=5来或+2吗哪3+?些15对+2角9=线74?
11 23
17
幻a=和74-不(35能+2求3+出3)=来13 ….
19 1b7 a 25 3 但可以表示出来:

64 3678 120 92 134 50 10622 19 15 21 2 13 9 17 23 25 16 8 4 1 22 14 10 5 6 12 18 20 7 11 24 19 15 2 23 25 16 8 4 1 22 14 10 6 12 18 19 15 21 2 13 9 25 168 1 2214 20 7 319 15 2 25 16 8 1 2214 3 A B C D1 234 5 67 89 ⑵ ⑴ 8 6 1 3 75 4 29 56幻方又叫魔方、九宫算或纵横图，它起源于我国上古时代，是一种具有奇妙性质的数字表格．一般地，在n ×n （n 行n 列）的方格里，既不重复也不遗漏地填上n ×n 个连续的自然数（注意，这n ×n 个连续自然数不一定要从1开始），每个数占1格，并使每一行、每一列以及两条对角线上的几个自然数的和都相等，这样排列成的数字图形叫做n 阶幻方（标准幻方）．其中，相等的和叫做幻和，n 叫做阶．幻和＝幻方内所有数字之和÷阶数，奇数阶幻方的中心数＝幻和÷阶数．非标准的幻方不限于连续自然数，右图所示即为一个非标准的三阶幻方．幻方分为奇数阶幻方和偶数阶幻方．偶数阶幻方又分双偶数阶幻方和单偶数阶幻方（4K 型的数叫做双偶数，4K ＋2型的数叫做单偶数）．幻方具有对称性．如下图的四阶幻方就具有丰富多彩的对称性．同一曲线所串连的四个数的和都相等，并且和每行、每列、两条对角线上四个数的和相等，都等于这个幻方的幻和．这就是幻方的对称性．幻方具有轮换性．如右图所示的幻方，可以看成是先将五阶幻方的前三行移到下面，再把移动后的左边的三列移到右边以后得到的（反过来移动也行）．这样，随你怎样选取5×5的一个方块后必然得到一个五阶幻方，这就是幻方的轮换性． 幻方的构造方法： 1．奇数阶幻方的构造方法：⑴ 杨辉三阶幻方构造法：我国古代著名数学家杨辉在《续古摘奇算法》中介绍的一种排法，它可以简单地归纳为四句话：“九子斜排，上下对易，左右相更，四维挺出”．“九子斜排”，即以右图中A 、B 、C 、D 任一处为起点，按照从小到大的顺序和确定的方向（图中以A 处为起点，从向右向下方向），将1～9这九个数依次斜排；“上下对易，左右相更”，即将A 处与C 处，B 处与D 处的两个数位置互换；“四维挺出”，即将四边中间的数移到各自箭头所批的位置．这样，一个三阶幻方就编排完了．训练⑴① 用从1开始的连续自然数组成一个十阶幻方，其幻和是多少？② 用“杨辉三阶幻方构造法”及3～11编排一个三阶幻方，填入右图中．③ 如右图⑴的3×3的阵列中填入1～9九个自然数，构成了我们熟知的三阶幻方．现有一个3×3的阵列如右图⑵，请选择九个不同的自然数填入这九个方格中，使得其中最大数为20，最小数大于5，而且每一行、每一列及每条对角线上的三个数的和都相等．④ 请编出一个三阶幻方，使其幻和为24，填入右图中．⑤ 如右图所示，在3×3的阵列中，第一行第三列的位置上填5，第二行第一列的位置上填6，请你在空格中填上适当的数，使方阵的行、列、对角线上的三个数之和均为36． ⑥ 把3、4、5、8、9、10、13、14、15编排一个三阶幻方，其幻和是多少？14 11 61 8 7 151012 1332 4 5 9 16 14 11 61 8 7 151012 13 3 245 9 16 14 11 61 87 151012 13 3 2 4 5 9 16 14 11 618 7 151012 13 3 24 5 9 1614 11 61 8 7 151012 13 3 2 4 5 9 16 14 11 61 8 7 151012 13 3 2 4 5 9 16 ⑴ ⑵ ⑶ ⑷ ⑸ ⑹4 ⑺ 将九个连续自然数填人右图中三行三列的九个方格中，使每一横行、每一竖列及每一条对角线上的三个数之和都等于51．⑻ 在右图中的空格中填入不大于18而且互不相同的偶数（其中已填好一个数），使每行、每列和对角线上三个数之和都等于30．⑼ 把1～9这九个数字填入3×3的方格中，这样，每一行的三个数字组成一个三位数，如果要使第二行的三位数是第一行的2倍，第三行的三位数是第一行的3倍，应怎样填数？⑽ 诸葛亮只有360名士兵，全部驻守在城上，为了迷惑敌人，不论从哪一面观察，都有100名全副武装的士兵守城（如下图所示）．为了打退敌人的围攻，诸葛亮决定抽调一些士兵突袭敌人，并且不论从哪一面看士兵反而增加了25名，试填出兵力分布图，并求出抽调了多少名士兵？⑵ 罗伯法（用于编排奇数阶连续自然数幻方）：这是由法国人罗伯总结出的构造奇数阶连续自然数幻方的简单易行的方法．具体方法如下：先把1（或最小的数）放在第一行正中；然后按以下规律排列剩下的12 n 个数：① 每一个数放在前一个数的右上一格； ② 如果这个数所要放的格已经超出了顶行那么就把它放在底行，仍然要放在右一列； ③ 如果这个数所要放的格已经超出了最右列那么就把它放在最左列，仍然要放在上一行； ④ 如果这个数所要放的格已经超出了顶行且超出了最右列那么就把它放在前一个数的下一行同一列的格内； ⑤ 如果这个数所要放的格已经有数填入，处理方法同④．根据这个规则，可以编一个编排奇数阶连续自然数幻方的口诀：㈠ 横向叫行竖叫列，从1开始连续写，1写首行下中间，右列沉底将2写；㈡ 数顺右上方向走，碰到边框猛回头，上行最左写后数，再沿右上方向走； ㈢ 若碰有数下一格，方向不变继续走，碰顶向右掉到底，再按前面规则走。

8 34 1 59 672
492 35 7 816
将这个幻方分别顺时针旋转三次
492 357 816
它们有什 么共同的 特点吗？
和为15的幻方的特征
• 中心数都是5 • 四个角上都是双数 • 每边的中间都是单数 • “米”字线上相对的两个端点数的和为10
二四为肩，六八为足，左三右七，戴九履一， 五居中央。
第一关
①
闯关游戏
②
③
第二关 这些乌龟上的图案已经看不清了，你能帮它们
找回原来的数字吗？（幻方的和为15）
先填哪里的 空格呢？
1 5 97
6 59 1
3 8
第三关
趣味题
将合适的数（1~9，不重复）填入下图， 使每条线上3个数的和与中间标出的数相 等。
65 4
62 14
你真棒！
•
1.批评对作品的意义不言而喻。好的 批评如 同灯光 ，指引 着作品 从暗处 走向前 台。近 些年的 诗歌批 评中， 不乏这 样的经 典或中 肯之作 。
亲爱的同பைடு நூலகம்们，再见！
•
7.诗歌批评庸俗化趋势亟须扭转。文 学批评 的职业 公信力 需要树 立，批 评家需 要贡献 学术良 知。果 真如此 ，对诗 歌和读 者，都 将是福 音。
•
8.中国音乐在发展过程中，不断承传 自我， 吸收各 地音乐 ，器乐 发达， 演奏形 式丰富 。金、 石、土 、革、 丝、木 、匏、 竹，皆 可作乐 器。乐 曲类型 已有祭 神乐、 宴乐、 军乐、 节庆乐 等区别 。玄宗 时已有 超百人 的大型 交响乐 团，其 演员按 艺术水 平分为 “坐部 伎”与 “立部 伎”。
•
5.一切表现形式都应该是创造的成果 。今天 的浪漫 或许是 明天的 现实， 当下的 现实也 可能是 昨天的 浪漫。 重要的 是我们 的作品 是否揭 示生命 本质， 精神是 否向真 向善向 上，以 及手上 的“主 义”是 否与我 们的诉 求达成 一致。

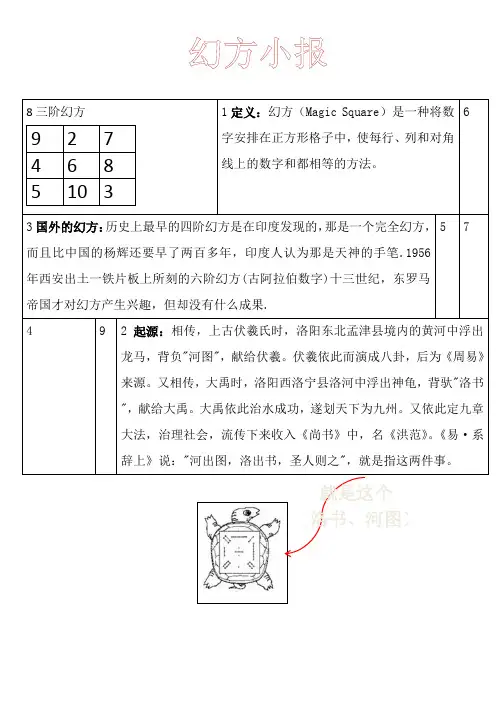
8三阶幻方
9 2 7
4 6 8
5 10 3 1定义：幻方（Magic Square）是一种将数
字安排在正方形格子中，使每行、列和对角
线上的数字和都相等的方法。

6
3国外的幻方：历史上最早的四阶幻方是在印度发现的，那是一个完全幻方，
而且比中国的杨辉还要早了两百多年，印度人认为那是天神的手笔.1956
年西安出土一铁片板上所刻的六阶幻方(古阿拉伯数字)十三世纪，东罗马
帝国才对幻方产生兴趣，但却没有什么成果.
57
492起源：相传，上古伏羲氏时，洛阳东北孟津县境内的黄河中浮出龙马，背负"河图"，献给伏羲。

伏羲依此而演成八卦，后为《周易》
来源。

又相传，大禹时，洛阳西洛宁县洛河中浮出神龟，背驮"洛书
"，献给大禹。

大禹依此治水成功，遂划天下为九州。

又依此定九章
大法，治理社会，流传下来收入《尚书》中，名《洪范》。

《易·系
辞上》说："河出图，洛出书，圣人则之"，就是指这两件事。

就是这个
（洛书、河图）。

初一数学幻方的历史与解法数学小报初一数学幻方的历史与解法幻方是指由n × n的方阵组成，其中每个格子都填入了不同的数字，使得每行、每列和对角线的数字之和都相等。

幻方具有神秘而吸引人的特性，不仅在数学中被广泛研究，还被认为拥有一定的神秘力量。

幻方的历史可以追溯到中国古代。

早在公元650年左右，中国古代数学家杨辉就研究过幻方的特性和构造方法，他发现了一些特殊的幻方，如"阶四幻方"和"边三幻方"。

这些幻方除了满足基本的行、列和对角线之和相等的条件外，还具有一些独特的特点。

欧洲的数学家们也对幻方产生了浓厚的兴趣。

在16世纪，德国数学家冯·冯西特尔和法国数学家达德尼分别提出了一种构造幻方的方法，被称为"杨辉三角法"和"达德尼方法"。

这些方法可以通过一定的规则来构造出各种不同阶数的幻方。

在近代，科学家们开始运用更先进的技术来研究幻方。

通过计算机的帮助，他们发现了许多新奇的幻方，如"庞加莱幻方"和"帕斯卡幻方"。

这些幻方不仅满足基本的条件，还具有更多的特殊性质，如旋转对称、变换对称等。

解决幻方的方法有很多种。

最常见的方法是通过数学推理和试错来找出合适的数字填入每个格子中。

另外，还可以利用一些特殊的技巧和规律来简化解题过程。

例如，对于奇数阶的幻方，可以利用杨辉三角法和达德尼方法来构造；对于偶数阶的幻方，可以利用调整法和变换方法来生成。

总的来说，幻方是一门充满魅力和挑战的数学课题。

它不仅展示了数学的美妙和深刻，还激发了人们对数学的兴趣和研究欲望。

无论是古代还是现代，数学家们都在不断探索和创造新的幻方，为这个神秘的数学世界增添了更多的色彩和魅力。

幻方（一）李明亮幻方是我国古代研究的算术内容之一，在中国，至少已有两千多年的历史了。

它最早被称为“洛书”（就是三行幻方）。

据说，大禹治水时，在洛水看到一只神龟背上有奇特的图案，这就是“洛书”——《周易》称：“河出图，洛出书。

”幻方就是由“洛书”与“河图”发展而来的。

在甄鸾（公元六世纪北周人）注的《数术记遗》一书中，称幻方为“九宫算”。

南宋的杨辉把幻方叫做“纵横图”，并对幻方进行了深入的研究，例如，他构造三行幻方的方法是：“九子斜排，上下对易，左右相更，四维挺出，戴九履一，左三右七，二四为肩，六八为足。

”他还进一步研制出了四至十行的幻方。

在幻方里，每一横行（以下简称行）、每一竖行（以下简称列）、每一对角线上的数的和都相等。

我们把幻方中的这个相等的和称为幻方定数。

组成幻方的数一般是等差数列（按顺序排列的一列数，每相邻的两个数的差都相等）。

如用1、3、5、……15、17这九个数可以制成一个三行幻方。

把n2个数按一定的顺序排成n行n列的方阵，如果每一行、每一行、每一对角线上的数都成等差数列，那么，用这n2个数就可以制成n行幻方。

如用2、4、6，9、11、13，16、18、20也可以制成三行幻方。

一、幻方的制法（一）行数为奇数的幻方的制法（以七行幻方为例）１．选1、2、3、……49这４９个数，把它们按顺序排成７行７列的斜方阵。

排好后，在中间画一个正方形（以中间数２５为中心），使斜方阵中间行（22、23、24、25、26、27、28这一行）和中间列（4、11、18、25、32、39、46这一列）的数都正好落在正方形的对角线上；再把这个正方形平均分成４９个方格，其中２４个是空方格（制n行幻方时，有（n2－１）÷2个空方格）。

如图２．２．把正方形外面的数填入空格。

每个数都填入它所在行或所在列中离它最远的空格中；同一行或同一列中，如果正方形外面有两个或两个以上的数，就先填靠近正方形的数，如先填9和41，后填1和49。

幻பைடு நூலகம்初一七班 尤佳琪
一、定义。
在一个由若干个排列整齐的数组成的正方形中，图中任意一横行、一纵行及对角线的几个数之和都相等，具有这种性质的图表，称为“幻方”。我国古代称为“河图”、“洛书”，又叫“纵横图”。n阶幻方是由前N2个自然数组成的一个n阶方阵，其各行、各列及两条对角线所含的n个数的和相等的图形叫幻方。
二、幻方的历史。
关于幻方的起源，中国有“河图”和“洛书”之说。相传在远古时期，伏羲氏取得天下，把国家治理得井井有条，感动了上花于是黄河中跃出一匹龙马，背上驮着一张图，反作为礼物献给他，这就是“河图”，了是最早的幻方伏羲氏赁借着“河图”而演绎出了八卦，后来大禹治洪水时，咯水中浮出一只大乌龟，它的背上有图有字，人们称之为“洛书”。“洛书”所画的衅中共有黑、白圆圈45个。把这些连在一起的小圆和数目表示出来，得到九个。这九个数就可以组成一个纵横图，人们把由九个数3行3列的幻方称为3阶幻方，除此之外，还有4阶、5阶...

没法，组合数学还考幻方构造。

这东西不看解法真不会写，虽然没见有啥用，但还是记录下，免得日后再找。

按目前填写幻方的方法，是把幻方分成了三类，即奇数阶幻方、双偶阶幻方、单偶阶幻方。

下面按这三类幻方，列出最常用解法（考试用，不求强大，只求有效！）。

奇数阶幻方（罗伯法）奇数阶幻方最经典的填法是罗伯法。

填写的方法是：把1（或最小的数）放在第一行正中；按以下规律排列剩下的(n×n－1)个数：1、每一个数放在前一个数的右上一格；2、如果这个数所要放的格已经超出了顶行那么就把它放在底行，仍然要放在右一列；3、如果这个数所要放的格已经超出了最右列那么就把它放在最左列，仍然要放在上一行；4、如果这个数所要放的格已经超出了顶行且超出了最右列，那么就把它放在前一个数的下一行同一列的格内；5、如果这个数所要放的格已经有数填入，那么就把它放在前一个数的下一行同一列的格内。

例，用该填法获得的5阶幻方：17241815235714164613202210121921311182529双偶数阶幻方（对称交换法）所谓双偶阶幻方就是当n可以被4整除时的偶阶幻方，即4K阶幻方。

在说解法之前我们先说明一个“互补数”定义：就是在 n 阶幻方中，如果两个数的和等于幻方中最大的数与 1 的和（即n×n＋1），我们称它们为一对互补数。

如在三阶幻方中，每一对和为 10 的数，是一对互补数；在四阶幻方中，每一对和为 17 的数，是一对互补数。

双偶数阶幻方的对称交换解法：先看看4阶幻方的填法：将数字从左到右、从上到下按顺序填写：12345678910111213141516内外四个角对角上互补的数相易，（方阵分为两个正方形，外大内小，然后把大正方形的四个对角上的数字对换，小正方形四个对角上的数字对换）即（1，16）（4，13）互换（6，11）（7，10）互换即可。

16231351110897612414151对于n=4k阶幻方，我们先把数字按顺序填写。

里，使之成为幻方.
2.在下列各图的空格里，填上合适的数，使横行、竖列及两
条对角线上三个数的和都相等.
438
六、拓展
1.将5个2和4个-2这九个数填入3×3的方格里，使得每行、每列、 两条对角线的三个数的乘积都是8. 2.将 12，11 ，10 ，9 ，8 ，7 ，6 ，5 ， 4，3 ，2 ，1 ， 0 ， -1，-2 ，-3 ，-4 ，-5 ，-6 ，-7 ，-8 ，-9 ， -10，
九子斜排
9
3
7
1
九子斜排 上下对易 左右更替 四维挺出
1.请把9个数字 6, 5, 4, 3, 2, 1, 0，-1，-2 填
在3×3的方格中构成三阶幻方.
-2 -1 6 1 0 4 20 4
阶梯法步骤： 1.排序， 2.画图，
3 -2 5
3.斜排， 4.归位.
6
2、请把9个数字 -8, 8 , -6，6 -4, 4，-2, 0, 2,
294 753 618
三、幻方的应用
数独是一种数学游戏。玩 家需要根据9×9盘面上的已知 数字，推理出所有剩余空格的 数字，并满足每一行、每一列 、每一个粗线宫（3×3）内的 数字均含1-9，不重复.
数独游戏
45
19 99 12 20
97 49
8 16 357 49 2
③
读书人生
八科一生学六回， 三书五经读七春； 四年九创书二本， 读书人生奏强音 .
-11，-12这25个数分别填入6×6的方格中，构成五阶幻方．
只要你在路上，就不要放弃前进的勇气，走走停停的生活会一直继续。 如果为了安全而不和大海在一起，船就失去了存在的意义。 这个世界并不在乎你的自尊，只在乎你做出来的成绩，然后再去强调你的感受。 命是弱者的借口，运是强者的谦辞，辉煌肯定有，就看怎么走。 为了你，很多事我不一定会，但我在努力学。 年轻是我们唯一拥有权利去编织梦想的时光。 受惠的人，必须把那恩惠常藏心底，但是施恩的人则不可记住它。--西塞罗 人生道路，绝大多数人，绝大多数时候，人都只能靠自己。 世上的事就是这样：只要你以积极的态度，勇敢的面对，脚踏实地的努力奋斗，成功就会与你如影随形！我渴望你能成功！——李慎奇 过去不等于未来。 当无事时，应该像有事那样谨慎，当有事时，应像无事时那样镇静。因为漫长的旅途中，实在难以完全避免崎岖和坎坷。 路漫漫其修道远，吾将上下而求索。——屈原

泛对角线幻方
将数字按照一定的规律填 充到格子中，使得每条泛 对角线上的数字之和相等。
正交幻方
将数字按照一定的规律填 充到格子中，使得每条正 交线上的数字之和相等。
03 幻方的数学原理
数学基础
代数基础
幻方是在一定规则下，将数字填 入一个正方形网格中，每个数字 代表一个坐标，通过代数运算找
出对应的数字。
04 幻方的应用与拓展
幻方在游戏中的应用
数独
这是一种基于幻方原理的数字游戏，玩家需要将数字1-9填入一个3x3的格子中， 使得每行、每列以及每个3x3的子格中都包含这9个数字。
棋盘游戏
一些棋盘游戏如井字游戏（Tic Tac Toe）和连珠（Gomoku）也可以视为幻方 在游戏中的应用，玩家需要在棋盘上放置棋子，使得满足特定的排列规则。
趣味数学-幻方
目录
• 幻方简介 • 制作幻方的方法 • 幻方的数学原理 • 幻方的应用与拓展 • 趣味数学与幻方
01 幻方简介
幻方的定义
01
幻方是一种将数字、图形或符号 按照特定规则排列在正方形网格 中的数学游戏。
02
幻方要求每一行、每一列以及对 角线上的数字或符号之和都相等 ，或者遵循特定的数学关系。
偶数阶幻方的构造公式
将n阶幻方看作是一个n×n的矩阵，矩 阵中的元素可以用坐标表示，通过代数 运算和矩阵变换，可以得出偶数阶幻方 的构造公式。
幻方的数学证明
奇数阶幻方的。
偶数阶幻方的证明
通过数学归纳法和代数运算，可 以证明偶数阶幻方的构造方法是 正确的。
幻方的历史与起源
幻方最早可以追溯到中国的洛书， 据传为黄帝时期的大臣洛所创。
在中世纪，幻方逐渐传播到欧洲， 成为数学家和哲学家们研究的对

另一种构造奇数阶幻方的方法是利用杨辉三角。将1放在第一 行中间，然后利用杨辉三角的规律，将其它数字填入，同样 保证每个数字都不重复。
偶数阶幻方的构造方法
偶数阶幻方中最常用的是四阶和八阶幻方。四阶幻方的构 造方法是将1放在第一行中间，然后按顺序将其它数字填入 ，每行从左到右填入数字，每列也从左到右填入数字，保 证每个数字都不重复。
单人幻方游戏
九宫格幻方
将1至9的数字填入3x3的九宫格中，使得每行、每 列以及对角线的数字之和都相等。
16格幻方
将数字1至16填入4x4的方格中，使得每行、每列 、两条对角线以及四个角落的数字之和都相等。
25格幻方
将数字1至25填入5x5的方格中，使得每行、每列 、两条对角线以及四个角落的数字之和都相等。
奇数阶幻方
由奇数个数字组成的幻方，通常为3×3、5×5等。这类幻 方构造相对简单，但也有一定的难度。
偶数阶幻方
由偶数个数字组成的幻方，如4×4、6×6等。这类幻方构 造较为复杂，需要遵循一定的规律和技巧。
广义幻方
不仅限于数字，还可以用字母、符号等代替数字，甚至可 以是非线性的矩阵。这类幻方更加灵活多变，具有更广泛 的用途。数学中的规律美 Nhomakorabea规律之美
幻方中的数字按照一定的规律排 列，这种规律美是数学中非常重
要的美学特征之一。
逻辑之美
幻方的构造过程需要遵循一定的 逻辑，这种逻辑美也是数学中非
常重要的美学特征之一。
统一之美
幻方中的数字虽然千变万化，但 都遵循着统一的规律和逻辑，这 种统一美也是数学中非常重要的
美学特征之一。
数学中的逻辑美
多人幻方挑战赛
团队赛
01
多个团队同时进行幻方挑战，以最快完成且符合规则的团队为