423拉普拉斯变换的收敛域讲解

第四章 拉普拉斯变换分析1．拉普拉斯收敛域的意义是什么？拉普拉斯变换定义为：()()st X s x t e dt ∞--∞=⎰ 是广义积分，其中变量s j σω=+是复变量，因而积分是否存在将取决于变量s ， 那么使得广义积分存在的s 的值所组成的集合就是拉氏变换的定义域。

这说明，拉氏变换的收敛域确定了拉氏变换存在范围。

收敛域不同，说明信号不同。

对于单边拉变换来说，其收敛域的一般形式为0σσ>。

2．极点和零点的意义是什么？它们有什么作用？如果 l i m ()s pX s →=∞， 则称s p =是()X s 的极点； 如果 l i m ()0s zX s →=， 则称s z =是()X s 的零点。

极点的位置决定了信号波形变化参数，如单调性（增长或衰减）和振荡快慢（频率）；而零点确定了信号波形的不变参数，如振幅和初相位。

3．拉普拉斯变换的初值定理和终值定理的应用条件是什么？拉普拉斯变换的初值定理为：若 () (f t F s ↔， 且()f t 连续可导 则 0l i m ()(0)l i m ()s t f t f s F s ++→∞→== 其应用的条件为()F s 必须是有理真分式； 如果不是，则必须利用长除法，将()F s 表示为 ： 0()()()F s B s F s =+ 其中，B (s )是s 的多项式，0()F s 是有理真分式。

则有000lim ()(0)(0)lim ()s t f t f f sF s +++→∞→=== 拉普拉斯变换的终值定理为：若 () (f t F s ↔， 且()f t 连续可导 则 0l i m ()()l i m ()t s f t f sFs →∞→=∞=由于我们只讨论单边拉氏变换，因而其应用的条件为()F s 的极点必须全部在s 平面的左半平面，否则，其终值不存在。

4．如何获得电容或电感元件的等效电路？根据电容和电感的伏安特性以及拉氏变换的微分积分性质，可以很方便地获得两种元件的s 域等效电路。

拉普拉斯变换域1. 引言拉普拉斯变换是一种在信号处理和控制系统中广泛应用的数学工具。

通过将时间域中的函数转换为复平面上的频率域表示，可以更方便地分析和处理信号。

拉普拉斯变换在电路分析、控制理论、通信系统等领域都有重要的应用。

本文将介绍拉普拉斯变换的基本概念、性质以及在信号处理中的应用。

首先，我们将介绍拉普拉斯变换的定义和数学表达式。

然后，我们将讨论拉普拉斯变换的性质，包括线性性、时移性、尺度变换等。

最后，我们将介绍一些常见的信号处理问题，并展示如何利用拉普拉斯变换来解决这些问题。

2. 拉普拉斯变换定义对于一个定义在实数域上的函数f(t)，其拉普拉斯变换可以通过以下积分来定义：F(s)=∫e−st∞f(t)dt其中，s是复平面上的一个复数。

3. 拉普拉斯变换性质3.1 线性性对于任意常数a和b，以及两个函数f(t)和g(t)，有以下线性性质成立：L(af(t)+bg(t))=aF(s)+bG(s)其中，F(s)和G(s)分别是f(t)和g(t)的拉普拉斯变换。

3.2 时移性如果对于一个函数f(t)，其拉普拉斯变换为F(s)，那么对于任意常数a，有以下时移性质成立：L(e at f(t))=F(s−a)3.3 尺度变换如果对于一个函数f(at)，其拉普拉斯变换为F(s)，那么对于任意常数b，有以下尺度变换性质成立：L(f(bt))=1bF(sb)3.4 初值定理和终值定理初值定理和终值定理是拉普拉斯变换的两个重要性质。

初值定理指出：如果一个函数f(t)在t=0处连续，并且所有阶数的导数在t=0处存在有限值，那么其初始值可以通过以下公式得到：limsF(s)=f(0+)s→∞其中，f(0^+)表示函数f(t)在t=0+时刻的右极限。

终值定理指出：如果一个函数f(t)在t=0处连续，并且在t=0时刻的右极限存在有限值，那么其终值可以通过以下公式得到：sF(s)=f(∞)lims→0其中，f()表示函数f(t)在t=。

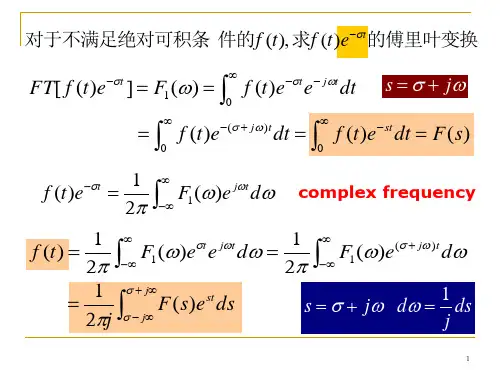
拉普拉斯变换　２．拉氏变换的收敛域与零极点图　拉氏变换的ROC 及零极点图　2()()()t tx t e u t e u t −−=+例３．　20()t stt stX s e e dt e e dt∞∞−−−−=+∫∫1(),1te u t s −↔+ Re[]1s >−21(),2te u t s −↔+Re[]2s >−1−σωj 2−σωj 定义：使拉氏变换积分收敛的那些复数　ｓ　的集合，称为拉氏变换的收敛域（ROC ）　。

　可见：拉氏变换的收敛域是各个收敛域的公共部分。

ＲＯＣ总是以平行于 轴的直线作为边界的，边界的位置总是与 的分母的根相对应的。

　j ω()X s Re[]1s >−σωj 2−1−21123(),1232s X s s s s s +∴=+=++++ 分子多项式的根称为零点，分母多项式的根称为极点。

　 将 的全部零点和极点表示在Ｓ平面上，就构成了零极点图。

零极点图及其收敛域可以表示一个 ，最多与真实的 相差一个常数因子 。

　()X s ()X s ()X s M 因此，零极点图是拉氏变换的图示方法。

　若 是有理函数　()X s ()()()()()iiiis N s X s MD s s βα−==−∏∏零极点图　·可以归纳出ROC 的以下性质：　j ω３．右边信号的ROC 位于Ｓ平面内一条平行于 轴的直线的右边。

　５．时限信号的ROC 是整个　Ｓ　平面。

　２．在ROC 内无任何极点。

　j ω１．ROC 是　Ｓ　平面上平行于 轴的带形区域。

　４．左边信号的ROC 位于Ｓ平面内一条平行于 轴的直线的左边。

　j ω６．双边信号的ROC 如果存在，一定是　Ｓ　平面内平行于 轴的带形区域。

　j ω()()0()1[1]T at stTs a ts a TX s e e dte dte s a−−−+−+==−+∫∫例４．　{()x t =ate−0其它　0t T <<t时限信号的ROC 是整个　Ｓ　平面。