第四章 图形变换——投影变换

初中数学知识归纳正交投影与投影变换的概念与计算正交投影与投影变换是初中数学中的重要理论知识。

本文将对这两个概念进行归纳，并介绍它们的计算方法。

一、正交投影的概念与计算正交投影是指将一个立体图形在某个平面上的投影。

具体而言，对于一个三维空间中的点P(x, y, z)，当它沿着某个法向量为n(a, b, c)的平面进行投影时，投影点P'的坐标可以通过以下计算方法得出：1. 计算投影向量的长度首先，需要计算投影向量的长度，即将平面法向量标准化。

设向量n的长度为d，即d = √(a^2 + b^2 + c^2)。

然后将a、b、c分别除以d，得到标准化后的法向量n'，即n' = (a/d, b/d, c/d)。

2. 计算投影点的坐标接下来，需要计算点P在平面上的投影点P'的坐标。

根据向量投影的原理，可以得到以下计算公式：P' = P - Proj_n(P) = P - (P·n')n'其中，Proj_n(P)表示点P在向量n'上的投影，P·n'表示点P与向量n'的数量积。

二、投影变换的概念与计算投影变换是指将一个二维图形通过某种变换映射到另一个平面上的过程。

在数学中，通常使用矩阵的乘法运算来表示投影变换。

设原平面上的点为P(x, y)，经过投影变换后的点为P'(x', y')，则有以下计算公式：x' = a*x + b*y + cy' = d*x + e*y + f其中，a、b、c、d、e、f为投影变换的参数，可以根据具体的变换要求进行确定。

这些参数可以表示平移、缩放、旋转等操作，从而实现对图形的不同变形效果。

三、实际应用举例正交投影和投影变换在几何学中应用广泛，下面以一些具体的应用举例说明：1. 工程制图在工程制图中，正交投影被广泛用于展示三维物体的平面图。

通过将三维物体沿着不同的方向进行投影，可以得到其俯视图、正视图、侧视图等平面图，便于工程师进行设计和分析。

图形变换基本概念图形变换是计算机图形学中的一个重要概念，它通过对图形进行特定操作来改变其形状、大小或位置。

图形变换常用于图像处理、动画制作和计算机图形学等领域，对于实现图像变换效果有着重要的作用。

本文将介绍几种常见的图形变换方法及其基本概念。

一、平移变换（Translation）平移变换是一种基本的图形变换方法，它将图形沿着指定的方向进行移动。

平移变换可以通过改变图形中所有点的坐标来实现。

设原始坐标为（x，y），平移变换后的坐标为（x'，y'），则有如下公式：x' = x + dxy' = y + dy其中dx和dy分别是水平和垂直方向上的平移量。

通过改变dx和dy的值，可以实现图形的平移。

二、旋转变换（Rotation）旋转变换是将图形绕着指定点旋转一定角度的操作。

旋转变换可以通过改变图形中每个点的坐标来实现。

设原始坐标为（x，y），旋转变换后的坐标为（x'，y'），则有如下公式：x' = x*cosθ - y*sinθy' = x*sinθ + y*cosθ其中θ表示旋转的角度。

通过改变θ的值，可以实现图形的旋转。

三、缩放变换（Scaling）缩放变换是将图形按比例进行放大或缩小的操作。

缩放变换可以通过改变图形中每个点的坐标来实现。

设原始坐标为（x，y），缩放变换后的坐标为（x'，y'），则有如下公式：x' = x * sxy' = y * sy其中sx和sy分别表示在水平和垂直方向上的缩放比例。

通过改变sx和sy的值，可以实现图形的缩放。

四、错切变换（Shearing）错切变换是将图形在水平或垂直方向上斜向延伸的操作。

错切变换可以通过改变图形中每个点的坐标来实现。

设原始坐标为（x，y），错切变换后的坐标为（x'，y'），则有如下公式：x' = x + myy' = nx + y其中n和m分别表示在水平和垂直方向上的错切系数。

第四章投影变换§4.1 概述在前三章中，我们分别讨论了点、线、面及其相对位置的投影。

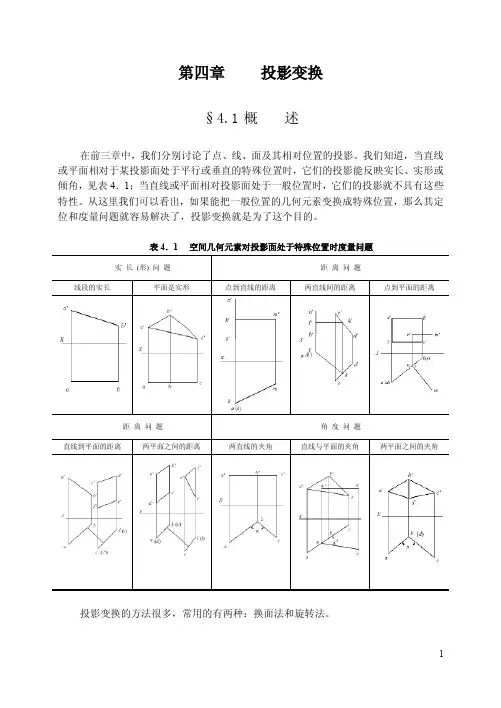
我们知道，当直线或平面相对于某投影面处于平行或垂直的特殊位置时，它们的投影能反映实长、实形或倾角，见表4．1；当直线或平面相对投影面处于一般位置时，它们的投影就不具有这些特性。

从这里我们可以看出，如果能把一般位置的几何元素变换成特殊位置，那么其定位和度量问题就容易解决了，投影变换就是为了这个目的。

表4．1 空间几何元素对投影面处于特殊位置时度量问题实长(形) 问题距离问题线段的实长平面是实形点到直线的距离两直线间的距离点到平面的距离距离问题角度问题直线到平面的距离两平面之间的距离两直线的夹角直线与平面的夹角两平面之间的夹角投影变换的方法很多，常用的有两种：换面法和旋转法。

(a) (b) (c)图4．1 点的一次换面（更换V 面）．§4.2 换面法一 换面法的基本概念换面法就是保持空间几何元素的位置不动，通过改变投影面的位置来改变空间几何元素与投影面的位置关系，从而有利于解题。

如图4．1(a)所示：点A 在V /H 体系中，正面投影为a ’,水平投影为a 。

现H 面不变，取一铅垂面V l 代替正立面V ，构成新的两投影面体系V 1/H 。

过点A 向V 1面作垂线，得到点A 在V l 面上的投影a ’1，V /H 体系为旧投影体系，X 轴为旧投影轴，而V 1/H 体系为新投影体系，X l 轴为新投影轴，V 面为旧投影面，H 面为不变投影面，V 1面为新投影面。

相应地，V 面上的投影a ’为旧投影，H 面上的投影a 为不变投影、V 1面上的投影a 1’为新投影。

在新投影体系V 1/H 中，新投影面V l 必须与旧体系V /H 中不变投影面H 垂直，才能继续保持两投影面体系中的投影规律。

当然，也可以用一个垂直于V 面的新投影面H l 替换V /H 中的H 面，从而组成如图4．2(a)所示的V /H 1体系。

图形变换技巧归纳总结图形变换是计算机图形学中常用的技术之一，通过对图像进行转换、调整，能够实现图像的旋转、缩放、翻转等效果。

本文将对图形变换的常见技巧进行归纳总结，旨在帮助读者更好地应用和理解这些技巧。

一、旋转变换旋转变换是指将图像按照一定角度进行旋转，常见的旋转变换有顺时针旋转和逆时针旋转。

在计算机图形学中，常用的旋转变换方法有仿射变换和投影变换。

1. 仿射变换仿射变换是一种线性变换，通过对图像的平移、旋转和缩放等操作，能够实现图像的旋转效果。

在仿射变换中，通过定义一个变换矩阵，可以对图像进行平移、旋转、缩放等操作。

2. 投影变换投影变换是一种非线性变换，能够实现更加复杂的图像变换效果。

投影变换通常用于实现一些特殊的效果，比如透视变换和仿射变换的组合。

通过投影变换，可以实现对图像的扭曲、转换等操作，使图像达到更加逼真的效果。

二、缩放变换缩放变换是指改变图像的比例大小，常用于图像的放大和缩小操作。

在图形学中，缩放操作通常是通过改变图像的像素点来实现的。

常见的缩放变换方法包括最近邻插值法、双线性插值法和双三次插值法。

1. 最近邻插值法最近邻插值法是一种简单的缩放变换方法，其原理是将源图像中某个像素点的值复制到目标图像中对应的位置。

这种方法操作简单，但会导致图像边缘的锯齿状现象。

2. 双线性插值法双线性插值法是一种常用的缩放变换方法，通过对源图像中像素点的插值来计算目标图像中对应位置的像素值。

这种方法可以提高图像的质量，减少锯齿状现象。

3. 双三次插值法双三次插值法是一种更加精确的缩放变换方法，它通过对源图像中一定范围内的像素点进行插值，计算目标图像中对应位置的像素值。

这种方法可以提高图像的质量，减少锯齿状现象，并且能够更好地保持图像的细节信息。

三、翻转变换翻转变换是指将图像按照水平或垂直方向进行翻转，常见的翻转变换有水平翻转和垂直翻转。

在计算机图形学中，翻转变换通常是通过对图像的像素点进行重新排列来实现的。

投影变换基本要求掌握换面法的基本原理.换面法作图的投影变换规律对投影面的倾角M量问题形的实形、§6-1概述投影变换就是将直线或平面从一般位置变换为投影 面平行或垂直的位置，以简便地解决它们的度量和 定楼间题。

当直线或平面相对于投影面处于特殊位置时，它们 的投影反映线段的实长.平面的实形及其与投影面 的倾角。

当直线或平面相对于投影面处于一般位置时，它们 的投影不具备上述特性。

HI 1:11=1 1:1 HI 珂点之间距离换面法一、换面法的基本概念二、新投彩面的选择原则三、点的投影变换规律四、四个基本问题五、旋转法简介用新的投影换面法一空间几何元素的位置保持不动，面来代替旧的投影面，使对新投影面的相对位置变成有利解题的位置，然后找出其在新投形面上的投影.二、新投影面的选择原则新投形面的选择必须符合以下两个基本条件：1.新投影面必须和空间几何元素处于有利解题的位置.2.新投影面必须垂直于一个不变投影面.三、点的投影变换规律1.点的一次变换2.点的投影变换规律3.点的两次变换2.点的投影变换规律(1)点的新投影和不变投影的连线，必垂直于新投影轴(2 )点的新投影到新投影轴的距离弟于点的旧投影到旧投够轴的距离。

"-点在V7H/体系中的投影3点的两次变换（一）把一般位置直线变为投影面平行线（二）把一般位置直线变为投影面垂直线（三）把一般位置平面变为投影面垂直面（四）把一般位置平面变为投影面平行面-（一）把一般位置直线变为投影面平行线［例题1］把一般位置直线变为投影面平行线（二）把一般位置直线变为投影面垂直线把一般位置直线变为投影面垂直线1例题2］求点C到直线A3的距离作图（三）把一般位置平面变为投影面垂直面［例题4］求点S到平面的距离距离求E 点的正面投影"。

『例题5］己知E 到平面ABC 的距离为N, （四）把一般位置平面变为投影面平行面 实形五、旋转法简介旋转法是让几何元素在空间绕垂直轴线转 动，产生新的投影的方法。