下载文档原格式
第一届小学“希望杯”全国数学邀请赛四年级第1试1．下边三个图中都有一些三角形，在图A中，有______个；在图B中，有______个；在图C中，有______个。
2．写出下面等式右边空白处的数，使等式能够成立:0.6＋0.06＋0.006＋…＝2002÷______ 。
3．观察1，2，3，6，12，23，44，x，164的规律，可知x ＝______ 。
4．如图，将一个三角形(有阴影)的两条边分别延长2倍，得到一个大三角形，这个大三角形的面积是原三角形面积的______倍。
5．如果规定a※b ＝13×a－b÷8，那么17※24的最后结果是______。
6．气象局对部分旅游景区的某一天的气温预报如下表：其中，温差最小的景区是______ ，温差最大的景区是______。
7．AOB是三角形的纸，OA＝OB，图中的虚线是折痕，至少折______ 次就可以得到8个相同的三角形。
8．有的两位数，加48，就变成3位数；减48，就变成1位数，这样的两位数有______ ，它们的和等于_____ 。
9．甲、乙、丙、丁四个学习小组共有图书280本，班主任老师提议让四个组的书一样多，得到拥护，于是从甲调14本给乙，从乙调15本给丙，从丙调17本给丁，从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书______ 本。
10．幼儿园老师给几组小朋友分苹果，每组分7个，少3个；每组分6个，则多4个，苹果有______ 个，小朋友共______ 组。
11．在 a＝20032003×2002和 b＝20022003×2003中，较大的数是______ ，它比较小的数大______ 。
12．小明的家离学校2千米，小光的家离学校3千米，小明和小光的家相距______ 千米。
13．甲、乙、丙三人中只有1人会开汽车。
甲说：“我会开。
”乙说：“我不会开。
”丙说：“甲不会开。
”三人的话只有一句是真话。
2023希望杯四年级100题及解析摘要：：1.希望杯赛事介绍2.2023年希望杯四年级100题概述3.题目分类与解析4.解题策略与技巧5.实战演练与总结正文：正文：希望杯赛事介绍“希望杯”是全国青少年数学竞赛的一项重要赛事，旨在选拔优秀的学生，激发青少年学习数学的兴趣，提高数学素养。
每年都有大量的四年级学生参加这个比赛，以下是我们为您准备的2023年希望杯四年级100题及解析。
2023年希望杯四年级100题概述2023年希望杯四年级100题涵盖了算术、几何、逻辑、应用等多个方面，题目设计巧妙，富有挑战性。
这些题目不仅能够检验学生的数学基本功，还能提高学生的思维能力和解决问题的能力。
题目分类与解析我们将这些题目分为以下几个类别：1.算术类：包括基本的加减乘除，分数、小数、百分数的计算等。
2.几何类：涉及平面几何、立体几何的知识，如角度、边长、周长、面积、体积等的计算。
3.逻辑类：通过逻辑推理，找出规律，解决问题。
4.应用类：将数学知识应用到日常生活中，解决实际问题。
解题策略与技巧1.熟悉基本概念和公式：解答题目前，确保对基本概念和公式有清晰的理解。
2.善于画图：几何类题目中，画图能够帮助更好地理解问题，找到解题思路。
3.逻辑思维：逻辑类题目中，运用逻辑思维，找出规律。
4.善于转换：将复杂问题转化为简单问题，以便更容易解决。
实战演练与总结以下为2023年希望杯四年级100题的部分题目及解析，供您参考：（此处插入部分题目及解析）希望这些题目和解析对您有所帮助。
在准备希望杯比赛时，多做练习题，总结经验，相信您会在比赛中取得好成绩。
2023年希望杯四年级100题及解析下列哪个数既是2的倍数又是5的倍数？A. 3B. 5C. 8D. 10一个正方形的边长增加3厘米，它的面积增加多少平方厘米？A. 3B. 6C. 9D. 无法确定一个数除以3余2，除以5余4，除以7余6，这个数最小是多少？A. 12B. 19C. 26D. 33下列哪个式子表示的是乘法分配律？A. (a + b) ×c = a ×c + bB. a ×b ×c = a ×(b ×c)C.a ×(b + c) = a ×b + a ×cD. (a + b) + c = a + (b + c)下列哪个图形是轴对称图形？A. 等边三角形B. 平行四边形C. 梯形D. 圆形1千克苹果和2千克梨共花12元，2千克苹果和1千克梨共花14元，则1千克苹果和1千克梨共花多少元？A. 6B. 7C. 8D. 9下列哪个算式的结果等于8？A. 2 ×4B. 3 + 5C. 6 - 2D. 16 ÷2下列哪个算式的商最大？A. 24 ÷3B. 24 ÷4C. 24 ÷6D. 24 ÷8解析：【答案】D【解析】既是2的倍数又是5的倍数的数一定是10的倍数，因此选D。
【答案】D【解析】正方形的边长增加3厘米，面积增加的部分是一个长3厘米、宽为原正方形边长的新矩形。
由于原正方形的边长未知，因此无法确定增加的面积。
【答案】B【解析】根据题意，这个数除以3余2，除以5余4，除以7余6，那么这个数加1就能被3、5、7整除。
3、5、7的最小公倍数是3×5×7=105，所以这个数最小是105-1=104，但选项中并没有104，所以我们需要继续找下一个符合条件的数。
105×2-1=209，但选项中并没有209。
105×3-1=314，但选项中并没有314。
希望杯四年级试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项是正确的？A. 2+3=5B. 3+4=7C. 5+5=10D. 4+5=9答案：C2. 哪个图形是正方形？A. □B. ○C. △D. ▢答案：A3. 以下哪个单词拼写正确？A. colerB. colerfulC. colerfullD. colorful答案：D4. 下列哪个是正确的分数？A. 1/2B. 2/1C. 3/1D. 4/2答案：A5. 哪个数字是最小的？A. 3B. 2C. 1D. 0答案：D6. 下列哪个选项是正确的？A. 4-2=1B. 5-3=2C. 6-4=3D. 7-5=4答案：B7. 哪个是正确的乘法？A. 2×3=6B. 3×4=10C. 4×5=15D. 5×6=30答案：A8. 哪个是正确的除法？A. 8÷2=3B. 9÷3=2C. 10÷4=2D. 12÷6=1答案：B9. 下列哪个是正确的时间？A. 12:00 PMB. 12:00 AMC. 6:00 PMD. 6:00 AM答案：A10. 哪个是正确的月份？A. 一月B. 二月C. 三月D. 四月答案：B二、填空题（每题4分，共20分）1. 一个长方形的长是6厘米，宽是4厘米，它的面积是______平方厘米。
答案：242. 一个数的3倍是9，这个数是______。
答案：33. 一个数加上5等于10，这个数是______。
答案：54. 一个数减去2等于3，这个数是______。
答案：55. 一个数乘以2等于8，这个数是______。
答案：4三、解答题（每题5分，共20分）1. 一个苹果比一个梨重200克，如果一个苹果重500克，那么一个梨重多少克？答案：一个梨重300克。
2. 小明有10个苹果，他给了小红3个，然后又买了5个，小明现在有多少个苹果？答案：小明现在有12个苹果。
第希望杯考前训练题四年级HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】第16届希望杯考前训练100题学前知识点梳理主要针对“希望杯”全国数学邀请赛进行考前特训，主要学习内容有：1.整数的四则运算，运算定律，简便运算。
2.基本图形，图形的拼组（分、合、移、补），图形的变换，折叠与展开。
3.角的概念与度量，长方形、正方形的周长和面积，平行四边形、梯形的概念和周长计算。
4.整除概念，数的整除特征，带余数除法，平均数。
5.几何计数（数图形），找规律，归纳，统计，可能性。
6.数谜，分析推理能力，数位，十进制表示法。
7.生活数学（钟表，时间，人民币，位置与方向，长度，质量的单位）。
8.应用题（植树问题、年龄问题、鸡兔同笼、盈亏问题、行程问题）。
考前100题选讲1.计算：8×27×25。
2.计算：9+98+987+9876。
3.计算：2-4+6-8+10-12+…-48+50。
4.计算:2017×2016+2016×2014-2015×2016-2015X2017。
5.计算:15÷7+68÷14。
6.已知999999÷（a÷2)=142857，求a7.某数被27除，商是8，余数是5，求这个数。
8.定义：A*B=（A+3)×（B-2)，求15*17。
9.除法算式△÷7=12……□中，余数最大是多少？10.有5个连续偶数之和恰好等于4个连续奇数之和，如4+6+8+10+12=7+9+11+13。
请写出一个符合要求的式子。
11.将36表示成三个大于1的自然数的乘积（不考虑三个自然数的相乘顺序）。
共有几种不同的表示方法？12.用数字2，0，1，7可以组成多少个不重复的三位数？13.用2295除以一个两位数，丽丽在计算的时候错把这个两位数的十位数字和个位数字写反了，得到的结果是45，则正确的结果应该是多少？14.如果把某个除法算式的被除数152写成125，则商会比原来的结果小3，且余数不发生变化，求余数？和某个小于100的自然数的和正好等于两个连续自然数之积，求这个小于100的自然数。
全国四年级希望杯数学竞赛全部试题与答案一、竞赛介绍“希望杯”是全国小学生奥数竞赛之一，自1996年创办以来，已经成为小学生数学竞赛中最有影响力的赛事之一。
本次比赛是面向四年级的“希望杯”数学竞赛，包含两个考试科目：数学（含应用题）和口算。
这个文档将介绍全部试题和答案。
二、数学试题试题一下列哪一个数是偶数？A. 1B. 3C. 5D. 2答案D. 2试题二根据下列算式，1 + 2 + 3 + 4 + 5 + 6 = ?A. 15B. 18C. 20D. 21答案D. 21试题三张三一周的零花钱是12元，他每天都要花1元，那么他一周之后还剩下多少钱？A. 5元B. 6元C. 7元D. 8元B. 6元试题四计算：（1 + 2 - 3）× 5A. 0B. 5C. 10D. 15答案B. 5试题五根据下列数字，找到其中的三个连续数字使它们的和最大。
{3, 6, 8, 2, 7, 1, 9, 0}A. 3, 6, 8B. 8, 2, 7C. 1, 9, 0D. 6, 8, 2答案B. 8, 2, 7三、口算试题试题一计算：1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10答案55试题二计算：9 × 5答案45计算：16 ÷ 4答案4试题四计算：47 - 23答案24试题五计算：200 ÷ 8答案25四、以上是全国四年级希望杯数学竞赛的全部试题和答案。
经过这次竞赛的练习，寻找方法和答案的过程不仅能够锻炼孩子们的思维能力和逻辑思维能力，同时也是对他们平时所学知识的一种回顾和检验。
希望这份文档能够对您有所帮助。
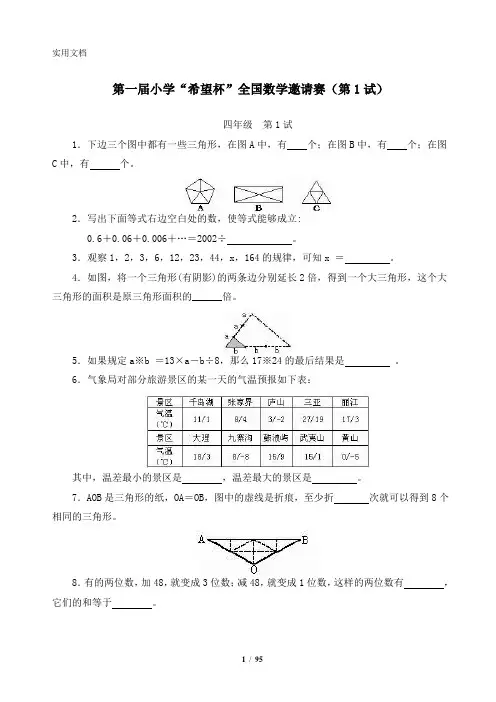
第一届小学“希望杯”全国数学邀请赛（第1试）四年级第1试1．下边三个图中都有一些三角形，在图A中，有个；在图B中，有个；在图C中，有个。
2．写出下面等式右边空白处的数，使等式能够成立:0.6＋0.06＋0.006＋…＝2002÷。
3．观察1，2，3，6，12，23，44，x，164的规律，可知x ＝。
4．如图，将一个三角形(有阴影)的两条边分别延长2倍，得到一个大三角形，这个大三角形的面积是原三角形面积的______倍。
5．如果规定a※b ＝13×a－b÷8，那么17※24的最后结果是。
6．气象局对部分旅游景区的某一天的气温预报如下表：其中，温差最小的景区是，温差最大的景区是。
7．AOB是三角形的纸，OA＝OB，图中的虚线是折痕，至少折次就可以得到8个相同的三角形。
8．有的两位数，加48，就变成3位数；减48，就变成1位数，这样的两位数有，它们的和等于。
9．甲、乙、丙、丁四个学习小组共有图书280本，班主任老师提议让四个组的书一样多，得到拥护，于是从甲调14本给乙，从乙调15本给丙，从丙调17本给丁，从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10．幼儿园老师给几组小朋友分苹果，每组分7个，少3个；每组分6个，则多4个，苹果有个，小朋友共组。
11．在 a＝20032003×2002和 b＝20022003×2003中，较大的数是，它比较小的数大。
12．小明的家离学校2千米，小光的家离学校3千米，小明和小光的家相距千米。
13．甲、乙、丙三人中只有1人会开汽车。
甲说：“我会开。
”乙说：“我不会开。
”丙说：“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14．为了支援西部，1班班长小明和2班班长小光带了同样多的钱买了同一种书44本，钱全部用完，小明要了26本书，小光要了18本书。
回校后，小明补给小光28元。
小明、小光各带了元，每本书价元。
小学四年级希望杯数学练习题在小学四年级的学习过程中，数学是一个重要的学科。
希望杯数学练习题是一个很好的资源，可以帮助学生加深对数学概念的理解和掌握。
接下来，我们将介绍一些小学四年级希望杯数学练习题。
第一部分：加法和减法1. 小明有5个苹果，他又买了3个苹果，那么他一共有多少个苹果？2. 玛丽有9个橙子，她给了小红2个橙子，那么她还剩下多少个橙子？3. 有7个小鸟在树上，其中有2只飞走了，剩下多少只鸟在树上？4. 有10个糖果，小明吃掉了4个，那么还剩下几个糖果？5. 有6个小猫在院子里玩耍，其中有3只回家了，还有几只小猫在院子里？第二部分：乘法和除法1. 小明有3个口袋，每个口袋里有4个苹果，那么他一共有多少个苹果？2. 爸爸有12个饼干，他想分给每个孩子3个饼干，可以分给几个孩子？3. 有15本书，把它们放到3个书架上，每个书架上放几本书？4. 有8个小朋友，他们准备分享24个糖果，每个人可以得到几个糖果？5. 有16个蜜蜂，把它们平均分成4组，每组有几只蜜蜂？第三部分：多步运算1. 小明去超市购买饮料，每瓶饮料售价为5元，他买了3瓶饮料，给了售货员10元，请问他找回多少钱？2. 小红有10颗苹果，她打算把它们放到两个篮子里，每个篮子放的苹果数量相同，请问每个篮子里应该放几颗苹果？3. 有15个学生在教室中，他们坐在3排座位上，每排座位上有几个学生？4. 有一瓶果汁，容量为500毫升，小明喝了200毫升，小红喝了150毫升，还剩下多少毫升果汁？5. 一本书有48页，小明每天读6页，他需要多少天才能读完这本书？通过以上习题的练习，小学四年级的学生可以更好地巩固和应用他们在加法、减法、乘法和除法方面的知识。
希望杯数学练习题为学生提供了一个在课堂外进行数学练习和巩固的机会，帮助他们更好地理解和掌握数学知识。
总结：希望杯数学练习题是小学四年级学生学习数学的利器，通过这些练习题，学生可以加深对加法、减法、乘法和除法的理解和掌握。
2024 IHC 4培训题1. 1+3+5+7+……+47+49=________。
2. 计算：9＋98＋987+9876=________。
3. 计算：( 1 + 2 + 3 + … + 29 + 30 ) × 6 – 6 × 128 =________。
4. 计算：(123202220232022321)2023++++++++++÷=……_______。
5. 下面算式中数字1~9各出现一次，其中3，5，7，9已经填好，那么这个算式的计算结果是________。
6. 从1，2，3，4，5，6六个数中选出5个填入下面式子，则算式结果最大是________。
7. 把1、2、3、4、5、6、7、8填入下面算式中，使得数最大。
这个最大得数是________。
8. 巧添符号：66 6 6 = 4。
（可以加括号）9. 在下面的式子里添上括号，使等式成立。
7 × 9 + 12 ÷ 3 – 2 = 2310. 将35分拆成若干个连续自然数的和，一共有________种不同的方法。
11.下面算式中，相同的字母代表相同的数字，不同的字母代表不同的数字。
那么A+B+C+D=________。
12.在方框中填入适当的数字，使乘法竖式成立，计算结果是________。
13.如果一个四位数与一个三位数的和是1999，并且四位数和三位数是由7个不同的数字组成的。
那么，这样的四位数最多有_________个。
14.定义新运算：a☉b = a × (b – 21) ÷ 20。
那么2021☉2021 =________。
15.解方程：21.21x + 5289 ÷ (111 × 9 – 876) × 47 = 4321 + 1.21x，则x =________。
16.有一个以数字6开头的1001位数，它的任意相邻两位数都是17或23的倍数，那么这个数的最末六位数是________。
第16届希望杯考前训练100题学前知识点梳理主要针对“希望杯”全国数学邀请赛进行考前特训，主要学习内容有：1.整数的四则运算，运算定律，简便运算。
2.基本图形，图形的拼组（分、合、移、补），图形的变换，折叠与展开。
3.角的概念与度量，长方形、正方形的周长和面积，平行四边形、梯形的概念和周长计算。
4.整除概念，数的整除特征，带余数除法，平均数。
5.几何计数（数图形），找规律，归纳，统计，可能性。
6.数谜，分析推理能力，数位，十进制表示法。
7.生活数学（钟表，时间，人民币，位置与方向，长度，质量的单位）。
8.应用题（植树问题、年龄问题、鸡兔同笼、盈亏问题、行程问题）。
考前100题选讲1.计算：8×27×25。
2.计算：9+98+987+9876。
3.计算：2-4+6-8+10-12+…-48+50。
4.计算:2017×2016+2016×2014-2015×2016-2015X2017。
5.计算:15÷7+68÷14。
6.已知999999÷（a÷2)=142857，求a7.某数被27除，商是8，余数是5，求这个数。
8.定义：A*B=（A+3)×（B-2)，求15*17。
9.除法算式△÷7=12……□中，余数最大是多少？10.有5个连续偶数之和恰好等于4个连续奇数之和，如4+6+8+10+12=7+9+11+13。
请写出一个符合要求的式子。
11.将36表示成三个大于1的自然数的乘积（不考虑三个自然数的相乘顺序）。
共有几种不同的表示方法？12.用数字2，0，1，7可以组成多少个不重复的三位数？13.用2295除以一个两位数，丽丽在计算的时候错把这个两位数的十位数字和个位数字写反了，得到的结果是45，则正确的结果应该是多少？14.如果把某个除法算式的被除数152写成125，则商会比原来的结果小3，且余数不发生变化，求余数？15.2017和某个小于100的自然数的和正好等于两个连续自然数之积，求这个小于100的自然数。
16.某两位数的十位数字与个位数字互换后，新数比原数大36，求原来的两位数。
17.abc是一个三位偶数，已知b是c的三倍，且b=a+c，求abc。
18.在乘法运算15×16×17×18×19×20×21×22×23×24×25的计算结果中，最后有多少个连续的0？19.在2018后面加一个两位数，使它成为一个能被7整除的六位数，则这个两位数最大的是多少？20.求能同时被3，5，7整除的最小的五位数。
21.用一个自然数分别去除25，38，43，三个余数之和为18，求这个自然数。
22.一个数被3除余2，被5除余4，被7除余6，则这个数最小是几？23.自然数a是3的倍数，a-2是4的倍数，a-3是5的倍数，则a最小是多少？24.a，b，d是一位数字，并且ab-cd=21，cd1-1ab=6，则ad等于多少。
25.求能被2，3，5整除的最小四位数。
26.488□是一个四位数，数学老师说:“我在这个口中先后填人3个数字，所得的3个四位数，依次可被9，11，7整除。
”数学老师先后填人的3个数字和是多少？27.从1，2，3，4，5，6这6个数字中，任取2个组成两位数，这些两位数中，3的倍数有多少个？28.已知x，y是大于0的自然数，且x+y=100。
若x是3的倍数，y是5的倍数，则（x，y）的不同取值有几对？29.如图1的算式中，A，B，C，D，E，F表示不同的一位数，求A，B，C，D，E，F表示的数。
30.在1500中，不能被2整除，也不能被3整除，又不能被5整除的数有多少个？31.在1到200之间去掉所有完全平方数，剩下的自然数的和是多少？32.如图2，共端点A的射线a与d互相垂直，a与c的夹角是60°。
b与d的夹角是45°，求b与c夹角的度数。
33.如图3，在正方形ABCD中，CM=3BM，若梯形AMCD的周长比△ABM的周长大6，求正方形的边长。
34.将同样的两张正方形透明塑料薄片部分重合地放于桌面上（如图4，S+S=正方形)，已加ABCD的周长是60厘米，求长方形ABCD的面积。
35.如图5，一只小蚂蚁从点A出发，沿折线爬行一周，问:小蚂蚁爬行了多少米？36.一个长方形的长和宽都增加3厘米后，长方形的面积增加了63平方厘米，求原长方形的周长。
37.用长是22厘米的铁丝围成一个长和宽都是整厘米数的长方形，有几种方法？38.如图6，∠1+∠2+∠3+∠4+∠5+∠6=180°，图中比平角小的角有多少个？39.如图7用11个边长为1的正方形卡片拼成数字“2”，求图中长方形的个数（不包括正方形）。
40.数一数，图中共有多少个平行四边形？41.数一数，图中有多少个三角形？42.数一数，图中有多少个三角形？43.已知一列数:1，3，4，7，11，18，…，这列数的第10个是多少？44.有白棋子和黑棋子共2018枚，按照图11的规律从左到右排成一行，其中黑棋子多少枚？45.观察下面按一定规律排列的一列数：112123123412334445555，，，，，，，，，，，……求第2017个数。
46.如图12，用小正方形摆成下列图形，按摆放规律，第25个图形需要多少个小正方形？47.如图13所示的数字是电子表中经常可见的数字2和5的表示形式，把图中左边的数字2向右翻转一次可得到右边的数字5，再向右翻转一次又会得到原来的数字2，那么将图2所示的数字25翻转一次得到的数字是多少？48.有张，王，李三个工人，甲、乙、丙三个工厂，以及车工，钳工和电工三种工作，已知：①王不在甲厂；②张不在乙厂；③在甲厂的不是钳工；④在乙厂的是车工；⑤王不是车工。
这三个人分别在哪个工厂，干什么工作？49.一个两位数除以它的各位数字之和，余数最大是多少？50.5个人围成一圈做游戏，每人都有一袋小石子。
游戏开始时，第一个人给第二个人1颗石子，第二个人给第三个人2颗石子，第三个人给第四个人3颗石子，第四个人给第五个人4颗石子，第五个人给第一个人5颗石子，……，如此操作5圈后所有人袋中的石千都一样多。
若所有石子的总数为1990颗，问游戏前每个人袋中分别有多少颗石子？51.将2017个小球放到10个箱子中，要求每个箱子中的小球的数目中都带有数字7.请给出一种摆放方法。
52.箱子里有2018个小球，编号分别为1，2，3，…，2018。
现从箱子中摸出1616个小球，将它们的编号相乘，求积的个位数字。
53.自然数n的十位数字是4，个位数字是2，各个数位上的数字之和为42，且是42的倍数，求满足上述条件的最小的自然数。
54.一副扑克牌有52张，依惯例A，J，Q，K依次视为1点，11点，12点，13点，任意抽出若干张牌，不计花色，如果抽出的牌中必定有3张牌的点数相同，那么至少要取几张牌？如果抽出的牌中必定有2张牌的点数之和等于15，那么至少要取几张牌？55.小明、小强、小红三个人在一起玩捉速藏的游戏，小明对小强说:“我在你的正北方5米处”，小红对小强说:“我在你的正南方6米处”。
若小强走1米需要6步，那么先抓小明再去抓小红一共需要走多少步？56.10个50g的砝码和5个100g的砝码同时放在天平的左右两侧才能使天平保待平衡，那么在天平左侧放2个1kg的砝码，右侧放6个300g的砝码，要使天平保持平衡还要在右侧放几个50g的砝码。
57.在一个周长是200米的池塘周围植树，每隔5米植一棵，需要准备多少棵树苗？58.在120米长的跑道右侧插16面彩旗，求相邻两面彩旗之间的距离。
59.今年，小军4岁，爸爸31岁，再过多少年爸爸的年龄是小军的4倍。
60.亮亮比晶晶小6岁，16年后亮亮的年龄是晶晶今年的年龄的2倍，问:晶晶今年几岁？61.父亲今年45岁，儿子今年15岁，多少年前父亲的年龄是儿子年龄的7倍？62.2011年，妈妈的年龄等于她的两个孩子的年龄和的5倍，2017年她的年龄等于两个孩子的年龄和的2倍。
求2018年时妈妈的年龄。
63.某学习小组数学成绩的统计图如图14，求该小组的平均成绩。
64.统计十位同学在一次数学考试中的成绩，已知前四名的平均分是93分，后六名的平均分比十人的总平均分少6分，求这十位同学的平均分。
65.李家承包了100亩地种玉米，亩产量600斤，刘家比李家少承包了20亩，结果两家的总产量相同，问：（1)刘家玉米的总产量是多少斤？（2)李家玉米的亩产量比刘家的少多少斤？66.橘子、苹果、梨共有六箱，这六箱水果的重量（单位：千克)分别为:15，16，18，19，20，31，其中苹果的重量是梨的一半，橘子只有一箱。
这六个箱子中分别装的是什么水果？67.每本书的版权贞上都印有:开本、印张，字数，定价等等。
如:“开本:720mm*960mm 1/16 印张:12 字数:240千字”。
求这本书平均每页有多少字？（注:16开，即1个印张16页)68.某校规定语文，英语，数学三料考试成绩的平均分在95分以上才有可能被评为三好学生，若在一次期末考试中，希希语文考了96分，英语考了92分，那么他数学至少得多少分才有可能被评为三好学生？69.1个西瓜可换5个苹果，2个苹果可换3根香蕉，5根香蕉可换8个桃子，那么60个桃子可换几个西瓜？70.7头牛可换16只羊，2只羊可换21只兔，则3头牛可换多少只兔？71.有两块地，平均亩产粮食650千克，其中第一块地5亩，亩产粮食670千克。
如果第二块地亩产粮食645千克，第二块地有多少亩？72.妈妈去市场买菜，已知买肉和鸡蛋共用了77元，买鸡蛋和青架共用了60元，买肉和青菜共用了103元，那么，买青菜用了多少钱？73.已知5个连续奇数的和是125，求其中最小的奇数。
74.2018是4个连续自然数的和，其中最大的数是多少。
75.两个数的和是900，其中较大数是较小数的19倍，则这两个数分别是多少？76.甲、乙，丙三数之和为180，乙比丙的3倍少2，甲比丙的2倍多8，求甲、乙、丙三数。
77.8个连续的自然数从小到大排列，若后5个数的和比前3个数的和的2倍大12，求这8个数中最小的数。
78.甲、乙两校共有学生432人，为了照顾学生就近人学，经协商由甲校调入乙校16人，这样甲校比乙校还多24人。
问甲、乙两校原来各有多少人？79.学校里有排球24个，足球的个数比排球的2倍少5个，学校有排球、足球共多少个？80.某商店从皮具厂以每个100元的价格购进了60个皮箱，这些皮箱共卖了8100元。
这个商店从这60个皮箱上共获得多少利润？每个皮箱盈利多少元？81.买5斤西红柿用了12元，比买6斤茄子少用了1元8角。
