当前位置：文档之家 › 附录 截面的几何性质(材料力学)PPT课件

附录 截面的几何性质(材料力学)PPT课件

  • 格式：ppt
  • 大小：1003.00 KB
  • 文档页数：30

下载文档原格式

  / 30

合集下载

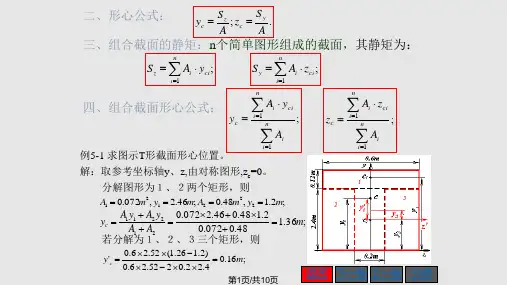
附录Ⅰ常见截面的几何性质PPT课件

附录Ⅰ常见截面的几何性质PPT课件

IP
2dA;
A
简单图形的极惯性矩可由定义式积分计算。
实心圆截面：
IP
D 2
2
2dA
D4
;
0
32
空心圆截面：
IP
D4
32
(1 4 );(
d) D
二、惯性矩(转动惯量）：
定义：平面图形中任一微面积dA对z轴、y轴的惯性矩分别为： y2dA和Z2dA；则整个图形（面积为A)对z轴、y轴的惯性矩分别为：
I
Iz
z A
bh3 12
y 2 dA; ; Iy
Iy h b3
; 12
z 2 dA;
A
圆形截面：I y
Iz
D4
64
;
几何关系：
IP
2dA
A
(y2
A
z2 )dA
IZ
Iy.
四、惯性积：
I zy
z y dA;
A
五、平行移轴公式：
I z1 z a2 A; y1 y b2 A;
第9页/共10页
返回 下一张 上一张 小结
感谢您的观看！
第10页/共10页
;
Ai
i 1
解：取参考坐标轴y、z,由对称图形,zc=0。 分解图形为１、２两个矩形，则
A1 0.072m2, y1 2.46m; A2 0.48m2, y2 1.2m;
y若c 分A解1Ay1为1 １AA22、y2 ２ 、0.0３72三0.02个.742矩6形00.4.，488则1.2 1.36m;
返回 下一张 上一张 小结
小结
一、静矩： Sz A y dA A yc ;
Sy
z
A
dA

《材料力学》课程讲解课件附录I平面图形几何性质

《材料力学》课程讲解课件附录I平面图形几何性质

解：
y
d
S x
yd A
A
2 yb( y) d y
0
b(y)
C
xc
yc
d
2 y2
R2 y2 d y d3
0
12
x
d
yc
Sx A
d3 12 πd 2 8
2d 3π
b( y) 2 R2 y2
29
yc
Sx A
d3 12 πd 2 8
2d 3π
y
2、求对形心轴 xc 的惯性矩
Ix
πd 4 64 2
3、惯性积是对轴而言。
y
z
dA
4、惯性积的取值为正值、负值、零。
y
5、规律：
o
z
20
5、规律：
Izy
zydA
A
0
y
dA z z dA
y
y
z
o
两坐标轴中，只要有一个轴为图形的对称轴，则 图形这一对坐标轴的惯性积为零。
21
对比记忆 静矩、形心；惯矩和惯性半径；它们都是反映截
面面积关于坐标轴分布情况的物理量。 静矩=（面积）（形心坐标） 惯矩=（面积）（惯性半径）2
z
o
dA y
z
全面积对z轴的惯性矩: I z y2dA,
2 z2 y2
全面积对y轴的惯性矩: I y A z2dA
A
15
Iz y2dA, I y z2dA
A
A
y
z
dA
y
o
z
2、量纲：［长度］4；单位：m4、cm4、mm4。 2 z2 y2
3、惯性矩是对轴而言（轴惯性矩）。
A

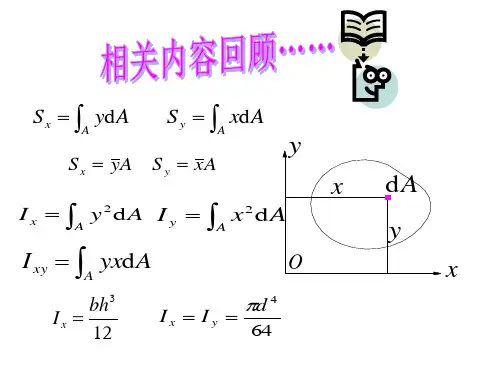
材料力学 附录_2

材料力学 附录_2
2
267 104 mm4
附录I 截面的几何性质
于是有组合截面对于两主轴x轴和y轴的惯性矩分别为
I x I x1 2 I x2 3690 10 4 mm 4 2 2110 10 4 mm 4 7910 10 4 mm 4 I y I y1 2 I y2 431 10 4 mm 4 2 267 10 4 mm 4 965 10 4 mm 4
附录I 截面的几何性质
解：将原平面图形分成上中下三个矩形。过形心建立参考坐标 系
40 53 5 603 I x 2I x1 I x2 2 40 5 27.52 12 12 y 4 4 393333 mm 39.33cm I y 2 I y1 I y2
I yC 218.415 cm 形心位置如图所示 90 mm×90 mm×12 mm 等边角钢截面
4
A 20.30 cm 2 I xC I yC 149.22 cm 4
形心位置如图所示
附录I 截面的几何性质
组合截面的形心C在对 称轴x上。以两个角钢截面的 形心连线为参考轴,只需求组 合截面形心C以该轴为基准 的横坐标 x ：
a
x
附录I 截面的几何性质
例题
图示组合截面由一个 25c号槽钢截面和两个 90 mm×90 mm×12 mm等边角钢截面组成。 试求此截面分别对于形 心轴x和y的惯性矩Ix 和 Iy 。
附录I 截面的几何性质
解: 1. 求组合截面的形心位置
由型钢规格表查得：25c号槽钢截面 A 44.91cm 2， I xC 3 690.45 cm4
I x1 y1 dA
2 A
x1 x cos y sin y1 x sin y cos

材料力学截面的几何性质课件

材料力学截面的几何性质课件
材料力学截面的几何 性质课件
目录
• 截面的基本性质 • 截面的二次矩 • 截面的抗弯截面系数 • 截面的抗扭截面系数 • 材料力学截面的应用
01 截面的基本性质
截面的面积
面积
截面面积是二维平面图形被截后，与 原图形相比增加的面积。对于矩形、 圆形、三角形等简单形状，截面面积 可以通过几何公式直接计算。
的刚度和稳定性。
截面惯性矩
截面惯性矩是衡量截面抗弯刚度 的指标，对于承受弯矩的构件， 选择具有较大惯性矩的截面可以
减少挠度和转角。
截面抵抗矩
截面抵抗矩是衡量截面抗剪切能 力的指标，对于承受剪力的构件 ，选择具有较大抵抗矩的截面可
以增加构件的承载能力。
工程设计中的应用
桥梁设计
在桥梁设计中，需要考虑梁的截面尺寸、材料类型和截面形式等 因素，以确保桥梁具有足够的强度和刚、单位等因素，以确保数 据处理结果的准确性和可靠性。
1.谢谢聆 听
根据微面积和其对应的主 轴方向余弦，计算出截面 二次矩。
主轴的确定
根据计算出的惯性矩，找 出三个主轴的方向余弦和 角度。
实例分析
圆截面
圆截面的二次矩为常数， 且各主轴与截面垂直，说 明圆截面在弯曲时没有翘 曲的趋势。
矩形截面
矩形截面的二次矩与宽度 的平方成正比，说明矩形 截面有较好的抗弯能力。
工字形截面
工字形截面的二次矩比同 样面积的矩形截面小，但 抗弯能力仍高于同样重量 的实心杆件。
03 截面的抗弯截面系数
定义与性质
01
抗弯截面系数是截面对其轴线的惯性矩除以截面的面积 得到的数值，用来度量截面在弯矩作用下抵抗变形的能 力。
02
不同形状的截面有不同的抗弯截面系数，如圆截面为1 ，矩形截面为1.13，工字形截面为1.44等。

材料力学截面的几何性质课件

材料力学截面的几何性质课件

截面的对称性
截面可以是对称的或非对称的。
对称截面是指沿中心线对称的截面，如圆形、正 方形等。
非对称截面是指不沿中心线对称的截面，如椭圆 形、三角形等。
截面的重心
重心是物体质量的集中点，对于规则形状的物体，重心位置可以通过几何计算得 到。
对于截面，重心是截面质量的集中点，其位置可以通过计算截面的面积和质量得 到。
材料力学的发展历程
总结词
材料力学的发展经历了多个阶段，从最早的实验观察到现代的理论建模和计算机模拟。
详细描述
最初的材料力学研究主要基于实验观察和经验总结，随着数学和物理学的发展，人们开始建立更精确 的理论模型，并使用计算机进行模拟和分析。这些理论模型和方法在解决复杂工程问题方面发挥了重 要作用。
02
意义
主惯性矩是衡量截面抗弯和抗扭能力的一个重要参数，其 值越大，抗弯和抗扭能力越强。
04
材料力学截面的弯曲性质
弯曲的定义
弯曲是指物体在力的作用下发 生形变，其中物体的一部分相 对于另一部分发生转动。
弯曲变形通常发生在梁、柱等 细长结构中，其中截面上的应 力分布不均匀。
弯曲变形可以通过施加外力或 重力等作用力引起，也可以由 热膨胀、收缩等因素引起。
扭转的变形能
1 2
变形能
物体在受到外力作用时，由于发生变形而储存的 能量称为变形能。
扭转变形能
物体在扭转变形时，由于变形而储存的能量称为 扭转变形能。
3
扭转变形能的计算
扭转变形能可以通过计算截面上的剪切应变和剪 切胡克常数来计算。
扭转的稳定性
01
稳定性
在材料力学中，稳定性是指物体在外力作用下保持其平衡状态的能力。
剪切变形能

材料力学--附录A截面的几何性质

材料力学--附录A截面的几何性质

y
A
其中： 为截面面积 为截面面积， 、 其中：A为截面面积，x、 y轴为形心轴， x1、 y1为 轴为形心轴， 轴为形心轴 分别与x、 轴平行的轴 轴平行的轴， 分别与 、y轴平行的轴， a、b分别为相应平行轴之 、 分别为相应平行轴之 间的距离。 间的距离。
O a O1 b
z
附录A 附录
截面的几何性质
附录A 附录
截面的几何性质
静矩、 g 静矩、形心及其相互关系 惯性矩、极惯性矩、惯性积、 g 惯性矩、极惯性矩、惯性积、惯性半径 g 惯性矩与惯性积的平行移轴定理 g 惯性矩与惯性积的转轴定理 主轴与形心主轴、 g 主轴与形心主轴、主惯性矩与形心主惯性矩 组合图形形心、 g 组合图形形心、形心主轴和形心主矩的计算
试确定等腰梯形面积的形心和对底边的静矩。 试确定等腰梯形面积的形心和对底边的静矩。
y
【解】 截面对底边的静矩
Sz = A y1 + A y2 1 2
b C1
h
1 2 1 h = bh⋅ h + ah⋅ 2 3 2 3
C C2
=
h (a+2b) 6
2
O a
z
形心位置
zC = 0
Sz h a +2b yC = = ⋅ A 3 a +b
120
C1（0,0） 负面积 C2（5,5） C2 C1 C
10 80
z
yC = −20.3mm
形心C坐标为（ 形心 坐标为（-20.3， -20.3）。 坐标为 ， ）。
这两种方法所得到的形心坐标不同 是由于选择不同的坐标系引起的。 是由于选择不同的坐标系引起的。
附录A 附录 【例2】 】
截面的几何性质

材料力学课件之截面几何性质

材料力学课件之截面几何性质

d
2 2
16 43 416 (5.53 2)2 12
4123 412 (10.57 6)2 12
2416.76mm4
y
C2 C
z
C1
646 （单位mm）
y1
y2
29
Ai yi Ai Ai zi Ai
Ai yi
A
Ai zi
A
o Z1
z
Z2
使用上述公式时，对于挖掉部分的面积应取负值。
6
例2 求图示矩形截面abcd 部分对z 轴的静矩。
y
C3
C1
C2
o 2
4
6
12
123
Ai 144 72 -16
yi 6 4 6
z
zi 6 16 4
（单位：cm）
解：
yC
404
402
(mm)
402 )
12
64
4
23034100.7mm4
17
截面图形的的几何性质------形心和惯性矩
1，简单截面
1、有对称轴的截面，记忆或直接判断 教材353页附录Ⅱ
2、型钢，查表。教材356页附录Ⅲ
2，组合截面，组合法。
§Ⅰ.5惯性矩和惯性积的转轴公式,主惯性轴
一：已知 Iy、Iz、Iyz、(逆时针为正)，求 Iy1、Iz1、Iy1z1
cos 2
0
C
z
方形截面
Iz'
Iz
Iy 2
Iz
Iy 2
cos 2
I yz sin 2
Iz
Iy 2
Iz
I
y'
Iz
2
其中：
I

附录1截面几何性质精品PPT课件

附录1截面几何性质精品PPT课件

解：
dA = b dy
Ix
A y2dA
h
2h
by2dy
2
bh3 12
Iy
hb3 12
Ix A y2dA
y
dy
h
y
C
Hale Waihona Puke x2021/2/3
b
15
例 2 - 2 求圆形截面对其对称轴的惯性矩 。
解：因为截面对其圆心 O 的
极惯性矩为 y
I p
A
2dA
2 0
d /2
d 3d
0
d4
32
Ix Iy Iρ
轴平 行的坐 标轴（形心轴）
2021/2/3
yc
C(a,b)
xc
b
x
17
Ix , Iy , Ixy _____ 截面对 x , y 轴的惯性矩和惯性积。
Ixc ,Iyc , Ixc yc —— 截面对形心轴 xc , yc 的惯性矩和惯性积。
则平行移轴公式为
y
yc
I x I xc a2 A
Iy Iyc b2 A
Z1 80 Z2 0
所以截面的形心坐标为
ZC
A1 Z1 A1
A2 Z2 A2
46.7mm
2021/2/3
20 140
zc
20
1
yc yc1
ZC
2
y (yc2)
100
21
I1yC
1 12
20
1403
20
140
(80 46.7 )2
I
2 yC
1 12
100
203
100
20
(46.7)2

材料力学课件4第四章弯曲内力4-3(附录I)

材料力学课件4第四章弯曲内力4-3(附录I)

h
O
x
b
dA=b· dy
y dy y
O
h
x
b
bh I x = y dA= y bdy A h / 2 12
2 h/2 2
3
( 公式熟练掌握：宽×高3/12） 同理：
hb I y = x dA= x hdy A b / 2 12
2 b/2 2
3
例I-4：计算如图的惯性矩Ix , Iy,。 y d
将有关尺寸(mm)标在图中 y' C2
250
C1
O'
x
98 .3 26 .7
C3
26 .7
19 .21
y 0
A 24.1mm A x 4491(19.21 26.7) 2 2030 0 x
i i
.
4491 2 2030
将有关尺寸标在图中，标形心轴x-y轴 y y' 24 .1
Sx A
组合图形计算形心坐标的公式(I—2a)为：
x
A
xdA A

Sy A
S A
y ,i
Ax A
i i
y
A
ydA A
Sx Sx ,i A i yi A A A
(I—4)
形心坐标的公式(I—2a) 可改写为：
Sy Ax
常用，掌握
Sx Ay
(2) 由
Sx Ay
Sy Ax
2
y
bh h bh Sx Ay 2 3 6
h
C
b
h/3 x
补例：计算如图(a)的静矩Sz ,Sy, 图(b) Sz 。

材料力学附录I-1

材料力学附录I-1

I.2 极惯性矩 惯性矩 惯性积 2. 惯性矩
x 2 d A A I x y 2 d A A Iy

称为整个截面对y轴或x轴的惯性矩，亦称面积对轴 的二次矩，常用单位为m4或mm4。
图 I-5
I p 2 d A x2 d A y 2 d A I y I x
A A A
上式表明平面图形对任意两个互相垂直的轴的惯性矩之和等于该图 形面积对两轴交点的极惯性矩。 平面图形对过同一原点的任意两个互相垂直的轴的惯性矩之和是一个常量。
3. 惯性积
I xy
xy d A
A
称为整个截面图形A对x、y轴的惯性积。惯性积是对一对正交轴定义的，
因此也是面积的二次矩，可正、可负也可能为零，常用单位为m4或mm4。 若x、y轴中有一个轴为截面的对称轴，则整个截面对两轴的惯性积恒 等于零。可以证明，在对称轴两侧对称位置处的微面积对于两轴的惯性积 数值相等而符号相反，因此整个截面对两轴的惯性积必然等于零。若x、y 轴都为对称轴，则整个截面对两轴的惯性积自然为零。
S x S x I S xII
图 I-4 例题I-3图
由 S x I S xII 0 ，可得
S x I S xII
I.2 极惯性矩 惯性矩 惯性积 1. 极惯性矩
I p 2 dA
A
定义为整个截面对O点的极惯性矩。 极惯性矩的数值恒为正，常用单位为m4或mm4。
图 I-5
S x y d A y d A1 y d A2 A A1 A2 S y x d A x d A1 x d A2 A A1 A2
或
S x yC A yC1 A1 yC 2 A2 yCi Ai i 1 n S y xC A xC1 A1 xC 2 A2 xCi Ai i 1

材料力学课件(路桥)第5章截面图形的几何性质-PPT精选文档

材料力学课件(路桥)第5章截面图形的几何性质-PPT精选文档

A
形心轴的惯性矩。 圆
π d Ip I I 2 I y z y c c c 3 2
2
π d4 Iyc Izc 2 6 4
Ip
4 4 4 d π d π d 5 π d I I A B y A c 2 6 4 1 6 6 4
§5-4 惯性矩和惯性积的转轴定理*
截面图形的几何性质
§5–1 静矩和形心
§5–2 惯性矩、极惯性矩、惯性积
§5–3 惯性矩和惯性积的平行移轴定理 §5–4 惯性矩和惯性积的转轴定理* 截面的主惯性轴和主惯性矩
§5-1 静矩和形心 一、静矩：(与力矩类似)是面积与它到轴的距离之积。 z
Sz
y dA z y

ydA
A
S
y


zdA
§5-2 惯性矩、惯性积、极惯性矩 一、惯性矩：（与转动惯量类似） 是面积与它到轴的距离的平方之积。
Iy Iz
z
A
2
dA
z y

y 2d A

ቤተ መጻሕፍቲ ባይዱ
A
dA z y
二、极惯性矩： 是面积对极点的二次矩。
2 Ip d A Iy Iz A
三、惯性积：面积与其到两轴距离之积。
I yz yzd A
A
二、形心： (等厚均质板的质心与形心重合。)
y
质心：

m
ydm m
等厚 均质

A
yt dA t A zt dA t A


A
ydA A zdA A
Sz A Sy A
z
z
m
zdm m

材料力学课件 4附录

材料力学课件 4附录
2
I xy I x y abA
平行移轴定理
y’ y
α
x’ x
结论 :
1 2 ( I y I x ) cos 2 I xy sin 2
I y
1 2
(I y I x )
I x
1 2
(I y I x )
1 2
1 2
( I y I x ) cos 2 I xy sin 2
x
i
ci
Ai
组合图形的面积 组合图形的形心公 式为
A
A
i i
i
xc
x
i
ci
AiALeabharlann iiyc yci A i
A
i
i
二、几何图形的二次矩
惯性矩 ( moment of inertia )
y
x
Ix
dA y

A
y dA
2
Iy

A
x dA
2
r
惯性积 ( product of inertia )
不为零
习
题
A-1 A-3 A-5 A-7 A-8 (a)(c.) A-9
本章内容结束
形心 ( center of an area ) 公式
xc 1
x
x dA A
A
Sy A
yc
1
y dA A
A
Sx A
S x yc A
S y xc A
重要结论 坐标轴通过形心，则相应的静矩为零。
组合图形(combined area) 组合图形的面积矩
Sy
S
i
yi

材料力学-截面几何特性

材料力学-截面几何特性
IxC1 (70mm)3 10mm/12 28.58104 mm4 I yC1 70mm(10mm)3 /12 0.58104 mm4
I 0 xC 2 yC 2
IxC IxC1 A1 yc21 IxC2 A2 yc22 1104 mm4 1200mm2 (15mm)2 28.58mm4 700mm2 (25mm)2 100.33mm4
64
9 /2
Ix2 Ix2C A2 (a xc2 )2 28mm 4 (80mm )2 (100 17)2 8 3467mm4
组合截面对x轴的惯性矩为
I x I x1 2I x2 5333mm4 23467mm4 12270mm4
§I-4 惯性矩和惯性积的转轴公式 ·截面 的主惯性轴和主惯性矩
A
A ( yC b)2 dA
A ( yC2 2byC b2 )dA
I xC 2bSxC b2 A
Ix IxC 2bSxC b2 A
因为C为形心
SxC AyC 0
y
yC
x
dA
a
r
bC y
xC
x
I x I xC b2 A 同理：
I y I yC a2 A I xy I xC yC abA I p I pC (a2 b2 ) A
C1
80
x
图(b)
x
xi
Ai
x 1
A1x
2
A2
A
A1A2
409600 45 7700 19.7mm 9600 7700
y
yi Ai
y 1
A1
y
2
A2
A
A1 A2
609600 65 7700 39.7mm 9600 7700

材料力学-截面的几何性质

材料力学-截面的几何性质

1 2
(
I
y
Iz)
1 2
(
I
y
Iz )cos 2
I yz sin
2
I z1
1 2
(
I
y
Iz)
1 2
(
I
y
Iz )cos 2
I yz sin
2
(a)
I y1z1
1 2
(
I
y
Iz )sin
2
I yz sin
2
4.2 主惯性轴和主惯性矩(principal moment of inertia)
A
y2dA
A
z2dA
A
Iz Iy
此式说明了极惯性矩与轴惯性矩之间的关系。
z y
o
A dA
z y
惯性积
定义
I yz
yzdA
A
z A
y
dA
为图形对y、z轴的惯性积 。
z
o
y
惯性积的数值可正，可负，也可为零。惯性积的量纲是[长 度]4 ，常用单位为m4和mm4。
定理：若有一个轴是图形的对称轴，则图形对这对轴 的惯性积必然为零。
例题 试求图示图形对形心轴的惯性矩和 惯性积。
解：将图形看作是两个矩形的结合。 形心坐标为
yc 0
zc
A1z1 A1
A2 z2 A2
103.3mm
z 100
20
I CI
C
140
CII
103.3
II
a1 a2 y
y
20
求图形对y、z轴的惯性矩
z 100
I z I zI I zII
201003 140 203
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1 2 Ip
d4 64
y
d
x
材料力学Ⅰ电子教案
常见截面的惯性矩和惯性半径
z h
b
矩形
bh3 Iz 12
h iz 2 3
22
dz
Dd
z
圆形
d 4 Iz 64
d iz 4
圆环
Iz
64
(D4
d4)
D2 d2
iz
4
材料力学Ⅰ电子教案
§Ⅰ.3 惯性积
y
Ixy
xydA
A
ZZ
dA dA y
拉压变形： 扭转变形：
F l Fl
A
EA
T
IP
maxW TP
Tl
GIP
弯曲变形：
My
Iz
max
M Wz
A, IP, WP, Iz, Wz——表征截面几何性质的量
3
材料力学Ⅰ电子教案
Ⅰ-1 静距和形心
一、静矩（或一次矩） z
对单位厚度的均质薄
板，其形心坐标为：
y
xAxdA, yAydA
A
A
A
18
材料力学Ⅰ电子教案
例Ⅰ-3 计算矩形截面对其对称轴y轴和z轴的惯性矩。
解：先计算截面对z轴的惯性矩。取 平行于z轴的狭长条为微面积，即:
dAbdy
Iz
y2dAh/2by2dybh3
A
h/2
12
h
y z dz
dy
y
C
z
同理，计算对y轴的惯性矩。取
平行于z轴的狭长条为微面积，即:
b
dAhdz
Iy Iz
Iy Iz
y
即：对O点极惯矩等于对过O点同一平面内任意一对 相互垂直轴的惯矩之和。
材料力学Ⅰ电子教案
所以 I P 只与原点O有关，即
Iy Iz const
Iz 0,Iy 0 Ip恒0
材料力学Ⅰ电子教案
三、惯性半径
Ix
A
i
2 x
Iy
A
i
2 y
ix
Ix A
iy
Iy A
ix 和iy分别称为截面图形对于x轴和 y轴的惯性半径， 单位为m。
x
I p A 2 d A A x 2 y 2 d A A x 2 d A A y 2 d A I y I x
即截面图形对任意一对正交坐标轴的惯性矩之和，等 于它对该两轴交点的极惯性矩。
15
材料力学Ⅰ电子教案
z
y
dA
y' A
z'
z
o
且
2 z2y2
IP
2dA
A
(z2y2)dA A
一、惯性矩
y
定义：面积与它到轴的距离的
平方之积
x
dA
I x
A
y
2d
A
I y A x 2 d A
y x
分别称为截面图形对于z轴和y 轴的惯性矩。
惯性矩的数值恒为正，常用单位为m4 。
14
材料力学Ⅰ电子教案
二、极惯性矩
y
Ip
2dA
A
x 称为截面图形对O点的极惯性矩。
dA
2 x2 y2
y
x
80
材料力学Ⅰ电子教案
所以
x A1x1 A2x2 A1 A2
37500 20 m m 1900
y A1 y1 A2 y2 A1 A2
75500 40 m m 1900
y 10
1 x1
C(y, x)
y1
2 y2
10
o x2
x
80
材料力学Ⅰ电子教案
思考： 求下图所示截面的形心位置
定义： S x ydA
A
Sy xdA
o
A
分别称为截面图形对于z轴和y 轴的静矩。
dA z y
静矩的数值可能为正，可能为负，也可能为零，单位为m3。
4
材料力学Ⅰ电子教案
二、形心（平面图形面积的几何中心称为形心。）
z
zdA
A
Sy
AA
y
ydA A
Sz
AA
求静矩的另一公式：
z y A
o
dA z y
SzAydAAydA1AydA2AydAn
1
1
y1A1y2A2ynAn yi Ai
n
Ai zi z i1n
Ai
i1
n
Ai yi y i1 n
Ai
i1
7
材料力学Ⅰ电子教案
例 试计算图示三角形截面对于与其底边重合的x轴的静矩。 y
解： 取平行于x轴的狭长条，
dy
b(y)b(hy)
h
b(y )
h
y
dA b(hy)dy h
O
b
x
所以对x 轴的静矩为
SxAydA0 hb h(hy)ydyb62h
材料力学Ⅰ电子教案
例 试确定图示截面心 C 的位置。
解：将截面分为 1，2 两个矩形。
y 10
取 x 轴和 y 轴分别与截面 的底边和左边缘重合
n
x
Ai xi
i1 n
Ai
A1x1 A1
A2x2 A2
材料力学Ⅰ电子教案
材料力学
附录Ⅰ 截面的几何性质
2020年12月3日
材料力学Ⅰ电子教案
附录Ⅰ 截面的几何性质 §Ⅰ-1 静距和形心 §Ⅰ-2 惯性矩和惯性半径 §Ⅰ-3 惯性积 §Ⅰ-4 平行移轴公式 §Ⅰ-5 转轴公式和主惯性轴
2
材料力学Ⅰ电子教案
受力杆件的应力与应变，不仅与外力相关，而且与 截面的几何性质也相关。
Sy xA
Sx y A
5
材料力学Ⅰ电子教案
结论：
z
静矩的值与所选的坐标有
关,可正、可负，也可为零。
C
y
A
结论 ： 截面图形对通过其形心的轴的静矩为零；
反之，若截面图形对某一轴的静矩为零，则该轴必为形心轴。
材料力学Ⅰ电子教案
三、组合图形的静矩与形心
由静矩的定义知：整个截面对某轴的静矩应等于它的 各组成部分对同一轴的静矩的代数和:
y
定义为截面图形对于z轴和y 轴
的惯性积。
o
Z
① 惯性积的数值可能为正，可能为负，也可能为零， 常用单位为m4 。
② 若y , z 两坐标轴中有一个为截面的对称轴,则截面对
y , z轴的惯性积一定等于零。
23
材料力学Ⅰ电子教案
Ⅰ-4 平行移轴公式
一、平行移轴公式
z
zC
C点为截面图形的形心，
y
dA
yC轴和zC轴为一对通过形心 的形心轴,图形对形心轴的惯性
IyAz2dA bb//22hz2dzh1b23
19
材料力学Ⅰ电子教案
y
若截面是高度为h的
平行四边形，则其对形心
轴x 的惯x
bh 3 12
b (b)
20
材料力学Ⅰ电子教案
例5 求圆形截面的惯性矩。
已知
IP
2dA
A
d4 32
则
Iy Ix Ip
而
Iy Ix
所以
Iy Ix
50 10
A1
z
60
A2
10
y
yc
yc1
A1 yc2 A1 A2
A2
12
材料力学Ⅰ电子教案
例 半径为r的半圆：求半圆的形心。 解 在距 z 轴任意高度 y 处取狭长条 作为微面积，即
dA2 r2y2dy
r
y
A
ydA A
0
y2
r2
r2
y2dy
4r
3
2
材料力学Ⅰ电子教案
§Ⅰ.2 惯性矩、极惯性矩、惯性积
i1
y A1y1A2y2 A1A2
1 x1
y1
o x2
80
y2
2 10 x
材料力学Ⅰ电子教案
矩形 1 A 1 1 0 12 102 m 0 2 m 0 y 10
x15mm
y160mm
1 x1
矩形 2 y1
A 2 1 0 7 0 7m 00 2m
x21072045mm
o
y2 5mm
2 y2
10
x2