当前位置：文档之家 › 截面的几何性质

截面的几何性质

  • 格式：doc
  • 大小：310.50 KB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

材料力学第六章 截面的几何性质惯性矩

材料力学第六章 截面的几何性质惯性矩

IP
2dA
A
(y2
A
z2 )dA
IZ
Iy.
返回 下一张 上一张 小结
第三节 惯性矩和惯性积的 y1dA (y a)2 dA A
y2dA 2a ydA a2 dA
I z1 z a2 A; y1 y b2 A;
2dA
A
(y2
A
z2 )dA
IZ
Iy.
Izy
z y dA;
A
五、平行移轴公式:
I z1 z a2 A; y1 y b2 A;
I z1y1 I zy abA;
返回 下一张 上一张 小结
六、主惯性轴和主惯性矩: 主惯性轴（主轴）—使 I zoyo 0 的这对正交坐标轴； 主惯性矩（主惯矩）—截面对主惯性轴的惯性矩； 形心主惯性轴（形心主轴）—通过形心的主惯性轴； 形心主惯性矩（形心主惯矩）—截面对形心主轴的惯性矩。
I z1y1 I zy abA;
注意: y、z轴必须是形心轴。
二、转轴公式:
Iz1
A y12dA
( y cos z sin)2 dA;
A
I z1
Iz
Iy 2
Iz
Iy 2
cos 2
I zy
sin 2;
I y1
Iz
2
Iy
Iz
2
Iy
cos 2
I zy
sin 2;
I z1y1
Iz
Iy 2
三、惯性积:
定义:平面图形内, 微面积dA与其两个坐 标z、y的乘积zydA在整个图形内的积分称为 该图形对z、y轴的惯性积。
Izy
z y dA;
A
特点: ①惯性积是截面对某两个正交

第七章 截面的几何性质

第七章 截面的几何性质

A 120 ×10 × 60 + 70 ×10 × 5 = = 39.7mm 120 ×10 + 70 ×10
yc =
Sy
5
§7-2 惯性矩、惯性积与极惯性 惯性矩、
一、惯性矩
Iz = ∫ y dA
2 A
I y = ∫ z dA
2 A
工程中常把惯性矩表示为平面图形的面积与某一长度平方的乘积， 即
I y = A iy
主惯性轴和主惯性矩
一、主惯性轴和主惯性矩 (1)主惯性轴 主惯性轴 当平面图形对某一对正交坐标轴z0 、
y0的惯性积 Iz0y0=0时，则坐标轴 z0 、y0称为主惯性轴。 因此，具有一个或两个对称轴的正交坐标轴一定是 平面图形的主惯性轴。 (2)主惯性矩 平面图形对任一主惯性轴的惯性矩称为 主惯性矩 主惯性矩。
例 计算图所示阴影部分截面的形心主惯性矩Iz。
解：1)求形心位置 由于y 轴为对称轴，故形心必在 此轴上，建立yoz′坐标系，故zc′=0 。将阴影部分截面看成是矩形Ⅰ 减去圆形Ⅱ而得到，故其形心的yc 坐标为：
15
ΣAi y ci yc = =( A
600 × 1000 × 500 − 600 × 1000 −
2
I z = Aiz
2
6
i y 、i z
分别称为平面图形对y轴和z轴的惯性半径
二、惯性积
I zy = ∫ A zydA
若截面具有一根对称轴，则该 截面对于包括此对称轴在内的 二正交坐标轴的惯性积一定等 于零。
I zy = 0
7
三、极惯性矩
Ip =
2
∫A
ρ dA
2
2 2
Qρ = z + y

材料力学截面的几何性质课件

材料力学截面的几何性质课件
材料力学截面的几何 性质课件
目录
• 截面的基本性质 • 截面的二次矩 • 截面的抗弯截面系数 • 截面的抗扭截面系数 • 材料力学截面的应用
01 截面的基本性质
截面的面积
面积
截面面积是二维平面图形被截后，与 原图形相比增加的面积。对于矩形、 圆形、三角形等简单形状，截面面积 可以通过几何公式直接计算。
的刚度和稳定性。
截面惯性矩
截面惯性矩是衡量截面抗弯刚度 的指标，对于承受弯矩的构件， 选择具有较大惯性矩的截面可以
减少挠度和转角。
截面抵抗矩
截面抵抗矩是衡量截面抗剪切能 力的指标，对于承受剪力的构件 ，选择具有较大抵抗矩的截面可
以增加构件的承载能力。
工程设计中的应用
桥梁设计
在桥梁设计中，需要考虑梁的截面尺寸、材料类型和截面形式等 因素，以确保桥梁具有足够的强度和刚、单位等因素，以确保数 据处理结果的准确性和可靠性。
1.谢谢聆 听
根据微面积和其对应的主 轴方向余弦，计算出截面 二次矩。
主轴的确定
根据计算出的惯性矩，找 出三个主轴的方向余弦和 角度。
实例分析
圆截面
圆截面的二次矩为常数， 且各主轴与截面垂直，说 明圆截面在弯曲时没有翘 曲的趋势。
矩形截面
矩形截面的二次矩与宽度 的平方成正比，说明矩形 截面有较好的抗弯能力。
工字形截面
工字形截面的二次矩比同 样面积的矩形截面小，但 抗弯能力仍高于同样重量 的实心杆件。
03 截面的抗弯截面系数
定义与性质
01
抗弯截面系数是截面对其轴线的惯性矩除以截面的面积 得到的数值，用来度量截面在弯矩作用下抵抗变形的能 力。
02
不同形状的截面有不同的抗弯截面系数，如圆截面为1 ，矩形截面为1.13，工字形截面为1.44等。

截面的几何性质面积矩惯性矩惯性积平行移轴

截面的几何性质面积矩惯性矩惯性积平行移轴

2
对于复杂形状，可以采用微元法或积分法计算其 惯性矩。
3
在工程实践中，常常使用软件或计算器进行惯性 矩的计算，以提高计算效率和精度。
04
CATALOGUE
惯性积
惯性积的定义
惯性积是截面的一种几何属性，用于描述截面的 形状和大小。
惯性积是一个标量，表示截面在某个方向上的投 影面积与该方向上单位长度的平方之比。
02
利用三维坐标系中的点坐标和 方向向量，通过向量的外积计 算得到截面的法向量和面积向 量，进而计算惯性积。
03
利用计算机图形学中的几何算 法，通过计算截面的顶点坐标 和法线向量，实现惯性积的精 确计算。
05
CATALOGUE
平行移轴
平行移轴的定义
一个方向上的直线，可以 是实线或虚线。
在三维空间中，与某一平 面相交的平面。
中性轴
通过截面形心并与形心轴垂直的轴线。
惯性矩的性质
01
惯性矩与截面的形状和大小有关，形状相同但尺寸不同的截面 具有不同的惯性矩。
02
惯性矩具有方向性，与中性轴的位置有关。
对于矩形、圆形、椭圆形等简单形状，其惯性矩可以通过公式
03
直接计算。
惯性矩的计算方法
1
对于简单形状，如矩形、圆形、椭圆形等，可以 直接使用公式计算其惯性矩。
截面的几何性质
目录
• 截面的定义与性质 • 面积矩 • 惯性矩 • 惯性积 • 平行移轴
01
CATALOGUE
截面的定义与性质
截面的定义
截面定义
截面是指通过一个平面与一个三维物 体相交，所形成的交线或交面。这个 平面可以是垂直的、倾斜的或与三维 物体表面平行。
截面的形状

建筑力学第七章 截面的几何性质

建筑力学第七章 截面的几何性质

第七章平面图形的几何性质研究截面几何性质的意义从上章介绍的应力和变形的计算公式中可以看出，应力和变形不仅与杆的内力有关，而且与杆件截面的横截面面积A、极惯性矩I P、抗扭截面系数W P等一些几何量密切相关。

因此要研究构件的的承载能力或应力，就必须掌握截面几何性质的计算方法。

另一方面，掌握截面的几何性质的变化规律，就能灵活机动地为各种构件选取合理的截面形状和尺寸，使构件各部分的材料能够比较充分地发挥作用，尽可能地做到“物尽其用”，合理地解决好构件的安全与经济这一对矛盾。

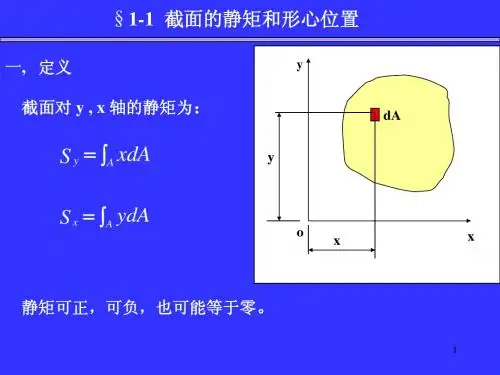
第一节 静矩一、静距的概念Ay S z d d =Az S y d d =⎰⎰⎰⎰====AAy y AAz z Az S S A y S S d d d d zy d A yz静距是面积与它到轴的距离之积。

平面图形的静矩是对一定的坐标而言的，同一平面图形对不同的坐标轴，其静矩显然不同。

静矩的数值可能为正，可能为负，也可能等于零。

它常用单位是m 3或mm 3。

形心d A zyy zCx Cy ⎪⎪⎭⎪⎪⎬⎫⋅∆∑=⋅∆∑=A y A y Az A z C C ⎪⎪⎭⎪⎪⎬⎫==⎰⎰A ydA y A zdA z AC A C ⎪⎪⎭⎪⎪⎬⎫==A S y A S z z C y C ⎭⎬⎫⋅=⋅=C y C z z A S y A S 平面图形对z 轴（或y 轴）的静矩，等于该图形面积A 与其形心坐标y C （或z C ）的乘积。

当坐标轴通过平面图形的形心时，其静矩为零；反之，若平面图形对某轴的静矩为零，则该轴必通过平面图形的形心。

如果平面图形具有对称轴，对称轴必然是平面图形的形心轴，故平面图形对其对称轴的静矩必等于零。

⎭⎬⎫⋅=⋅=C y C z z A S y A S二、组合图形的静矩根据平面图形静矩的定义，组合图形对z 轴（或y 轴）的静矩等于各简单图形对同一轴静矩的代数和，即⎪⎪⎭⎪⎪⎬⎫=+++==+++=∑∑==ni Ci i Cn n C C y ni Ci i Cn n C C z z A z A z A z A S y A y A y A y A S 1221112211 式中 y Ci 、z Ci 及A i 分别为各简单图形的形心坐标和面积;n 为组成组合图形的简单图形的个数。

截面的几何性质

截面的几何性质
I x = I xc + a A
2
= I y + b2 A Iy
c
37
4. 组合截面惯性矩
I x = ∑I xi
i=1
n
I y = ∑I yi
i=1
n
38

A y1 + A2 y2 1 y= ≈ 40mm A + A2 1
10
y
10
40
10
o
20
x
80
11
§1—2 极惯性矩 惯性矩
一，定义 1，截面对 o 点的极惯性矩为 ，
y
惯性积
dA
I P = ∫A ρ dA
2
ρ
o
x
12
2，截面对 x , y 轴的惯性矩 ，
y
I x = ∫A y dA
2
dA
= ∫A x2dA Iy
29
y
yC
C
xC
a
o
b
x
则平行移轴公式为
= I xc + a2 A Ix
= I y + b2 A Iy
c
I xy = I x y + abA
c c
30
二，组合截面的惯性矩
惯性积
Ixi , Iyi , Ixyi —— 第 i 个简单截面对 x , y 轴的惯性矩、
惯性积。 惯性积。
组合截面的惯性矩， 组合截面的惯性矩，惯性积
xC
a
o
b
x
Ix , Iy , Ixy
_____
轴的惯性矩和惯性积。 截面对 x , y 轴的惯性矩和惯性积。
的惯性矩和惯性积。 Ixc ,Iyc , Ixc yc —— 截面对形心轴 xc , yc 的惯性矩和惯性积。

材料力学 3 截面的几何性质


大小：正，负，0。
y
量纲：[长度]3
二、截面的形心 几何形心=等厚均质薄片重心 z 形心坐标公式：
yc
C
zc
yc zc
y dA A z dA
A
A
Sz A Sy A
O
A
y
S y A zc
S z A yc
结论： 若 S z 0 yc 0 z 轴通过形心。反之，亦成立。
转轴公式
sin 2 I yz cos2
I y1 I z1 I y I z
二、形心主轴和形心主惯性矩 1、主轴和主惯性矩：坐标旋转到= 0 时，
Ix y
0 0
Ix I y 2
sin20 I xy cos 20 0
tan 2 0
2 I xy Ix Iy
z1
I yzc y1 z1 dA
A
a
O
z
yc
I z A y 2dA A (b y1 )2 dA
2 A ( y1 2by1 b 2 )dA
y
zc 为形心轴， S zc Ayc 0
I zc 2bS zc b 2 A
I zc b 2 A
2


a
2677710 .52 cm 4
平 衡 项 惯 性 矩 6686481 . 857.8 单 个 形 心 惯 性 矩 779.53
组合截面可以大大提高截面惯性矩。
I y Iz 2 cos2 I yz sin 2 cos2 I yz sin 2
I y Iz 2
I y Iz 2
当＝0时，
dI y1 d

截面的几何性质


b2
A
上式称为计算惯性矩的平行移轴公式。这个公式表明 ：截面对任意一个轴的惯性矩，等于截面对与该轴平行的 形心轴的惯性矩加上截面的面积与两轴距离的乘积。
工程力学与建筑结构
1.4 组合截面的惯性矩
在计算组合截面对某座标轴的惯性矩时，根据定义， 可分别计算各组成部分对该轴的惯性矩，然后再相加，即 ：
工程力学与建筑结构
工程力学与建筑结构
截面的几何性质
在工程中研究构件的受力和变形时，经常会遇到一些 和构件的横截面形状、尺寸有关的几何量，这些几何量通 称为截面的几何性质。 1.1 截面的静矩和形心 1. 截面的静矩
如图所示的平面图形代表一个任意截面，其面积为A 。在图形平面内选坐标系Oyz，在坐标为(y, z)处取微面积 dA ，则以下两个积分分别被定义为平面图形A 对于z轴和y 轴的静矩。
I z iz2 A
Iy
i
2 y
A
于是得到:
iz
Iz A
iy
IyБайду номын сангаасA
通常把iz和iy分别称为平面图形对z轴和y轴的惯性半径 （或回转半径）。
工程力学与建筑结构
1.3平称移轴公式 同一截面对于不同坐标轴的惯性矩不相同， 但它们
之间都存在着一定的关系。
I z I zc a 2 A
Iy
I yc
Ai
i 1
工程力学与建筑结构
1.2 截面的惯性矩 1. 惯性矩的计算公式
任意一个构件的横截面如图所示，其面积A 对于z轴和 y轴的惯性矩定义为 ：
I z
A
y 2dA
I y
z 2dA
A
常用截面的惯性矩可查阅工程设计手册。
工程力学与建筑结构

材料力学第四章截面的几何性质

确定截面的剪切中心
在材料力学中，剪切中心是剪切应力作用下截面 发生剪切变形的点。通过计算截面的形心，可以 近似确定剪切中心的位置。
确定截面的质心
质心是截面质量的中心点，通过计算截面的形心， 可以近似确定质心的位置，这对于动力学分析和 稳定性分析非常重要。
03 主轴和主惯性矩
主轴的定义与计算
主轴
截面上的各点处到截面形心距离最大的方向。
预测物体的变形和破坏
通过分析截面的几何性质，可以预测 物体在不同受力条件下的变形和破坏 行为，为工程实践提供指导。
02 截面的面积和形心
截面面积的定义与计算
截面面积的定义
截面面积是指通过截面边界轮廓 线围成的区域面积。
截面面积的计算
可以通过测量截面轮廓线的长度 ，然后使用公式计算面积。对于 不规则形状，可以使用微元法或 积分法计算。
截面几何性质的应用前景
随着科技的发展和工程需求的提高，截面几何性质在材料力学中的重要性将更加凸 显，其在航空航天、交通运输、建筑等领域的应用将更加广泛。
随着新型材料的不断涌现，截面几何性质的研究将有助于深入了解这些材料的力学 行为，为新型材料的优化和应用提供理论支持。
随着数值模拟和计算机技术的发展，截面几何性质的研究将更加精确和深入，有助 于提高工程结构的分析和设计水平。
在实际工程中，主轴和主惯性矩也是 进行有限元分析时的重要输入参数， 用于模拟结构的力学行为并优化设计。
在结构设计时，根据主轴和主惯性矩 可以合理地选择材料的类型和截面的 形状，以提高结构的刚度和稳定性。
04 极惯性矩和惯性积
极惯性矩的定义与计算
极惯性矩
截面对任意直径的极惯性矩等于截面 面积与该直径的平方的乘积。
截面是确定物体受力分布和变形程度 的关键因素，通过研究截面的几何性 质，可以深入了解物体的力学性能， 为工程设计和安全评估提供依据。

《工程力学》课件第6章 截面图形的几何性质


Ip
r2dA A
D 2
r2
2
rdr
D4
0
32
Ip Iy Iz
Iy
பைடு நூலகம்
Iz
Ip 2
D4
64
四、组合截面的惯性矩与惯性积
z
I
例如工字型截面 A AI AII AIII
II
y
III
Iy
z 2 dA
A
z2dA z2dA z2dA
AI
AII
AIII
m
I yI I yII I yIII I yi
包括：形心、静矩、极惯性矩、惯性矩、惯性半径、惯 性积、主轴和形心主轴、主矩和形心主矩等
6.1 静矩和形心
一、静矩
截面对z轴的静矩
z
Sz
ydA
A
截面对y轴的静矩
y
dA
A
z
Sy
zdA
A
o
单位： m3
y
静矩的数值可大于零、等于零或小于零。
二、形心
如图所示均质薄板，重心与形心C重合，
由静力学可知形心坐标在yoz：
何关系， y R sin , dy R cosd ,
dA 2R cosdy 2R2 cos2 d
Sz
A
（2）形心
ydA yC
2 0
Sz A
R sin 2R2 cos2 d
2 R3 3
4R
1 R2 3
zC
2 3
0
R3
2
三、组合截面的静矩和形心 z
D d
y
整个图形对某一轴的静矩等于各个分图形对同一轴的静矩之和。
z1
y1 z
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

附录Ⅰ 截面的几何性质§I −1 截面的静矩和形心位置如图I −1所示平面图形代表一任意截面，以下两积分⎪⎭⎪⎬⎫==⎰⎰A z S A y S A y Az d d （I −1） 分别定义为该截面对于z 轴和y 轴的静矩。

静矩可用来确定截面的形心位置。

由静力学中确定物体重心的公式可得⎪⎪⎭⎪⎪⎬⎫==⎰⎰A A z z A A y y AC A Cd d利用公式（I −1），上式可写成⎪⎪⎭⎪⎪⎬⎫====⎰⎰A S A A z z A S A Ay y y AC z AC d d （I −2） 或⎭⎬⎫==C y C z Az S Ay S （I −3）⎪⎪⎭⎪⎪⎬⎫==A S z A S y y C z C （I −4）如果一个平面图形是由若干个简单图形组成的组合图形，则由静矩的定义可知，整个图形对某一坐标轴的静矩应该等于各简单图形对同一坐标轴的静矩的代数和。

即：⎪⎪⎭⎪⎪⎬⎫==∑∑==ni ci i y ni ci i z z A S y A S 11（I −5）式中A i 、y ci 和z ci 分别表示某一组成部分的面积和其形心坐标，n 为简单图形的个数。

将式（I −5）代入式（I −4），得到组合图形形心坐标的计算公式为图I −1⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎬⎫==∑∑∑∑====n i i ni ci i c ni i ni ci i c A z A z A y A y 1111 （I −6） 例题I −1 图a 所示为对称T 型截面，求该截面的形心位置。

解：建立直角坐标系zOy ，其中y 为截面的对称轴。

因图形相对于y 轴对称，其形心一定在该对称轴上，因此z C =0，只需计算y C 值。

将截面分成Ⅰ、Ⅱ两个矩形，则A Ⅰ=0.072m 2，A Ⅱ=0.08m 2 y Ⅰ=0.46m ，y Ⅱ=0.2m m323.008.0072.02.008.046.0072.0III IIII I I 11=+⨯+⨯=++==∑∑==A A y A y A AyA y ni ini cii c§I −2 惯性矩、惯性积和极惯性矩如图I −2所示平面图形代表一任意截面，在图形平面内建立直角坐标系zOy 。

现在图形内取微面积d A ，d A 的形心在坐标系zOy 中的坐标为y 和z ，到坐标原点的距离为ρ。

现定义y 2d A 和z 2d A 为微面积d A 对z 轴和y 轴的惯性矩，ρ2d A 为微面积d A 对坐标原点的极惯性矩，而以下三个积分⎪⎪⎭⎪⎪⎬⎫===⎰⎰⎰A ρI A z I A y I A Ay A z d d d 2P 22 （I −7） 分别定义为该截面对于z 轴和y 轴的惯性矩以及对坐标原点的极惯性矩。

由图（I −2）可见，222z y +=ρ，所以有⎰⎰+=+==Ayz AI I A z y A ρI )d (d 222P （I −8）即任意截面对一点的极惯性矩，等于截面对以该点为原点的两任意正交坐标轴的惯性矩之和。

另外，微面积d A 与它到两轴距离的乘积zy d A 称为微面积d A 对y 、z 轴的惯性积，而积分Azyd I Ayz ⎰=（I −9）定义为该截面对于y 、z 轴的惯性积。

例题I −1图图I −2从上述定义可见，同一截面对于不同坐标轴的惯性矩和惯性积一般是不同的。

惯性矩的数值恒为正值，而惯性积则可能为正，可能为负，也可能等于零。

惯性矩和惯性积的常用单位是m 4或mm 4。

§I −3 惯性矩、惯性积的平行移轴和转轴公式一、惯性矩、惯性积的平行移轴公式图I −3所示为一任意截面，z 、y 为通过截面形心的一对正交轴，z 1、y 1为与z 、y 平行的坐标轴，截面形心C 在坐标系z 1O y 1中的坐标为（b ，a ），已知截面对z 、y 轴惯性矩和惯性积为I z 、I y 、I yz ，下面求截面对z 1、y 1轴惯性矩和惯性积I z 1、I y 1、I y 1z 1。

Aa I I z z 21+=（I −10）同理可得Ab I I y y 21+=（I −11）式（I −10）、（I −11）称为惯性矩的平行移轴公式。

下面求截面对y 1、z 1轴的惯性积11z y I 。

根据定义⎰⎰++==AAz y Aa yb z A y z I )d )((d 1111⎰⎰⎰⎰+++=AAAAAab A y b A z a A zy d d d dabA bS aS Izy yz +++= 由于z 、y 轴是截面的形心轴，所以S z =S y =0，即abAI Iyz z y +=11 （I −12）式（I −12）称为惯性积的平行移轴公式。

二、惯性矩、惯性积的转轴公式图（I −4）所示为一任意截面，z 、y 为过任一点O 的一对正交轴，截面对z 、y 轴惯性矩I z 、I y 和惯性积I yz 已知。

现将z 、y 轴绕O 点旋转α角（以逆时针方向为正）得到另一对正交轴z 1、y 1轴，下面求截面对z 1、y 1轴惯性矩和惯性积1z I、1y I 、11z y I 。

图I −3αα2sin 2cos 221yz yz yz z I I I I I I --++=（I −13）同理可得αα2sin 2cos 221yz yz yz y I I I I I I +--+=（I −14）αα2cos 2sin 211yz yz z y I I I I +-=（I −15）式（I −13）、（I −14）称为惯性矩的转轴公式，式（I −15）称为惯性积的转轴公式。

§I −4 形心主轴和形心主惯性矩一、主惯性轴、主惯性矩由式（I −15）可以发现，当α=0o，即两坐标轴互相重合时，yzz y I I =11；当α=90o时，yz z y II -=11，因此必定有这样的一对坐标轴，使截面对它的惯性积为零。

通常把这样的一对坐标轴称为截面的主惯性轴，简称主轴，截面对主轴的惯性矩叫做主惯性矩。

假设将z 、y 轴绕O 点旋转α0角得到主轴z 0、y 0，由主轴的定义2cos 2sin 20000=+-=ααyz yz z y I I I I从而得y z yz II I α--=22tan 0 （I −16）上式就是确定主轴的公式，式中负号放在分子上，为的是和下面两式相符。

这样确定的α0角就使得0z I等于m ax I。

由式（I −16）及三角公式可得2204)(2cos yzy z yz I I I I I +--=α2204)(22sin yzy z yzI I I I +--=α将此二式代入到式（I −13）、（I −14）便可得到截面对主轴z 0、y 0的主惯性矩⎪⎪⎭⎪⎪⎬⎫+--+=+-++=22224)(2124)(21200yzy z y z y yzy z yz z I I I I I I I I I I I I （I −17）二、形心主轴、形心主惯性矩通过截面上的任何一点均可找到一对主轴。

通过截面形心的主轴叫做形心主轴，截面对形心主轴的惯性矩叫做形心主惯性矩。

例题I −5 求例I −1中截面的形心主惯性矩。

解：在例题I −1中已求出形心位置为=C z ，m323.0=C y过形心的主轴z 0、y 0如图所示，z 0轴到两个矩形形心的距离分别为m 137.0I =a ，m 123.0II =a截面对z 0轴的惯性矩为两个矩形对z 0轴的惯性矩之和，即2IIII II 2I I I II I 0a A I a A I I z z z +++=2323123.04.02.0124.02.0137.012.06.01212.06.0⨯⨯+⨯+⨯⨯+⨯=42m 1037.0-⨯=截面对y 0轴惯性矩为4233II I m 10242.0122.04.0126.012.000-⨯=⨯+⨯=+=y y y III第六章 梁的应力§6−1 梁的正应力一、纯弯曲与平面假设本节将推导梁弯曲时横截面上正应力的计算公式。

为了方便，我们先研究梁横截面上只有弯矩的情况，这种情况称为“纯弯曲”。

如图6−1所示的梁，在如图所示荷载作用下，中间CD 段就属于这种情况，由其剪力图和弯矩图可以看到，在CD 段内的弯矩M =Fa =常数，而剪力F S 等于零。

我们先作如下的实验，观察到如下的一些现象：（1）变形前，梁侧面上与纵向直线垂直的横向线在变形后仍为直线，并且仍然与变形后的梁轴线（简称挠曲线）保持垂直，但相对转过一个角度。

（2）变形前互相平行的纵向直线，变形后均变为圆弧线，并且上部的纵线缩短，下部的纵线伸长。

在梁中一定有一层上的纤维既不伸长也不缩短，此层称为中性层。

中性层与梁横截面的交线称为中性轴。

根据这些实验现象，我们对纯弯曲情况下作出如下假设： 1.平面假设：梁的横截面在梁弯曲后仍然保持为平面，并且仍然与变形后的梁轴线保持垂直。

2.单向受力假设：梁的纵向纤维处于单向受力状态，且纵向纤维之间的相互作用可忽略不计。

二、正应力公式的推导1相应的纵向线应变为ρρεy x xy x ==d d (6−1) M 图图6−1 (a) (b)(c)(b) 图6−2 图6−3中性层中性轴(b)abO 1 O2mnp q(a)mn p q(c)2式（6−1）表明：梁的纵向纤维的应变与纤维距中性层的距离成正比，离中性层愈远，纤维的线应变愈大。

2．物理方面在弹性范围内正应力与线应变的关系为εE σ=将式（6−1）代入，得ρyEσ= （6−2）3．静力学方面由图6−4可以看出，梁横截面上各微面积上的微内力d F N =σd A 构成了空间平行力系，它们向截面形心简化的结果应为以下三个内力分量⎰=A AσF d N ，⎰=A y A σz M d ，⎰=A z Aσy M d由截面法可求得该截面上只有弯矩M ，即上式中F N ，M y 均等于零，所以有d N ==⎰A A σF （d ） 0d ==⎰Ay A σz M （e ）MA σy M Az ==⎰d（f ）由式（d ）得d d N ===⎰⎰A AρAEy A σF因E 、ρ为常量，所以有d ==⎰z AS A y （g ）即梁横截面对中性轴（z 轴）的静矩等于零。

由此可知，中性轴通过横截面的形心，于是就确定了中性轴的位置。

由式（e ）可得0d d d ====⎰⎰⎰AA Ay A zy ρEA ρEzy A σz M因此d ==⎰yz AI A zy （h ）即梁横截面对y 、z 轴的惯性积等于零，说明y 、z 轴应为横截面的主轴，又y 、z 轴过横截面的形心，所以其应为横截面的形心主轴。

最后由式（f ）可得MA σy M Az ==⎰d即A 图6−4ρρρσzAAAEI A y EA Ey A y M ====⎰⎰⎰d d d 22式中⎰=Az Ay I d 2是梁横截面对中性轴的惯性矩。