1第一章 连续时间信号分析

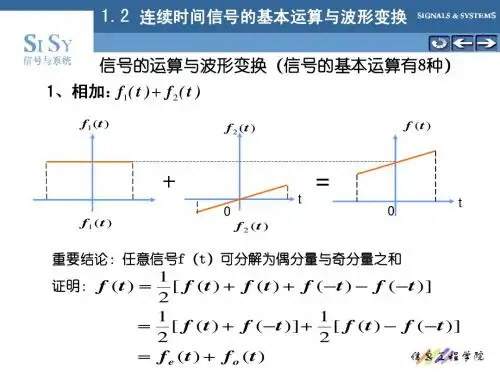
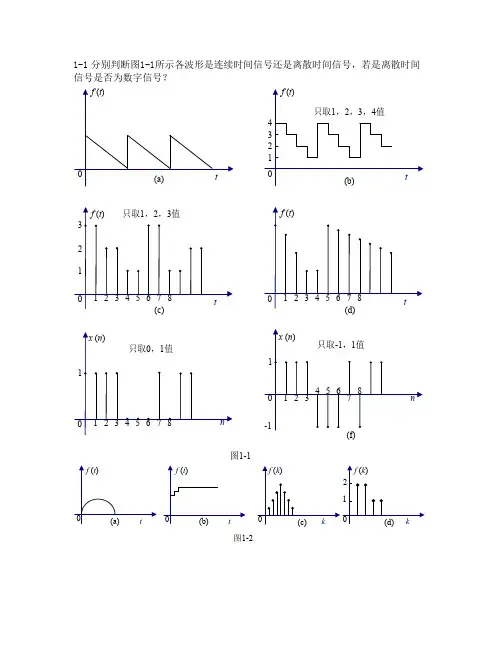
1-1分别判断图1-1所示各波形是连续时间信号还是离散时间信号，若是离散时间信号是否为数字信号？图1-1图1-2解 信号分类如下：图1-1所示信号分别为⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--））（散（例见图数字：幅值、时间均离））（连续（例见图抽样：时间离散，幅值离散））（连续（例见图量化：幅值离散，时间））（续（例见图模拟：幅值、时间均连连续信号d 21c 21b 21a 21（a ）连续信号（模拟信号）；（b ）连续（量化）信号；（c ）离散信号，数字信号；（d ）离散信号；（e ）离散信号，数字信号；（f ）离散信号，数字信号。

1-2 分别判断下列各函数式属于何种信号？（重复1-1题所示问）（1）；)sin(t e at ω-（2）；nT e -（3）；)cos(πn （4）；为任意值）（00)sin(ωωn （5）。

221⎪⎭⎫ ⎝⎛解由1-1题的分析可知：（1）连续信号；（2）离散信号；（3）离散信号，数字信号；（4）离散信号；（5）离散信号。

1-3 分别求下列各周期信号的周期T ：（1）；)30t (cos )10t (cos -（2）；j10t e （3）；2)]8t (5sin [（4）。

[]为整数）（n )T nT t (u )nT t (u )1(0n n ∑∞=-----解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号，需要考察各分量信号的周期是否存在公倍数，若存在，则该复合信号的周期极为此公倍数；若不存在，则该复合信号为非周期信号。

（1）对于分量cos (10t )其周期；对于分量cos (30t )，其周期。

由于5T 1π=15T 2π=为的最小公倍数，所以此信号的周期。

5π21T T 、5T π=（2）由欧拉公式)t (jsin )t (cos e t j ωωω+=即)10t (jsin )10t (cos e j10t +=得周期。

5102T ππ==（3）因为[])16t (cos 2252252)16t (cos 125)8t (5sin 2-=-⨯=所以周期。

信号与系统第一章1。

1 连续时间与离散时间信号确知信号可以表示成一个或几个自变量的函数连续时间信号在［t1，t2］区间的能量定义为：连续时间信号在［t1,t2］区间的平均功率定义为：离散时间信号在［n1,n2］区间的能量定义为离散时间信号在[n1，n2]区间的平均功率为在无限区间上也可以定义信号的总能量：连续时间情况下:离散时间情况下:在无限区间内的平均功率可定义为： 21lim 2()TTT P dtTx t ∞-→∞=⎰能量信号——信号具有有限的总能量，即：功率信号—-信号有无限的总能量,但平均功率有限。

即：信号的总能量和平均功率都是无限的。

即:如果信号是周期信号，则或这种信号也称为功率信号，通常用它的平均功率来表征或或如果信号是非周期的，且能量有限则称为能量信号。

1.2 自变量的变换1.时移变换当时，信号向右平移时，信号向左平移当时，信号向右平移 时，信号向左平移,0E P ∞∞<∞=,E P ∞∞=∞=∞2。

反转变换信号以t=0为轴呈镜像对称。

与连续时间的情况相同。

3. 尺度变换时，是将在时间上压缩a倍,时,是将在时间上扩展1/a倍。

由于离散时间信号的自变量只能取整数值，因而尺度变换只对连续时间信号而言。

周期信号与非周期信号：周期信号：满足此关系的正实数（正整数)中最小的一个，称为信号的基波周期（）。

可视为周期信号，但它的基波周期没有确定的定义。

可以视为周期信号,其基波周期。

奇信号与偶信号：对实信号而言：如果有和则称该信号是偶信号。

（镜像偶对称）如果有和则称该信号为奇信号。

(镜像奇对称）对复信号而言：如果有和则称该信号为共轭偶信号.如果有和则称为共轭奇信号。

任何信号都能分解成一个偶信号与一个奇信号之和。

对实信号有：其中其中对复信号有：其中：其中：1。

3 复指数信号与正弦信号一. 连续时间复指数信号与正弦信号其中C, a 为复数1. 实指数信号：C,a 为实数呈单调指数上升呈单调指数下降。

（一）连续时间信号的时域表示信号是消息的载体，是消息的一种表现形式。

信号可以是多种多样的，通常表现为随时间变化的某些物理量，一般用x(t)或x(n)来表示。

信号按照自变量的取值是否连续可分为连续时间信号和离散时间信号。

连续时间信号是指自变量的取值范围是连续的，且对于一切自变量的取值，除了有若干不连续点以外，信号都有确定的值与之对应。

严格来说，MATLAB并不能处理连续信号，而是用等时间间隔点的样值来近似地表示连续信号。

当取样时间间隔足够小时，这些离散的样值就能较好地近似连续信号。

在MATLAB中通常用向量来表示连续时间信号，向量需要与时间变量相对应。

对于连续时间信号x(t)，可用x、t两个行向量来表示。

其中向量t是形如t=t1:p:t2的MATLAB命令定义的时间范围向量，t1为信号起始时间，t2为终止时间，p为时间间隔。

向量x为连续信号x(t)在向量t所定义的时间点上的样值。

如产生连续信号t ttSa tx)sin( )()(==可用如下命令实现：t =-10:1.5:10;x=sin(t)./ t;在命令窗口（Command Window）中可得到程序执行的结果即x、t的具体值。

注意：在MATLAB程序调试过程中，有时程序执行不出结果或虽然出结果但存在一些问题，MATLAB 都会在Command窗口中给出错误说明，掌握利用Command窗口中的说明检查程序的方法。

用上述向量对连续信号进行表示后，就可以用plot命令绘制信号的时域波形。

命令如下：plot(t,x)title(‘x(t)=Sa(t)’)xlabel(‘t’)axis([-10,10,-0.2,1.2])绘制的信号波形如图一所示，当把t改为：t =-10:0.5:10;则可得到图二。

因为plot命令将点与点之间用直线连接，当点与点之间距离很小时，绘出的图形就成了光滑的曲线。

但图二在t=0时，曲线是间断的。

图一 图二应用plot 函数时应确保自变量t 和函数值x 的个数相等；函数axis([x1,x2,y1,y2])用来对横纵坐标进行限定，以完善图形，其中x1和x2分别为横坐标的起始和截止位置，y1和y2分别为纵坐标的起始和截止位置； xlabel(‘’)、ylabel(‘’)和title(‘’)用于为该图添加横、纵坐标说明和标题；有时在一个程序中需要将几个图形绘制在一个窗口，利用subplot(m,n,k)函数可以将当前窗口分成m 行n 列个子窗口，并在第k 个子窗口绘图，窗口的排列顺序为从左至右，从上至下分别为1,2,…m*n 。

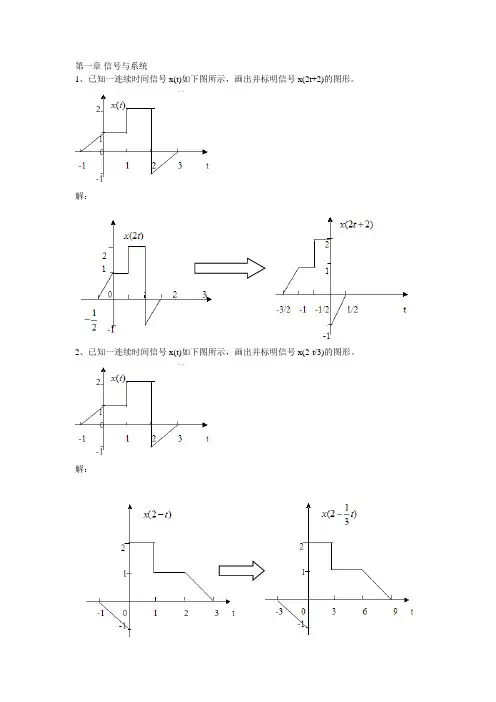
第一章信号与系统1、已知一连续时间信号x(t)如下图所示，画出并标明信号x(2t+2)的图形。

解：2、已知一连续时间信号x(t)如下图所示，画出并标明信号x(2-t/3)的图形。

解：3、画出信号te tf -=)(，+∞<<∞-t 的波形。

解：由题意知,0(),0t te tf t e t -⎧≤<∞⎪=⎨-∞<<⎪⎩由此绘出波形4、画出信号)(sin )(t t f ε=的波形，其中)()(t t t r ε=为斜升函数。

解：由()t ε定义，可知当sin 0t >时，()1f t =；sin 0t <时，()0f t =。

先画出sin t 的波形，再根据响应的时间区域绘出()(sin )f t g t =的波形，如下图所示()(sin )f t tε=5、画出信号)()1()(k k k f ε+=的波形，其中)()(t t t r ε=为斜升函数。

解：根据)(k ε的定义，可将)(k f 写为⎩⎨⎧<≥+=0,00,1)(k k k t f ，由此绘其波形如下图所示6、画出信号)2()1(3)1(2)(-+--+=t t t t f εεε的波形，其中)()(t t t r ε=为斜升函数。

解：由时移阶跃函数的特点，知⎪⎪⎩⎪⎪⎨⎧><<-<<--<=2,021,111,21,0)(t t t t t f，由此绘其波形，如下图所示7、画出信号=)(k f 2)2(--k ε(k-2)的波形，其中)()(t t t r ε=为斜升函数。

解：⎩⎨⎧<≥=--2,02,2)()2(k k k f k ，8、写出下图所示波形的表达式。

解：)(t f 是阶梯波形，从左到右有三个跃变时间点，则可推知)(t f 是由三个阶跃函数构成，并且向上跳跃阶跃函数的系数为正，向下跳跃阶跃函数的系数为负，跳跃幅值决定系数的值的大小，据此，图中)(t f 的表达式为)2()1()1(2)(----+=t t t t f εεε 9、写出下图所表示序列的闭合形式表达式。

实验一 连续时间信号§1.2 连续时间复指数信号 基本题1．对下面信号创建符号表达式()()t t t x ππ2c o s2sin )(= 这两个信号应分别创建，然后用symmul 组合起来。

对于T=4，8和16，利用ezplot 画出320≤≤t 内的信号。

什么是)(t x 的基波周期？x(t) =cos((pi*t)/2)*sin((pi*t)/2)=1/2sin(pi*t) (T=4)若令f1=1 /T1=1/2,很容易得到其基波分量：1/2sin(pi*t)同理可得：x(t)=cos((pi*t)/4)*sin((pi*t)/4)=1/2sin((pi*t)/2) (T=8)其基波分量为1/2sin((pi*t)/2),基频为f1=1/T1=1/4x(t)= cos((pi*t)/8)*sin((pi*t)/8)=1/2sin((pi*t)/4) (T=16)其基波分量为1/2sin((pi*t)/4)，基频为f1=1/T1=1/8 中等题2．对下面信号创建一个符号表达式()t e t x at π2cos )(-=对于81,41,21=a ，利用ezplot 确定d t ，d t 为)(t x 最后跨过0.1的时间，将d t 定义为该信号的消失的时间。

利用ezplot 对每一个a 值确定在该信号消失之前，有多少个完整的余弦周期出现，周期数目是否正比于品质因素a T Q 2)2(π=？1）当a=1/2时： x(t)= cos(2*pi*t)/exp(t/2)利用Tool菜单中的data cursor项目可大致确定d t=4.548在该信号消失之前，有个约4(4.5)完整的余弦周期出现，对应的品质因数为6.28。

2）当a=1/4时： x(t)= cos(2*pi*t)/exp(t/4)利用Tool菜单中的data cursor项目可大致确定d t=9.053在该信号消失之前，有个约9完整的余弦周期出现，对应的品质因数为12.57。

习题11.1 判断题1.1图所示各信号的波形是连续时间信号还是离散时间信号？若是连续时间信号是否为模拟信号？若是离散时间信号是否为数字信号？(1)(2)(3) (4)题1.1图 信号波形解:（1）时间连续函数值连续，连续时间信号，模拟信号（2）时间连续函数值离散，连续时间信号，不是模拟信号 （3）时间离散函数值离散量化，离散时间信号，数字信号 （4）时间离散函数值非量化，离散时间信号，不是数字信号1.2 判断以下各信号是能量信号还是功率信号？是周期信号还是非周期信号？若是周期信号，试求出其周期T 。

（1）sin()atet ω-()t ε （2）cos(10)cos(30)t t + （3）cos(2)sin()t t π+（4）25sin (8)t （5）()(10)t t εε-- （6）10()()200n n x n n ⎧≥⎪=⎨<⎪⎩解:（1）只在大于零的时间段内有信号，非周期信号；判断能量值若0a >则为指数衰减信号为能量信号。

()()()()22-022001cos 2sin d d 21d cos 2d 2at atat at t W e t t t e t e t e t t ωωεω∞∞--∞∞∞---==⎡⎤=-⎢⎥⎣⎦⎰⎰⎰⎰22011d 022at ate t e aa ∞--∞-==⎰()()()()()()()()()()()2222220002200222211cos 2d d +d 2211122212142a j t a j t at at j t j ta j t a j t e t t e e e t e e t e e a j a j a a a a ωωωωωωωωωωω∞∞∞---+------+∞∞=+=⎡⎤=+⎢⎥---+⎣⎦-=-=++⎰⎰⎰()()()22002222221d cos 2d 21122224atat W e t e t t a a a a a a ωωωω∞∞--⎡⎤=-⎢⎥⎣⎦⎡⎤+⎢⎥=-=++⎢⎥⎣⎦⎰⎰ （2）cos(10)cos(30)t t +15T π=215T π=则为周期信号5T π=时间上无限延续，则判断功率[]T dt t t t t dtt t t t dt t x p T T T T T T =⎥⎦⎤⎢⎣⎡+++++=++==⎰⎰⎰---222222222121)60cos()20cos()40cos(21)20cos()30(cos )30cos()10cos(2)10(cos )(余弦信号在一个周期内积分为零。

连续时间信号的分析讲义在信号与系统领域中，连续时间信号是一种在实数域上定义的信号，其取值在连续的时间范围内变化。

连续时间信号的分析是信号与系统学习的重要基础，本讲义将介绍连续时间信号的分析方法。

二、连续时间信号的基本概念1. 连续时间信号的定义：连续时间信号是在连续的时间范围上定义并取值的信号。

2. 连续时间信号的特性：- 幅度：信号在每个时间点的取值。

- 相位：信号波形相对于给定参考点（通常为时间轴原点）的相对位置。

- 周期性：信号在某个时间间隔内是否重复。

- 能量与功率：信号能量的大小及其在单位时间内消耗的能量。

三、连续时间信号的表示方法1. 数学表达：- 函数表达：通过一个函数来描述信号在每个时间点的取值。

- 积分表达：信号可以表示为另一个函数的积分形式。

2. 图形表示：- 时域图：横轴表示时间，纵轴表示信号幅度，用连续的曲线表示信号波形。

- 频谱图：横轴表示频率，纵轴表示幅度，用柱状图表示信号的频率分量及其幅度。

四、连续时间信号的常见类型1. 基本连续时间信号：- 典型脉冲信号：矩形脉冲、三角脉冲等。

- 正弦信号：包括正弦波、余弦波及其复合形式。

2. 周期性信号：具有重复性质的信号，可以表示为基本连续时间信号的线性组合。

3. 非周期性信号：不具有重复性质的信号，不能表示为基本连续时间信号的线性组合。

五、连续时间信号的分析方法1. 时域分析：分析信号在时间域上的特性，包括信号的幅度、相位和波形等。

- 平均值和均方值：描述信号的幅度特性。

- 时域波形图分析：通过观察信号的图像，了解信号的频率和幅度变化等特性。

2. 频域分析：分析信号在频率域上的特性，揭示信号的频率分量及其幅度。

- 傅里叶变换：将信号从时域转换为频域，得到信号的频谱信息。

- 频率响应：用于描述系统对不同频率信号的响应特性。

3. 其他分析方法：包括奇偶性分析、对称性分析、函数积分等。

六、连续时间信号的实际应用连续时间信号的分析方法在信号处理、通信系统、音频处理等领域有着广泛的应用。