信号与系统第四章练习题

其拉氏逆变换为： s3 + s 2 + 1 f (t ) = F [ ] = (-e-2t + 2e -4t )U (t ) ( s + 1)( s + 2)
-1
(8)
s+5 s ( s 2 + 2 s + 5) s+5 A B1s + B2 = = + s[( s + 1)2 + 4] s ( s + 1)2 + 4 A= s+5 gs = 1 s[( s + 1) 2 + 4)] s =0
(3) (2 cos t + sin t )U (t ) 查表得： s s + w2 w sin wtU (t ) « 2 s + w2 \ 根据拉氏变换的线性性质： 2s 1 2s + 1 (2 cos t + sin t )U (t ) « 2 + 2 = 2 s +1 s +1 s +1 cos wtU (t ) «
(9) 2d (t - t0 ) + 3d (t ) 根据时移特性：
d (t - t0 ) « e - st0
\ 2d (t - t0 ) + 3d (t ) « 2e - st0 + 3
(10) (t - 1)U (t - 1) 根据复频域微分特性： (-t ) n f (t ) « F ( n ) ( s ) 1 1 -tU (t ) « ( ) ' = - 2 s s 1 \tU (t ) « 2 s 根据时移特性： e- s (t - 1)U (t - 1) « 2 s
\ cos tU (t ) «

e −sT
=
−sT
2 − 4e 2
+ 2e −sT
Ts 2
（f） x(t) = sin πt[ε (t)− ε (t − π )]
sin π tε (t ) ↔
π s2 + π 2
L[sin
πtε (t
−π
)]
=
L e jπt
− 2
e− jπt j
ε (t
−π
)
∫ ∫ =
1 2j
∞ π
e
jπt e−st dt
4.3 图 4.2 所示的每一个零极点图，确定满足下述情况的收敛域。
（1） f (t) 的傅里叶变换存在
（2） f (t )e 2t 的傅里叶变换存在
（3） f (t) = 0, t > 0
（4） f (t) = 0, t < 5
【知识点窍】主要考察拉普拉斯变换的零极点分布特性。 【逻辑推理】首先由零极点写出拉普拉斯变换式，再利用反变换求取其原信号，即可求取其收
= cosϕ eω0tj + e−ω0tj − sin ϕ eω0tj − e−ω0tj
2
2j
=
cos 2
ϕ
−
sin 2
ϕ j
e
ω0 t j
+
cosϕ 2
+
sin ϕ 2j
e −ω 0tj
F(s) =
L
cosϕ 2
−
sin ϕ 2j
eω0tj
+
cos 2
ϕ
+
sin ϕ 2j
e
−ω0
t
j
ε
(t
)
∫ ∫ =

《信号与系统》第四章习题参考答案4-1 解 （1）111()ataL es s a s s a -⎡⎤-=-=⎣⎦++ （2）[]2221221sin 2cos 111s s L t t s s s ++=+++++ （3）()2212tL te s -⎡⎤=⎣⎦+（4）[]21sin(2)4L t s =+，由S 域平移性质，得 ()21s i n (2)14tL e t s -⎡⎤=⎣⎦++ （5）因为1!nn n L t s +⎡⎤=⎣⎦，所以 []2211212s L t s s s++=+= 由S 域平移性质，得 ()()23121ts L t e s -+⎡⎤+=⎣⎦+（6）()2211cos sL at s s a -=-⎡⎤⎣⎦+，由S 域平移性质，得 (){}()2211cos ts L at e s s aβββ-⎡⎤-=-⎣⎦+++ （7）232222L t t s s ⎡⎤+=+⎣⎦ （8）732()327tL t es δ-⎡⎤-=-⎣⎦+ （9）[]22sinh()L t s βββ=-，由S 域平移性质，得()22sinh()atL e t s a βββ-⎡⎤=⎣⎦+-（10）由于()211cos ()cos 222t t Ω=+Ω 所以 222221111c o s ()22424ss L t s s s s ⎛⎫⎡⎤Ω=+∙=+ ⎪⎣⎦+Ω+Ω⎝⎭（11）()()()11111at t L e e a a s a s s a s βββββ--⎡⎤⎛⎫-=-= ⎪⎢⎥--++++⎣⎦⎝⎭ （12）由于()221cos()1ts L e t s ωω-+⎡⎤=⎣⎦++所以 ()()()221cos()1a t a s e L et s ωω--++⎡⎤=⎣⎦++（13）因为(2)(1)(1)(1)(1)(1)t t t te u t e t e e u t ------⎡⎤-=-+-⎣⎦且()(1)(1)2(1)(1)(1)11sst t e e L t eu t L eu t s s ------⎡⎤⎡⎤--=-=⎣⎦⎣⎦++所以 ()(1)(2)2211(2)(1)(1)11s t s s e L teu t e e s s s -----⎡⎤+⎡⎤-=+=⎢⎥⎣⎦+++⎣⎦（14）()(1)tL e f t F s -⎡⎤=+⎣⎦，由尺度变换性质，得(1)ta t L e f aF as a -⎡⎤⎛⎫=+⎢⎥ ⎪⎝⎭⎣⎦（15）()t L f aF as a ⎡⎤⎛⎫=⎪⎢⎥⎝⎭⎣⎦，再由s 域平移性质，得 []2()()at t L e f aF a s a aF as a a -⎡⎤⎛⎫=+=+ ⎪⎢⎥⎝⎭⎣⎦（16）31cos(6)cos (3)cos(3)2t t t -=∙13cos(9)cos(3)44t t =+32213cos (3)48149s s L t s s ⎡⎤=+⎣⎦++由s 域微分性质，得()()22322222213181327cos (3)481494819d s s s s L t t ds s s s s ⎡⎤--⎛⎫⎢⎥⎡⎤=-+=+ ⎪⎣⎦⎢⎥++⎝⎭++⎣⎦（17）[]2cos(2)4sL t s =+，连续两次应用s 域微分性质，有 []()2224cos(2)4s L t t s-=+，()3232224cos(2)4s sL t t s-⎡⎤=⎣⎦+（18）111atL es s a -⎡⎤-=-⎣⎦+，由s 域积分性质，得111111(1)at sL e ds t s s a ∞-⎛⎫⎡⎤-=- ⎪⎢⎥+⎣⎦⎝⎭⎰ln()ln ln s s a s s a ⎛⎫=+-=- ⎪+⎝⎭ （19）351135tt L ee s s --⎡⎤-=-⎣⎦++，由s 域积分性质，得 33111115ln 353t t s e e s L ds t s s s --∞⎛⎫⎡⎤-+⎛⎫=-= ⎪ ⎪⎢⎥+++⎝⎭⎣⎦⎝⎭⎰（20）()22sin aL at s a =⎡⎤⎣⎦+，由s 域积分性质，得()1122211sin 1arctan 21s s at s a s L ds d t s a a a s a π∞∞⎡⎤⎛⎫⎛⎫===-⎢⎥ ⎪ ⎪+⎝⎭⎝⎭⎛⎫⎣⎦+ ⎪⎝⎭⎰⎰ 4-2 解（1）因为()()sin ()2T f t t u t u t ω⎡⎤⎛⎫=--⎪⎢⎥⎝⎭⎣⎦()sin ()sin 22T T t u t t u t ωω⎡⎤⎛⎫⎛⎫=+-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 所以可借助延时定理，得()()sin ()sin 22T T L f t L t u t L t u t ωω⎧⎫⎡⎤⎛⎫⎛⎫=+--⎡⎤⎡⎤⎨⎬ ⎪ ⎪⎢⎥⎣⎦⎣⎦⎝⎭⎝⎭⎣⎦⎩⎭222222221sT T s ee S S S ωωωωωω--⎛⎫=+=+ ⎪+++⎝⎭（2）因为()()()sin sin cos cos sin t t t ωϕωϕωϕ+=+ 所以()222222cos sin cos sin sin s s L t s s s ωϕϕωϕϕωϕωωω++=+=⎡⎤⎣⎦+++ 4-3 解此题可巧妙运用延时性质。

信号与系统（西安工程大学）知到章节测试答案智慧树2023年最新第一章测试1.周期信号，其周期为（）参考答案:82.=( )参考答案:13.积分的值为（）。

参考答案:24.已知，则等于（）。

参考答案:5.已知某语音信号，对其进行运算得到信号，与信号相比，信号将发生什么变化( )参考答案:长度变长、音调变低第二章测试1.系统的零输入响应是指仅由系统的激励引起的响应。

（）参考答案:错2.系统的零输入响应表达形式一定与其微分方程的通解形式相同，系统的零状态响应表达形式一定与其微分方程的特解形式相同。

（）参考答案:错3.卷积的方法只适用于线性时不变系统的分析（）。

参考答案:对4.单选题：单位阶跃信号作用于某线性时不变系统时，零状态响应为，则此系统单位冲激响应为（）参考答案:5.判断题：两个线性时不变系统级联，其总的输入输出关系与它们在级联中的次序没有关系。

（）参考答案:对第三章测试1.连续非周期信号频谱的特点是( )。

参考答案:连续;非周期2.若对进行理想取样，其奈奎斯特取样频率为，对进行取样，其奈奎斯特取样频率为 ( )。

参考答案:3.如图所示信号，其傅里叶变换=F []，等于（）。

参考答案:24.如图：所示周期信号，该信号不可能含有的频率分量是（）。

参考答案:1 Hz5.已知信号的频谱的最高角频率为，的频谱的最高角频率为，信号的最高角频率等于( )。

参考答案:第四章测试1.请判断下面说法是否正确：若连续时间信号是有限时宽信号，且绝对可积，则其拉氏变换的收敛域为整个s平面。

( )参考答案:对2.利用常用函数的象函数及拉普拉斯变换的性质，函数的拉普拉斯变换为（）。

参考答案:3.描述某LTI系统的微分方程为，则激励下的零状态响应为（）。

参考答案:4.如图所示的复合系统，由四个子系统组成，若各个子系统的系统函数或冲激响应分别为：则复合系统的冲激响应为（）。

参考答案:5.描述某连续线性时不变系统的微分方程为，系统的冲激响应为（），阶跃响应为（）。

第5-10页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.1 拉普拉斯变换
四、常见函数的单边拉普拉斯变换
1. (t ) 1, 2.( t) 或1 3. ( t ) s, 4. 指数信号e
1
s
, 0

1 s s0
s0t
(t 2)
f1(t) 1 0 1 f2(t) 1 t
例1：e (t 2) e
-t
2
e
(t 2)
e
2

1 s 1
e
2s
-1 0
第5-17页
■
1
t
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.2 拉普拉斯变换性质
1 1e sT
例2： 单边冲激 T(t ) 1 e sT e s 2T 例3： 单边周期信号 fT(t ) (t ) f1(t ) f1(t T ) f1(t 2T ) F1(s )(1 e sT e s 2T )
8 e 2 s
s
f(t ) 1 0 1 y(t ) 2 4 t
二、尺度变换
2s
2
(1 e 2 s 2s e 2 s )
2 e 2 s 2 (1 e 2 s 2s e 2 s ) s
第5-16页
■
0
2
4
t
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
拉氏逆变换的物理意义
f (t )
2 j 1

j
j
F (s)est ds

例4-1求下列函数的拉氏变换拉氏变换有单边和双边拉氏变换,为了区别起见,本书以 表示 单边拉氏变换,以 表示 双边拉氏变换.若文字中未作说明,则 指单边拉氏变换.单边拉氏变换只研究 的时间函数,因此,它和傅里叶变换 之间有一些差异,例如在时移定理,微分定理和初值定理等方面.本例只讨论时移 定理.请注意本例各函数间的差异和时移定理的正确应用。

例4-2求三角脉冲函数 如图4-2（a ）所示的象函数和傅里叶变换类似，求拉氏变换的时，往往要借助基本信号的拉氏变换和拉氏变换的性质，这比按拉氏变换的定义式积分简单，为比较起见，本例用多种方法求解。

方法一：按定义式求解方法二：利用线性叠加和时移性质求解方法三：利用微分性质求解 方法四：利用卷积性质求解方法一：按定义式求解()()1-=t tu t f ()s F ()t f ()s F B ()t f 0≥t ()()[]()()()[]ses s t u t u t L t tu L s F -⎪⎭⎫ ⎝⎛+=-+--=-=1111112()t f ()⎪⎩⎪⎨⎧<<-<<=其它 02t 1 21t 0t t t f ()()()()222222221101010102101112221112112sss s s s s st st st st st st ste se s e s e s e s s e s e s dtte dt e dt e s e s t dt e t dt te dt e t f s F -------------∞--=-++-+--=-++⎪⎭⎫ ⎝⎛-=-+==⎰⎰⎰⎰⎰⎰-----方法二：利用线性叠加和时移性质求解由于于是方法三：利用微分性质求解信号的波形仅由直线组成，信号导数的象函数容易求得，或者信号经过几次微分后出现原信号，这时利用微分性质比较简单。

将 微分两次，所得波形如图4-2（b ）所示显然根据微分性质由图4-2（b ）可以看出于是方法四：利用卷积性质求解 可看作是图4-2(c ）所示的矩形脉冲 自身的卷积 于是，根据卷积性质 而所以()()()()()()22112--+---=t u t t u t t tu t f ()[]()[]()0021st e s F t t f L st tu L -=-=()()()222211211s s s ese e s s F ----=+-=()tf 2()()()()[]()2221212s e t t t L dt t f d L --=-+--=⎥⎦⎤⎢⎣⎡δδδ()()()()---'-=⎥⎦⎤⎢⎣⎡00222sf f s F s dt t f d L (),00=-f ()00='-f ()()221s e s F s --=()()2211se s s F --=()()()tf t f t f 11*=()t f ()t f 1()()()s F s F s F 11=()()ses s F --=111()()2211s e s s F --=例4-3应用微分性质求图4-3（a ）中的 象函数下面说明应用微分性质应注意的问题，图4-3（b ）是 的导数的波形。

j n e 3

j n
e3


1 n
sin

n 3

,
n

0, 1,
2,
2
《信号与系统》教与学第四章答案
4.4 周期信号 f (t ) 的双边频谱 Fn 如图所示，求其三角函数表达式。
【知识要点：】本题主要考查周期信号的频谱概念，单边谱与双边谱的关系。
（3）计算信号的功率。
【知识要点：】本题主要考查周期信号的频谱概念应用；帕斯瓦尔功率等式应用。
T

2
；
f
t

A0 2

n1
An
cos
nt n

；P
Fn 2 。
n
【解题方法：】利用已知条件观察求出 ，并带入公式计算求出各次谐波分量；
根据单边幅度谱和双边幅度谱的关系、单边相位谱和双边相位谱的关系画出双
边幅度谱和相位谱；最后利用帕斯瓦尔功率等式计算信号的功率。
解：（1）

x

t


16 cos

20
t

4


6
cos

30
t

6


4
cos

40
t

3

10 (rad/s) ，
T

2

2 10

1 (s) ， 5
周期信号所含谐波次数为二次，三次，四次；
求得。
（1） cos( t ) sin 2t
解： T1

4.14
利用能量等式
f
2 (t )dt
1 2
2
F ( j) d ，计算
sin t
2t
2
dt
。
【解题方法：】先利用门函数常用对和对称性求出 sin(2t) 的傅里叶变换， t
4.11 如下图所示信号， f1 (t ) 的傅立叶变换 F1 ( j ) 已知，求信号 f 2 (t ) 的傅立叶 变换 F2 ( j ) 。
解：
f2 (t ) f1 (t t0 ) f1(t t0 ) f1(t ) F1( j)
f1(t t0 ) F1( j)e jt0
9
《信号与系统》教与学第四章答案
解： T1
2
2(s )
T2
2 2
(s)
故该信号为非周期信号。
（2）
cos(
t)
sin(
t)
2
4
T1 T2
2
为无理数，
解： cos
2
t
,
2
4
(s)，
sin
4
t
,
2
8
(s)，
2
4
8 (s)。
4.2 利用奇偶性判断下图所示各周期信号的傅里叶级数中所含的频率量。
【解题方法：】首先根据函数的奇偶特性判断信号的傅立叶级数中包含的正、余 弦分量；再根据函数的谐波特性判断信号的傅立叶级数中包含的 奇谐分量、偶谐分量。
df (t) ( j ) F ( j ) dt
jt
df (t) dt
d( j) F(
d
j)
jF
(j)
j
dF ( j ) d
4t
df (t dt

3
E1(s)
∑
1 s
-2 -1
（a）
1 s
2
∑
Y 1( s )
E2(s)
−2 t
Vo ( s ) ； E ( s)
U (t ) ，求零状态响应 vo (t ) ；
（3）若 e(t ) = 10 cos(5t ) ，求正弦稳态响应 voss (t ) 。
0.25F + e(t) -
2:1
1F
2:1
2F +
C1
C2
C3
R
vo(t
-
题图 4-17-1
4-18 题图 4-18-1 所示电路 （1）若初始无储能，信号源为 is (t ) ，为求 i1 (t ) （零状态响应） ，列写转移函数 H ( s ) ，并给 出对应于 is (t ) = 10 cos(2t )U (t ) 的零状态响应 i1 (t ) ； （2）若初始状态以 i1 (0) ， v 2 (0) 表示（都不等于零） ，但
is(t
)
1Ω + 1F
-
1H
i1(t
is (t ) = 0 ，求 i1 (t ) （零输入响应） 。
v 2( t )
1Ω
题图 4-18-1
4-19 求题图 4-19 中电路的电压传输函数，如果要求响应中不出现 强迫响应分量，激励函数应有怎样的模式？
C
R1
+ +
-)
e(t R2
vo(t)
-
题图 4-19
4-11 用拉氏变换分析法，求下列系统的响应。
d 2 r (t ) dr (t ) （1） +3 + 2r (t ) = 0 ， r (0 − ) = 1 ， r ' (0 − ) = 2 2 dt dt

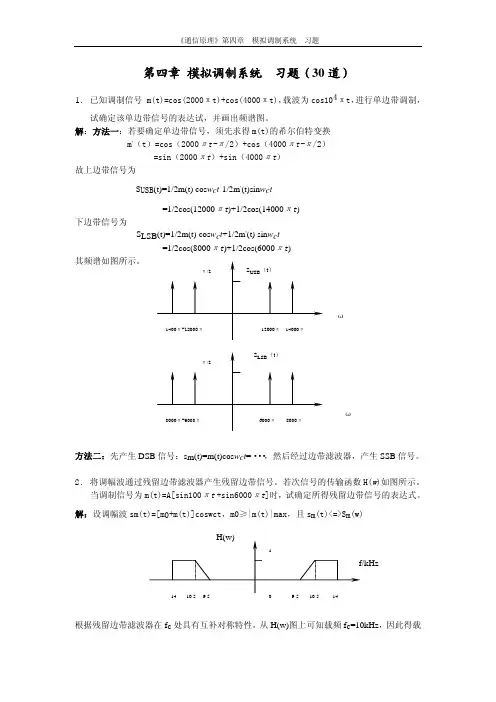
第四章 模拟调制系统 习题（30道）1. 已知调制信号 m(t)=cos(2000πt)+cos(4000πt)，载波为cos104πt，进行单边带调制，试确定该单边带信号的表达试，并画出频谱图。

解：方法一：若要确定单边带信号，须先求得m(t)的希尔伯特变换 m ’（t）=cos（2000πt-π/2）+cos（4000πt-π/2） =sin（2000πt ）+sin（4000πt ） 故上边带信号为S USB (t)=1/2m(t) cos w c t -1/2m ’(t)sin w c t =1/2cos(12000πt )+1/2cos(14000πt ) 下边带信号为S LSB (t)=1/2m(t) cos w c t +1/2m ’(t) sin w c t=1/2cos(8000πt )+1/2cos(6000πt ) 其频谱如图所示。

方法二：先产生DSB 信号：s m (t)=m(t)cos w c t =···，然后经过边带滤波器，产生SSB 信号。

2. 将调幅波通过残留边带滤波器产生残留边带信号。

若次信号的传输函数H(w )如图所示。

当调制信号为m(t)=A[sin100πt +sin6000πt ]时，试确定所得残留边带信号的表达式。

解：设调幅波sm(t)=[m 0+m(t)]coswct，m0≥|m(t)|max，且s m (t)<=>S m (w)根据残留边带滤波器在f c 处具有互补对称特性，从H(w)图上可知载频f c =10kHz ，因此得载波cos20000πt。

故有sm(t)=[m0+m(t)]cos20000πt=m0cos20000πt+A[sin100πt+sin6000πt]cos20000πt=m0cos20000πt+A/2[sin(20100πt)-sin(19900πt)+sin(26000πt)-sin(14000πt)Sm(w)=πm0[σ(w+20000π)+σ(W-20000π)]+jπA/2[σ(w+20100π)-σ(w+19900π)+σ(w-19900π)+σ(w+26000π)-σ(w-26000π)-σ(w+14000π)+σ(w-14000π)残留边带信号为F(t)，且f(t)<=>F(w)，则F(w)=Sm(w)H(w)故有：F(w)=π/2m0[σ(w+20000π)+σ(w-20000π)]+jπA/2[0.55σ(w+20100π)-0.55σ(w-20100π)-0.45σ(w+19900π)+ 0.45σ(w-19900π)+σ(w+26000π) -σ(w-26000π)f(t)=1/2m0cos20000πt+A/2[0.55sin20100πt-0.45sin19900πt+sin26000πt]3.设某信道具有均匀的双边噪声功率谱密度Pn(f)=0.5*10-3W/Hz，在该信道中传输抑制载波的双边带信号，并设调制信号m(t)的频带限制在5kHz，而载波为100kHz，已调信号的功率为10kW.若接收机的输入信号在加至解调器之前，先经过一理想带通滤波器滤波，试问：1.）该理想带通滤波器应具有怎样的传输特性H(w)?2.）解调器输入端的信噪功率比为多少?3.）解调器输出端的信噪功率比为多少?4.）求出解调器输出端的噪声功率谱密度，并用图型表示出来。

题图 4-3-1 解：
11
第四章 傅立叶分析
第 4 章 习题参考答案
4-3-7
1）x(t)是实周期信号，且周期为 6； 3）x(t) = −x(t − 3)
1 3
设某信号x(t)满足下述条件：
2）x(t)的傅里叶系数为ak ，且当k = 0 和 k > 2时，有ak = 0；
1
4） ∫−3 |x(t)|2dt = 6 2 5）a1是正实数。
第四章 傅立叶分析
第 4 章 习题参考答案
第 4 章 习题参考答案
4-1 思考题 答案暂略 4-1 练习题 4-2-2 已知三个离散时间序列分别为 x1 ( n) = cos
2πn 2πn , x3 (n) = e , x 2 (n) = sin 25 10
π x (t ) = sin 4π t + cos 6π t + 时，试求系统输出 y (t ) 的傅立叶级数。 4
解：
3
第四章 傅立叶分析
第 4 章 习题参考答案
4因果系统： y(t) + 4y(t) = x(t)
式中x(t) 为系统输入，y(t)是系统输出。在下面两种输入条件下，求输出y(t)的傅里叶级数 展开： 1）x(t) = cos2πt ；
2
2
= 3 ） f ( t ) Sa (100t ) + Sa
解：
( 60t ) 4）
sin(4π t ) , −∞ < t < ∞ πt
9
第四章 傅立叶分析
第 4 章 习题参考答案
4）T=1/4 4-2-27 设 x(t ) 是一实值信号，在采样频率 ω s = 10000π 时， x(t ) 可用其样本值唯一确定

8 T /2 Asin( 2t / T0 )dt T 0 4A / k , k 1,3,5, x2 (t) A,0 t T / 4
ቤተ መጻሕፍቲ ባይዱ
则 x2 (t)
频谱：
4A

2k 1sin(2k 1) t ,
k 1 0

1
0 10
X ( ) F {sin t ( 1 / 3 ) sin 3 t } 1
X ( ) F { x ( t ) x ( t ) cos 20 t } 6 1 1
X ( ) X ( ) ( 20 ) ( 20 ) / 2 1 1
X ( ) X ( 20 ) / 2 X ( 20 ) / 2 1 1 1
信号与系统第二版曾禹村著北京理工大学出版社第四章作业参考答案由会员分享可在线阅读更多相关信号与系统第二版曾禹村著北京理工大学出版62.
4.2在全波整流电路中，如输入交流电压x(t)，则输出电压y(t)=|x(t)|. (a)当 x(t)=cost,概略地画出输出y(t)的波形并求傅里叶系数。 (b)输入信号中直流分量振幅为多少，输出信号中直流分量振幅为多少？ 解 : (a) y(t)=| cost |，T=π ,ω =2π /T=2. 1 … 0
9
-9Ω -7Ω -13Ω -11Ω 0
2 Aj /
7 Ω 9Ω
11Ω 13Ω
2 Aj 3
31Ω 33Ω 27Ω 29Ω ω
2 Aj 3
…
2 Aj /
2 Aj 9
1 H1(ω )
-15Ω -5Ω 0 5Ω 15Ω ω
X ( 10 ) 1

绪论单元测试1【判断题】(1分)信号到的运算中，若a>1，则信号的时间尺度缩小a倍，其结果是将信号的波形沿时间轴放大a倍。

A.错B.对第一章测试1【判断题】(1分)信号到的运算中，若a>1，则信号的时间尺度缩小a倍，其结果是将信号的波形沿时间轴放大a倍。

A.对B.错2【判断题】(1分)如果某连续时间系统同时满足叠加性和齐次性，则称该系统为线性系统。

A.错B.对3【判断题】(1分)直流信号与周期信号都是功率信号。

A.错B.对4【单选题】(1分)将信号变换为（）称为对信号的平移或移位。

A.B.C.D.5【单选题】(1分)下列各表达式正确的是（）。

A.B.C.D.6【单选题】(1分)积分的结果为（）。

A.3B.C.1D.97【单选题】(1分)设输入为、时系统产生的响应分别为、，并设、为任意实常数，若系统具有如下性质：，则系统为（）。

A.时不变系统B.因果系统C.非线性系统D.线性系统8【单选题】(1分)（）。

A.B.C.D.9【单选题】(1分)，该序列是（）。

A.非周期序列B.周期C.周期D.周期10【多选题】(1分)连续时间系统系统结构中常用的基本运算有（）。

A.微分器B.标量乘法器C.积分器D.加法器11【多选题】(1分)下列等式成立的是（）。

A.B.C.D.12【判断题】(1分)一系统，该系统是线性系统。

()A.错B.对第二章测试1【判断题】(1分)强迫响应是零状态响应与部分自由响应之差。

（）A.对B.错2【判断题】(1分)连续时间系统的单位阶跃响应是系统在单位阶跃信号作用下的响应。

（）A.对B.错3【判断题】(1分)零状态响应是由激励引起的响应。

（）A.错B.对4【判断题】(1分)某连续时间系统是二阶的，则其方框图中需要两个积分器。

（）A.错B.对5【单选题】(1分)若系统的输入信号为，冲激响应为，则系统的零状态响应是()。

A.B.C.D.6【单选题】(1分)卷积的结果是()。

A.B.C.D.7【单选题】(1分)卷积积分等于（）。

第0-6页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案 十五、如图之系统，已知
f (t )
n j nt e
，=1 ; s(t)=cos(t)，
子系统的冲激响应h1(t)=e–|t| ， 频率响应 1, 1.5 rad/s
H ( j ) 0,
信号与系统 电子教案
第四章习题
一、求下列信号的傅里叶变换：
（1）f1 (t ) e
3(t 1)
(t 1)
(jω+3)e–jω
（2） f 2 (t ) (t 2 9)
（3） f 3 (t ) e sgn(3 2t )
jt
2πδ(ω) – 6Sa(3ω)
j 2 j 2 ( 1) e 1
2H iS(t) uS(t) 1Ω i(t) 1F
第0-9页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
第0-10页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
第0-11页
■
©西安电子科技大学电路与系统教研中心
第0-2页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案 七、函数 f1 (t )
1 t 2 2t 2
,求F(jω)。
八、求图中所示信号的傅里叶变换F(jω)。
f(t) 2 1 -4 -2 0 2 4 t
2 F(jω )
九、已知F(jω)的图形如图所示， 求原函数f(t)。
第0-3页
■
0
1
ω
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案

信号与系统（段哲民)第三版第四章答案全解4.1 选择题答案解析(C)伯努利信号是一个具有有限时间持续性的信号，因此是非因果信号。

解析：伯努利信号只在有限时间内存在，而非因果信号是只存在于负时间的信号。

(D)和三角函数的区别是，余弦函数的相位是0，而不是1。

解析：和三角函数不同，余弦函数的相位是0，表示相位没有滞后。

(B)碰撞行为是随机过程，因此其幅度表示为随机变量是正确的。

解析：碰撞行为是随机过程，其幅度表示为随机变量。

4.2 填空题答案解析1.以下哪个信号不是周期信号？(B)解析：周期信号是指在时间轴上具有循环性质的信号。

正方脉冲信号和方波信号都是周期信号，而冲击信号不是周期信号。

2.正弦信号频率是50Hz，则周期为______。

解析：频率和周期的关系为$f=\\frac{1}{T}$。

根据公式可知，周期$T=\\frac{1}{f}=0.02s$。

3.已知信号$y(t)=3\\sin(2\\pi t + \\frac{\\pi}{6})$，则相位为______。

解析：相位指信号相对于某参考信号的滞后程度。

对于正弦信号，相位为$\\theta = 2\\pi t + \\frac{\\pi}{6}$4.3 解答题答案解析1.请证明复指数函数$e^{j\\theta}$是周期信号。

解析：复指数函数$e^{j\\theta}$可以表示为$e^{j(\\omega_0t+\\phi)}=e^{j\\omega_0t}e^{j\\phi}$，其中$\\omega_0$为角频率。

由于$|\\phi| < \\pi$，所以$e^{j\\phi}$是一个衰减的振荡函数，它是一个周期信号。

2.指出以下信号的类型：(1)冲击信号 (2)阶跃信号 (3)斜坡信号解析：(1) 冲击信号是一个非周期信号；(2) 阶跃信号是一个非周期信号；(3) 斜坡信号是一个非周期信号。

3.已知信号y[y]=2y[y−y]，请将该信号分解为若干复指数信号的叠加形式。

【最新整理，下载后即可编辑】 第四章习题 4.6 求下列周期信号的基波角频率Ω和周期T 。

（1）t j e 100 （2）)]3(2cos[-t π （3）)4sin()2cos(t t + （4）)5cos()3cos()2cos(t t t πππ++（5）)4sin()2cos(t t ππ+ （6）)5cos()3cos()2cos(t t t πππ++ 4.7 用直接计算傅里叶系数的方法，求图4-15所示周期函数的傅里叶系数（三角形式或指数形式）。

图4-154.10 利用奇偶性判断图4-18示各周期信号的傅里叶系数中所含有的频率分量。

图4-184-11 某1Ω电阻两端的电压)(t u 如图4-19所示，（1）求)(t u 的三角形式傅里叶系数。

（2）利用（1）的结果和1)21(=u ，求下列无穷级数之和 ......7151311+-+-=S （3）求1Ω电阻上的平均功率和电压有效值。

（4）利用（3）的结果求下列无穷级数之和 (7)151311222++++=S图4-194.17 根据傅里叶变换对称性求下列函数的傅里叶变换（1）∞<<-∞--=t t t t f ,)2()]2(2sin[)(ππ（2）∞<<-∞+=t t t f ,2)(22αα （3）∞<<-∞⎥⎦⎤⎢⎣⎡=t t t t f ,2)2sin()(2ππ4.18 求下列信号的傅里叶变换（1）)2()(-=-t e t f jt δ （2）)1(')()1(3-=--t e t f t δ（3）)9sgn()(2-=t t f （4）)1()(2+=-t e t f t ε（5）)12()(-=tt f ε4.19 试用时域微积分性质，求图4-23示信号的频谱。

图4-234.20 若已知)(j ])([ωF t f F =，试求下列函数的频谱：（1）)2(t tf （3）dt t df t )( （5）)-1(t)-(1t f （8）)2-3(t f e jt （9）tdt t df π1*)(4.21 求下列函数的傅里叶变换（1）⎩⎨⎧><=0,1,)(jωωωωωF（3）)(3cos2)(jωω=F（5）ωωωω1)(2n-2sin2)(j+=∑=jneF4.23 试用下列方式求图4-25示信号的频谱函数（1）利用延时和线性性质（门函数的频谱可利用已知结果）。

1 3
s +1 ) ，复频移性质、尺度变换、S 域微分 3
b
b ⎤ 1 s - s ⎡ (4) f (at − b) = f ⎢a(t − )⎥ ↔ F( )e a ，时移性质、尺度变换 a ⎦ a a ⎣
4．7 题图 4．2 所示为从 t=0 起始的周期信号。求 f(t)的单边拉氏变换。
解： (a) f (t ) = f a (t ) *
∑ δ (t − nT )
n =0
∞
- s 1 f a (t ) = ε (t ) − ε (t − T / 2) ↔ (1 - e 2 ) s - s 1 1 1- e 2 1 = = ∴ F(s) = (1 - e 2 ) T -s ⎞ s 1 - e -sT s 1 - e -sT ⎛ ⎜ s ⎜1 + e 2 ⎟ ⎟ ⎝ ⎠ T T - s
2
K1 =
2 jπ / 6 2 − jπ / 6 e , K2 = e 3 3
∴ h(t ) =
π 4 −t 2 −t e cos( 3t + )ε (t ) = e 6 3 3
2
(
3cos 3t - sin 3t ε (t )
)
当 u s (t ) = ε (t ) 时， U( s ) = H ( s) =
−2 t 解：(1) e f (2t ) ↔
1 s+2 F( ) ，复频移性质、尺度变换 2 2 ⎡1 ⎤
2 2 -2s (2) (t − 2) f ( t − 1) = (t − 2) f ⎢ (t − 2)⎥ ↔ 2F′′(2s)e ，时移性质、尺度变换、S 域微分 2 ⎣2 ⎦
1
−t (3) te f (3t ) ↔ − F′(