第四章:空间力系
- 格式:doc
- 大小:564.50 KB
- 文档页数:9




第四章空间力系一、要求1、能熟练地计算力在空间直角坐标轴上的投影和力对轴之矩。
2、对空间力偶的性质及其作用效应要有清晰的理解。
3、了解空间力系向一点简化的方法和结果。
4、能应用平衡条件求解空间汇交力系、空间任意力系、空间平行力系的平衡问题。
5、能正确地画出各种常见空间约束的约束反力。
二、重点、难点1、本章重点:力在空间直角坐标轴上的投影和力对轴之矩。
空间汇交力系、空间任意力系、空间平行力系的平衡方程的应用。
各种常见的空间约束及约束反力。
2、本章难点:空间矢量的运算,空间结构的几何关系与立体图。
三、学习指导1、空间力系的基本问题及其研究方法空间力系研究的基本问题仍然是静力学的三个基本问题,即:物体的受力分析、力系的等效替换和力系的平衡条件。
空间力系是力系中最普遍的情形,其它各种力系都是它的特殊情形。
按由浅入深、由特殊到一般的认识规律研究空间力系,是从理论上对静力学作一个系统而完整的总结。
与平面力系的研究方法相似,这里也采用力向一点平移的方法将空间任意力系分解为空间汇交力系和空间力偶系,再应用这两个力系的合成方法来简化原力系,然后根据简化结果推导出平衡条件。
由于空间力系各力作用线分布在空间,因而使问题复杂化。
出现了力在坐标轴上的二次投影法、力对轴的矩以及用向量表示力对点的矩和力偶矩等新问题,简化的结果和平衡方程也复杂了。
2、各类力系的平衡方程各类力系的独立的平衡方程的数目不变。
但是平衡方程的形式可以改变。
上表列出的是一般用形式。
解题指导1、对于解力在直角坐标轴上投影或力沿直角坐标轴分解这类问题,重要的是确定力在空间的位置。
一般解题的思路如下:(1)认清题意,仔细查看结构(或机构)的立体图,它由哪些部件组成,各部件在空间的位置,以及它们和坐标轴的关系。
(2)认清力的作用线在结构(或机构)的哪个平面内,寻找它与坐标面的交角,然后找力与坐标平面的夹角及力与坐标轴的夹角。
(3)考虑用一次投影或二次投影的方法求解。


·36·第4章 空间力系一、是非题(正确的在括号内打“√”、错误的打“×”)1.力在坐标轴上的投影是代数量,而在坐标面上的投影为矢量。
( √ )2.力对轴之矩是力使刚体绕轴转动效应的度量,它等于力在垂直于该轴的平面上的分力对轴与平面的交点之矩。
( √ )3.在平面问题中,力对点之矩为代数量;在空间问题中,力对点之矩也是代数量。
( × )4.合力对任一轴之矩,等于各分力对同一轴之矩的代数和。
( √ )5.空间任意力系平衡的必要与充分条件是力系的主矢和对任一点的主矩都等于零。
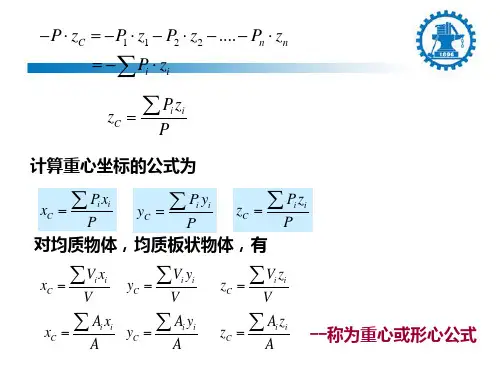
( √ ) 6.物体重力的合力所通过的点称为重心,物体几何形状的中心称为形心,重心与形心一定重合。
( × ) 7.计算一物体的重心,选择不同的坐标系,计算结果不同,因而说明物体的重心位置是变化的。
( × ) 8.物体的重心一定在物体上。
( × )二、填空题1.空间汇交力系共有三个独立的平衡方程,它们分别表示为0=∑xF、0=∑yF和0=∑zF 。
空间力偶系共有三个独立的平衡方程,它们分别表示为0=∑xM、0=∑yM和0=∑zM。
而空间任意力系共有六个独立的平衡方程,一般可表示为0=∑xF、0=∑yF、0=∑zF 、0)(=∑F xM 、 0)(=∑F yM 和0)(=∑F zM 。
2.由n 个力组成的空间平衡力系,如果其中的(n -1)个力相交于A 点,那么另一个力也必定通过点A 。
3.作用在同一刚体上的两个空间力偶彼此等效的条件是力偶矩矢相等。
4.空间力对一点的矩是一个矢量,而空间力对某轴的矩是一个代数量。
5.空间力F 对任一点O 之矩)(F M O 可用矢量积来表示,即F r F M ⨯=)(O 。
写成解析表达式为k j i F M )()()()(x y z x y z O yF xF xF zF zF yF -+-+-=。
6.当空间力与轴相交时,力对该轴的矩等于零。

第四章 空间力系4-1 力系中,F 1=100 N 、F 2=300 N 、F 3=200 N ,各力作用线的位置如图所示。
试将力系向原点O 简化。
解:由题意得 N 34552200132300R -=⋅-⋅-=x FN 250133300R =⋅=y F N 6.1051200100R =⋅-=z Fm N 8.513.0512001.0133300⋅-=⋅⋅-⋅⋅-=x Mm N 6.361.013220020.0100⋅-=⋅⋅+⋅-=y Mm N 6.1033.0522002.0133300⋅=⋅⋅+⋅⋅=z M 主矢 N 4262R 2R 2R R =++=x y z F F F F ,N )6.10250345(R k j i ++-=F主矩 m N 122222⋅=++=z y x O M M M M ,m N )1046.368.51(⋅+--=k j i O M4-3 图示力系的三力分别为N 3501=F 、N 4002=F 和N 6003=F ,其作用线的位置如图所示。
试将此力系向原点O 简化。
解:由题意得N 144216001810060350'R -=⋅-⋅=x F N1010866.0600707.04001810080350'R =⋅+⋅+⋅=y FN 517707.04001810090350'R -=⋅--⋅=z F主矢 N 11442'R 2'R 2'R R =++=z y x F F F 'F , N )5171011144(R k j i F -+-='; m N 48mm N 48000120707.0400601810090350⋅-=⋅-=⋅⋅-⋅⋅-=x M m N 07.21mm N 21070901810090350⋅=⋅=⋅⋅=y M 602160090866.0600601810060350901810080350⋅⋅+⋅⋅-⋅⋅-⋅⋅=z M m N 4.19mm N 19400⋅-=⋅-=主矩 m N 55.9mm N 55900222⋅=⋅=++=z y x O M M M Mm N )4.191.2148(⋅-+-=k j i M O4-5 轴AB 与铅直线成α角,悬臂CD 与轴垂直地固定在轴上,其长为a ,并与铅直面zAB 成θ角,如图所示。



第四章空间力系本章将研究空间力系的简化和平衡条件。
工程中常见物体所受各力的作用线并不都在同一平面内,而是空司分布的,例如车床主轴、起重设备、高压输电线塔和飞机的起落架等结构。
设计这些结构时,需用空间力系的平衡条件进行计算。
与平面力系一样,空间力系可以分为空间汇交力系、空司力偶系和空间任意力系来研究。
§4-1 空间汇交力系1.力在直角坐标轴上的投影和力沿直角坐标轴的分解若已知力F与正交坐标系Oxyz三轴间的夹角分别为α、β、γ,如图4-1所示,则力在三个轴上的投影等于力F的大小乘以与各轴夹角的余弦,即X=cosαY=cosβ (4-1)Z=cosγ当力与坐标轴Ox、Oy间的夹角不易确定时,可把力先投影到坐标平面Oxy上,得到力,然后再把这个力投影到x、y轴上。
在图4-2中,已知角γ和,则力在三个坐标轴上的投影分别为X=sinγcosY=sinγsin (4-2)Z=cosγ若以、、表示力F沿直角坐标轴x、y、z的正交分量,以i、j、k分别表示沿x、y、z坐标轴方向的单位矢量,如图4-3所示,则图4-2=++=X i+Y j+Z k (4-3)由此,力在坐标轴上的投影和力沿坐标轴的正交分矢量间的关系可表示为:=X i,=Y j,=Z k (4-4)如果己知力F在正交轴系Oxyz的三个投影,则力F的大小和方向余弦为=cos(,i)=cos(,j)= (4-5)cos(,k)=例4-1图4-4所示的圆柱斜齿轮,其上受啮合力的作用。
已知斜齿轮的齿倾角(螺旋角) β和压力角α,试求力沿x、y和z轴的分力。
解:先将力向z轴和Oxy平面投影,得Z=-sinα=cosα再将力向x、y轴投影,得X=-sinβ=-cosαsinβY=-cosβ=-cosαcosβ则沿各轴的分力为=-cosαsinβi,=-cosαcosβj,=-sinαk式中i、j、k为沿x、y、z轴的单位矢量,负号表明各分力与轴的正向相反。
静力学第四章空间力系杨文刚车床主轴受力分析§4-1 空间汇交力系§4-2 力对点之矩和力对轴之矩§4-3 空间力偶系§4-4 空间任意力系§4-5 重心空间汇交力系空间力偶系空间任意力系空间力系主要内容学习方法:在平面力系的基础上推广;注意其与平面力系的异同。
1 回顾平面汇交力系:力的平行四边形法则∑=iR F F 简化结果:平衡条件:=∑i F ∑=0x F ∑=0y F平面汇交力系合成的平行四边形法则对空间汇交力系是否适用?∑=i R F F 简化结果:平衡条件:=∑i F ∑=0x F ∑=0y F ∑=0zF2 空间汇交力系的简化与平衡条件§4-2 力对点之矩和力对轴之矩1 回顾平面力对点之矩1.大小:力F 与力臂的乘积2.方向:转动方向两个要素:()hF F M±=注意:其力矩作用面固定。
代数量2 空间力对点之矩三要素:(1)大小:力F与力臂的乘积(2)方向:转动方向(3)作用面:力矩作用面。
定位矢量2 空间力对点之矩3 力对轴之矩力与轴相交或与轴平行时(力与轴在同一平面内时),力对该轴的矩为零。
代数量3 力对轴之矩= -+ 0=1 回顾平面力偶in i i M MM ∑==∑=1两个要素:a.大小:力与力偶臂乘积b.方向:转动方向力偶矩d F M ⋅±=代数量=∑i M 简化结果:平衡条件:2 空间力偶空间力偶的三要素:(1)大小:力与力偶臂的乘积;(2)方向:转动方向;(3)作用面:力偶作用面。
2 空间力偶力偶矩矢矢量力偶矩相等的力偶等效2 空间力偶(1)力偶中两力在任意坐标轴上投影的代数和为零。
(2)力偶对任意点取矩都等于力偶矩,不因矩心的改变而改变。
(3)只要保持力偶矩不变,力偶可在其作用面内任意移转,且可以同时改变力偶中力的大小与力偶臂的长短,对刚体的作用效果不变。
(5)只要保持力偶矩不变,力偶可从其所在平面移至另一与此平面平行的任一平面,对刚体的作用效果不变。
第四章空间力系一、要求1、能熟练地计算力在空间直角坐标轴上的投影和力对轴之矩。
2、对空间力偶的性质及其作用效应要有清晰的理解。
3、了解空间力系向一点简化的方法和结果。
4、能应用平衡条件求解空间汇交力系、空间任意力系、空间平行力系的平衡问题。
5、能正确地画出各种常见空间约束的约束反力。
二、重点、难点本章重点:力在空间直角坐标轴上的投影和力对轴之矩。
空间汇交力系、空间任意力系、空间平行力系的平衡方程的应用。
各种常见的空间约束及约束反力。
b5E2RGbCAP2、本章难点:空间矢量的运算,空间结构的几何关系与立体图。
三、学习指导1、空间力系的基本问题及其研究方法空间力系研究的基本问题仍然是静力学的三个基本问题,即:物体的受力分析、力系的等效替换和力系的平衡条件。
空间力系是力系中最普遍的情形,其它各种力系都是它的特殊情形。
按由浅入深、由特殊到一般的认识规律研究空间力系,是从理论上对静力学作一个系统而完整的总结。
p1EanqFDPw与平面力系的研究方法相似,这里也采用力向一点平移的方法将空间任意力系分解为空间汇交力系和空间力偶系,再应用这两个力系的合成方法来简化原力系,然后根据简化结果推导出平衡条件。
由于空间力系各力作用线分布在空间,因而使问题复杂化。
出现了力在坐标轴上的二次投影法、力对轴的矩以及用向量表示力对点的矩和力偶矩等新问题,简化的结果和平衡方程也复杂了。
DXDiTa9E3d2、各类力系的平衡方程力系类型平衡方程独立的方程的数目空间任意力系6汇交力系3平行力系3力偶系3平面任意力系3汇交力系2平行力系2力偶系1各类力系的独立的平衡方程的数目不变。
但是平衡方程的形式可以改变。
上表列出的是一般用形式。
解题指导对于解力在直角坐标轴上投影或力沿直角坐标轴分解这类问题,重要的是确定力在空间的位置。
一般解题的思路如下:RTCrpUDGiT认清题意,仔细查看结构<或机构)的立体图,它由哪些部件组成,各部件在空间的位置,以及它们和坐标轴的关系。
5PCzVD7HxA认清力的作用线在结构<或机构)的哪个平面内,寻找它与坐标面的交角,然后找力与坐标平面的夹角及力与坐标轴的夹角。
jLBHrnAILg(3)考虑用一次投影或二次投影的方法求解。
2、计算力对轴之矩,一般令矩轴位于一个坐标面内,寻找与矩轴垂直的平面,然后按题意选择以下两种方法:将力投影到垂直于轴的平面上,然后按平面上力对点的矩计算。
怎样将力投影到平面上呢?可先由力的作用点向平面作垂线,再寻找力和垂线所在平面与该平面的交线,然后将力向交线投影。
xHAQX74J0X将力沿直角坐标轴分解,然后根据合力之矩定理计算。
怎样选择分解方向呢?一般让两个分力在与矩轴垂直的平面内,一个分力平行于矩轴。
LDAYtRyKfE3、空间力系的解题技巧有以下两点:平衡力系在任意轴上的投影等于零,在选择三个投影轴时,可不相交,可不相互垂直,但三轴不能共面,任意二轴也不能平行。
如果所选投影轴垂直于未知力或它所在的平面,则可减少平衡方程中未知力的数量,便于求解方程。
Zzz6ZB2Ltk平衡力系对任意轴的力矩都必须等于零,在选择三个力矩轴时,可不相交。
可不相互垂直。
另外,用力矩方程也能保证合力为零,可用力矩方程代替投影方程。
因此,空间力系的平衡方程可以有四矩式、五矩式、六矩式。
如果所选取的矩轴与未知力平行或通过几个未知力<或力的作用线)的交点,则可使平衡方程中的未知力的数量减少,便于求解方程。
dvzfvkwMI1四、典型例题解读例题4. 1 空间平行力系简化的结果是什么?可能合成为力螺旋吗?解答:空间平行力系简化的中间结果仍为一主矢和主矩<主矢与主矩垂直),简化的最后结果可为一合力、合力偶或平衡,唯独不可能是力螺旋。
因主矢与主矩相垂直。
rqyn14ZNXI例题4. 2 <1)空间力系中各力的作用线平行于某一固定平面;<2)空间力系中各力的作用线分别汇交于两个固定点。
试分析这两种力系各有几个平衡方程?EmxvxOtOco解答:<1)空间力系中各力的作用线平行于某一固定平面,取某轴垂直于此固定平面,则各力在此轴的投影均为零,此方程失去使用价值,所以此力系的平衡方程个数等于或小于五个。
<2)空间力系中各力的作用线分别汇交于两个固定点,过这两点做一轴,此力系各力对此轴的力矩均为零,此方程失去求解价值,所以此力系的平衡方程个数等于或小于五个。
SixE2yXPq5例题4. 3 传动轴用两个止推轴承支持,每个轴承有三个未知力,共6个未知量。
而空间任意力系的平衡方程恰好有6个,是否为静定问题?6ewMyirQFL解答:此问题为静不定问题,因为六个轴承约束反力对此轴的力矩均为零,此力系的独立方程为五个。
例题4. 4 空间任意力系向两个不同点简化,试问下述情况是否可能:<1)主矢相等,主矩也相等;<2)主矢不相等,主矩相等;<3)主矢相等,主矩不相等;<4)主矢、主矩都不相等。
kavU42VRUs解答:空间任意力系的主矢与简化中心无关,所以若向不同的点简化,主矢不相等是不可能的,因此<2)、<4)两种情况是不可能的。
空间任意力系的主矩一般与简化中心有关,所以<3)是可能的。
<1)主矢相等、主矩也相等也是可能的<两点均在主矢作用线上)。
y6v3ALoS89例题4. 5 一均质等截面直杆的重心在哪里?若把它弯成半圆形,重心的位置是否改变?解答:在几何形心上<杆长一半处),若把它弯成半圆形,重心的位置改变。
例题4.6 当物体质量分布不均匀时,重心和几何中心还重合吗?为什么?解答:一般不重合。
因为几何中心只与物体的几何形状有关,而物体的重心与物体的质量分布有关,这是两个不同的概念与不同的度量。
M2ub6vSTnP例题4. 7 计算一物体重心的位置时,如果选取的坐标系不同,重心的坐标是否改变?重心在物体内的位置是否改变?0YujCfmUCw解答:同一点在不同的坐标系里,其坐标是不同的,所以,计算物体的重心位置时,如果选取的坐标系不同,重心的坐标要改变。
重心在物体内的位置不会因坐标系的选择不同而改变。
eUts8ZQVRd例题4. 8 已知,,,作用位置及尺寸如下图所示;求力系向点简化的结果。
解:力系主矢在轴上的投影为:1力系对点的主矩在轴上的投影为:力系向点简化所得的力和力偶的各个分量如图所示。
例题4. 9已知小正方格的边长为,各力的大小及作用线位置如图所示;求力系的合力。
解:该平行力系的合力为设合力与平面的交点为,由合力矩定理有:由,解出:,力系的合力如图中所示。
例题4. 10 已知处受力作用,板和杆的自重不计;求各杆的内力。
解:板的受力如图,由、以及,分别得,,再由,,,,得<压),,<压)例题4. 11 下图所示均质矩形板重为,用球铰链和碟形铰链<活页)固定在墙上,并用绳索维持在水平位置。
已知。
试求绳索所受张力及、处的约束力。
sQsAEJkW5T解:分析矩形板的受力。
由于蝶形铰水平放置,可认为它不能限制板沿轴的轴向位移,故;球铰处的约束力。
于是板所受未知力GMsIasNXkA。
为了尽量做到由一个平衡方程求解一个未知力,需要灵活选用平衡方程,特别是力对轴之矩形式的平衡方程:,<1)TIrRGchYzg⑦ P78 例题3-7,,<2),,<3)将式<2)代入式<3),得。
进而有,,< 4),,< 5),,<6)灵活选用平衡方程,往往可以避免求解联立方程。
与考察二维刚体的平衡问题相似,最好采用力对轴之矩形式的平衡方程。
因此,选择哪一根轴便很有考究。
例如,为求可选为取矩轴,于是有7EqZcWLZNX,显然,此式比式<3)简单。
由计算结果可知,。
这样,矩形板就可看成在平面内只受三力作用的系统,这时空间力系化为平面力系。
当然,此三力应汇交于该平面内一点,如图所示。
lzq7IGf02E例题4. 12 已知力偶与,曲杆自重不计;求使曲杆保持平衡的力偶矩和支座、的反力。
解曲杆整体受力如图,由平衡方程,,,,,,解得:,,c ,,例题4. 13 已知等边三角形板的边长为,在板内作用一矩为的力偶,板、杆的自重不计;求各杆的内力。
解:三角形板受力如图,由,,,,,,解得:<压),<拉)例题4. 14 已知均质杆、分别重为与,、、均为球铰,端靠在铅直光滑的墙上,,求求球铰、的约束反力及点墙面的法向反力。
zvpgeqJ1hk解:先研究杆,受力图如图所示,由,,得再取、两杆为一体来研究,受力如图所示,由,,,,,,解得:,,,,,例题 4. 15 已知工字钢截面尺寸如图所示;求此截面的几何中心。
解:,,,由对称性,,而申明:所有资料为本人收集整理,仅限个人学习使用,勿做商业用途。
20m m150m m200m m123。