第四章:空间力系范文
- 格式:doc
- 大小:801.50 KB
- 文档页数:10





空间平行力系
空间平行力系是指在空间内,由若干个平行的力构成的力系。
这些力在大小、方向和
作用点上都是平行的,因此不会互相干扰或叠加,其作用效果可以看成是多个力的简单叠
加而成的。
空间平行力系的重要性在于它广泛存在于自然界和工程实践中,如桥梁、建筑结构、
飞机机身等,这些结构所承受的荷载往往是由若干个平行的力组成的。
了解和应用空间平
行力系的知识和方法,可以帮助我们更好地设计和维护这些结构,从而提高其稳定性和安
全性。
在计算空间平行力系的作用效果时,我们需要考虑以下几个因素:
1. 空间平行力系的矢量表示:将每个力看成一个矢量,并将它们画在同一坐标系中,从而得到一个矢量图。
2. 矢量的合成:对于每个矢量,我们可以将其拆分成一个平行于某个坐标轴的分量
和一个垂直于其它坐标轴的分量。
然后,我们可以将所有的平行分量和垂直分量分别相加,从而得到空间平行力系的总平行力和总垂直力。
3. 其他因素:除了平行力和垂直力,还要考虑力矩、力的作用点和结构的几何形状
等因素。
这些因素可以通过另外一些理论和方法进行计算和分析。
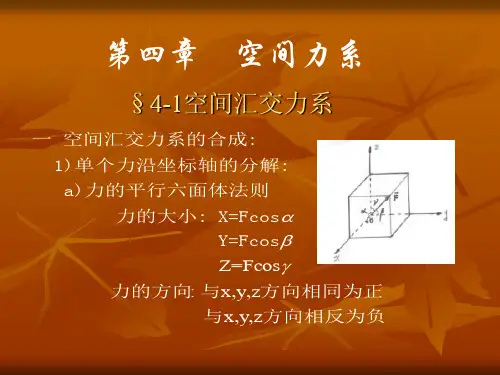


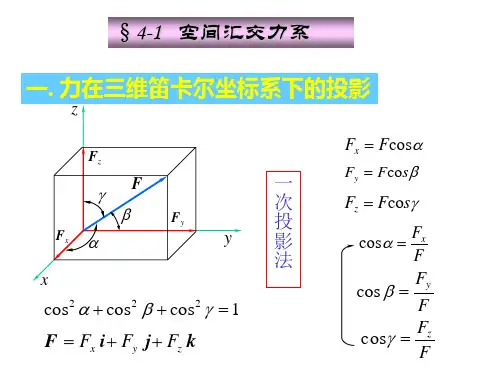

第四章空间力系一、要求1、能熟练地计算力在空间直角坐标轴上的投影和力对轴之矩。
2、对空间力偶的性质及其作用效应要有清晰的理解。
3、了解空间力系向一点简化的方法和结果。
4、能应用平衡条件求解空间汇交力系、空间任意力系、空间平行力系的平衡问题。
5、能正确地画出各种常见空间约束的约束反力。
二、重点、难点1、本章重点:力在空间直角坐标轴上的投影和力对轴之矩。
空间汇交力系、空间任意力系、空间平行力系的平衡方程的应用。
各种常见的空间约束及约束反力。
2、本章难点:空间矢量的运算,空间结构的几何关系与立体图。
三、学习指导1、空间力系的基本问题及其研究方法空间力系研究的基本问题仍然是静力学的三个基本问题,即:物体的受力分析、力系的等效替换和力系的平衡条件。
空间力系是力系中最普遍的情形,其它各种力系都是它的特殊情形。
按由浅入深、由特殊到一般的认识规律研究空间力系,是从理论上对静力学作一个系统而完整的总结。
与平面力系的研究方法相似,这里也采用力向一点平移的方法将空间任意力系分解为空间汇交力系和空间力偶系,再应用这两个力系的合成方法来简化原力系,然后根据简化结果推导出平衡条件。
由于空间力系各力作用线分布在空间,因而使问题复杂化。
出现了力在坐标轴上的二次投影法、力对轴的矩以及用向量表示力对点的矩和力偶矩等新问题,简化的结果和平衡方程也复杂了。
2、各类力系的平衡方程各类力系的独立的平衡方程的数目不变。
但是平衡方程的形式可以改变。
上表列出的是一般用形式。
解题指导1、对于解力在直角坐标轴上投影或力沿直角坐标轴分解这类问题,重要的是确定力在空间的位置。
一般解题的思路如下:(1)认清题意,仔细查看结构(或机构)的立体图,它由哪些部件组成,各部件在空间的位置,以及它们和坐标轴的关系。
(2)认清力的作用线在结构(或机构)的哪个平面内,寻找它与坐标面的交角,然后找力与坐标平面的夹角及力与坐标轴的夹角。
(3)考虑用一次投影或二次投影的方法求解。
2、计算力对轴之矩,一般令矩轴位于一个坐标面内,寻找与矩轴垂直的平面,然后按题意选择以下两种方法:(1)将力投影到垂直于轴的平面上,然后按平面上力对点的矩计算。
怎样将力投影到平面上呢?可先由力的作用点向平面作垂线,再寻找力和垂线所在平面与该平面的交线,然后将力向交线投影。
(2)将力沿直角坐标轴分解,然后根据合力之矩定理计算。
怎样选择分解方向呢?一般让两个分力在与矩轴垂直的平面内,一个分力平行于矩轴。
3、空间力系的解题技巧有以下两点:(1)平衡力系在任意轴上的投影等于零,在选择三个投影轴时,可不相交,可不相互垂直,但三轴不能共面,任意二轴也不能平行。
如果所选投影轴垂直于未知力或它所在的平面,则可减少平衡方程中未知力的数量,便于求解方程。
(2)平衡力系对任意轴的力矩都必须等于零,在选择三个力矩轴时,可不相交。
可不相互垂直。
另外,用力矩方程也能保证合力为零,可用力矩方程代替投影方程。
因此,空间力系的平衡方程可以有四矩式、五矩式、六矩式。
如果所选取的矩轴与未知力平行或通过几个未知力(或力的作用线)的交点,则可使平衡方程中的未知力的数量减少,便于求解方程。
四、典型例题解析例题4. 1 空间平行力系简化的结果是什么?可能合成为力螺旋吗?解答:空间平行力系简化的中间结果仍为一主矢和主矩(主矢与主矩垂直),简化的最后结果可为一合力、合力偶或平衡,唯独不可能是力螺旋。
因主矢与主矩相垂直。
例题4. 2 (1)空间力系中各力的作用线平行于某一固定平面;(2)空间力系中各力的作用线分别汇交于两个固定点。
试分析这两种力系各有几个平衡方程?解答:(1)空间力系中各力的作用线平行于某一固定平面,取某轴垂直于此固定平面,则各力在此轴的投影均为零,此方程失去使用价值,所以此力系的平衡方程个数等于或小于五个。
(2)空间力系中各力的作用线分别汇交于两个固定点,过这两点做一轴,此力系各力对此轴的力矩均为零,此方程失去求解价值,所以此力系的平衡方程个数等于或小于五个。
例题4. 3 传动轴用两个止推轴承支持,每个轴承有三个未知力,共6个未知量。
而空间任意力系的平衡方程恰好有6个,是否为静定问题?解答:此问题为静不定问题,因为六个轴承约束反力对此轴的力矩均为零,此力系的独立方程为五个。
例题4. 4空间任意力系向两个不同点简化,试问下述情况是否可能:(1)主矢相等,主矩也相等;(2)主矢不相等,主矩相等;(3)主矢相等,主矩不相等;(4)主矢、主矩都不相等。
解答:空间任意力系的主矢与简化中心无关,所以若向不同的点简化,主矢不相等是不可能的,因此(2)、(4)两种情况是不可能的。
空间任意力系的主矩一般与简化中心有关,所以(3)是可能的。
(1)主矢相等、主矩也相等也是可能的(两点均在主矢作用线上)。
例题4. 5 一均质等截面直杆的重心在哪里?若把它弯成半圆形,重心的位置是否改变?解答:在几何形心上(杆长一半处),若把它弯成半圆形,重心的位置改变。
例题4.6 当物体质量分布不均匀时,重心和几何中心还重合吗?为什么?解答:一般不重合。
因为几何中心只与物体的几何形状有关,而物体的重心与物体的质量分布有关,这是两个不同的概念与不同的度量。
例题4. 7 计算一物体重心的位置时,如果选取的坐标系不同,重心的坐标是否改变?重心在物体内的位置是否改变?解答:同一点在不同的坐标系里,其坐标是不同的,所以,计算物体的重心位置时,如果选取的坐标系不同,重心的坐标要改变。
重心在物体内的位置不会因坐标系的选择不同而改变。
例题4. 8 已知N F 1001= ,N F 3002=,N F 2003=,作用位置及尺寸如下图所示;求 力系向O 点简化的结果。
解:力系主矢在轴上的投影为:N F F FF xRx 4.345cos sin 32-=--==∑βαN F F F yRy 6.249cos 2===∑α N F F F F zRz56.10sin 31=-==∑β力系对O 点的主矩在轴上的投影为:m N F F M M xO x ⋅-=⋅-⋅-==∑78.51300sin 100cos )(32βαF m N F F M M y O y⋅-=⋅-⋅-==∑65.36100sin 200cos )(21ααF m N F F M M z O z ⋅=⋅+⋅==∑6.103300cos 200cos )(32βαF力系向O 点简化所得的力R F 和力偶O M 的各个分量如图)(b 所示。
)(a )(b 图题8.4yRxF OxyzRyF RzF oxM oyM oz M例题4. 9 已知小正方格的边长为mm 10,各力的大小及作用线位置如图所示;求力系的合力。
解:该平行力系的合力为)(202015101015↑=+-+-===∑N FF F zRz R设合力R F 与平面的交点为),(C C y x ,由合力矩定理有:mmN MM x R x ⋅=⨯+⨯-⨯+⨯-⨯==∑65050204015301020101015)()(F Fmm NMM y R y ⋅-=⨯-⨯-⨯+⨯-==∑12002020301010104015)()(F F由RZ C R x F y M =)(F ,RZ C R y F x M -=)(F 解出:mm F M x RzR y C 60)(=-=F , mm F M y RzR x C 5.32)(=-=F 力系的合力R F 如图中所示。
例题4. 10 已知G 处受力F 作用,板和杆的自重不计;求各杆的内力。
解:板的受力如图,由0)(=F AE M 、0)(=F CD M 以及0)(=F BF M ,分别得04=F ,06=F ,02=F再由0)(=F EF M ,05005001=--F F0)(=F GF M ,010********=+F F 0)(=F DE M ,010*******=--F F ,得 F F -=1(压),F F =3,F F -=5(压)图题9.4)(a )(b 图题11.4例题4. 11 下图所示均质矩形板ABCD 重为W ,用球铰链A 和碟形铰链(活页)B 固定在墙上,并用绳索CE 维持在水平位置。
已知α=∠=∠BAC ECA 。
试求绳索所受张力及A 、B 处的约束力。
解:分析矩形板的受力。
由于蝶形铰B 水平放置,可认为它不能限制板沿y 轴的轴向位移,故),(Bz Bx RB F F F =;球铰A 处的约束力),,(Az Ay Ax RA F F F F =。
于是板所受未知力=RB F),,,,,(T Bz Bx Az Ay Ax R F F F F F F F =。
为了尽量做到由一个平衡方程求解一个未知力,需要灵活选用平衡方程,特别是力对轴之矩形式的平衡方程:0)(∑=F Mz , 0=Bx F (1)0)(∑=F M y ,0sin 222=⋅-⨯l F l W T α,αsin 2WF T =(2) 0)(∑=F M x , 0sin 211=+⋅+⨯-Bz T F l F l W α, (3) 将式(2)代入式(3),得0=Bz F 。
进而有图题10.40∑=x F ,0sin cos =⋅-ααT Ax F F ,α2sin 21T Ax F F =( 4) 0∑=y F ,0cos cos =⋅-ααT Ay F F ,α2cos T Ay F F = ( 5)0∑=zF,0sin =+-αT Az F W F ,αsin T Az F W F -= (6)灵活选用平衡方程,往往可以避免求解联立方程。
与考察二维刚体的平衡问题相似,最好采用力对轴之矩形式的平衡方程。
因此,选择哪一根轴便很有考究。
例如,为求Bz F 可选AC为取矩轴,于是有0)(∑=F AC M, 0=Bz F显然,此式比式(3)简单。
由计算结果可知,0=RB F 。
这样,矩形板就可看成在ACE 平面内只受三力),,(RA T F F W 作用的系统,这时空间力系化为平面力系。
当然,此三力应汇交于该平面内一点O ,如图)(b 所示。
例题4. 12 已知力偶2M 与3M ,曲杆自重不计;求使曲杆保持平衡的力偶矩1M 和支座A 、D 的反力。
解 曲杆整体受力如图,由平衡方程∑=xF, 0=Dx F 0)(∑=F My ,02=-⨯M F a Az∑=zF, 0=-Dz Az F F0)(∑=F M z,03=-Ay aFM 0∑=y F , 0=-D yAyF F 0)(∑=F M x ,01=--c F bFM D y D z解得:0=DxF ,a M F Az 2=,aMF Dz 2=3M a c +图题12.4Dz例题4. 13 已知等边三角形板的边长为a ,在板内作用一矩为M 的力偶,板、杆的自重不计;求各杆的内力。