5第一节 复阻抗的串联与并联
- 格式:doc
- 大小:240.06 KB
- 文档页数:3

电化学阻抗谱(EIS)是一种用于研究电化学反应的强大工具,它可以通过测量电极上的交流电压和电流,获得电化学系统的信息。
在实际应用中,我们经常需要对EIS数据进行分析和模拟,以便更好地理解电化学系统的特性和行为。
在这篇文章中,我们将讨论EIS的等效电路模型,重点探讨串联和并联原则。
一、EIS的等效电路模型1. EIS的等效电路模型是通过对电化学系统的响应特性进行建模而得到的,它可以帮助我们推断电极界面和电解质中的各种传输过程,并从中获得有价值的信息。
2. 通常,EIS的等效电路模型可以分为两大类:基于传输过程的模型和基于电化学反应的模型。
其中,基于传输过程的模型将电极界面和电解质中的各种传输过程抽象为电阻和电容等元件,用以描述传质和传量的相互作用。
而基于电化学反应的模型则将电极界面上的电化学反应描述为电化学反应速率和电化学反应平衡等元件,用以描述电荷传递和功率损失的过程。
二、EIS的等效电路模型中的串联原则1. 在EIS的等效电路模型中,串联原则是指将电路中的各种电阻、电容和电感等元件按照串联的方式组合起来,以描述电化学系统中的传输和响应特性。
2. 以基于传输过程的模型为例,我们可以将电极界面的传质过程抽象为串联的电阻和电容元件,分别代表电解质的电导和电荷传递的速率;而电解质中的传质过程则可以抽象为另外一组串联的电阻和电容元件,分别代表电解质的电导和传输的速率。
通过串联原则,我们可以组合这些元件,描述电解质中和电极界面的传输过程。
三、EIS的等效电路模型中的并联原则1. 与串联原则相对应的是并联原则,它指的是将电路中的各种元件按照并联的方式组合起来,以描述电化学系统中的并行和响应特性。
2. 以基于电化学反应的模型为例,我们可以将电极界面上的电化学反应速率和电化学反应平衡抽象为并联的电阻和电容元件,分别代表反应速率和反应平衡过程的响应特性。
通过并联原则,我们可以组合这些元件,描述电极界面上的电化学反应过程。

《电路基础》阻抗的串联、并联和混联实验一. 实验目的1. 通过对电阻器、电感线圈、电容器串联、并联和混联后阻抗值的测量,研究阻抗串、并、混联的特点。
2. 通过测量阻抗,加深对复阻抗、阻抗角、相位差等概念的理解。
3. 学习用电压表、电流表结合画向量图法测量复阻抗。
二. 原理说明1. 交流电路中两个元件串联后总阻抗等于两个复阻抗之和,即:Z总=Z1+Z2两个元件并联,总导纳等于两个元件的复导纳之和,即:Y总=Y1+Y2两个元件并联,然后再与另一个元件串联,则总阻抗应为:Z总=Z3+2121ZZZZ2. 在实验十六中,用V、A、φ表法或V、A、W表法测元件阻抗是很方便的,但如果没有相位表和功率表,仅有电压表和电流表而又欲测复阻抗,则可以用下面所述的画向量图法来确定相位角。
如果图16-1的电阻器和电感线圈的复阻抗有待测量,可以用电压表分别测出有效值U、UR 、UrL,用电流表测出电流有效值I,(电阻R的感性分量可忽略不计,阻性分量计算根据实验十六实际值代入。
)图16-1绘制向量图如图16-2所示。
在绘制向量图时,由于相位角不能测出,只好利用电压U、UR、U rL 组成闭合三角形,根据所测电压值按某比U rLU L U例尺(如每厘米表示3V)截取线段,用几何φφrL方法画出电压三角形,然后根据电阻器的电压R r 与电流同相位,确定画电流向量的位置,电流的图16-2 比例尺也可以任意确定(如每厘米0.1A)。
根据电压表、电流表所测得的值以及从画出的向量图用量角器量出的相位角值,显然可得出复阻抗ZAB 、ZBC及串联后的总阻抗ZAC,从而得出R、L的值。
这种方法也适用于阻抗并联,可以根据上述相似的办法画出电流三角形,再根据其中一支路元件的电压与电流相位关系确定电压向量。
为了使从图中量出的角度精确,建议作图应大一些,即选取电流比例尺小一些,如每厘米代表0.1A 或0.05A。
三. 仪器设备名称数量型号1. 调压器 1台 0-24V2. 相位表/电量仪 1台3. 交流电压、电流表/电量仪 1套4. 万用表 1个5. 电阻器 1个 15Ω*16.电感线圈 1个 28mH*17.电容器 1个 220μF*1四. 任务与步骤1. 研究阻抗的串联、并联和混联(说明:以下所说的电阻器、电感线圈和电容器是指在实验十六中测试过的元件根据实验十六的表1可计算出它们的复阻抗Z1、Z2、Z3或复导纳Y。


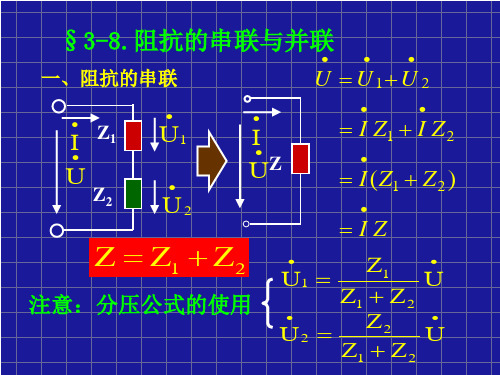

第五节 复阻抗的连接一、阻抗的串联如图9-3所示阻抗串联电路。
n 个复阻抗串联可以等效成一个复阻抗Z = Z 1 + Z 2 + … + Z n例如R-L-C 串联电路可以等效一只阻抗Z ,根据Z R = R,Z L = j X L ,Z C = -j X C ,则ϕωωj e j )1(j )(j Z X R CL R X X R Z Z Z Z C L C L R =+=-+=-+=++=即 Z =|Z |/ϕ其中电抗X = X L - X C ,阻抗大小为 2222)(C L X X R X R Z -+=+=ϕ 为阻抗角,代表路端电压u 与电流i 的相位差,即R X i u arctan=-=ϕϕϕ解:等效复阻抗Z = Z R + Z L = R + j X L = R + j ωL = 3 + j4 = 5/53.1︒ Ω,其中X L = 4 Ω,正弦交流电压u 的相量为=U220/30︒ V , 电路中电流相量为5220==Z U I /30︒-53.1︒= 44/-23.1︒ A 电阻上的电压相量和瞬时值分别为==I R U R132/-23.1︒ V , 2132=R u sin(314t - 23.1︒) V电感上的电压相量和瞬时值分别为===I X I Z U L L L j 176/90 - 23.1︒ = 176/66.9︒ V ,2176=L u sin(314t + 66.9︒) V二、阻抗的并联阻抗并联电路如图9-4所示。
图9-3 阻抗串联电路图9-4 阻抗并联电路n 只阻抗Z 1、Z 2、…、Z n 并联电路,对电源来说可以等效为一只阻抗,即nZ Z Z Z 111121+++= 即等效复阻抗Z 的倒数,等于各个复阻抗的倒数之和。
为便于表达阻抗并联电路,定义复阻抗Z 的倒数叫做复导纳,用符号Y 表示,即ZY 1= 导纳Y 的单位为西门子(S)。
于是有Y = Y 1 + Y 2 + … + Y n即几只并联导纳的等效导纳Y 等于所有导纳之和。
阻抗的串并联公式阻抗是电路中电阻和电感、电容元件的总体抵抗性质的综合,是交流电路分析的重要参数之一。
在电路中,阻抗可以通过串、并联的方式来计算。
下面,我们就来详细介绍一下阻抗的串并联公式。
串联阻抗公式:在电路中,若存在多个电阻、电感、电容元件串联在一起,则构成了一个串联电路。
串联电路中,电流在各个元件中依次通过,在通过每个元件时,电流大小相同,但电压不同,各个电阻、电感、电容元件的阻抗(Z)相互叠加。
其串联阻抗公式为:Ztotal = Z1 + Z2 + Z3 + …… + Zn其中,Z1,Z2,Z3……Zn 分别为串联电路中的每个电阻、电感、电容的阻抗。
并联阻抗公式:在电路中,若存在多个电阻、电感、电容元件并联在一起,则构成了一个并联电路。
并联电路中,各个元件的电压相同,但电流大小不同,各个电阻、电感、电容元件的阻抗(Z)相互叠加产生了等效的总阻抗。
其并联阻抗公式为:1/Ztotal = 1/Z1 + 1/Z2 + 1/Z3 + …… + 1/Zn其中,Z1,Z2,Z3……Zn 分别为并联电路中的每个电阻、电感、电容的阻抗。
串并联的综合:对于大多数复杂电路,既有串联电路,又有并联电路,因此需要用串联、并联的综合公式来计算。
在这种情况下,需要先计算出各个串联电路的总阻抗,然后将所得结果作为各并联电路的元件之一,最后使用并联阻抗公式计算总阻抗。
此外,在电路中几乎所有元件都具有一定的阻抗,因此串并联的公式应用非常广泛,特别是在高频电路和通信电路中经常需要使用串并联公式进行分析计算。
因此,对于工程师和电子学爱好者来说,深入理解串并联公式的原理和应用是非常必要的。