计算斜齿圆柱齿轮传动的接触应力

1.1.1 圆柱斜齿轮传动的设计计算已知输入功率1 1.5kWP =（略大于小齿轮的实际功率），小齿轮的转速为：12800rpm n =，大齿轮的转速为2560rpm n =，传动比5i =。

1.选定齿轮类型、精度等级、材料及齿数（1）由于第二级为圆锥齿轮传递，为了平衡锥齿轮传动对第二轴产生的轴向力，第一级传动设计为斜齿轮传动。

（2）叉车车速不高，为一般机械，故选用8级精度。

（3）材料选择，小齿轮材料为40Cr （正火），硬度为280HBW ，大齿轮材料为45钢（调质），硬度为240HBW ，二者材料硬度相差40HBW ，在30~50HBW 范围内。

（4）选小齿轮齿数12117,51785z z u z ==⋅=⨯=则，为了延长齿轮工作寿命，1z 和2z 尽量互质，所以校正2z 值，取284z =， 4.94u =。

2.按齿面接触疲劳强度设计因为是软齿面传动，故按齿面接触疲劳强度进行设计。

公式如下：1d ≥(5-1) 式中各参数为： （1）小齿轮传递的转矩 ()66111 1.5/N mm 9.55109.55105116.12800P T n ⋅=⨯=⨯⋅= (5-2) （2）设计时，因为v 值未知，v K 不能确定，故可初选载荷系数 1.1~1.8t K =，本设计中初选 1.4t K =。

（3）选取齿宽系数 1d φ=。

（4）查得材料弹性影响系数E Z =（5）初选螺旋角12β=︒，由机械手册查得节点区域系数 2.46H Z =。

（6）由选定齿数及齿数比，得端面重合度：121111=1.88 3.2cos 1.88 3.2cos12 1.631784z z αεβ⎡⎤⎛⎫⎡⎤⎛⎫-+=-+︒=⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎣⎦⎝⎭⎣⎦ (5-3) 得轴面重合度：10.318tan 0.318117tan12 1.53d z βεφβ==⨯⨯⨯︒= (5-4)由机械手册查得重合度系数0.768Z ε=。

设计一对斜齿圆柱齿轮传动。

已知传递功率P 1=130KW ，转速n 1=11460r/min, z 1=23, z 2=73,寿命L h=100h ，小齿轮做悬臂布置，使用系数K A=1.25解：1.选定齿轮类型、精度等级、材料及齿数 1） 斜齿圆柱齿轮2） 由10-8 P210 选择6级精度3） 材料选择。

齿轮要求质量小，传动功率大和可靠性高，因此必须选择力学性能高，表面硬化处理的高强度合金钢。

尺寸较小且要求较高，故采用锻造（锻钢）毛坯。

选用材料20Cr2Ni4,该材料的热处理方法是渗碳后淬火，MPa MPa s B1100,1200==σσ，芯部硬度350HBS,齿面硬度58-62HRC.4） 由题小齿轮齿数z 1=23，大齿轮齿数z 2=73，传动比为i=3.175） 初步选择螺旋角β=14°(螺旋角不宜过大，以减小轴向力Fa=Ft*tan β) 2.按齿面接触强度设计 按式试算，即d t 1≥[]231)(12H E H d t Z Z u u T K σεφα± (1) 确定公式内的各计算数值 1） 试选载荷系数βαK K K K K v A t***==1.62） 由表查得齿宽系数d φ=1b d =0.5(小齿轮做悬臂布置)3） 计算小齿轮传递的转矩T=113*10*9550n P =11460130*10*95503=1.08*105 N ·mm4） 由表查得材料的弹性影响系数E Z =189.8 Mpa 21（两个锻钢齿轮配对）5） 由图选取区域系数H Z =2.4336） 由图查得1αε=0.77，2αε=0.87，则αε=1αε+2αε=1.64 7） 由图按齿面硬度查得小齿轮的接触疲劳强度极限为1lim H σ=1650Mpa ，大齿轮的接触疲劳强度极限2lim H σ=1650Mpa8） 由式计算应力循环次数h jL n N 1160==60*11460*1*100=6.876*10717.310*876.6712==i N N =2.17*1079) 由图取接触疲劳寿命系数1HN K =1.15，2HN K =1.25（渗碳淬火钢）10) 计算接触疲劳许用应力取失效率为1%，安全系数为S=1，由式10-12 P205得S K HN H 1lim 11][σσ==1.15*1650Mpa=1897.5Mpa SK HN H 2lim 22][σσ==1.25*1650Mpa=2062.5Mpa则许用接触应力为：2][][][21H H H σσσ+==25.20625.1897+Mpa=1890Mpa(2) 计算1） 试算小齿轮分度圆的直径t d 1,由公式得3251)18908.189*433.2(*17.317.4*64.1*5.010*08.1*6.1*2≥t d mm =32mm2） 计算圆周速度 1000*6011n d v t π==19.2m/s3） 计算齿宽b 及模数nt m齿宽 t d d b 1φ==0.5*32mm=16mm模数 11cos z d m tnt β==2314cos *32o mm=1.43mm齿高 h=2.25nt m =2.25*1.43mm=3.2mm 26.505.43.21==hb4) 计算纵向重合度βεβφεβtan 318.01z d ==0.318*0.5*23*o 14tan =0.915) 计算载荷系数K 已知使用系数A K =1.25；由表10-3 P195查得齿间载荷分配系数1.1==ααF H K K ；(mm N mm N RbTK A /100/3.527>=)由表查得接触疲劳强度计算的齿向载荷分布系数βH K =1.1； 根据v=19.2m/s 和6级精度由图10-8 P194查得动载系数12.1=v K ；由图查得弯曲强度计算的齿向载荷分布系数βF K =1.14. 故载荷系数K=A K vK αH K βH K =1.25*1.12*1.1*1.1=1.694K 与t K 相近，故不必按实际的载荷系数校正所算得的分度圆直径。

11-4直齿圆柱齿轮传动的作用力及计算载荷：一、齿轮上的作用力：为了计算齿轮的强度，设计轴和选用轴承，有必要分析轮齿上的作用力。

当不计齿面的摩擦力时，作用在主动轮齿上的总压力将垂直于齿面，（因为齿轮传动一般都加以润滑，齿轮在齿啮合时，摩擦系数很小，齿面所受的摩擦力相对载荷很小，所以不必考虑），即为P175图11-5b所示的Fn（沿其啮合线方向），Fn可分解为两个分力：圆周力：Ft=2T1/d1 N径向力：Fr=Fttgα N而法向力：Fn=Ft/cosα NT1：小齿轮上的扭矩 T1=9550000p/n1 n·mmP：传递的功率（KW） d1：小齿轮分度圆直径 mmα：压力角 n1：小齿轮的转速(r·p·m)Ft1：与主动轮运动方向相反；Ft2与从动轮运动方向一致。

各力的方向 Fr：分别由作用点指向各轮轮心。

Fn：通过节点与基圆相切（由法切互为性质）。

根据作用力与反作用力的关系，主从动轮上各对的应力应大小相等，方向相反。

二、计算载荷：Fn是根据名义功率求得的法向力，称为名义载荷，理论上Fn沿齿宽均匀分布，但由于轴和轴承的变形，传动装置的制造安装误差等原因，载荷沿齿宽的分布并不均匀，即出现载荷集中现象（如P176图11-6所示，齿轮相对轴承不对称布置，由于轴的弯曲变形，齿轮将相互倾斜，这时，轮齿左端载荷增大，轴和轴承刚度越小，b越宽，载荷集中越严重。

此外，由于各种原动机和工作机的特性不同，齿轮制造误差以及轮齿变形等原因，还会引起附加动载荷。

精度越低，圆周速度V越大，附加载荷越大。

因此在计算强度时，通常以计算载荷K·Fn代替名义载荷Fn，以考虑上两因素的影响。

K—载荷系数表达式11-311-5 直齿圆柱齿轮的齿面接触强度计算：一、设计准则：齿轮强度计算是根据齿轮失效形式来决定的，在闭式传动中，轮齿的失效形式主要是齿面点蚀，开式传动中，是齿轮折断，在高速变截的齿轮传动中，还会出现胶合破坏，因胶合破坏的计算方法有待进一步验证和完善。

1. 齿面接触疲劳强度的计算齿面接触疲劳强度的计算中，由于赫兹应力是齿面间应力的主要指标，故把赫兹应力作为齿面接触应力的计算基础，并用来评价接触强度。

齿面接触疲劳强度核算时，根据设计要求可以选择不同的计算公式。

用于总体设计和非重要齿轮计算时，可采用简化计算方法；重要齿轮校核时可采用精确计算方法。

分析计算表明，大、小齿轮的接触应力总是相等的。

齿面最大接触应力一般出现在小轮单对齿啮合区内界点、节点和大轮单对齿啮合区内界点三个特征点之一。

实际使用和实验也证明了这一规律的正确。

因此，在齿面接触疲劳强度的计算中，常采用节点的接触应力分析齿轮的接触强度。

强度条件为：大、小齿轮在节点处的计算接触应力均不大于其相应的许用接触应力，即：⑴圆柱齿轮的接触疲劳强度计算1）两圆柱体接触时的接触应力在载荷作用下，两曲面零件表面理论上为线接触或点接触，考虑到弹性变形，实际为很小的面接触。

两圆柱体接触时的接触面尺寸和接触应力可按赫兹公式计算。

两圆柱体接触，接触面为矩形（2axb），最大接触应力σHmax位于接触面宽中线处。

计算公式为：接触面半宽:最大接触应力:•F——接触面所受到的载荷•ρ——综合曲率半径，（正号用于外接触，负号用于内接触）•E1、E2——两接触体材料的弹性模量•μ1、μ2——两接触体材料的泊松比2）齿轮啮合时的接触应力两渐开线圆柱齿轮在任意一处啮合点时接触应力状况，都可以转化为以啮合点处的曲率半径ρ1、ρ2为半径的两圆柱体的接触应力。

在整个啮合过程中的最大接触应力即为各啮合点接触应力的最大值。

节点附近处的ρ虽然不是最小值，但节点处一般只有一对轮齿啮合，点蚀也往往先在节点附近的齿根表面出现，因此，接触疲劳强度计算通常以节点为最大接触应力计算点。

参数直齿圆柱齿轮斜齿圆柱齿轮节点处的载荷为综合曲率半径为接触线的长度为，3）圆柱齿轮的接触疲劳强度将节点处的上述参数带入两圆柱体接触应力公式，并考虑各载荷系数的影响，得到：接触疲劳强度的校核公式为：接触疲劳强度的设计公式为：•KA——使用系数•KV——动载荷系数•KHβ——接触强度计算的齿向载荷分布系数•KHα——接触强度计算的齿间载荷分配系数•Ft——端面内分度圆上的名义切向力，N；•T1——端面内分度圆上的名义转矩，N.mm；•d1——小齿轮分度圆直径，mm；•b ——工作齿宽，mm，指一对齿轮中的较小齿宽；•u ——齿数比；•ψd——齿宽系数，指齿宽b和小齿轮分度圆直径的比值（ψd=b/d1）。

《机械设计基础》填空部分复习题第九章1、机械零件由于某种原因，不能时，称为失效。

机械零件在的条件下，零件能安全工作的限度，称为工作能力。

2、若两个零件在受载前是接触或接触，受载后接触变形处为一小面积，在这小面积上产生的局部应力称为应力，如等零件工作时就有这种应力作用。

对高副接触的零件，在外载荷作用下，接触处将产生应力，从而将引起零件的破坏。

两零件高副接触时，其最大接触应力取决于，及度上的载荷。

两零件高副接触时，其接触应力随接触点，线处的曲率半径增大而；随材料的弹性模量减小而；随单位接触宽度载荷的增大而。

零件的表面硬度，接触表面的综合曲率半径，可以提高零件的接触疲劳强度。

2、材料发生疲劳破坏时的应力循环次数N必于该材料的循环基数N0；由于，和等因素的影响，零件的疲劳极限必小于其材料的疲劳极限。

3、随时间变化的应力称为变应力，具有周期性变化的变应力称为循环变应力。

按照随时间变化的情况，应力可分为和。

变应力可归纳为变应力、变应力和变应力三种基本类型。

变应力的五个基本参数是σmax、σmin、σm、σa、r。

应力循环中的与之比，可用来表示变应力中应力变化的情况，通常称为变应力的循环特性r。

当r=+1表示为应力，r=0表示为应力，它的σmin=，σm=σa=；当r=-1表示为应力，它的σmax=σa；σm=；非对称循环变应力的r变化范围为和之间。

4、在变应力中，表示与力循环次数之间的关系曲线称为材料的疲劳曲线。

在变应力作用下，零件的主要失效形式是。

在静应力下，塑性材料的零件按不发生条件进行强度计算，故应取材料的作为极限应力；而脆性材料的零件按不发生的条件进行计算，故应取材料的作为极限应力。

变应力下，零件的许用极限应力与零件材料的疲劳极限有关，同时还应考虑系数、__系数和系数。

6、一非对称循环变应力，其σmax=100N/mm2，σmin=-50N/mm2，计算其应力幅σa= N/mm2，平均应力σm=___N/mm2，循环特性r= 。

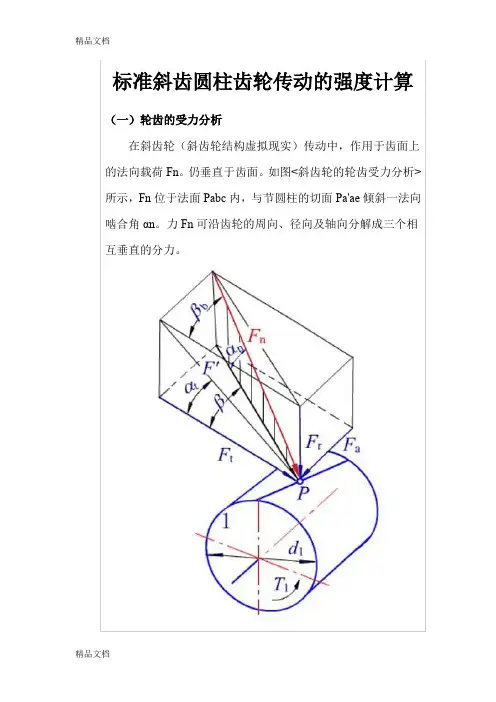
研究，可用
式中为斜齿轮传动的端面重合度
图<标准圆柱齿轮传动的端面重合度>
斜齿轮的纵向重合度可按以下公式计算:
斜齿轮计算中的载荷系数，其中使用系数
与齿向载荷分布系数的查取与直齿轮相同；动载系数可由图<动载系数值>中查取；齿间载荷分配系数与可根据斜齿轮的精度等级、齿面硬化情况和载荷大小由表<齿间载荷分配系数>中查取。

(三)齿根弯曲疲劳强度计算
如下图所示，斜齿轮齿面上的接触线为一斜线。

受载时，齿轮的失效形式为局部折断。

斜齿轮的弯曲强度，若按轮齿局部
斜齿轮的计算载荷要比直齿轮的多计入一个参数劳强度公式为：
、
ZH称为区域系数。

上右图为法面压力角αn=20°的标准齿轮的ZH值。

于是得
同前理，由上式可得
应该注意，对于斜齿圆柱齿轮传动，因齿面上的接触线是倾斜的（如右图），所以在同一齿面上就会有齿顶面(其上接触线段为e1P)与齿根面(其上接触线段为e2P)同时参与啮合的情况(直齿轮传动，齿面上的接触线与轴线平行，就没有这种现象)。

如前所述，齿轮齿顶面比齿恨面具有较高的接触疲劳强度。

设小齿轮的齿面接触疲劳强度比大齿轮的高(即小齿轮的材料
较好，齿面硬度较高)，那么，当大齿轮的齿根面产生点蚀，e2 P一段接触线已不能在承受原来所分担的载荷，而要部分地由齿顶面上的e1P一段接触线来承担时，因同一齿面上，齿顶面的接触疲劳强度较高，所以即使承担的载荷有所增大，只要还
为，当>1.23应取=1.23。

分度圆圆周力 材料接触应力 材料弯曲应力
承载能力计算
Ft σHlim σFE
93015.538 1300 18Cr2Ni4W 900
弧度
角度
传动比
t
1
端面模数 mt
6.0205
0.34906585
端面压力 角
αt
0.379139 21.72308008
0.41887902
βb 0.392184 22.47048266
161.50138 160.48751
136.762 135.749
分度圆直径 基圆直径 节圆直径 齿顶压力角 分度圆弧齿厚 重合度
滑动率
当量齿数 理论跨齿数 实际跨齿数 公法线长度
计算量棒直径 实际量棒直径
量棒中心所在圆上 的压力角
跨棒距
d=mt*cosβ db
ααt
ε=εα+εβ εα εβ η
630
计算中心距
244.493
分度圆直径
241.628 247.3578
计算法向模数
mn 5.93721
SIN（） COS()
TAN（）
ASIN （）
ACOS （）
ATAN() inv （）
0.3420201 0.9396926 0.36397023 0.35657 1.2142 0.3358 0.014904
0.4067366 0.9135455 0.44522869 0.43221 1.1386 0.3967 0.02635
0.370121 0.9289836 0.39841502 0.38887 1.1819 0.3624 0.019276
0.362053 0.9321575 0.38840325 0.37951 1.1913 0.3548 0.017934

圆柱齿轮传动的强度计算1 直齿圆柱齿轮传动的强度计算1.齿面接触疲劳强度计算为了保证在预定寿命内齿轮不发生点蚀失效，应进行齿面接触疲劳强度计算。

因此，齿轮接触疲劳强度计算准则为：齿面接触应力σH小于或等于许用接触应力σHP，即σH≤σHP赫兹公式由于直齿轮在节点附近往往是单对齿啮合区，轮齿受力较大，故点蚀首先出现在节点附近。

因此，通常计算节点的接触疲劳强度。

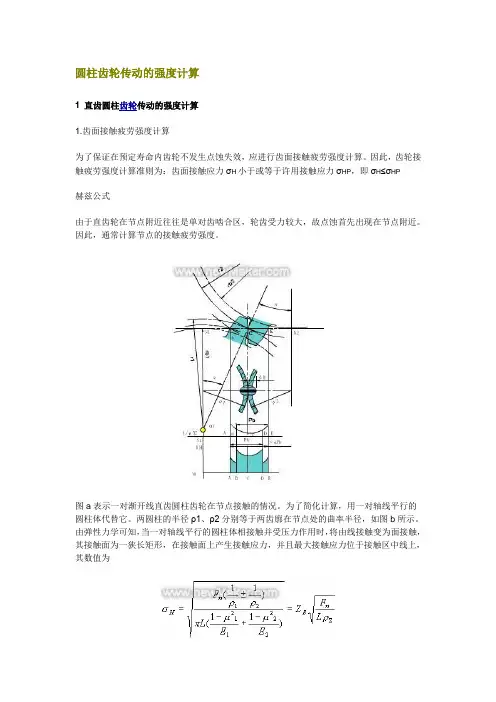
图a表示一对渐开线直齿圆柱齿轮在节点接触的情况。

为了简化计算，用一对轴线平行的圆柱体代替它。

两圆柱的半径ρ1、ρ2分别等于两齿廓在节点处的曲率半径，如图b所示。

由弹性力学可知，当一对轴线平行的圆柱体相接触并受压力作用时，将由线接触变为面接触，其接触面为一狭长矩形，在接触面上产生接触应力，并且最大接触应力位于接触区中线上，其数值为式中σH-接触应力（Mpa）Fn-法向力（N）L-接触线长度（mm）rS-综合曲率半径（mm）；±-正号用于外接触，负号用于内接触ZE-材料弹性系数（），，其中E1、E2分别为两圆柱体材料的弹性模量（MPa）；m1、m2分别为两圆柱体材料的泊松比。

上式表明接触应力应随齿廓上各接触点的综合曲率半径的变化而不同，且靠近节点的齿根处最大（图c、d）。

但为了简化计算，通常控制节点处的接触应力。

节点处的参数（1）综合曲率半径由图可知，，代入rE公式得式中：，称为齿数比。

对减速传动，u=i；对增速传动，u=1/i。

因，则有（2）计算法向力（3）接触线长度L引入重合度系数Ze，令接触线长度将上述参数代入最大接触应力公式得接触疲劳强度计算公式令，称为节点区域系数。

则得(1) 齿面接触疲劳强度的校核公式齿面接触疲劳强度的校核公式为(2) 齿面接触疲劳强度设计公式设齿宽系数，并将代入上式，则得齿面接触疲劳强度的设计公式式中:d1-小齿轮分度圆直径（mm）；ZE-材料弹性系数()，按下表查取；注：泊松比m1＝m2＝0.3Z H-节点区域系数，考虑节点处轮廓曲率对接触应力的影响，可由下左图查取。

2. 计算公式校核式：
F
KFtYFaYsaY bmn
F
设计式：
3. 参数取值说明
mn
3
2KT1Y cos2 d z12
YFaYsa
F
1)YFa、YSa---齿形系数和应力修正系数。Zv=Z/cos3 YFa、YFa
2) Y---螺旋角系数。
3) 初步设计计算
在设计式中，K等与齿轮尺寸参数有关，故需初步估算：
精品文档
第7节 标准斜齿圆柱齿轮的强度计算
一． 齿面接触疲劳强度计算
1. 斜齿轮接触方式 2. 计算公式 校核式： H ZE ZH
KFt bd1
u 1 u
H
设计式：
3. 参数取值说明
d1
3
2KT1 d
u
u
1
ZEZH
H
2
1) ZE---弹性系数 2) ZH---节点区域系数
3) ---斜齿轮端面重合度 4) ---螺旋角。斜齿轮：=80～250；人字齿轮=200～350
5. 6. 齿轮材料的选择及热处理的原则是什么？为什么？ 7. 已知直齿圆柱齿轮传动小齿轮分度圆直径、扭矩。Ft1=?、Fr1=?、
Fn1=?、Ft2=?、Fr2=?、Fn2=?。怎样确定方向？ 8. 已知斜齿圆柱齿轮传动小齿轮分度圆直径、扭矩。Ft1=?、Fr1=?、
Fa1=?、Fn1=?、Ft2=?、Fr2=?、Fa2=?、Fn2=?。 怎样确定方向？ 9. 齿轮传动中载荷系数包含哪几部分？它们的含义是什么？ 10. 何谓齿轮修缘？为什么要修缘？
5) 许用应力：[H]=([H1]+[H2])/21.23[H2] 6) 分度圆直径的初步计算
在设计式中，K等与齿轮尺寸参数有关，故需初步估算：

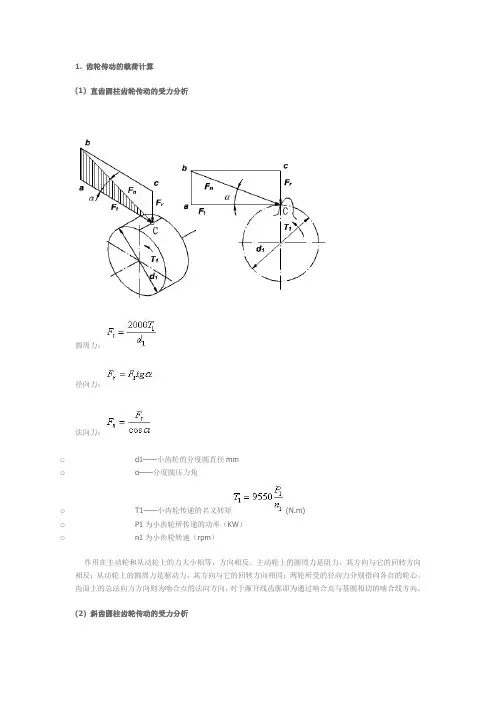
1. 齿轮传动的载荷计算(1) 直齿圆柱齿轮传动的受力分析圆周力：径向力：法向力：o d1——小齿轮的分度圆直径mmoα——分度圆压力角o T1——小齿轮传递的名义转矩(N.m)o P1为小齿轮所传递的功率（KW）o n1为小齿轮转速（rpm）作用在主动轮和从动轮上的力大小相等，方向相反。

主动轮上的圆周力是阻力，其方向与它的回转方向相反；从动轮上的圆周力是驱动力，其方向与它的回转方向相同；两轮所受的径向力分别指向各自的轮心。

齿面上的总法向力方向则为啮合点的法向方向，对于渐开线齿廓即为通过啮合点与基圆相切的啮合线方向。

(2) 斜齿圆柱齿轮传动的受力分析圆周力：径向力：轴向力：法向力：∙αt——端面分度圆压力角；∙αn——法向分度圆压力角；∙β——分度圆螺旋角；∙βt——基圆螺旋角。

(3) 直齿锥齿轮传动的受力分析法向力Fn集中作用在齿宽节线中点处，则Fn可分解为互相垂直的三个分力。

圆周力：径向力：轴向力：dm1——小齿轮齿宽中点分度圆直径mm；δ1——小锥齿轮分度圆锥角圆周力和径向力的方向判别与直齿圆柱齿轮判别方法相同，轴向力方向分别指向各自的大端。

由于锥齿轮传动两轴的空间交角为90°，因此存在以下关系：；。

负号表示方向相反。

(4) 齿轮传动的计算载荷齿轮承受载荷常表现为其传递的力矩或圆周力。

由上述力的分析计算所得出的圆周力为齿轮传动的名义圆周力。

实际工作中，由于各种因素的影响，齿轮实际承受的圆周力要大于名义圆周力。

考虑各种因素的影响，实际圆周力Ftc为：Ftc也称为计算载荷。

1）KA——使用系数。

2）KV——动载系数。

3) KHα和KFα——齿间载荷分配系数。

4) KHβ和KFβ——齿向载荷分布系数。

2. 齿轮传动应力分析齿轮传动工作过程中，相啮合的轮齿受到法向力Fn的作用，主要产生两种应力：齿面接触应力和齿根弯曲应力。

(1) 齿面接触应力σH齿轮传动工作中，渐开线齿面理论上为线接触，考虑齿轮的弹性变形，实际上为很小的面接触。

GB/T 3480.2—XXXX直齿轮和斜齿轮承载能力计算第2部分：齿面接触（点蚀）强度计算（征求意见稿）编制说明课题工作组2020年3月《直齿轮和斜齿轮承载能力计算第2部分：齿面接触(点蚀)强度计算》（征求意见稿）编制说明一、工作简况1任务来源本项目是根据国家标准化管理委员会制、修订国家标准项目计划（国标委综合[2010]年87号文），计划编号：20101311-T-469，项目名称“直齿轮和斜齿轮承载能力计算方法第2部分：齿面接触（点蚀）强度计算”进行修订，等同采用ISO 6336-2:2019，部分代替GB/T 3480—1997。

主要起草单位：郑州机械研究所有限公司、湖南大学、中机轨道交通装备科技有限公司、西安法士特汽车传动有限公司、山东华成中德传动设备有限公司、中机生产力促进中心、河南中豫远大重工科技有限公司、苏州绿控传动科技股份有限公司、郑州高端装备与信息产业技术研究院有限公司、江苏中工高端装备研究院有限公司。

计划完成时间：2020年6月。

GB/T 3480系列标准引进自ISO 6336系列。

ISO 6336在“直齿轮和斜齿轮承载能力计算”的总标题下包括以下5个部分：——第1部分：基本原理、概述和通用影响因素；——第2部分：齿面接触（点蚀）强度计算；——第3部分：轮齿弯曲强度计算——第5部分：材料的强度和质量——第6部分：变载荷条件下的使用寿命计算其中，GB/T 3480.1—2019（ISO 6336-1:2006,IDT ）、GB/T 3480.5—2008（ISO 6336-5:2006,IDT ）和GB/T 3480.6—2018（ISO 6336-6:2006,IDT ）已经先后发布，GB/T 3480.2—XXXX （ISO 6336-2:2019,IDT ）和GB/T 3480.3—XXXX （ISO 6336-3:2019,IDT ）已完成征求意见稿，现在开始向全社会征集修改意见。

《机械设计计算题》试题库29001单级齿轮减速器由电动机直接驱动，减速器输入功率P＝7.5kW，电动机转速n=1450r/min,齿轮齿数z1＝20，z2＝50，减速器效率?＝0.9。

试求减速器输出轴的功率和转矩。

所以，29002带式输送机的传动简图如下图所示，已知输送带输出功率为 2.51kW，现有Y100L2-4型电动机一台，电动机额定功率P ed=3kW，满载转速n m=1420r/min，试问此电动机能否使用。

各效率如下：?联轴器＝0.99，?齿轮＝0.97，?轴承＝0.99。

验算此电动机能否使用P输入＝P输出/?总＝2.51/0.895=2.805kWP ed(=3kW)>P输入（=2.805kW）此电动机能用。

29003带式输送机的传动简图如下图所示，已知输送带的工作拉力F＝2300N(F中已考虑输送带与卷筒、卷筒轴承的摩擦损耗的影响），输送带的速度v=1.1m/s，卷筒直径D＝400mm，齿轮的齿数为z1＝17，z2＝102，z3＝24，z4＝109，试求传动装置的输出功率、总效率、总传动比和输入功率。

各效率如下：?联轴器=0.99、?齿轮＝0.97、?轴承＝0.99。

1）输出功率：2）总效率：3）总传动比：4）输入功率29004一蜗杆减速器，蜗杆轴功率，传动总效率，三班制工作，如工业用电为每度0.12元，试计算五年（每年按260天计算）中用于功率损耗的费用。

功率损耗五年中损耗能量损耗费用元五年中用于功率损耗的费用为74880元。

29005下图为一卷扬机传动系统简图，已知：被提升的重物W＝5000N，卷筒直径D＝300mm，卷筒转速n G=25r/min，电动机转速n E＝720r/min，试求：1）重物W的上升速度v；2）卷筒的转矩T；3）匀速提升重物时卷筒的功率P；4）电动机所需功率P E（传动总效率?＝0.886）；5）减速器总传动比?i总。

1)2)3)4)5)29006 带式输送机的传动系统如下图所示，已知z1＝z3＝z5＝z7＝17，z2＝z4＝z6＝z8＝34，带轮直径D1＝125mm、D2=250mm，电动机转速n1=1440r/min，各效率为?轴承＝0.99、?带＝0.94、?齿轮＝0.97、?链＝0.96，求：1）电动机至卷筒之间的总效率；2）传动系统的传动比i总（电动机至卷筒）；3）卷筒的转速n8（即大链轮z8的转速）。

、 分别为Ⅰ点、Ⅱ点、Ⅲ点单位齿宽上所受的力。单位齿宽上的总载荷 + 。此时载荷分配率应为 。
+ = + + = +（ - ） +
（ - - ） = （ + + ）-( + ) -
受最大载荷的齿对上的载荷 为
= [ （ + + ）-( + ) - - +( + ) +
= [ +( + ) ]
= [1+ ]
一对啮合传动的齿轮，当同时有三对齿啮合时（如图）有两组基圆齿距 和 。对于第一组基圆齿距，有 和 ，其偏差为 。对第二组基圆齿距，有有 和 ，其偏差为 。啮合时，第一对齿在Ⅰ点接触，产生变形量达 时，第二对齿在Ⅱ接触并受力。当接触点（Ⅰ点和Ⅱ点）再变形 后，第Ⅲ点接触并受力，且有变形 （如图）。此时，第一对齿在Ⅰ点产生的变形量为 = + + ，第二对齿产生的变形量为 = + 。若这三对齿在啮合点的啮合刚度分别为 、 、 ，则有 = ， = ， = 。
对于斜齿圆柱齿轮传动,在ISO/DP6336中，当 <1时，取
当 >1时，取
齿间载荷分配系数取为
当 ≤2时
当 >2时
在ΓOCT21354-75中，当 0.9时，取
由下图决定。图中曲线上的数字表示根据ΓOCT1643-72按工作平稳性规范的精度等级。
在AGMA215.01中，没有考虑这两个系数。
在JGMA402.01中，当 ≤1时取
当 >1是，取
齿间载荷分配系数 取1。
有上述可知，JGMA402.01中取了 值大于1，而取 =1是不合理的，偏不安全的。由上图可知，在ΓOCT21354-75中 不但与精度等级有关，还和圆周速度有关。这主要是因为在决定载荷分配率λ是，在ΓOCT21354-75中以初始圆周力为基础的。齿间载荷分配情况与内部附加动载荷有关，集合圆周速度有关。在ISO和DIN的方法中， 是有包括外部附加动载荷在内的载荷 决定的。所以ΓOCT21354-75中速度对 的影响，实际上只反映了内部附加动载荷对 的影响。

例1 设计用于带式输送机传动装置的闭式单级直齿圆柱齿轮传动。

传递功率P=2.7kW ，小齿轮转速n 1=350r/min ，传动比i=3.57。

输送机工作平稳，单向运转，两班工作制，齿轮对称布置，预期寿命10年，每年工作300天。

解：1. 选择齿轮精度等级、材料、齿数1）带式输送机属于一般机械，且转速不高，故初选择8级精度。

2）因载荷平稳，传递功率较小，可采用软齿面齿轮。

参考表5-6，小齿轮选用45钢调质处理，齿面硬度220~250HBS ，σHLim1=595MPa ，σFE1=230MPa ；大齿轮选用45钢正火处理，齿面硬度170~200HBS ，σHLim2=520MPa ，σFE2=200MPa 。

3）初选小齿轮齿数z 1=24，则z 2=iz 1=3.57×24=85.68，取z 2=87。

故实际传动比i=z 2/z 1=87/24=3.62，与要求的传动比3.57的误差小于3%。

对于齿面硬度小于350 HBS 的闭式软齿面齿轮传动，应按齿面接触强度设计，再按齿根弯曲强度校核。

2. 按齿面接触强度设计设计公式5-481d ≥1）查表5-8，原动机为电动机，工作机械是输送机，且工作平稳，取载荷系数K=1.2。

2）小齿轮传递的转矩 112.79550955073.671350P N m n T =⨯=⨯=⋅3）查表5-13，齿轮为软齿面，对称布置，取齿宽系数φd =1。

4）查表5-10，两齿轮材料都是锻钢，故取弹性系数Z E =189.8 MPa 1/2。

5）两齿轮为标准齿轮，且正确安装，故节点区域系数Z H =2.5，取重合度系数Z ε=0.9。

6）计算许用接触应力 N W X HLim H HZ Z Z Sσσ⎡⎤=⎣⎦①应力循环次数小齿轮N 1=60n 1jL h =60×350×1×(2×8×300×10)=10.08×108 大齿轮N 2= N 1/i=10.08×108/3.62=2.78×108②据齿轮材料、热处理以及N 1、N 2，查接触疲劳寿命系数图表，不允许出现点蚀，得接触疲劳寿命系数Z N1=1，Z N2=1，两齿轮均为软齿面故ZW=1，ZX=1。

% 3-斜齿圆柱齿轮传动设计计算% 已知条件f=2000; % 输送带工作拉力(N)v=1.5; % 输送带工作速度(m/s)d=250; % 滚筒直径(mm)nu=0.97; % 斜齿圆柱齿轮传动效率i=3.5; % 齿轮副传动比hd=pi/180; % 角度换算成弧度的系数disp ' 'disp ' ========== 已知条件==========';fprintf(' 输送带工作拉力 f = %3.0f N \n',f);fprintf(' 输送带工作速度v = %3.2f m/s \n',v);fprintf(' 滚筒直径 d = %3.0f mm \n',d);fprintf(' 齿轮传动效率nu = %3.2f \n',nu);fprintf(' 齿轮副传动比i = %3.2f \n',i);% 采用硬齿面齿轮传动p2=f*v/1000; % 大齿轮传递功率(kW)n2=60*v*1e3/pi/d; % 大齿轮转速(r/min)p1=p2/nu; % 小齿轮传递功率(kW)n1=i*n2; % 小齿轮转速(r/min)chm=1500; % 试验齿轮接触疲劳极限(MPa)cfm=460; % 试验齿轮弯曲疲劳极限(MPa)chp=0.9*chm; % 试验齿轮许用接触应力(MPa)cfp=1.4*cfm; % 试验齿轮许用弯曲应力(单向传动) z1=18; % 小齿轮齿数(选取)z2=round(i*z1); % 大齿轮齿数u=z2/z1; % 齿数比pd=0.675; % 齿宽系数bat0=10; % 螺旋角初值t1=9550*p1/n1; % 小齿轮传递转矩(Nm)zv1=z1/(cos(bat0*hd))^3; % 小齿轮当量齿数zv2=u*zv1; % 大齿轮当量齿数ysf1=4.43; % 小齿轮齿形系数ysf2=3.88; % 大齿轮齿形系数if ysf1>=ysf2ysf=ysf1; % 确定计算齿形系数elseysf=ysf2;endk=1.6; % 载荷系数am=12.0; % 齿根弯曲强度计算系数(螺旋角范围15-25°) mnj=am*(k*t1*ysf/pd/z1^2/cfp)^(1/3); % 按照齿根弯曲强度计算模数(mm)if mnj<=2mn=2; % 确定标准模数(mm)elsemn=round(mnj+0.5)endaj=mn*z1*(1+u)/2/cos(bat0*hd);a=round(aj/5)*5+5; % 确定中心距(mm)bat=acos(0.5*mn*z1*(1+u)/a)/hd; % 确定螺旋角disp ' 'disp ' ========== 齿轮传动设计计算==========';fprintf(' 大齿轮传递功率p2 = %3.3f kW \n',p2);fprintf(' 大齿轮转速n2 = %3.3f r/min \n',n2);fprintf(' 小齿轮传递功率p1 = %3.3f kW \n',p1);fprintf(' 小齿轮转速n1 = %3.3f r/min \n',n1);fprintf(' 试验齿轮许用接触应力chp = %3.3f MPa \n',chp);fprintf(' 试验齿轮许用弯曲应力cfp = %3.3f MPa \n',cfp);fprintf(' 小齿轮齿数z1 = %3.0f \n',z1);fprintf(' 大齿轮齿数z2 = %3.0f \n',z2);fprintf(' 齿宽系数pd = %3.3f \n',pd);fprintf(' 齿数比u = %3.3f \n',u);fprintf(' 小齿轮传递转距t1 = %3.3f Nm \n',t1);fprintf(' 小齿轮当量齿数zv1 = %3.3f \n',zv1);fprintf(' 大齿轮当量齿数zv2 = %3.3f \n',zv2);fprintf(' 小齿轮齿形系数ysf1 = %3.3f \n',ysf1);fprintf(' 大齿轮齿形系数ysf2 = %3.3f \n',ysf2);fprintf(' 齿轮模数mn = %3.2f mm \n',mn);fprintf(' 中心距 a = %3.2f mm \n',a);fprintf(' 螺旋角bat = %3.3f °\n',bat);if bat>15 & bat<=25' @@@ 螺旋角在15-25°范围内,计算系数选择合适'else' @@@ 螺旋角超出15-25°范围,重新选择计算系数'endd1=mn*z1/cos(bat*hd); % 计算分度圆直径(mm)d2=u*d1;han=1.0; % 正常齿制cn=0.25;da1=d1+2*han*mn; % 计算齿顶圆直径(mm)da2=d2+2*han*mn;df1=d1-2*han*mn-2*cn*mn; % 计算齿根圆直径(mm)df2=d2-2*han*mn-2*cn*mn;b=pd*d1;b2=round(b/2)*2; % 确定齿宽(mm)b1=b2+6;ad=733; % 齿面接触强度计算系数(螺旋角范围15-25°)d1j=ad*(k*t1*(u+1)/pd/chp^2/u)^(1/3); % 按照齿面接触强度计算分度圆直径(mm) if d1j<=d1' @@@ 满足齿面接触强度要求'else' @@@ 不满足齿面接触强度要求,需要修改设计参数'endv=pi*d1*n1/6e4; % 齿轮圆周速度(m/s)fprintf(' 小齿轮分度圆直径d1 = %3.3f mm \n',d1);fprintf(' 齿顶圆直径da1 = %3.3f mm \n',da1);fprintf(' 齿根圆直径df1 = %3.3f mm \n',df1);fprintf(' 齿宽b1 = %3.0f mm \n',b1);fprintf(' 大齿轮分度圆直径d2 = %3.3f mm \n',d2);fprintf(' 齿顶圆直径da2 = %3.3f mm \n',da2);fprintf(' 齿根圆直径df2 = %3.3f mm \n',df2);fprintf(' 齿宽b2 = %3.0f mm \n',b2);计算结果：========== 已知条件==========输送带工作拉力 f = 2000 N输送带工作速度v = 1.50 m/s滚筒直径 d = 250 mm齿轮传动效率nu = 0.97齿轮副传动比i = 3.50========== 齿轮传动设计计算==========大齿轮传递功率p2 = 3.000 kW大齿轮转速n2 = 114.592 r/min小齿轮传递功率p1 = 3.093 kW小齿轮转速n1 = 401.070 r/min试验齿轮许用接触应力chp = 1350.000 MPa试验齿轮许用弯曲应力cfp = 644.000 MPa小齿轮齿数z1 = 18大齿轮齿数z2 = 63齿宽系数pd = 0.675齿数比u = 3.500小齿轮传递转距t1 = 73.643 Nm小齿轮当量齿数zv1 = 18.846大齿轮当量齿数zv2 = 65.961小齿轮齿形系数ysf1 = 4.430大齿轮齿形系数ysf2 = 3.880齿轮模数mn = 2.00 mm中心距 a = 85.00 mm螺旋角bat = 17.647 °@@@ 螺旋角在15-25°范围内,计算系数选择合适@@@ 满足齿面接触强度要求小齿轮分度圆直径d1 = 37.778 mm齿顶圆直径da1 = 41.778 mm齿根圆直径df1 = 32.778 mm齿宽b1 = 32 mm大齿轮分度圆直径d2 = 132.222 mm齿顶圆直径da2 = 136.222 mm齿根圆直径df2 = 127.222 mm齿宽b2 = 26 mm。

一、轮齿的接触应力ζj 的计算：ζj=0.418√FE(1/ρz+1/ρb )/bF=F1/(cos αcos β)F1=2Tg/dd 为节圆的直径Tg 为计算载荷ρz 、ρb 分别为主从动齿轮节点处的曲率半径：直齿轮：ρz=r z sin α ρb= r b sin α斜齿轮：ρz=（r z sin α）/cos 2β ρb=（ r b sin α）/cos 2βr z r b为主，从动齿轮节圆半径 二、轮齿弯曲应力ζw 的计算：直齿轮：ζw=F1K ζK f /bty=2TgK ζK f /πm 3ZK c y斜齿轮：ζw=2Tgcos βK ζ/∏m 3n ZK c yK εK ε为重合度系数，一般取K ε=2.0K ζ集中应力系数，一般直齿轮取K ζ=1.65，斜齿轮取K ζ=1.50y 为齿形系数，一般在0.16---0.18之间K c 为齿宽系数，一般在4.5---8.0之间K f 为摩擦力系数，主动轮取1.1，从动轮取0.9 A B δf Fa LbX一、初选轴的直径已知中心距A。

第二轴与中间轴中部直径：d≈0.45A，轴的最大直径d和支承间距离L的比值：d/L=0.16--0.18；对二轴：d/L=0.18--0.21；第一轴花键部分直径d可按下试初选：d=K 3√T emax式中，K为经验系数，K=4.0---4.6；T emax为发动机最大转矩（N.m）二、轴的强度计算1.轴的刚度计算：轴在垂直面内绕度：f c=F1a2b2/3EIL轴在水平面内绕度：f s=F2a2b2/3EIL轴在水平面内转角: δ=F1ab（b-a）/3EIL式中，F1为齿轮齿宽中间平面上的径向力（N）,F2为齿轮齿宽中间平面上的圆周力（N），E为弹性模量，E=2.1×105MPa；I为惯性矩（mm4），对于实心轴，I=πd4/64;d为轴的直径（mm），花键外按平均直径计算；a，b为齿轮上的作用力矩A,B的距离（mm），L为支座间的距离（mm）。

一、选择题(共20分，每小题2分)1、通常，一个零件的磨损过程大致可分为三个阶段，按先后顺序，它们依次是( D )A. 剧烈磨损、磨合、稳定磨损B. 稳定磨损，剧烈磨损、磨合C. 磨合、剧烈磨损、稳定磨损D. 磨合、稳定磨损、剧烈磨损2、设计斜齿圆柱齿轮传动时，螺旋角β一般在80～200范围内选取，β太小斜齿轮传动的优点不明显，太大则会引起( B )。

A. 大的切向力B. 大的轴向力C. 小的切向力D. 小的轴向力3、若一滚动轴承的寿命为1370000转，则该轴承所承受的当量动载荷( B )基本额定动载荷。

A. 等于B. 小于C. 大于D. 无法判断4、在不完全液体润滑滑动轴承设计中，除了限制轴承p值外，还要对轴承pv值进行验算，其主要目的是( B )。

A. 限制轴承过渡磨损B. 限制轴承的温升C. 保证轴承的强度D. 限制轴承的质量5、通常，一部机器主要是由( A )三部分构成的。

A. 原动部分，传动部分，执行部分B. 原动部分，传动部分，控制部分C. 辅助系统，传动部分，控制部分D. 原动部分，控制部分，执行部分6、一般参数的闭式硬齿面齿轮传动的主要失效形式是( B )。

A.齿面点蚀B.轮齿折断C.齿面磨粒磨损D.齿面胶合7、在V 带传动中，小轮包角一般应大于( D )度。

A. 90︒B. 100︒C. 150︒D.120︒8、一齿轮传动，主动轮1用45号钢调质，从动轮2用45号钢正火，则它们的齿面接触应力( C )。

A. 12H H σσ>B. 12H H σσ<C. 12H H σσ=D. 无法判断9、蜗杆蜗轮传动的传动比，正确表达式是( B )。

A. 21d i d = B. 21z i z = C. 21n i n = D. 12d i d = 10、设计一对材料相同的软齿面齿轮传动时，一般应使大齿轮的齿面硬度2HBS ( B )小齿轮的齿面硬度1HBS 。

A. 大于B. 小于C. 等于D. 大于或等于二、填空题(共10分)1、在轴的结构设计中，轴的最小直径d min 是按 轴的扭矩 初步确定的。