两点边值问题的有限差分法
- 格式:doc
- 大小:219.00 KB
- 文档页数:9

分数阶微分方程两点边值问题正解的存在性如何理解分数阶微分方程两点边值问题正解的存在性正解,正解是指题目的正确答案或者正确的解决方案,通常用于测验、考试等场景。
正解边值问题,最小边值问题(Minimum Cut Problem)指在一个连通的加权图G(V,E)中找到一个切割S,使得S中包含的边的总权重最小。
G表示一个有向图或无向图,V代表其节点集合,E表示其边集合,边e的权重用w(e)表示。
S是V的子集合,S-S表示S的补集,切割S定义为从V到S-S的路径中的边的集合。
要得到最小的切割,我们就要求出最小的边权重和。
正解边值问题微分方程,边值问题微分方程定义是指一类常微分方程,给出了在某个区间的未知函数及其一阶导数的某些边界条件,要求求出该函数在这个区间内的解。
正解边值问题微分方程分数,式为:∂u/∂t + a∂u/∂x = b(∂²u/∂x²) + c(∂u/∂x)其中,u是函数的值,a、b、c是常量参数。
其中:∂u/∂t表示函数u随时间的变化率;∂u/∂x表示函数u随空间的变化率;∂²u/∂x²表示函数u随空间的二阶变化率。
分数阶微分方程两点边值问题正解的存在性,答:一阶分数阶微分方程两点边值问题的正解存在性取决于给定边值问题的可解性。
一般来说,当方程有足够的初值解的连续性或足够的连续性以及给定的两点边值条件,正解就存在。
为什么需要分数阶微分方程两点边值问题正解的存在性1.意义意味着当各种不同的初始/边界条件及其未知函数给定时,它能找到合适的解决方法。
2.它说明了求解此问题的算法的可靠性,从而保证了其精确性和有效性。
3.它能帮助科学家和工程师更好地了解其实际应用中出现的一系列问题的原因和解决方案,从而可以更有效地解决问题。
怎么进一步推进完成分数阶微分方程两点边值问题正解的存在性1. 利用Kirchhoff积分变换,尝试将微分方程转化为微分不等式来证明有限解的存在性。

PDE 数值计算的有限差分法《图像处理的PDE 方法》对给定的PDE 往往很难求其解析解,尤其是在实际问题中,这就需要求助于数值计算以获取该问题的近似解,常用的PDE 数值方法有有限差分法、有限元法和谱法等,其中,有限差分法应用得最为广泛。
因为待处理的图像通常已经是在二维空间中,按等采样而得到的离散化数字图像,这就自然构成了有限差分法所需要的等分网格(Grid )。
1、有限差分格式有限差分的基本思想是:利用相距有限距离的两邻点的函数值的差与两点间距离的比值来近似函数对变量的偏导数。
例如,用向前差分来近似对时间的偏导数tu ∂∂,即n it nin iniuD tu u tu )(1++=∆-=∂∂对于空间中的一阶偏导数,除上面的向前差分外,还有向后差分、中心差分等,如下:向前差分:n ix nin i niuD tu u xu )(1++=∆-=∂∂后向差分:n ix ni n i niuD xu u xu )(1--=∆-=∂∂中心差分:n ix ni n i niuD xu u xu )0(112=∆-=∂∂-+根据泰勒展开式,有()+∆∂∂+∆∂∂+=∆+22221)()(x xu x xu x u x x u因此可得)()()(x O xx u x x u xu ∆+∆-∆+=∂∂说明向前差分和向后差分是一阶精度的。
同时,由于()+∆∂∂+∆∂∂+=∆+22221)()(x xu x x u x u x x u ()+∆∂∂+∆∂∂-=∆-22221)()(x xu x xu x u x x u可得())(2)()(2x O xx x u x x u xu ∆+∆∆--∆+=∂∂说明中心差分是二阶精度的。
当偏微分议程中含有二阶偏导数时,同样采用有限差分进行处理,先求出两个半点处的一阶偏导数中心差分,如下:x u u x u ni ni ni ∆-=⎥⎦⎤⎢⎣⎡∂∂++12/1,x u u x u ni n ini ∆-=⎥⎦⎤⎢⎣⎡∂∂--12/1然后再利用这两个一阶差分,作一次中心差分,得:()n ixx ni n i n i ni n i niuD x u u u xx u x u x u )0(2112/12/1222=∆+-=∆⎥⎦⎤⎢⎣⎡∂∂-⎥⎦⎤⎢⎣⎡∂∂=⎥⎦⎤⎢⎣⎡∂∂-+-+对于二阶偏导数yx u ∂∂∂2,同样采用类似的方法来处理,如下:x u u u u x u u x u j i j i j i j i j i j i j i ∆--+=∆-=⎥⎦⎤⎢⎣⎡∂∂+--++++-+++421,1,11,1,12/1,12/1,12/1,x u u u u x u u x u j i j i j i j i j i j i j i ∆--+=∆-=⎥⎦⎤⎢⎣⎡∂∂---+-+---+-42,11,1,11,12/1,12/1,12/1,其中()1,1,12/1,121++++++=j i ji j i u u u ()1,1,12/1,121+--+-+=j i ji j i u u u ()j i j i j i u u u ,11,12/1,121+-+-++= ()j i j i j i u uu ,11,12/1,121-----+=因此,yx u u u u yx u u u u u u u u yx u u u u yx u u u u yx u x u y x u j i j i j i j i ji j i j i j i j i j i j i j i ji j i j i j i j i j i j i j i j i j i nj i ∆∆--+=∆∆----+++=∆∆--+-∆∆--+=∆⎥⎦⎤⎢⎣⎡∂∂-⎥⎦⎤⎢⎣⎡∂∂=⎥⎦⎤⎢⎣⎡∂∂∂-++---+++-++-----+++---+-++--+++-+44441,11,11,11,1,11,11,1,1,11,11,1,1,11,1,11,11,1,11,1,12/1,2/1,,22、显式、隐式和半隐式方案以一维Burgers 方程xu ut u ∂∂=∂∂来说明几种PDE 的数值计算方案。

有限差分法理解知乎
有限差分法是一种常用的数值计算方法,广泛应用于解决偏微分方程等数学问题。
它的基本思想是将连续的数学问题转化为离散的数值问题,然后通过计算机进行求解。
所谓差分法,即是将连续变量的微分近似转化为离散变量的差分,从而通过数值计算得到近似解。
在有限差分法中,我们将求解区域划分为有限个网格点,然后通过近似求解这些网格点上的差分方程,从而得到整个区域上的近似解。
有限差分法的基本步骤包括以下几个方面:首先,将求解区域进行离散化划分,形成网格;然后,在网格点上建立差分方程,根据问题的特点和所需精度选择差分格式;接着,根据差分方程,将待求解的变量表达为已知量的函数,并组成一系列代数方程;最后,利用数值计算方法,求解这些代数方程,得到所要的数值解。
有限差分法的优点是简单易行,计算效率高,可以用于各种类型的偏微分方程的求解。
然而,也存在一些限制和注意事项,例如需要合理选择网格划分和差分格式,以及应对边界条件的处理等。
总的来说,有限差分法是一种重要的数值计算方法,它通过将连续问题离散化为离散问题,利用数值计算求解这些问题,从而得到近似解。
在实际应用中,有限差分法具有广泛的应用价值,可以解决各种科学工程中的数学问题。



一、有限差分法的原理与计算步骤
1.原理
基本思想是把连续的定解区域用有限个离散点构成的网格来代替,这些离散点称作网格的节点;把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似;把原方程和定解条件中的微商用差商来近似,积分用积分和来近似,于是原微分方程和定解条件就近似地代之以代数方程组,即有限差分方程组,解此方程组就可以得到原问题在离散点上的近似解。
然后再利用插值方法便可以从离散解得到定解问题在整个区域上的近似解。
2. 计算步骤
在采用数值计算方法求解偏微分方程时,若将每一处导数由有限差分近似公式替代,从而把求解偏微分方程的问题转换成求解代数方程的问题,即所谓的有限差分法。
有限差分法求解偏微分方程的步骤如下:
(1)区域离散化,即把所给偏微分方程的求解区域细分成由有限个格点组成的网格;
(2)近似替代,即采用有限差分公式替代每一个格点的导数;
(3)逼近求解。
换而言之,这一过程可以看作是用一个插值多项式及其微分来代替偏微分方程的解的过程
二、有限差分法的程序流程图。

学生实验报告实验课程名称偏微分方程数值解开课实验室数统学院学院数统年级2021专业班信计2班学生姓名学号开课时间2021 至2021学年第2学期数学与统计学院制开课学院、实验室:数统学院实验时间:2021年月日1,...,1i N =-,网点处准确解记为[]i u ,1,...,1i N =-。
然后计算相应的误差[]0max Ni i ci Ne u u <<=-,[]121N Ni i i e h u u -==-∑及收敛阶()2ln ln 2NNe e ,将计算结果填入第五局部的表格,并对表格中的结果进展解释?4. 将数值解和准确解画图显示,每种网格上的解画在一图。
三.实验原理、方法〔算法〕、步骤1. 差分格式:=-1/h^2(-()+)+()/2h+=A,2. 局部阶段误差: (u)=O(h^2)3.程序clear allN=10; a=0;b=1;p=(x) 1; r=(x) 2; q=(x) 3; alpha=0;beta=1;五.实验结果及实例分析NN ce收敛阶N e收敛阶10 0.00104256 …… 0.00073524 …… 20 0.00026168 1.9341 0.00018348 1.4530 40 0.00006541 2.0001 0.00004585 2.0000 80 0.00001636 1.9993 0.00001146 2.0000 1600.000004092.00000.000002872.0000N 越大 只会使绝对误差变小,方法没变,所以收敛阶一致。
图示为:(绿线为解析解,蓝线为计算解)N=10N=20N=40N=80N=160。

有限差分法边界条件
《有限差分法边界条件》
嘿呀,今天咱来聊聊这个有限差分法边界条件。
就好像我那次去海边玩一样,这有限差分法边界条件就像是海边的边界。
你想啊,海水有它流动的范围吧,那岸边就是它的一个边界。
而有限差分法边界条件呢,也是给计算划定了一个范围。
就像在海边,我们知道不能超出那个岸边,不然就掉海里啦。
比如说在计算的时候,我们要确定一些边界上的数值,这就好比在海边我们要知道哪里是安全的,哪里不能再往前走了。
如果边界条件没搞清楚,那计算就可能出大乱子,就像在海边不小心走到深水区,那可就危险咯。
我记得那次在海边,我沿着沙滩走啊走,一直走到一个礁石那里,那礁石就像是一个明确的边界。
我不能再往前了,得绕过去或者停下来。
这和有限差分法边界条件是一个道理呀,到了特定的边界,就得按照规则来处理。
而且这边界条件还分不同类型呢,就像海边有不同的地形一样。
有的边界可能是固定的,就像坚固的悬崖;有的边界可能是变化的,就像海浪不断拍打的地方。
咱在研究有限差分法边界条件的时候,也得像在海边探索一样小心翼翼。
要把每个边界都搞清楚,不然就可能在计算的海洋里迷失方向啦。
总之呢,有限差分法边界条件虽然听起来有点专业有点复杂,但其实就和我们生活中的很多边界一样。
就像那次海边之旅让我明白边界的重要性,研究有限差分法边界条件也是为了让我们的计算更准确、更可靠呀。
下次再看到有限差分法边界条件,就想想那片广阔的大海和海边的边界吧,哈哈!。

本科毕业设计常熟理工学院本科毕业设计(论文)诚信承诺书本人郑重声明:所呈交的本科毕业设计(论文),是本人在导师的指导下,独立进行研究工作所取得的成果。
除文中已经注明引用的内容外,本论文不含任何其他个人或集体已经发表或撰写过的作品成果。
对本文的研究做出重要贡献的个人和集体,均已在文中以明确方式标明。
本人完全意识到本声明的法律结果由本人承担。
本人签名:日期:常熟理工学院本科毕业设计(论文)使用授权说明本人完全了解常熟理工学院有关收集、保留和使用毕业设计(论文)的规定,即:本科生在校期间进行毕业设计(论文)工作的知识产权单位属常熟理工学院。
学校有权保留并向国家有关部门或机构送交论文的复印件和电子版,允许毕业设计(论文)被查阅和借阅;学校可以将毕业设计(论文)的全部或部分内容编入有关数据库进行检索,可以采用影印、缩印或扫描等复制手段保存、汇编毕业设计(论文),并且本人电子文档和纸质论文的内容相一致。
保密的毕业设计(论文)在解密后遵守此规定。
本人签名:日期:导师签名:日期:泰勒公式在二阶两点边值问题求解方法上的应用摘要本文主要讨论利用泰勒展开公式求解二阶线性常微分方程问题. 首先介绍泰勒公式的相关知识;其次,基于泰勒展开公式,提出一种求解线性二阶线性常微分方程问题初值问题的新方法;然后,通过结合提出的求解线性二阶线性常微分方程问题初值问题的方法和打靶方法, 提出一种求解线性二阶线性常微分方程问题边值问题的数值方法;最后通过数值算例来验证所提数值方法的有效性.关键词:泰勒展开式二阶线性常微分方程两点边值问题近似解Taylor formula in the second order two-point boundary value problemsolving the application of the methodAbstractThis thesis mainly discusses numerical methods for solving second order linear ordinary differential equations by using Taylor's expansion formula. Firstly, some theory of Taylor's expansion formula is introduced. Secondly, a numerical method for solving second order linear initial value problems is proposed. Thirdly, a numerical method for solving second order linear two-point boundary value problems is developed by combining the method for initial value problems and shooting method. Finally, numerical examples are provided to show the validity of the present methods.Key Words: Taylor's expansion; Second order linear ordinary differential equations; Two–point boundary value problems; Approximate solution目录1. 引言 (1)1.1微分方程边值问题的介绍 (1)1.2 二阶两点边值问题的介绍 (2)2. 泰勒公式简介 (4)2.1泰勒公式简介 (4)2.2泰勒公式的应用 (5)3.二阶线性初值问题 (7)3.1求解方法 (7)3.2数值算例 (8)4.二阶线性两点边值问题的求解方法 (10)4.1求解方法 (10)4.2数值算例 (11)结语 (13)参考文献 (14)致谢 (15)1 引言1.1微分方程边值问题的介绍微分方程是现代数学中的一个很重要的分支,从早期的微积分时代起,这个学科就成为了理论研究和实践应用的一个重要领域。
数值方法13——两点边值问题
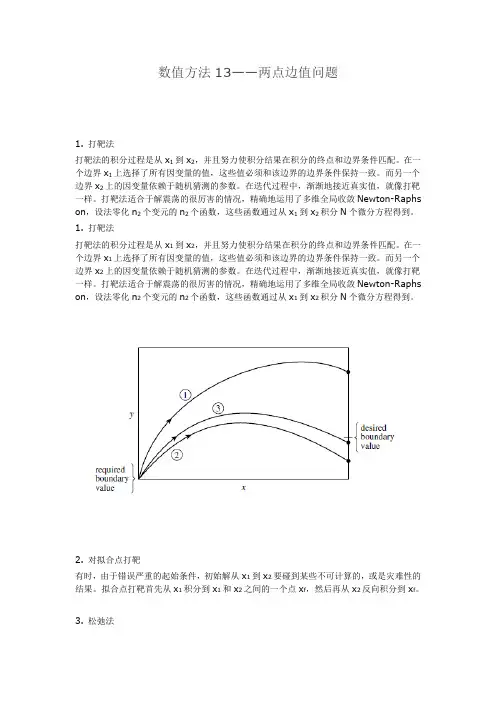
1. 打靶法
打靶法的积分过程是从x1到x2,并且努力使积分结果在积分的终点和边界条件匹配。
在一个边界x1上选择了所有因变量的值,这些值必须和该边界的边界条件保持一致。
而另一个边界x2上的因变量依赖于随机猜测的参数。
在迭代过程中,渐渐地接近真实值,就像打靶一样。
打靶法适合于解震荡的很厉害的情况,精确地运用了多维全局收敛Newton-Raphs on,设法零化n2个变元的n2个函数,这些函数通过从x1到x2积分N个微分方程得到。
1. 打靶法
打靶法的积分过程是从x1到x2,并且努力使积分结果在积分的终点和边界条件匹配。
在一个边界x1上选择了所有因变量的值,这些值必须和该边界的边界条件保持一致。
而另一个边界x2上的因变量依赖于随机猜测的参数。
在迭代过程中,渐渐地接近真实值,就像打靶一样。
打靶法适合于解震荡的很厉害的情况,精确地运用了多维全局收敛Newton-Raphs on,设法零化n2个变元的n2个函数,这些函数通过从x1到x2积分N个微分方程得到。
2. 对拟合点打靶
有时,由于错误严重的起始条件,初始解从x1到x2要碰到某些不可计算的,或是灾难性的结果。
拟合点打靶首先从x1积分到x1和x2之间的一个点x f,然后再从x2反向积分到x f。
3. 松弛法
松弛法用了另外一种逼近方法,微分方程由覆盖积分限的一系列有限个差分方程来替代,试验解由各个网格点上的因变量的值组成,并不满足所需的有限个差分方程和边界条件。
迭代调整所有在网格上的值,使他们满足各个联系的差分方程,也满足边界条件。
适用于解平滑的情况,需要良好的初始预测值。
两点边值问题的解法
两点边值问题是数学中常遇到的问题,其解法有很多种,下面是其中一种常见的解法:
1. 分离变量法:将微分方程中的变量分离出来,得到一个只含有一个变量的微分方程,然后求解这个微分方程,得到通解。
2. 特征方程法:对于一些特定类型的微分方程,可以通过求解特征方程来得到通解。
3. 积分因子法:通过引入积分因子,将微分方程转化为一个全微分方程,然后求解这个全微分方程,得到通解。
4. 数值解法:对于一些复杂的微分方程,无法得到解析解,可以使用数值方法来求解,例如有限差分法、有限元法等。
以上是常见的两点边值问题的解法,具体的解法需要根据具体的问题来选择。
在实际应用中,需要根据问题的特点和要求选择合适的解法。
有限差分法施加边界条件说起有限差分法,你可能会想:“哎,这个又是什么东东?跟我有什么关系?”别急,慢慢听我给你讲。
在我们研究物理问题或者做一些数学建模的时候,总是会遇到很多需要用到数值方法的情况,比如说解一些微分方程。
这时候,有限差分法就是咱们的好帮手。
别小看它,虽然名字有点生涩,但实际上它就像你天天用的计算器一样,简简单单,一点儿也不复杂。
说白了,有限差分法就是把问题从“无穷”变成了“有限”,把数学方程变得易于解决。
它把无限的小变化切成了一个个有限的片段,让我们能够轻松搞定。
不过呢,说到有限差分法,你肯定得面对一个小小的麻烦——边界条件。
你瞧,这个边界条件就像是你玩游戏时的“通关任务”。
没搞定边界条件,后面的事情根本没法继续。
尤其是在解决一些热传导问题、电场问题,或者流体力学问题时,边界条件就显得尤为重要。
想象一下,如果你不知道物体的边界是什么,怎么知道热量从哪儿进,流体从哪儿流呢?不行,没办法继续。
就好像你做饭的时候,锅底得有水,才能开始煮,不然锅就干烧了,别提多麻烦。
我们的物理问题边界条件很明确,比如说,物体两端的温度已经定好了,或者两端的速度已经给定了。
这个时候,咱们就直接按照给定的条件来做。
嘿,简单吧?不过问题是,很多时候这些边界条件根本不是那么“明白”地给出来。
就像你上学时,考试卷子上有些题目,明明你会做,但它给的条件有点模糊,让你不知从何下手。
这时候,有限差分法就得给我们提供一个“接地气”的办法,让我们能够合理地假设、设定边界条件。
比如,如果你做热传导问题,可能有时候热量流动的边界是固定的,比如某个位置温度不变。
这个时候,有限差分法就是通过把整个计算区域分成小块,每一块的值都跟相邻的块儿的值有关系。
在这个过程当中,咱们通过给定“边界”的温度或者热量值来“控制”这些小块儿的计算,保证计算结果跟实际物理情况相符。
就是这种“点到点”的联系,让整个问题不再晦涩难懂。
但你要是没有边界条件,或者说边界条件不那么直接,就得用一些“假设”来推导。
有限差分法求解步骤嘿,朋友们!今天咱就来聊聊这个有限差分法求解步骤。
这玩意儿啊,就像是搭积木,一块一块地来,最后就能搭出个漂亮的“城堡”。
咱先得搞清楚问题是啥,就像要知道咱要搭个啥样的积木城堡。
然后呢,把这个问题的区域划分成一个个小格子,这就好比把积木分成小块小块的。
接下来可就关键啦!要确定这些小格子之间的关系,就像知道每个积木块怎么连接在一起。
这一步可得细心,不能马虎,不然“城堡”可就歪歪扭扭啦。
然后呢,根据已知条件,给这些小格子填上合适的值,这就像给积木涂上颜色,让它更漂亮。
再之后啊,用各种公式和算法,在这些小格子之间来回计算,就像让积木们手牵手,一起组成城堡的形状。
这计算的过程可不能着急,得慢慢来,就像搭积木不能一下子堆上去,得一层一层稳稳当当的。
有时候可能会遇到难题,哎呀,这可咋办呢?别着急,咱就静下心来,好好琢磨琢磨,肯定能找到解决办法的。
等算出结果啦,咱还得检查检查,看看对不对,就像搭完积木城堡后要看看有没有哪里不牢固。
要是有问题,那就赶紧回头再算一遍,可不能马马虎虎就过去了。
你说这有限差分法求解步骤像不像一场有趣的冒险?每一步都充满了挑战和惊喜。
咱就像是勇敢的探险家,在数学的海洋里遨游,寻找那珍贵的答案。
你想想,要是咱能熟练掌握这有限差分法求解步骤,那以后遇到啥问题都不怕啦!咱就能像个大侠一样,轻松解决难题,多威风啊!所以啊,朋友们,可别小瞧了这看似复杂的步骤,只要咱用心去学,去钻研,肯定能掌握得牢牢的。
而且啊,这有限差分法在好多领域都能用得上呢!比如物理啦、工程啦等等。
学会了它,就像有了一把万能钥匙,能打开好多知识的大门呢!所以啊,大家都加油吧!让我们一起在有限差分法的世界里畅游,把那些难题都一个一个地攻克掉!怎么样,是不是觉得很有意思呀?赶紧行动起来吧!。
有限差分方法有限差分方法一种求偏微分(或常微分)方程和方程组定解问题的数值解的方法,简称差分方法。
微分方程的定解问题就是在满足某些定解条件下求微分方程的解。
在空间区域的边界上要满足的定解条件称为边值条件。
如果问题与时间有关,在初始时刻所要满足的定解条件,称为初值条件。
不含时间而只带边值条件的定解问题,称为边值问题。
与时间有关而只带初值条件的定解问题,称为初值问题。
同时带有两种定解条件的问题,称为初值边值混合问题。
定解问题往往不具有解析解,或者其解析解不易计算。
所以要采用可行的数值解法。
有限差分方法就是一种数值解法,它的基本思想是先把问题的定义域进行网格剖分,然后在网格点上,按适当的数值微分公式把定解问题中的微商换成差商,从而把原问题离散化为差分格式,进而求出数值解。
此外,还要研究差分格式的解的存在性和唯一性、解的求法、解法的数值稳定性、差分格式的解与原定解问题的真解的误差估计、差分格式的解当网格大小趋于零时是否趋于真解(即收敛性),等等。
有限差分方法具有简单、灵活以及通用性强等特点,容易在计算机上实现。
偏微分方程初值问题的差分法许多物理现象随着时间而发生变化、如热传导过程、气体扩散过程和波的传播过程都与时间有关。
描述这些过程的偏微分方程具有这样的性质:若初始时刻t=t0的解已给定,则t t0时刻的解完全取决于初始条件和某些边界条件。
利用差分法解这类问题,就是从初始值出发,通过差分格式沿时间增加的方向,逐步求出微分方程的近似解。
双曲型方程的差分方法最简单的双曲型方程的初值问题是:式中嫓(x)为已知初值函数。
这初值问题的解是:u(x,t)=嫓(x-at)。
(2)由(2)可见,(1a)(1b)的解(2)当a>0时代表一个以有限的速度a沿特征线x-at=常数向右传播的波,而解u(x,t)在P(慜,惭)点的值完全由嫓(x)在x轴上的点A(慜-а惭,0)的值决定。
A点就是双曲型方程(1a)在P点的依赖域(图1)。
学生实验报告
实验课程名称偏微分方程数值解
开课实验室数统学院
学院数统年级2013 专业班信计2班学生姓名学号
开课时间2015 至2016 学年第 2 学期
数学与统计学院制
开课学院、实验室:数统学院实验时间:2016年月日
[]0max N
i i c
i N
e
u u <<=-,[]1
2
1
N N
i
i
i e
h u u
-==
-∑及收敛阶
(
)2ln ln 2
N
N
e e ,将计算结果填入
第五部分的表格,并对表格中的结果进行解释?
4. 将数值解和精确解画图显示,每种网格上的解画在一张图。
三.实验原理、方法(算法)、步骤
1. 差分格式:
=-1/h^2(-(
)
+
)+
(
)/2h+
= A,
2. 局部阶段误差: (u)=O(h^2)
3.程序
clear all N=10; a=0;b=1;
p=@(x) 1; r=@(x) 2; q=@(x) 3; alpha=0;beta=1;
f=@(x) (4*x^2-2)*exp(x-1);
h=(b-a)/N;
H=zeros(N-1,N-1);g=zeros(N-1,1); % for i=1
H(i,i)=2*(p(a+(i+1/2)*h)+p(a+(i-1/2)*h))/h+2*h*q(a+i*h); H(i,i+1)=-(2*p(a+(i+1/2)*h)/h-r(a+i*h));
g(i)=2*h*f(a+i*h)+(2*p(a+(i-1/2)*h)/h+r(a+i*h))*alpha; end
五.实验结果及实例分析
N
N c
e
收敛阶
N e
收敛阶
10 0.00104256 …… 0.00073524 …… 20 0.00026168 1.9341 0.00018348 1.4530 40 0.00006541 2.0001 0.00004585 2.0000 80 0.00001636 1.9993 0.00001146 2.0000 160
0.00000409 2.0000
0.00000287
2.0000
N 越大 只会使绝对误差变小,方法没变,所以收敛阶一致。
图示为:(绿线为解析解,蓝线为计算解)
N=10
N=20
N=40 N=80
N=160。