Monte_Carlo方法必备知识

第八讲蒙特卡罗方法蒙特卡罗（Monte Carlo简称MC）方法又称随机抽样法（Random Sampling）、随机模拟（Random Simulation）或统计试验法(Statistic Testing）。

这个方法的起源可以追溯到十七世纪或更早的年代。

Monte Carlo 是摩纳哥（Monaco）的一个著名城市，位于地中海之滨，以旅游赌博闻名。

Von Neumann 等人把计算机随机模拟方法定名为Monte Carlo方法，显然反映了这种方法带有随机的性质。

简单地说，MC方法是一种利用随机统计规律，进行计算和模拟的方法。

它可用于数值计算，也可用于数字仿真。

在数值计算方面，可用于多重积分、线性代数求解、矩阵求逆以及用于方程求解，包括常微分方程、偏微分方程、本征方程、非齐次线性积分方程和非线性方程等。

在数字仿真方面，常用于核系统临界条件模拟、反应堆模拟以及实验核物理、高能物理、统计物理、真空、地震、生物物理和信息物理等领域。

§8.l蒙特卡罗方法的基础知识8.1.1 基本概念为了对MC方法有一点初步的认识，请先看使用MC方法的几个例子。

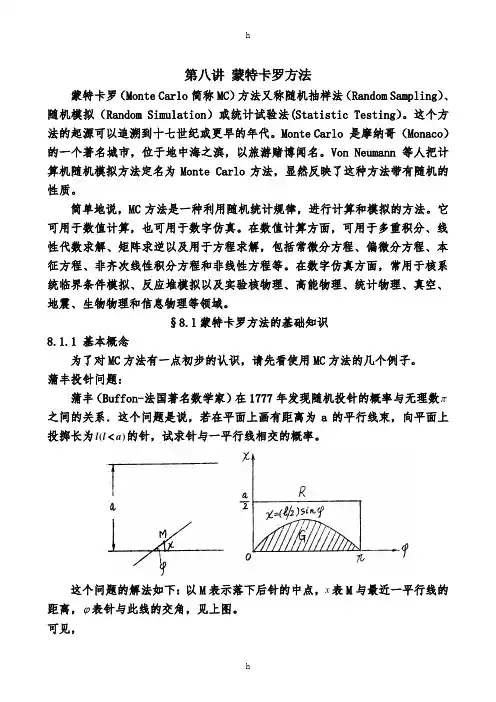
蒲丰投针问题：蒲丰（Buffon-法国著名数学家）在1777年发现随机投针的概率与无理数π之间的关系．这个问题是说，若在平面上画有距离为a的平行线束，向平面上投掷长为()<的针，试求针与一平行线相交的概率。

l l a这个问题的解法如下：以M表示落下后针的中点，x表M与最近一平行线的距离，ϕ表针与此线的交角，见上图。

可见，02 0≤≤≤≤/,x a ϕπ这两式决定x ϕ平面上一矩形R ；为了使针与一平行线（这线必定是与针中点M 最近的平行线）相交，充分而且必要条件是2ϕ≤sin lx 这个不等式决定R 中一个子集G 。

因此，我们的问题等价于向R 中均匀分布地掷点而求点落于G 中的概率P.根据概率的几何意义，得222sin ()ld l P a a πϕϕππ==⎰此式提供了求π值的一个方法：可以通过投针事件求得针与平行线相交概率P ，求得π值：2/()l Pa π= （8.1）若投掷次数为m ，针与平行线相交的次数为n ，那么/p n m ≈即 2/()lm an π≈于是，可用投针试验来求无理数π的近似值．下表列举了历史上若干学者投针试验计算π值的结果：射击问题（打靶游戏）：设r 表示射击运动员的弹着点到靶心的距离，()g r 表示击中r 处相应的得分数（环数），分布密度函数()f r 表示该运动员的弹着点分布，它反映运动员射击水平。

蒙特卡洛法的基本原理蒙特卡洛法（Monte Carlo method）是一种基于随机抽样的数值计算方法，用于解决难以通过解析方法或传统数学模型求解的问题。

它在物理学、化学、工程学、计算机科学、金融学、生物学等领域都有广泛应用。

本文将介绍蒙特卡洛法的基本原理，包括随机数生成、统计抽样、蒙特卡洛积分、随机漫步等方面。

一、随机数生成随机数是蒙特卡洛法中的基本元素，其质量直接影响着计算结果的准确性。

随机数的生成必须具有一定的随机性和均匀性。

常见的随机数生成方法有：线性同余法、拉斯维加斯法、梅森旋转算法、反序列化等。

梅森旋转算法是一种广泛使用的准随机数生成方法，其随机数序列的周期性长、随机性好，可以满足大多数应用的需要。

二、统计抽样蒙特卡洛法利用抽样的思想，通过对输入参数进行随机取样，来模拟整个系统的行为，并推断出某个问题的答案。

统计抽样是蒙特卡洛方法中最核心的部分，是通过对概率分布进行样本抽取来模拟随机事件的发生，从而得到数值计算的结果。

常用的统计抽样方法有：均匀分布抽样、正态分布抽样、指数分布抽样、泊松分布抽样等。

通过对这些概率分布进行抽样，可以在大量随机取样后得到一个概率分布近似于输入分布的“抽样分布”，进而求出所需的数值计算结果。

三、蒙特卡洛积分蒙特卡洛积分是蒙特卡洛法的重要应用之一。

它利用统计抽样的思想，通过对输入函数进行随机抽样，计算其随机取样后的平均值，来估算积分的值。

蒙特卡洛积分的计算精度与随机取样的数量、抽样分布的质量等因素有关。

蒙特卡洛积分的计算公式如下：$I=\frac{1}{N}\sum_{i=1}^{N}f(X_{i})\frac{V}{p(X_{i})}$$N$为随机取样的数量，$f(X_{i})$为输入函数在点$X_{i}$的取值，$V$为积分区域的体积，$p(X_{i})$为在点$X_{i}$出现的抽样分布的概率密度函数。

通过大量的样本拟合，可以估算出$I$的值接近于真实积分的值。

蒙特卡罗（Monte Carlo method）方法知识详解蒙特卡罗方法（英语：Monte Carlo method），也称统计模拟方法，是1940年代中期由于科学技术的发展和电子计算机的发明，而提出的一种以概率统计理论为指导的数值计算方法。

是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。

20世纪40年代，在冯·诺伊曼，斯塔尼斯拉夫·乌拉姆和尼古拉斯·梅特罗波利斯在洛斯阿拉莫斯国家实验室为核武器计划工作时，发明了蒙特卡罗方法。

因为乌拉姆的叔叔经常在摩纳哥的蒙特卡洛赌场输钱得名，而蒙特卡罗方法正是以概率为基础的方法。

与它对应的是确定性算法。

蒙特卡罗方法在金融工程学、宏观经济学、生物医学、计算物理学（如粒子输运计算、量子热力学计算、空气动力学计算）机器学习等领域应用广泛。

一、蒙特卡罗方法的基本思想通常蒙特卡罗方法可以粗略地分成两类：一类是所求解的问题本身具有内在的随机性，借助计算机的运算能力可以直接模拟这种随机的过程。

例如在核物理研究中，分析中子在反应堆中的传输过程。

中子与原子核作用受到量子力学规律的制约，人们只能知道它们相互作用发生的概率，却无法准确获得中子与原子核作用时的位置以及裂变产生的新中子的行进速率和方向。

科学家依据其概率进行随机抽样得到裂变位置、速度和方向，这样模拟大量中子的行为后，经过统计就能获得中子传输的范围，作为反应堆设计的依据。

另一种类型是所求解问题可以转化为某种随机分布的特征数，比如随机事件出现的概率，或者随机变量的期望值。

通过随机抽样的方法，以随机事件出现的频率估计其概率，或者以抽样的数字特征估算随机变量的数字特征，并将其作为问题的解。

这种方法多用于求解复杂的多维积分问题。

假设我们要计算一个不规则图形的面积，那么图形的不规则程度和分析性计算（比如，积分）的复杂程度是成正比的。

蒙特卡罗方法基于这样的思想：假想你有一袋豆子，把豆子均匀地朝这个图形上撒，然后数这个图形之中有多少颗豆子，这个豆子的数目就是图形的面积。

蒙特卡洛方法的基本概念与应用蒙特卡洛方法（Monte Carlo method）是一种基于随机取样的计算方法，通过大量的随机实验来近似计算数学问题。

它的基本思想是通过生成随机数来模拟实验过程，然后利用实验结果进行统计分析，从而得到所求解的数值。

一、蒙特卡洛方法的基本原理蒙特卡洛方法的基本原理是基于概率统计的思想，通过随机实验来获取近似计算结果。

其基本步骤如下：1. 建立数学模型：首先要确定问题的数学模型，即问题的数学表达式或方程。

2. 生成随机变量：通过随机数生成器生成服从特定分布的随机变量，这些随机变量将作为模型中的变量进行计算。

3. 执行实验模拟：根据模型和生成的随机变量，进行大量实验模拟并记录每次实验的结果。

4. 统计分析：对实验结果进行统计分析，如计算平均值、方差等。

5. 得出结论：利用统计分析的结果进行推断，得到问题的近似解。

二、蒙特卡洛方法的应用领域蒙特卡洛方法广泛应用于科学、工程、金融等领域，以解决大量变量和复杂概率分布下的问题。

以下是蒙特卡洛方法的一些应用场景：1. 金融领域：用于期权定价、风险度量和投资组合优化等问题。

例如，通过大量模拟实验可以计算期权的风险价值，从而评估期权的风险敞口。

2. 物理学领域：用于模拟粒子的轨迹、计算物理量等。

例如，在高能物理实验中，经常用蒙特卡洛方法来模拟粒子在探测器中的传输和相互作用过程。

3. 工程领域：用于模拟流体力学、应力分析等问题。

例如，在航空航天领域中，可以利用蒙特卡洛方法来计算飞机飞行过程中的结构应力。

4. 生物学领域：用于基因分析、蛋白质折叠等。

例如，在分子生物学中，可以通过蒙特卡洛方法来模拟蛋白质分子的折叠过程，以探索其结构和功能。

5. 计算机科学领域：用于算法优化、机器学习等问题。

例如，在优化算法中，可以利用蒙特卡洛方法来评估算法的性能，并选择最佳参数配置。

三、蒙特卡洛方法的优缺点蒙特卡洛方法具有以下优点：1. 灵活性：适用于各种复杂的问题，不受问题形式和维度的限制。

实验十二计算机仿真实验实验目的：1. 掌握全概率公式与贝叶斯公式；2. 了解计算机仿真方法；3. 了解蒙特卡罗法(Monte Carlo method), 具有初级编程能力.实验原理：全概率公式: 设A 1, A 2, …, A n 为两两互斥事件，B 是A 1 + A 2 + … + A n 的子事件，则P(B )=P(A 1)P(B |A 1) + P(A 2)P(B |A 2) + … + P(A n )P(B |A n ).贝叶斯公式: P(A k |B )= P(A k )P(B | A k )/P(B ).计算机仿真: 就是在计算机上模拟各种实际系统的运行过程. 计算机仿真通常用来产生规定分布的随机变量.对于任意随机变量ξ ，其分布函数为F (x )，设 η = F (ξ )的分布函数为G (y )，则G (y ) = P{η ≤y }= P{F (ξ ) ≤y }= P{ξ ≤F -1( y )}= y ，这说明η 服从[0，1]的均匀分布.一般的编程语言都提供了均匀分布随机数发生器.应用随机数模拟试验的方法通常称为蒙特卡罗法(Monte Carlo method). 蒙特卡罗法不仅适用于处理随机性问题, 如存贮、排队、质量检验、市场营销、社会救急、生态竞争和传染病等问题；也可处理定性问题, 如计算多重积分、解积分方程及微分方程、解整数规划(特别是非线性整数规划)等.应用蒙特卡罗法解规划问题的基本思想是：先估计各个变量的大致取值范围，每次试验从中随机取出一个样本点，然后判断它是否为可行点. 若是则将其目标函数值与上一次的目标函数值相比较，记录下较优目标函数值与其样本点；否则重新抽样。

直到试验次数达到指定值或可行点数达到指定值为止.实验内容：1. 设有两个口袋，甲袋中盛有两个白球，一个黑球，乙袋中盛有一个白球，两个黑球.由甲袋任取一个球放入乙袋，再从乙袋中取出一个球.若从乙袋中取出的球是白球，那么从甲袋中取出放入乙袋的球是白球还是黑球? 用计算机模拟上述过程1000次，问理论判断是正确的有多少次?2. 用计算机模拟随机变量ξ ～ϕ (x ) =⎩⎨⎧≤>-0,0,0,e 55x x 的取值200次. 3. 用计算机模拟随机变量ξ ～N (120,102 )的取值800次，并画出统计直方图.4. 应用蒙特卡罗法解非线性规划问题:max z = - 2x 2 - y 2 + xy + 8x + 3ys.t. 3 x + y = 10x ≥0, y ≥0.C 语言简介(仅介绍本实验所用到的)1.标识符标识符是由程序员定义的单词，如函数名、变量名等. 标识符是由大小写字母、数字和下划线组成的，并以字母和下划线开始.2.关键字void (无值型) char (字符型) int (整数型) long (长整数型) float (浮点型) double (双精度浮点型)if (如果) else (或者)for (循环) while (循环) break (满足一定的条件终止循环)return (返回函数值)3.函数形式类型函数名(参数){}4.库函数简介double sin(double x) double cos(double x) double exp(double x) double log(double x) double sqrt(double x) double pow(double x, double y)double fabs(double x) int abs(int x)int printf(const char *format, ...); 屏幕格式化输出函数FILE *fopen(const char *filename, const char *mode); 文件打开int fprintf(FILE *fp, const char *format, ...); 文件格式化输出函数int fgetc(FILE *fp); 从文件中读出一字符int fclose(FILE *fp); 文件关闭void far setcolor(int color); 设置输出颜色void far line(int x1, int y1, int x2, int y2); 画直线void far rectangle(int left, int top, int right, int bottom); 画矩形unsigned far getpixel(int x, int y); 读出点(x, y)的颜色void far putpixel(int x, int y, int pixelcolor); 画点int random(int Num), 均匀产生0到Num-1中的一个随机数5.示例计算9！#include<stdio.h>void main(void){int i;long n;n=1;for(i=1;i<=9;i++)n*=i;printf("\n9!=%ld\n",n);getch();}6. Turbo C(2.0) 编辑命令F3 录入文件F9 编译Ctrl+F9 运行Ctrl+KB 定义块首Ctrl+KK 定义块尾Ctrl+KC 块粘贴Ctrl+KV 块移动Ctrl+Y 删除当前行7.部分源程序程序LAB1_1.C 求出方程sin x- x = 1在( -2，2)内的近似根#include<stdio.h>#include<math.h>float f(float x){ return sin(x)-x-1; }void main(void){float r=0.618,x0=-2,x1=2,x;int n=0;while(1){n++;x=(1-r)*x0+r*x1;if(f(x)*f(x0)<0.0)x1=x;else if(f(x)*f(x1)<0.0)x0=x;else break;if(fabs(x1-x0)<0.001)break;}printf("n=%d, x=%f\n",n,x);getch();}程序LAB2_3.C 给出正态分布函数表#include<stdio.h>#include<math.h>float f(float x){ return exp(-x*x/2); }void main(void){float x,x0,x1=0.0,F=0,h=0.0001;long n=0;FILE *fp;int i=0,p;fp=fopen("x.c","w");for(x1=0.0;x1<0.04;x1+=0.001){n=0; F=0; x0=-10;for(x=x0+h;x<x1;x+=h){if(n%2)F+=2*f(x);else F+=4*f(x);n++;}F+=f(x0)+f(x1);F/=3; F*=h; F*=0.39894;printf("x=%5.3f, F=%6.4f\n",x1,F);i++;p=F*10000;fprintf(fp,"%d,",p);if(i==10){i=0;fprintf(fp,"\n ");}if(p==9999)break;}fclose(fp);getch();}程序LAB3_2_1.C 解下列微分方程y - y tan x = sec x ，y (0) = 0, 并画出其图形: #include <stdio.h>#include <math.h>#include <graphics.h>float f(float x,float y){ return y*sin(x)/cos(x)+1/cos(x); }void main(void){int i=DETECT,j;float x=0.0,y=0.0,h=0.005;char *str="0.00";initgraph(&i,&j," ");setviewport(0,0,639,479,1);cleardevice();setbkcolor(BLUE);setcolor(WHITE);line(20,200,620,200);for(i=0;i<10;i++){line(20+i*60,195,20+i*60,200);str[0]=48+3*i/10;str[2]=48+3*i%10;outtextxy(20+i*60,205,str);}for(i=0;i<600;i++){y=y+f(x,y)*h;x+=h;putpixel(i+20,200-y*10,GREEN);}getch();closegraph();}程序LAB3_2_2.C 解下列微分方程组⎪⎪⎩⎪⎪⎨⎧+-=-=.01.0d d ,25.02d d xy y t y xy x t x x (0) = 100, y (0) = 8, 并画出其图形:#include <stdio.h>#include <math.h>#include <graphics.h>float f1(float x,float y){ return 2*x-0.25*x*y; }float f2(float x,float y){ return -y+0.01*x*y; }void main(void){int i=DETECT,j;float x=99.0,y=7.9,h=0.015;initgraph(&i,&j," ");setviewport(0,0,639,479,1);cleardevice();for(i=0;i<600;i++){x=x+f1(x,y)*h;y=y+f2(x,y)*h;putpixel(i+20,(102.5-x)*60,GREEN);putpixel(i+20,(8.6-y)*600,WHITE);}getch();closegraph();}程序LAB4.C 将矩阵化为行阶梯型,化为行最简型#include<stdio.h>#include<math.h>#define MAXR 20#define MAXC 40/*解线性方程组,以下是其增广矩阵*/float M_B[MAXR][MAXC]={{1,-2,2,1,-3},{2,1,1,-2,-1},{3,4,0,-5,1}}; void f1(int m,int n){int i,j,r=0,c=0;float x0;printf("\n以下将矩阵化为行阶梯型\n");for(i=0;i<m;i++){for(j=0;j<n;j++)printf("%8.2f",M_B[i][j]);printf("\n");}printf("按任一健继续...\n");getch();while(c<n){for(i=r;i<m;i++)if(fabs(M_B[i][c])>=0.0001)break;if(i<m){if(i!=r)for(j=0;j<n;j++){x0=M_B[i][j];M_B[i][j]=M_B[r][j];M_B[r][j]=x0;}x0=M_B[r][c];for(j=0;j<n;j++)M_B[r][j]/=x0;for(i=r+1;i<m;i++){x0=M_B[i][c];for(j=0;j<n;j++)M_B[i][j]-=x0*M_B[r][j];}r++;for(i=0;i<m;i++){for(j=0;j<n;j++)printf("%8.2f",M_B[i][j]);printf("\n");}printf("按任一健继续...\n");getch();}c++;if(r==m)break;}printf("\n以下将行阶梯型化为行最简型\n");while(r){r--;for(j=0;j<n-1;j++)if(fabs(M_B[r][j])>=0.0001)break; c=j;for(i=0;i<r;i++){x0=M_B[i][c];for(j=0;j<n;j++)M_B[i][j]-=x0*M_B[r][j];}for(i=0;i<m;i++){for(j=0;j<n;j++)printf("%8.2f",M_B[i][j]);printf("\n");}printf("按任一健继续...\n");getch();}printf("完毕,按任一健退出...\n");getch();}void f2(int n){int i,j;for(i=0;i<n;i++)for(j=0;j<n;j++){if(i!=j)M_B[i][n+j]=0;else M_B[i][n+j]=1;}f1(n,2*n);}void main(void){ f1(3,5); }程序LAB6_3.C 模拟产生服从N(120,400)分布的随机变量800次,并画出统计直方图#include <stdio.h>#include <stdlib.h>#include <math.h>#include <graphics.h>int Np[4000]={/*下列数据为标准正态分布函数值×10000, 由程序LAB2_3.C 产生*/ 5000,5003,5007,5011,5015,5019,5023,5027,5031,5035,…};int f(int p){int i;for(i=0;i<4000;i++)if(Np[i]>=p)break;return i;}void main(void){int i,j,x;float F,X[800];randomize();printf("\n\n");for(i=0;i<800;i++){x=random(10000);if(x<5000)F=-f(10000-x);else F=f(x);F*=0.001;X[i]=120+20*F;printf("%8.2f",X[i]);}getch();i=DETECT;initgraph(&i,&j," ");setviewport(0,0,639,479,1);cleardevice();setbkcolor(BLUE);setcolor(WHITE);line(20,400,620,400);j=20;for(F=90;F<150;F+=3){x=0;for(i=0;i<800;i++)if(X[i]>=F&&X[i]<F+5)x+=4;rectangle(j,400-x,j+30,400);j+=30;}getch();closegraph();}程序2000A01.C 统计文件2000A1.txt中A TCG的个数#include<stdio.h>void main(void){int n=-1,ATCG[40][4]={0,0};char c;FILE *fp;fp=fopen("2000A1.txt","r");while((c=fgetc(fp))!=EOF){if(c=='.')n;else if(c=='a')ATCG[n][0];else if(c=='t')ATCG[n][1];else if(c=='c')ATCG[n][2];else if(c=='g')ATCG[n][3];}fclose(fp);for(n=0;n<40;n)printf("{%d,%d,%d,%d},\n",ATCG[n][0], ATCG[n][1],ATCG[n][2],ATCG[n][3]);getch();}。

蒙特卡洛方法是一种基于随机抽样的数值计算方法，广泛应用于金融学、物理学、工程学和计算机科学等领域。

它的原理是通过随机抽样来估计数学模型的结果，通过大量重复实验来逼近真实值。

在本文中，我们将探讨蒙特卡洛方法的原理、应用和局限，并共享个人对这一方法的理解和观点。

1. 蒙特卡洛方法的原理蒙特卡洛方法的核心思想是利用随机数来处理问题。

它通过生成大量的随机数，利用这些随机数的统计特性来近似求解问题。

在金融衍生品定价中，我们可以使用蒙特卡洛方法来模拟股票价格的随机漫步，从而估计期权合约的价格。

通过不断模拟股票价格的变化，并计算期权合约的价值，最终得到一个接近真实值的结果。

2. 蒙特卡洛方法的应用蒙特卡洛方法在金融领域被广泛应用于期权定价、风险管理和投资组合优化等问题。

在物理学中，蒙特卡洛方法可以用于模拟粒子的运动，求解无法用解析方法求解的复杂系统。

在工程学和计算机科学中，蒙特卡洛方法可以用于求解概率分布、优化问题和模拟系统行为。

3. 蒙特卡洛方法的局限虽然蒙特卡洛方法有着广泛的应用，但也存在一些局限性。

蒙特卡洛方法通常需要大量的随机抽样，计算成本较高。

随机性导致了结果的不确定性，需要进行大量的实验才能得到可靠的结果。

蒙特卡洛方法在高维问题和高精度要求下计算效率低下，需要借助其他数值方法进行辅助。

4. 个人观点和理解个人认为蒙特卡洛方法是一种非常强大的数值计算方法，能够解决复杂问题和高维问题。

它的随机性使得结果更加贴近真实情况，有利于处理实际情况中的不确定性和风险。

但是在实际应用中，需要注意随机抽样的方法和计算成本，并且需要结合其他数值方法进行验证和辅助，以确保结果的准确性和可靠性。

总结回顾蒙特卡洛方法是一种基于随机抽样的数值计算方法，通过大量重复实验来逼近真实值。

它在金融学、物理学、工程学和计算机科学等领域有着广泛的应用。

然而，蒙特卡洛方法也存在一些局限性，需要结合其他数值方法来弥补其不足。

个人认为蒙特卡洛方法是一种强大的数值计算方法，能够处理复杂和高维问题，但在实际应用中需要注意其随机性和计算成本。

（完整版）蒙特卡洛算法详讲Monte Carlo 法§8.1 概述Monte Carlo 法不同于前⾯⼏章所介绍的确定性数值⽅法，它是⽤来解决数学和物理问题的⾮确定性的（概率统计的或随机的）数值⽅法。

Monte Carlo ⽅法（MCM ），也称为统计试验⽅法，是理论物理学两⼤主要学科的合并：即随机过程的概率统计理论（⽤于处理布朗运动或随机游动实验）和位势理论，主要是研究均匀介质的稳定状态[1]。

它是⽤⼀系列随机数来近似解决问题的⼀种⽅法，是通过寻找⼀个概率统计的相似体并⽤实验取样过程来获得该相似体的近似解的处理数学问题的⼀种⼿段。

运⽤该近似⽅法所获得的问题的解in spirit 更接近于物理实验结果，⽽不是经典数值计算结果。

普遍认为我们当前所应⽤的MC 技术，其发展约可追溯⾄1944年，尽管在早些时候仍有许多未解决的实例。

MCM 的发展归功于核武器早期⼯作期间Los Alamos （美国国家实验室中⼦散射研究中⼼）的⼀批科学家。

Los Alamos ⼩组的基础⼯作刺激了⼀次巨⼤的学科⽂化的迸发，并⿎励了MCM 在各种问题中的应⽤[2]-[4]。

“Monte Carlo ”的名称取⾃于Monaco （摩纳哥）内以赌博娱乐⽽闻名的⼀座城市。

Monte Carlo ⽅法的应⽤有两种途径：仿真和取样。

仿真是指提供实际随机现象的数学上的模仿的⽅法。

⼀个典型的例⼦就是对中⼦进⼊反应堆屏障的运动进⾏仿真，⽤随机游动来模仿中⼦的锯齿形路径。

取样是指通过研究少量的随机的⼦集来演绎⼤量元素的特性的⽅法。

例如，)(x f 在b x a <<上的平均值可以通过间歇性随机选取的有限个数的点的平均值来进⾏估计。

这就是数值积分的Monte Carlo ⽅法。

MCM 已被成功地⽤于求解微分⽅程和积分⽅程，求解本征值，矩阵转置，以及尤其⽤于计算多重积分。

任何本质上属随机组员的过程或系统的仿真都需要⼀种产⽣或获得随机数的⽅法。